3. Теория информации и ML. Прогноз19.11.2022 22:47

Часть 2 — Mutual Information

Понятие Mututal Information (MI) связано с задачей прогноза. Собственно, задачу прогноза можно рассматривать как задачу извлечения информации о сигнале из факторов. Какая-то часть информации о сигнале содержится в факторах. И если вы напишите функцию, которая по факторам вычисляет число близкое к сигналу, то это и будет демонстрацией того, что вы смогли извлечь MI между сигналом и факторами.

Что такое Machine Learning?

Чтобы двигаться дальше, нам нужны базовые понятия из ML, такие как: факторы, target, Loss-функция, обучающий и тестовый пулы, overfitting и underfitting и их варианты, регуляризация, разные виды утечки данных.

Факторы (features) — это то, что вам даётся на вход, а сигнал (target) — это то, что нужно спрогнозировать, используя факторы. Например, вам нужно спрогнозировать температуру завтра в 12:00 в определённом городе — это target, а дано вам множество чисел про сегодня и предыдущие дни: температура, давление, влажность, направление и сила ветра в этом и соседних городах в разное время дня — это факторы.

Обучающие Данные — это множество примеров (aka сэмплов) с известными правильными ответами, то есть строчки в таблице, в которой есть и поля с факторами features=(f1, f2, …, fn), и поле target. Данные принято делить на две части — обучающий пул (train set) и тестовый пул (test set). Выглядит это примерно так.

Обучающий пул:

Тестовый пул:

В общих чертах задачу прогноза можно сформулировать в духе соревнования на kaggle.com:

Задача прогноза (задача ML). Вам дан обучающий пул. Реализуйте в виде кода функцию , которая по заданным факторам возвращает значение, максимально близкое к target. Мера близости задана с помощью Loss-функции, и значение этой функции называется ошибкой прогноза:
Качество прогноза определяется средним значением ошибки во время применения этого прогноза в жизни, но по факту для оценки этой средней ошибки будет использоваться некоторый тестовый пул, который от вас скрыт.

У величины есть специальное название — невязка. Два популярных варианта Loss-функции для задач прогноза вещественной величины — это:

• средний квадрат невязки, что также называют среднеквадратической ошибкой или mse (mean square error);

• средний модуль невязки, что также называют L1-ошибкой.

На практике задача ML более общая и высокоуровневая. А именно, нужно разработать в меру универсальную ML-модель — способ получения функций по данному обучающему пулу и заданной Loss-функции. А также нужно уметь делать model evaluation: мониторить качество прогноза в работающей системе, уметь обновлять обученные модели (пошагово, делая новые версии, или модифицируя внутренние веса модели в режиме online), улучшать качество модели, контролировать чистоту и качество факторов.

Процесс получения функции по обучающему пулу называется обучением. Популярны такие варианты ML-моделей (классы моделей):

• Линейная модель, в которой , и процесс обучения сводится к подбору параметров , что делается обычно методом градиентного спуска.

• Gradient boosted trees (GBT) — модель, в которой функция выглядит как сумма нескольких слагаемых (сотен, тысяч), где каждое слагаемое — это решающее дерево, в узлах которого находятся условия на факторы, а в листьях — конкретные числа; каждое слагаемое можно представлять как какую-то систему вложенных if-конструкций с условиями на значения факторов, где в конечных узлах находятся просто числа. GBT — это не только про то, что решение есть сумма деревьев, но и вполне конкретный алгоритм получения этих слагаемых. Для обучения GBT есть много готовых программ: CatBoost, xgboost. См. статью на хабре.

• Neural Networks — в простейшем базовом варианте это модель вида , где — матрицы, размеры которых определяет разработчик модели, факторы представлены в виде вектора , оператор соответствует умножению вектора на матрицу с последующим обнулением всех отрицательных чисел в результирующем векторе. Операторы выполняются в порядке справа налево — это важно в случае наличия такого обнуления. Матрицы называются слоями нейросети, а количество матриц — глубиной нейросети. Вместо обнуления отрицательных можно брать произвольные другие нелинейные преобразования. Если бы не было нелинейных преобразований после умножения вектора на матрицу, все матрицы можно было бы «схлопнуть» в одну и пространство возможных функций не отличалось бы того, что задаётся линейной моделью. Я описал линейную архитектуру нейросети, но возможны и более сложные, например,

  .

  Кроме самых разных поэлементных нелинейных преобразования и умножения на матрицу в нейросетях могут использоваться операторы скалярного произведения векторов и оператор поэлементного максимума для двух векторов одной размерности, объединения векторов в один более длинный и др. Можно думать об общей архитектуре для функции , когда на вход поступает вектор, а дальше с помощью операторов , нелинейных функций и весов конструируется ответ. В этом смысле нейросети могут представлять самой функции довольно общего вида. По факту, архитектуру функции называют нейросетью тогда, когда в ней присутствует что-то похожее на цепочку вида . А так, мы по сути имеем задачу регрессии — подобрать параметры (веса) в параметрически заданной функции, чтобы минимизировать ошибку. Есть множество методов обучения нейросетей, они в своем большинстве итерационные, и за шаг изменения весов отвечает модуль, который программисты называют оптимизатором, см. например AdamOptimizer.

Терминология ML

В регрессионном анализе появилось много важных терминов, которые позволяют лучше понять содержание задачи прогноза и не делать типичных ошибок. Эти термины практически без изменений перекочевали в ML. Здесь я изложу базовые понятия, стараясь отмечать связи с теорией информации

Overfitting

Overfitting (переобучение) — это когда выбранная вами модель сложнее, чем реальность, стоящая за target И/ИЛИ данных слишком мало, чтобы позволить себе обучать такую сложную модель. Есть две основные причины overfitting:

• too complex model: Устройство модели сильно сложнее, чем реальность или в своей сложности ей не соответствует. Проще это визуализировать на примере однофакторной модели.
  Пусть в обучающем пуле 11 точек , а модель — суть многочлен 10-й степени. Можно подобрать такие коэффициенты в многочлене, что он «заглянет» в каждую точку обучающего пула, но при этом не будет обладать хорошим качеством прогноза:

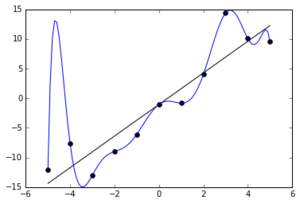  Голубая линия — многочлен 10 степени, который смог в точности воспроизвести обучающий пул из 11 точек. Но правильная модель скорее линейная (чёрная линия), а отклонения от неё — это или шум, или что-то, объясняемое факторами, которых у нас нет

  Многочлен 10-й степени — это очевидный и часто используемый пример переобучения. Многочлены невысокой степени, но от многих переменных тоже могут давать overfitting. Например, вы можете подбирать модель predict = многочлен степени 3 от 100 факторов (кстати, сколько в нём коэффициентов?), в то время как реальность соответствует predict = многочлен степени 2 от факторов + случайный шум. При этом, если у вас данных довольно много, то классические методы регрессии могут дать приемлемый результат и коэффициенты при членах степени 3 будут очень маленькими. Эти члены степени 3 будут вносить маленький вклад в ответ при прогнозе для типичных значений факторов (как в случае с интерполяцией). Но в зоне крайних значений факторов, где прогноз уже скорее экстраполяция, а не интерполяция, высокие степени будут вносить заметный вклад и портить качество прогноза. Ну и, конечно, когда данных мало, шум может начать восприниматься за чистую монету, и прогноз будет сложными поверхностями третьей степени стараться заглянуть в каждую точку обучающего пула.

• insufficient train data: Модель может более менее соответствовать реальности, но при этом вы можете не иметь достаточное количество обучающих данных. Приведём опять пример с многочленом: пусть и реальность и ваша модель есть многочлен 3-й степени от двух факторов. Этот многочлен задаётся 10 коэффициентами, то есть пространство возможных прогнозаторов у вас 10-мерное. Если в обучающем пуле у вас 9 примеров, то, записав равенство «многочлен (featuresi) = targeti» для каждого примера, вы получите 9 уравнений на эти коэффициенты, и их недостаточно, чтобы однозначно определить 10 коэффициентов. В пространстве возможных прогнозаторов вы получите прямую и каждая точка на этой прямой есть прогнозатор, который идеально повторяет то, что у вас в обучающем пуле. Вы можете случайно выбирать один из них, и это с высокой вероятностью будет плохой прогнозатор.

  • Важное замечание про обучение многопараметрических моделей. Пример выше может показаться искусственным, но правда в том, что современные нейросетевые модели могут содержать миллионы параметров или даже больше. Например, языковая модель GPT3 содержит 175 млрд. параметров.

    Если в вашей модели N = 175 млрд. параметров, а размер обучающего пула M = 1 млрд, то в общем случае вы имеете бесконечное множество моделей идеально подходящих под обучающий лог, и это множество — суть многообразие размерности N — M = 174 млрд.

    В случае с глубокими многопараметрическими нейросетями эффект »insufficient train data» проявляется в полный рост, если действовать неправильно. А именно, если искать строгий минимум ошибки на обучающем пуле, то получается плохой, overfitted, прогнозатор. Поэтому на практике так не делают. Выработаны интересные техники и интуиция про то, как обучать модель с N параметрами на M примерах, где M заметно меньше N. Используются регуляризационные добавки к Loss-функции (L2, L1), Stochastic Gradient Descent, Dropout Layers, Early Stopping, prunning и другие техники.
    ВАЖНО: Знание этих техник и умение их применять во многом и определяет экспертизу в ML.

Underfitting

Underfitting — это когда модель прогноза проще, чем реальность. Также как и в случае с overfitting здесь есть две основных причины:

• too simplistic model: выбрана слишком простая модель, сильно упрощающая то, что в реальности стоит за target. Такие случаи по-прежнему встречаются в продакшене, и обычно это линейные модели. Линейные модели привлекают своей простотой и наличием математических теорем, обосновывающих и описывающих их предиктивные способности. Но можно с уверенностью сказать, что если вы решите с помощью линейных моделей прогнозировать курс валют, погоду, вероятность покупки или вероятность возврата кредита, то вы получите слабую модель — under-fitted weak model.

• too early stopping: обычно процессы обучения моделей итеративны, и если проделать слишком мало итераций, то получается недообученная модель;

Data leakage

Data leakage — это когда вы во время обучения использовали то, что есть в тестовом пуле или данные, которые недоступны или отличаются от тех, что будут доступны на практике при применении модели в жизни. Модели, которые сумеют воспользоваться этой утечкой, будут иметь неоправданно низкую ошибку на тестовом пуле и выбраны для использования в жизни. Есть несколько видов data leakage:

• утечка таргета в факторы: Если, в задаче с прогнозом температуры вы добавите фактор — средняя температура за K дней, и в эти K дней при обучении случайно попадёт в том числе и целевой день, на который нужно сделать прогноз, то вы получите испорченный или нерабочий прогнозатор. Могут быть более сложные утечки через факторы. В случае прогноза какого-то будущего события вы должны многократно убедиться, что при вычислении факторов не используются данные, которые получены во время этого события или после.

• простая утечка тестового пула: Иногда всё просто — в обучающий пул попадают строчки из тестового пула.

• утечка через подбор гиперпараметров: Правило, что для обучения разрешено использовать только обучающий пул, обманчиво просто. Здесь можно легко обмануться. Типичный пример неявной утечки — это подбор гиперапараметров при обучении. У всякого алгоритма обучения есть гиперпараметры. Например, у градиентного спуска есть параметр «скорость обучения» и параметр, задающий критерий останова. Ещё вы к Loss-функции можете добавить регуляризационные компоненты и , и вот вам ещё два гиперапараметраи . Приставка «гипер» используется, чтобы отличать внутренние параметры модели (веса), от параметров влияющих на процесс обучения.
  Итак, предположим, вы решили в цикле проверять разные гиперпараметры обучения и выбрать те гиперпараметры, на которых достигается минимум ошибки на тестовом пуле. Надо понимать, что здесь происходит утечка тестового пула в модель. «Засаду», которая здесь скрывается, легко понять, именно с точки зрения теории информации. Когда вы задаете вопрос, чему равна ошибка на тестовом пуле, вы получаете информацию о тестовом пуле. А когда вы, на основании этой информации, принимаете какие-то решение, влияющие в конечном итоге на веса вашей модели, то значит биты этой информации оказываются в весах модели.
  Ещё можно проиллюстрировать концепцию утечки тестового пула доведя до абсурда понятие гиперапараметров. Ведь разница между весами (параметрами) и гиперпараметрами (параметрами процесса обучения) чисто формальная. Давайте веса модели, например коэффициенты многочлена 10 степени все назовоём гиперапараметрами, а процесса обучения у нас не будет (множество внутренних весов у нас будет пустым). И давайте запустим безумный цикл по перебору всех возможных комбинаций значений гиперпараметров (каждый параметр будем перебирать от -1000 до +1000 с шагом ) и вычислению ошибки на тестовом пуле. Понятно, что через условные миллиард лет мы найдём такую комбинацию параметров, которая даёт очень маленькую ошибку на тестовом пуле и картинку выше мы сможем запостить снова, но уже с другой подписью:

  Голубая линия — многочлен 10 степени, который смог в точности воспроизвести тестовый пул из 11 точек.

  Этот прогнозатор будет хорошо себя показывать на тестовом пуле, а в жизни — плохо.

  • На практике используются модели с тысячами или миллионами весов и описанные эффекты проявляются на пулах больших размеров, особенно при наличии утечки данных из будущего (см. ниже).

  • Надо понимать, что утечка теста через подбор гиперпараметров так или иначе всегда происходит. Даже если вы сделали специальный валидационный пул для подбора гиперпараметров, а тестовый пул никак не использовали для подбора гиперпараметров, всё равно наступает момент вычисления метрики качества на тестовом пуле. А потом наступает момент, когда у вас есть несколько моделей, измеренных на тестовом пуле и вы выбираете лучшую модель по метрике на тесте. Этот момент выбора также можно назвать утечкой, но не всегда нужно бояться этой утечки.

  • Важное замечание про то, когда нужно боятся этой утечки. Если эффективная сложность модели (см. определение ниже) у вас сотни или больше бит, то уже можно не боятся утечки такого сорта и не выделять специальный пул для подбора гиперпараметров (логарифм числа выстрелов для подбора гиперпараметров должен быть заметно меньше сложности модели).

  • утечка данных из будущего: например, когда вы обучаете прогнозаторы вероятности клика на рекламное объявление, то в идеале обучающий пул должен содержать данные, доступные исключительно на даты меньше даты X, где X — минимальная дата событий в тестовом пуле. Иначе возможны хитрые утечки типа следующей. Пусть мы взяли множества событий показы рекламы размеченной target = 1 для кликнутых событий показа, и target = 0 для некликнутой. И пусть мы разбили множество событий на тестовый и обучающий пул не по границе даты X, а случайным образом, например, в пропорции 50:50. Известно, что пользователи любят кликать сразу на несколько объявлений одной тематики подряд в течение нескольких минут, отбирая нужный товар или услугу. И тогда такие серии нескольких кликов будут случайно делиться на две части — одна пойдёт в обучающий, другая — в тестовый пул. Можно искусственным образом сделать модель с утечкой: возьмём самую хорошую правильную модель без утечки и дополнительно запомним факты «пользователь U кликал на тематику T» из обучающего лога. Затем при использовании модели будем совсем ненамного повышать вероятность клика для случаев (U, T) из этого множества. Это улучшит модель с точки зрения ошибки на тестовом пуле, но ухудшит её с точки применения на практике на новых данных. Мы описали искусственную модель, но несложно представить естественный механизм такого запоминания пар (U, T) и завышения вероятности для них в нейросетях и других популярных алгоритмах ML. Наличие таких утечек из будущего усугубляет проблему утечки через гиперпараметры. На таком тестовом пуле с утечкой будут выигрывать модели перекрученные в сторону запоминания данных. Более общим образом эту проблему можно описать так: модель может переобучиться под test set, если MI между примером в train set и примером в test set больше, чем между примером в train set и реальным примером при использовании модели в жизни.

Задачи

Задача 3.1. Пусть реальность такова, что  где — случайное число из  Фактор сэмплируется из  Сколько в среднем нужно обучающих данных, чтобы, имея соответствующую реальности модель, получить оценки весов равные истинным с точностью до среднеквадратичной ошибки ? Считайте, что априорное распределение весов — это нормальное распределение Запишите ответ как функцию от , ,

Задача 3.2. Пусть реальность такова, что target есть многочлен 2-й степени от 10 факторов, при этом коэффициенты в многочлене — это числа разово сэмплированные из , а факторы — независимые случайные числа из . Сколько нужно данных в обучающем логе, чтобы получить приемлемое качество прогноза, когда все факторы лежат на отрезке [-1, 1], для случая, когда модель верна, то есть многочлен 2-й степени?
А если модель есть многочлен 3-й степени?

Задача 3.3. Постройте модель пользователей, которые в каждый момент времени склонны больше кликать на объявления какой-то одной тематики, заинтересовавшей их в данный момент, и убедитесь, что деление пула на обучающий и тестовый пул не по времени, а случайно, приводит к утечке данных из будущего.
Можно взять, например, такую модель. У каждого пользователя есть 10 любимых тематик, мы их знаем и храним в профиле пользователя. Пользовательская активность разделена на сессии, каждая сессия длится 5 минут, и во время сессии каждый пользователь видит ровно 10 объявлений по одной из его 10 тематик, тематика из любимых выбирается случайно. В каждую сессию пользователь интересуется одной из этих 10 тематик особенно сильно, и нет никаких факторов, позволяющих угадать, какой именно. Вероятность клика для такой «горячей» тематики в 2 раза больше, чем обычно. Для каждого пользователя по истории его кликов мы хорошо знаем вероятности клика для его 10 тематик, и пусть, если их упорядочить по интересности для конкретного пользователя, вектор этих вероятностей равен {0.10, 0.11, 0.12, …, 0.19} .
Идентификатор пользователя и номер категории и есть доступные нам факторы. Насколько можно увеличить правдоподобие прогноза вероятности на тестовом пуле, если предположить, что каждая сессия разделилась ровно пополам между тестовым и обучающим пулами (5 событий пошли в один пул и 5 — во второй), и статистику по 5 событиям из обучающего пула можно использовать для прогноза вероятности клика на 5 других?
Предлагается экспериментально получить overfitting из-за утечки данных из будущего , используя какую-либо программу для ML, например, CatBoost.

Определение 3.1. Имплементационная-сложность функции (-ИС) — это то, сколько бит информации о функции нужно передать от одного программиста другому, чтобы тот смог её воспроизвести со среднеквадратичной ошибкой не более, чем . Два программиста предварительно договариваются о параметрическом семействе функций и априорном распределении параметров (весов) этого семейства.
Эффективная сложность модели — это минимальная имплементационная сложность функции среди всех возможных функций, которые дают такое же качество прогноза такое, что и данная модель.

Задача 3.4. Какая средняя -ИС функции вида

от n факторов, в которой веса сэмплированы из распределения , а факторы сэмплируются из .

Ответ

Задача 3.5. Функция t(id) задаётся таблицей как функция от одного фактора — id категории. Есть N = 1 млн. категорий, их доли в данных различны, и можно считать, что их доли получены сэмплированием 1 млн. чисел из экспоненциального распределения с последующей нормализацией, чтобы сумма долей была 1 (такое сэмплирование соответствует разовому сэмплированию из распределения Дирихле с параметрами {1,1,…,1} — 1 млн. единичек). Значения функции t для этих категорий сэмплированы из бета-распределения независимо от их доли.
Какова средняя-ИС таких функции?

Ответ

Задача 3.6. Пусть в предыдущей задаче смысл функции — вероятность клика на рекламное объявление. Перенумеруем все категории в порядке убывания их истинной доли и обозначим порядковый номер как order_id, а исходный случайный идентификатор как id. Предлагается рассмотреть разные варианты ML с огрублением номера (идентификатора) категории до натурального числа от 1 до 1000. Это ограничение может быть вязано связано, например, с тем, что вы хотите хранить статистику по историческим данным и у вас есть возможность хранить только 1000 пар (показы, клики). Варианты огрубления идентификатора категории:
(a) огрубленный идентификатор равный id' = id // 1000 (целочисленное деление на 1000);
(b) огрубленный идентификатор равный id' = order_id для топовых 999 категорий по доле, а всем остальным назначить идентификатор 1000;
© какой-то другой способ огрубления id' = G (id), где G — детерминированная функция, которую вы можете сконструировать на базе статистики кликов на 100 млн показов, где каждый показ имеет какую-то категорию с вероятностью ровной доле категорий, а клик происходит согласно вероятности клика для этой категории.
Оцените значение ошибки error в этих трёх вариантах, где а, а — это значение для идеального прогноза .

Задача 3.7. Пусть реальность такова, что , где — это шум, случайное число из . А ваша модель
где веса вам неизвестны и имеют априорное распределение лапласа со средним 0 и дисперсией 1. Последние 5 факторов модели по факту бесполезны для прогноза. Какого размера должен быть обучающий пул, чтобы получить среднеквадратическую ошибку прогноза

.

Сгенерируйте три пула №1, №2, №3 c размерами 50, 50, 100000 и узнайте как лучше действовать — (а), (б) или (в):
(а) соединить два пула в один и на основании объединенного пула найти наилучшие веса, минимизирующие на этом пуле
(б) для различных пар , найти наилучшие веса, минимизирующие на пуле №1; из всех пар выбрать такую пару , , на которых достигается минимум на пуле №2; пары предлагается взять из множества где и  геометрические прогрессии с  отдо 1. Нарисуйте график ошибки как функцию от , положив.
(в) соединить два пула в один и на основании объединенного пула найти наилучшие веса, минимизирующие на этом пуле; значения , взять из предыдущего случая.
Метод тем лучше, чем меньше ошибка на пуле №3, который соответствует применению модели в реальности. Стабилен ли победитель, когда вы генерируете новые пулы? Нарисуйте таблицу 3×3 mse ошибок на трёх пулах в этих трёх методах.
Как п

© Habrahabr.ru