[recovery mode] Решаем загадку круглых чисел на графике выборов 2018
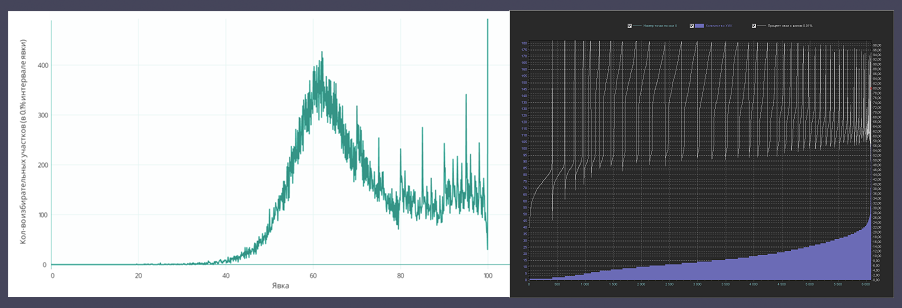
Данная статья является ответом на вот эту статью (Анализ результатов президентских выборов 2018 года. На федеральном и региональном уровне).
В той статье меня удивила фраза автора:
Вместо нормального или логнормального распределения мы видим интересную кривую, с очень странными пиками на круглых значениях (70%, 75%, 80% и т.д.), возрастающую на около-100% явке и уходящей далеко вверх на 100%.
Сразу возникают вопросы:
Почему автор считает, что вместо «странных» пиков должно быть нормальное или логнормальное распределение?
Почему вообще пики считаются «странными»?
Откуда могут появиться «естественные» пики на круглых значениях?
Та статья сильно политизирована и комментарии в ней соответствующие. В этой статье мы будем обсуждать только математику, поэтому политические взгляды попрошу держать при себе.
А в качестве бонуса, в конце статьи будет выложен ключ к решению загадки «круглых чисел» на графике выборов 2018.
Исходные данные
Файл БД (MongoDB) с результатами голосования (парсинг с гос. сайта), который был выложен автором исходной статьи:
Файл = 15–04–18.tar.xz
MD5 = 3a1c198cbc4ce102fbc074752fc0ca99
Мы будем исследовать график зависимости процента явки и количества УИКов с данной явкой. В исходной статье он выглядит так: 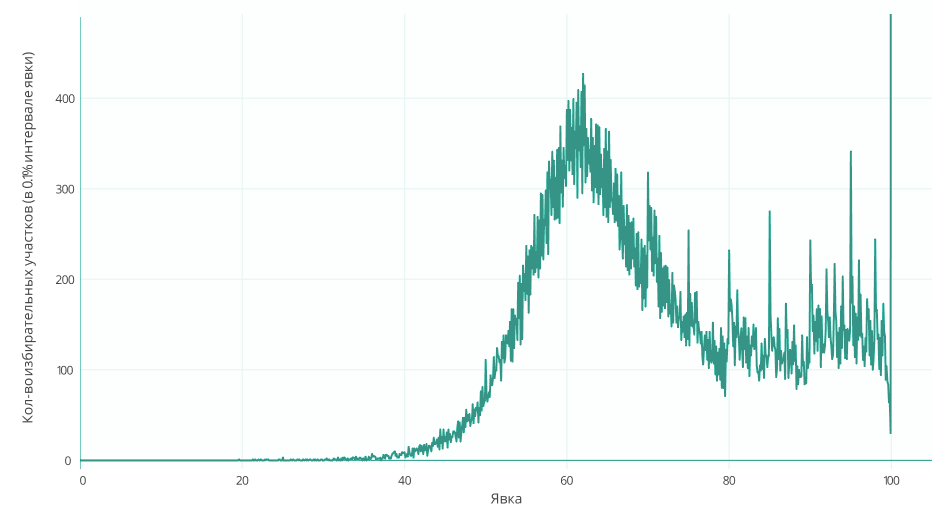
Вступление
Все желающие могут скачать БД и самостоятельно проверить на наличие ошибок. Мной из полученной БД были случайным образом выбраны и проверены данные по нескольким УИКам, что позволяет с некоторой вероятностью утверждать, что данные были загружены с гос. сайта корректно.
1. По какой формуле вы считали % явки на каждом уике?2. Поясните пожалуйста назначение атрибутов share и number_bulletin.
3. Каким образом округлялись значения до 0.1%?
Но, по структуре БД видно, что скорее всего, атрибут number_bulletin является самостоятельно рассчитанным параметром определяющим кол-во избирателей включаемых в «явку», а share — это процент явки, рассчитанный по формуле
share = number_bulletin / results_0;
где results_0 — это «Число избирателей, включенных в список избирателей».
На станицах гос. сайта атрибутов number_bulletin и share нет.
Странность заключается в том, что в БД number_bulletin не всегда считается корректно (с точки зрения официального расчета кол-ва людей принявших участие в выборах).
А именно, официальная формула такая:
Число бюллетеней, выданных на участке +
Число бюллетеней, выданных вне участка +
Число бюллетеней, выданных досрочно
В БД number_bulletin в большинстве случае совпадает с этой формулой, но при этом есть и множество УИКов, где number_bulletin отличается, от приведенной выше формулы на кол-во 1–2 и больше бюллетеней, причем закономерности я не увидел.
Вот выборка с примером и hash-ключами УИКов, чтоб можно было быстро найти в БД:
Порядок атрибутов в строке:
ID — ключ УИК
RESULTS_0 — поле results.0 из БД («Число избирателей, включенных в список избирателей»)
TEST_NUMBER_BULLETIN — рассчитанное значение по формуле
RESULTS_NUMBER_BULLETIN — значение в БД
TEST_YAVKA — рассчитанное значение по формуле
RESULTS_SHARE — значение в БД
5ab557a2866a6a69f2cf8c90 2241 1368 1367 0,610441 61
5ab557aa866a6a69f2cf8ca8 2853 1665 1662 0,583596 58,25
5ab557b1866a6a69f2cf8cba 2138 1413 1412 0,660898 66,04
5ab557b1866a6a69f2cf8cbb 2093 1291 1290 0,616817 61,63
5ab557b3866a6a69f2cf8cc2 2463 1688 1687 0,685343 68,49
5ab557b5866a6a69f2cf8cc7 1583 1085 1084 0,685407 68,48
5ab557b9866a6a69f2cf8cd7 1483 912 911 0,614969 61,43
5ab557ba866a6a69f2cf8cdb 2166 1403 1402 0,647737 64,73
5ab557bb866a6a69f2cf8cdd 2186 1204 1203 0,550777 55,03
5ab557bc866a6a69f2cf8ce1 1574 986 985 0,626429 62,58
5ab557bd866a6a69f2cf8ce5 1284 803 802 0,625389 62,46
5ab557bd866a6a69f2cf8ce6 2543 1610 1608 0,63311 63,23
5ab557bf866a6a69f2cf8ced 2215 1353 1350 0,610835 60,95
5ab557cf866a6a69f2cf8d36 1627 1374 1372 0,844499 84,33
5ab557f7866a6a69f2cf8dbd 449 262 261 0,583518 58,13
5ab557f8866a6a69f2cf8dbf 597 349 347 0,584589 58,12
5ab55809866a6a69f2cf8dfa 194 156 155 0,804123 79,9
Таким образом, если обсуждаемый график строился автором из БД с использованием значения share — то этот график не соответствует официальному варианту расчета явки. Но, я допускаю возможность, что данные атрибуты использовались автором в тестовых целях и приведенный им график построен без использования текущих значений share из БД.
В любом случае, все графики данной статьи строятся по официальным формулам и не используют вышеописанные атрибуты.
Официальная формула расчета явки:
Число бюллетеней, выданных на участке +
Число бюллетеней, выданных вне участка +
Число бюллетеней, выданных досрочно
Все графики в данной статье построены по следующим параметрам:
Явка на каждом уике = формула приведенная выше
Округление до ближайшего целого:
10.2 => 10
10.5 => 11
Округление до первого знака после запятой и последующих…:
0.22 => 0.2
0.25 => 0.3
Визуализация #1
Давайте посмотрим на графики с визуализацией кол-ва УИК по проценту явки, дополнительно добавив линию со средним размером УИК, чтобы проверить возможную корреляцию:
График_1а:
Ось Х — Процент явки (интервал = 1%)
Ось Y (левая) — Количество УИК
Ось Y (правая) — Средний размер одного УИК (кол-во зарег. избирателей)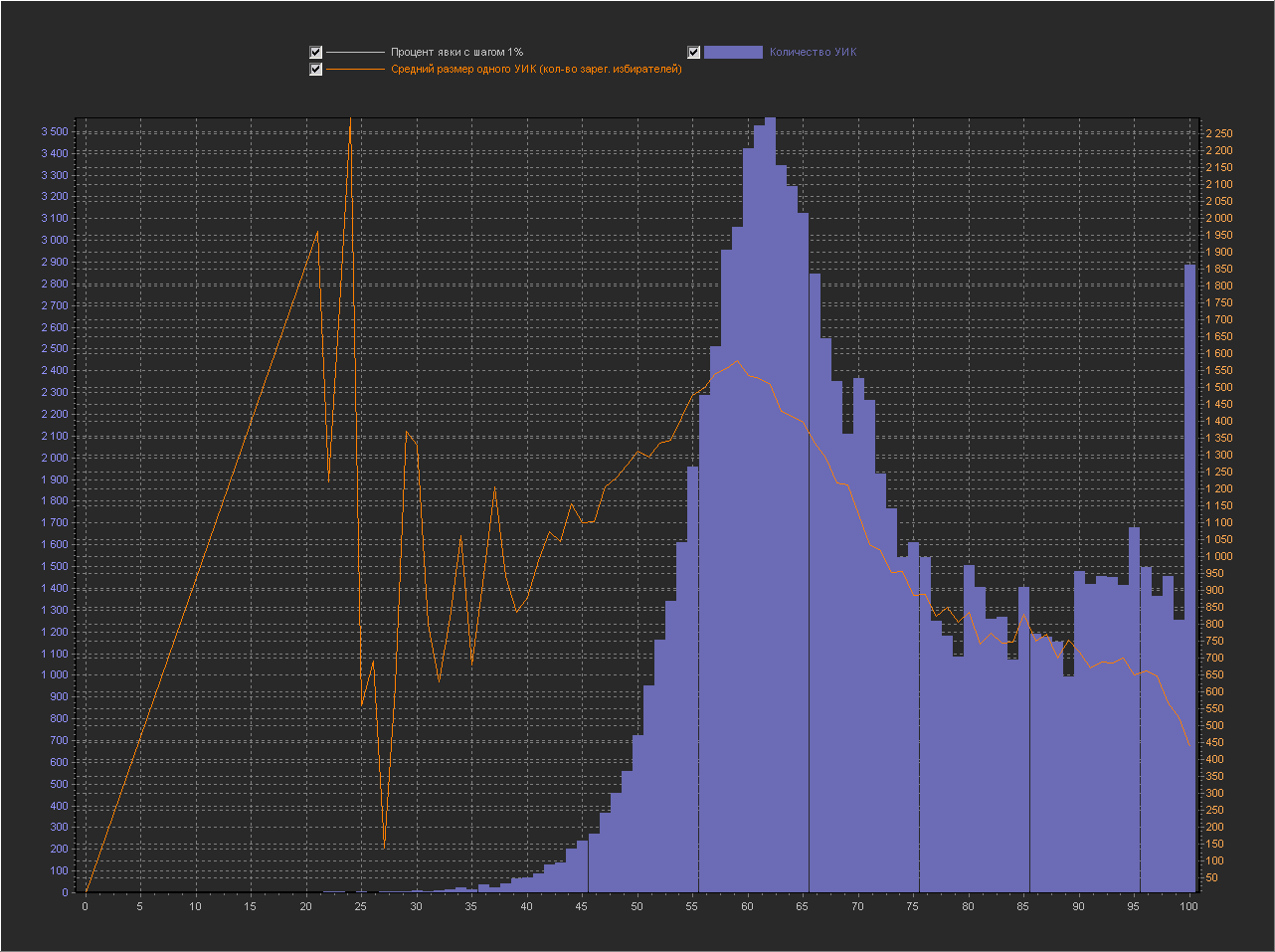
Видно, что на точке X=100 значение очень высокое, а средний размер УИК при этом уменьшается. В обсуждении fediq высказывалось логичное предположение:
Высокая явка — нормальное явление для высокоорганизованных УИКов типа традиционных общин, режимных учреждений, военных частей.
В качестве подтверждения, давайте посмотрим на первые 10 регионов по кол-ву УИК со 100% явкой:
K_ALL — кол-во УИК в регионе
K_100 — кол-во УИК со 100% явкой
REGION — название региона
K_ALL K_100 REGION
393 346 foreign-countries
1580 213 primorsk
1911 165 dagestan
482 156 sakhalin
596 138 murmansk
2817 132 tatarstan
2052 128 st-petersburg
317 123 kamchatka_krai
948 67 arkhangelsk
854 60 khabarovsk
График_1 б:
Ось Х — Процент явки (интервал = 0.1%)
Ось Y (левая) — Количество УИК
Ось Y (правая) — Средний размер одного УИК (кол-во зарег. избирателей)
+ Не выводится точка 100%, т.к. с ней остальные значения слишком мелкие.
Появились те самые пики на круглых значениях.
График_1в:
Ось Х — Процент явки (интервал = 0.01%)
Ось Y (левая) — Количество УИК
+ Не выводится точка 100%, т.к. с ней остальные значения слишком мелкие.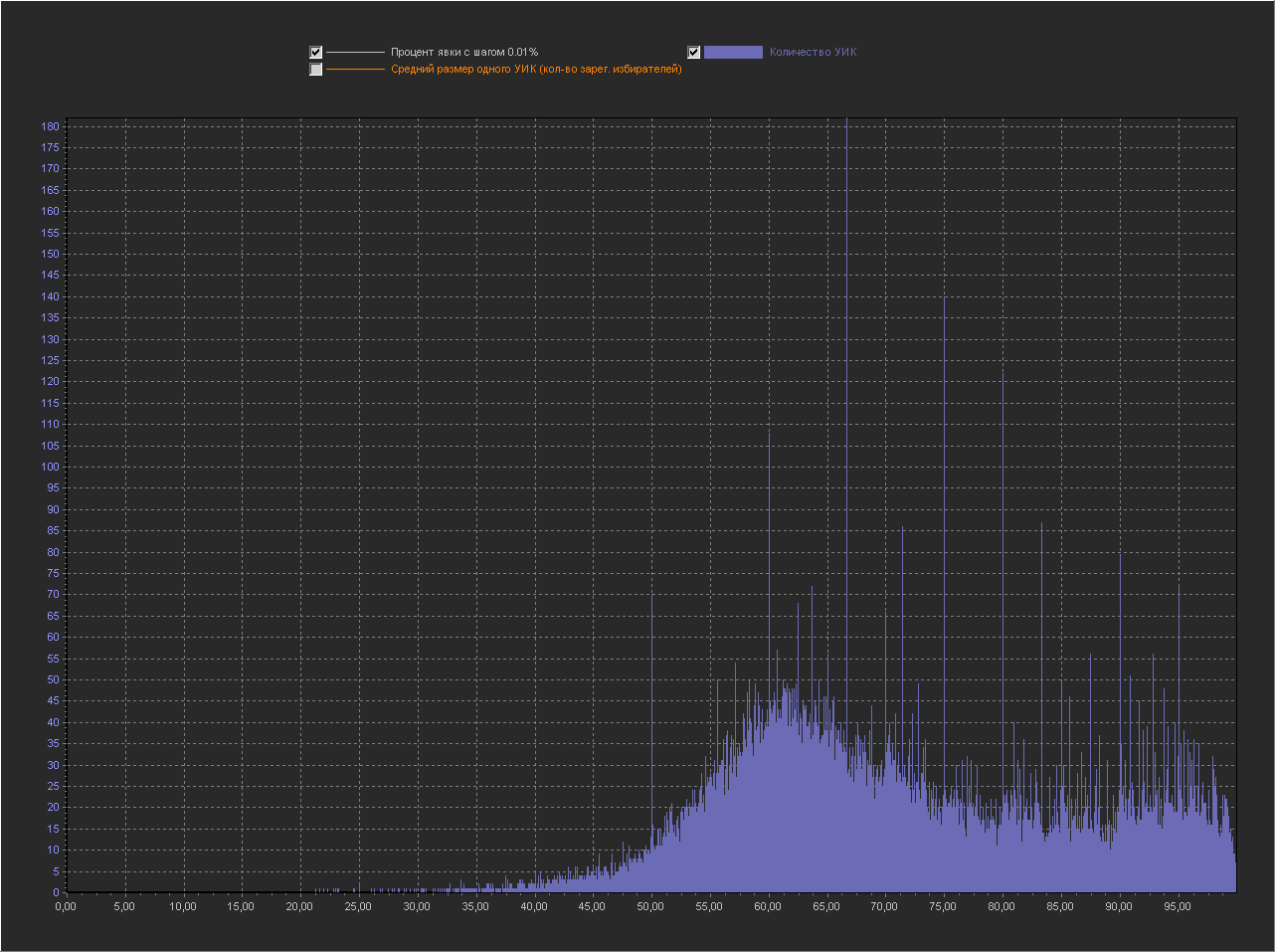
Как и ожидалось с уменьшением шага кол-во пиков увеличивается и они расположены по всему графику.
График_1 г:
Ось Х — Процент явки (интервал = 0.001%)
Ось Y (левая) — Количество УИК
+ Не выводится точка 100%, т.к. с ней остальные значения слишком мелкие.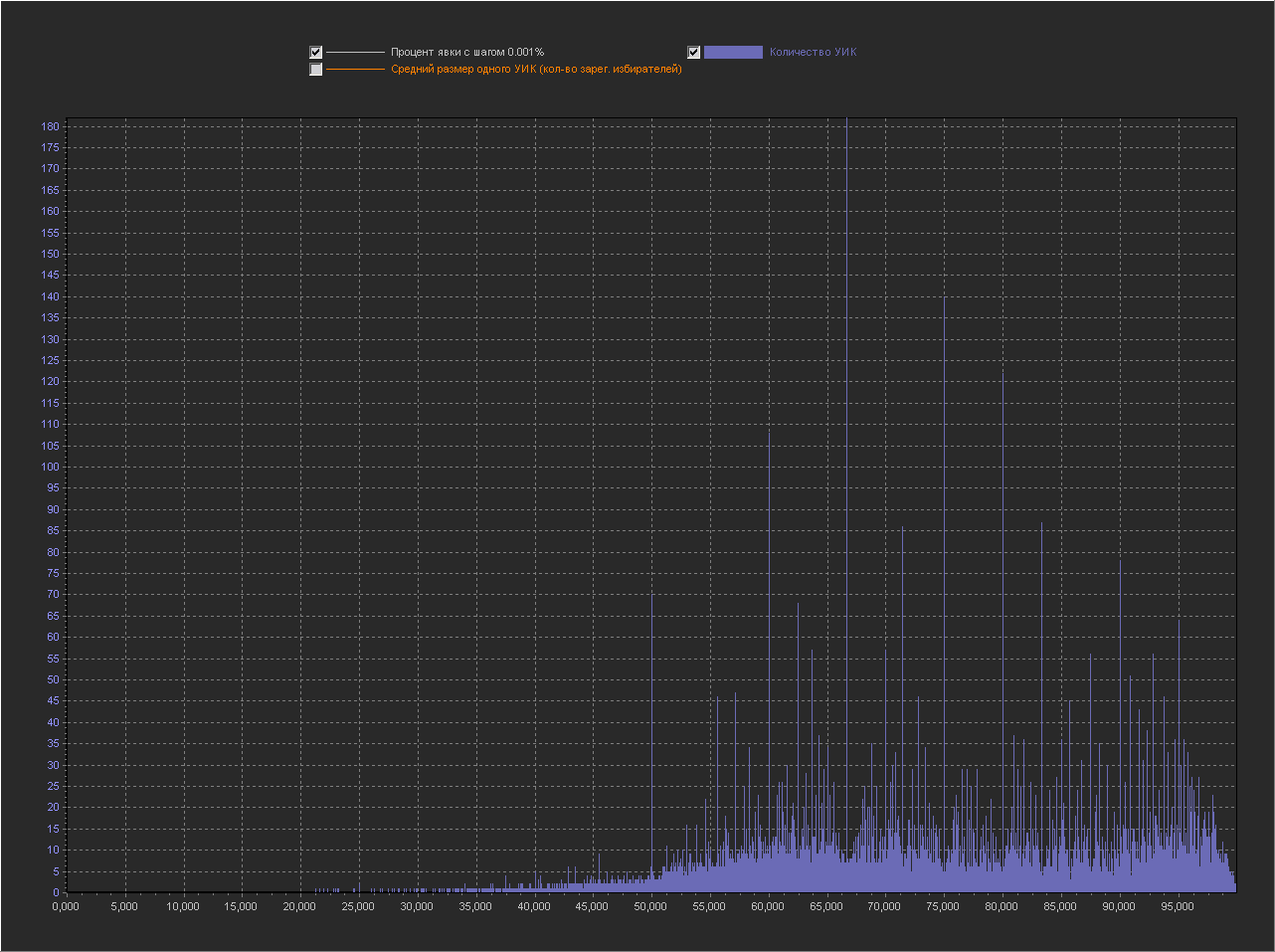
Как мы видим весь график в пиках, т.е. на данном масштабе — пики это нормальное явление.
График_1д:
Ось Х — Процент явки (интервал = 0.001%)
Ось Y (левая) — Количество УИК
Увеличенная область для значения 80%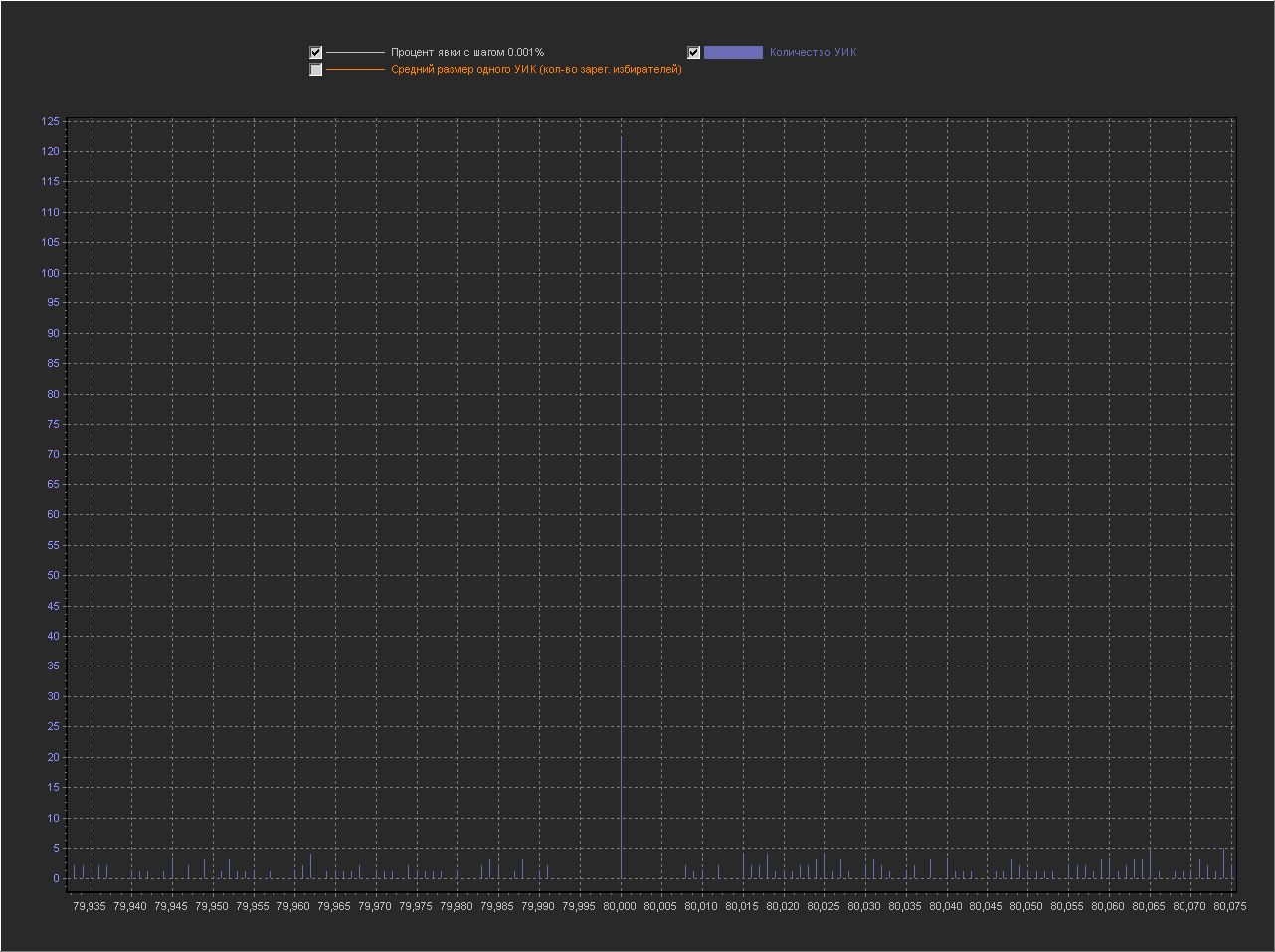
Видим, что рядом с круглым 80% много мелких значений.
Визуализация #2
Теперь давайте посмотрим на те же самые графики, но под другим углом. Так как расположенные рядом друг с другом на графике по оси X точки (процент явки) ни чем не связаны (в каждую такую точку-выборку попадают совершенно разные УИКи с различным гео-положением, размером и настроением избирателей и т.п…), то разницы в каком порядке они стоят нет, поэтому отсортируем их по оси Х не по возрастанию процента явки, а по возрастанию кол-ва УИКов.
Т.е. на графиках выше мы видели, как при возрастании процента явки ведет себя кол-во УИК, а на данном графике мы увидим, как при возрастании кол-ва УИК ведет себя процент явки.
График_2а:
Ось Х — номер точки из БД по порядку
Ось Y (левая) — Количество УИК
Ось Y (правая) — Процент явки (интервал = 1%)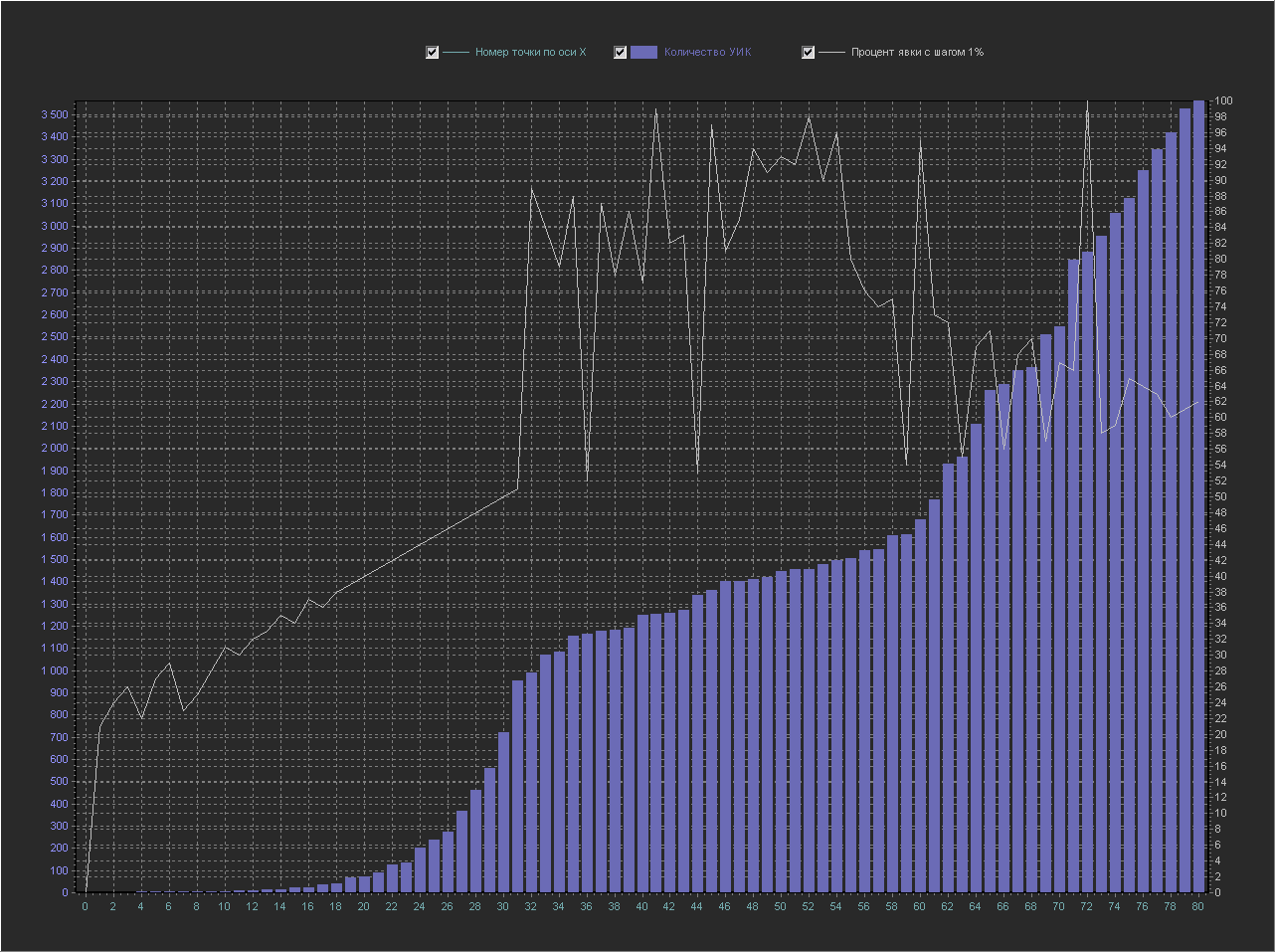
Это тот же самый график, который приведен выше, но ось X (белый цвет) теперь перенесена на Ось Y (правая) и отображается в виде отдельной линии, Ось Y (левая) так же как и раньше отображает кол-во УИК, а на оси X теперь отображается просто номер выборки из БД (номер точки по оси X по порядку).
Пояснение
Точке по оси X с номером 60 соответствует:
процент явки = 95
кол-во УИК = 1680
График_2 б:
Ось Х — номер точки из БД по порядку
Ось Y (левая) — Количество УИК
Ось Y (правая) — Процент явки (интервал = 0.1%)
+ Не выводится точка 100%, т.к. с ней остальные значения слишком мелкие.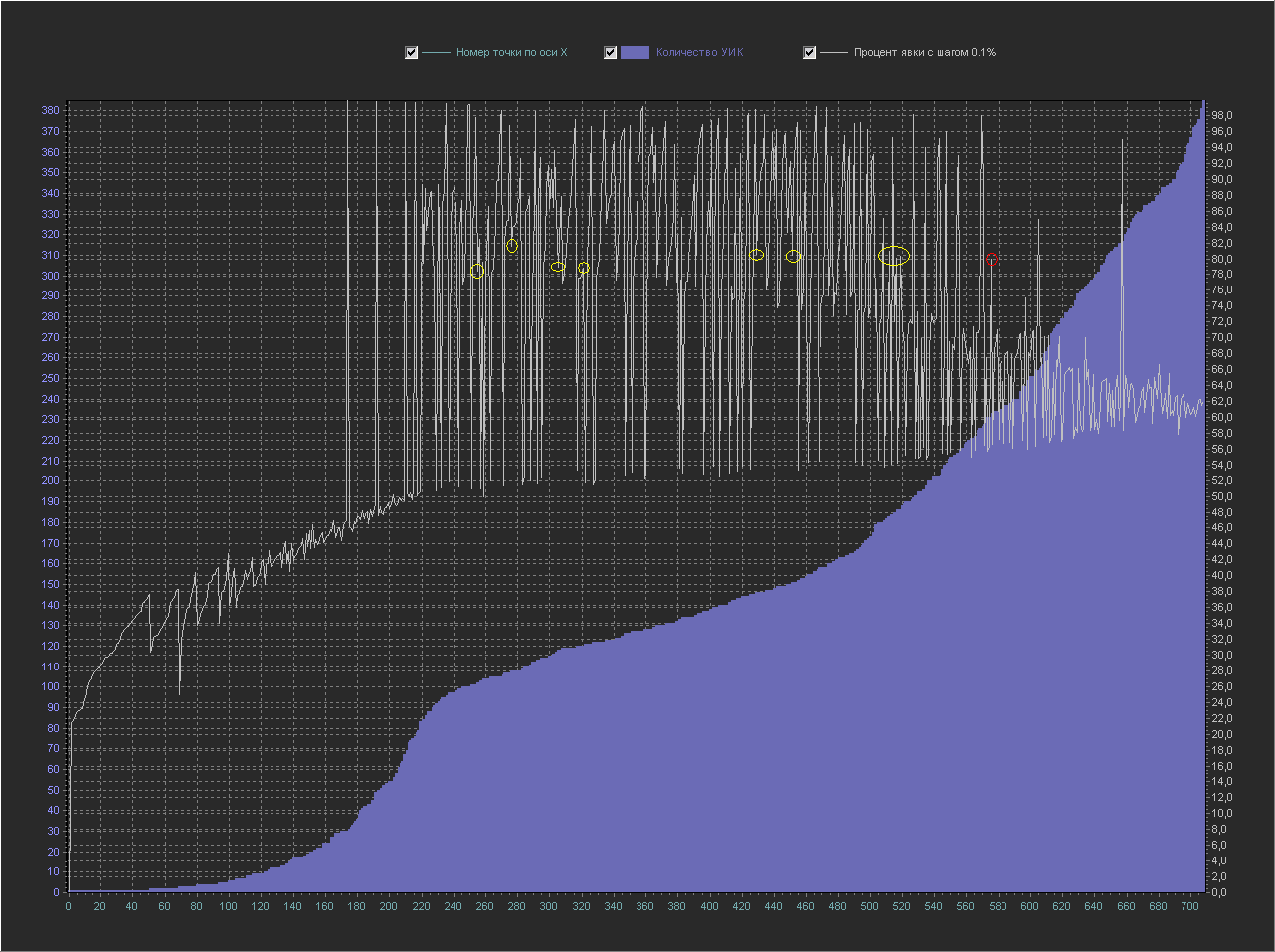
Давайте найдем на этом графике нашу круглую точку 80% (обведена красным кружком), которая на графике выше выглядела как пика с мелкими значениями вокруг себя.
Здесь она уже выглядит менее вычурно на линии с точками близкими ей по значению процента явки (желтые кружки).
График_2в:
Ось Х — номер точки из БД по порядку
Ось Y (левая) — Количество УИК
Ось Y (правая) — Процент явки (интервал = 0.01%)
+ Не выводится точка 100%, т.к. с ней остальные значения слишком мелкие.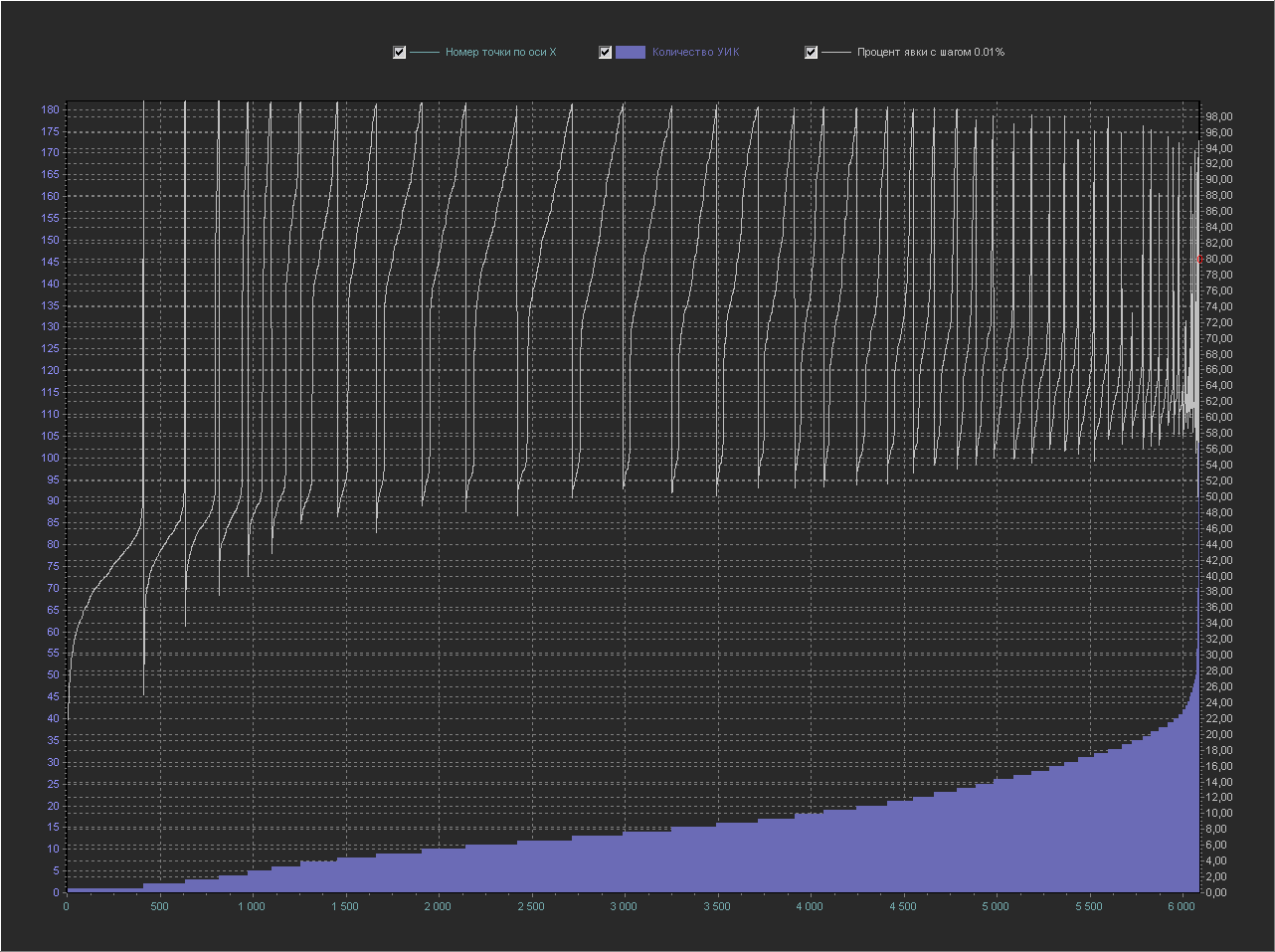
А вот это уже интересно, те, кто разбирается в математике уже наверно начинают понимать в чем фишка. А точку 80% уже не различить, т.к. на этом масштабе она уже не видна.
График_2 г:
Ось Х — номер точки из БД по порядку
Ось Y (левая) — Количество УИК
Ось Y (правая) — Процент явки (интервал = 0.001%)
+ Не выводится точка 100%, т.к. с ней остальные значения слишком мелкие.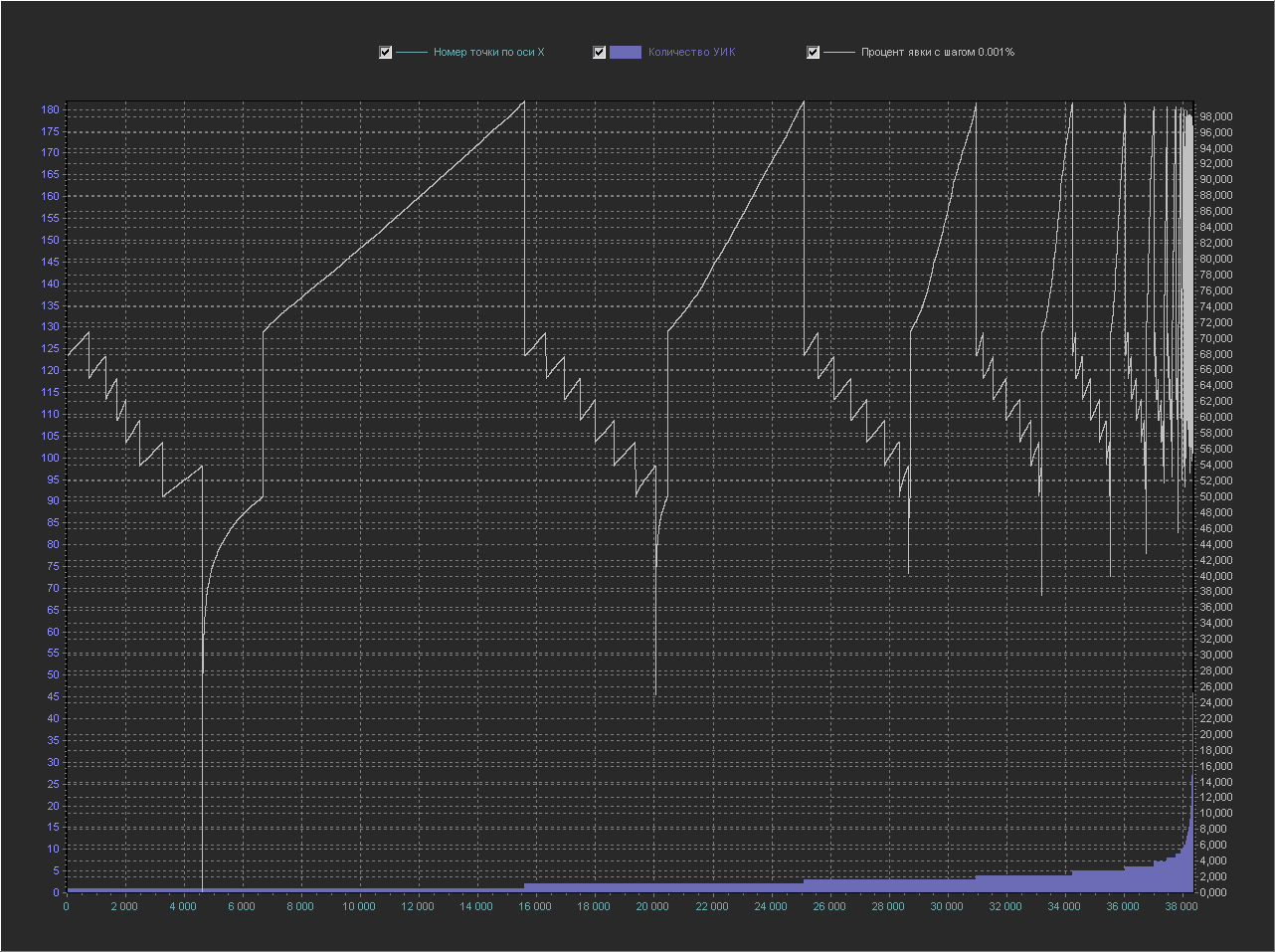
А этот график — просто откровение. Можно даже посчитать кол-во ступенек в каждом периоде…
Ключ к решению загадки круглых цифр
Ну и в качестве бонуса, любителям «конспиралогии» и математических ребусов посвящается:
PROCENTX KOLVO X2×5 X10
25 2 2 0 0
40 5 2 5 2
45 3 3 3 3
50 70 70 15 15
55 10 10 10 10
60 108 57 108 57
65 34 34 34 34
70 57 57 57 57
75 140 140 29 29
80 122 62 122 62
85 36 36 36 36
90 78 78 78 78
95 64 64 64 64
100 2613 1370 582 324
Это красивая закономерность, которую я обнаружил в «круглых цифрах».
Суть в том, что начиная с точки 40% и далее с шагом 5% количество УИК всегда кратно 2, 5 или 10. Собственно таблица выше это отображает.
PROCENTX — процент явки
KOLVO — общее кол-во УИК ровно с данным процентом без каких-либо округлений
X2 — количество УИК в которых кол-во зарег. избирателей кратно 2
X5 — количество УИК в которых кол-во зарег. избирателей кратно 5
X10 — количество УИК в которых кол-во зарег. избирателей кратно 10
Далее, я решил проверить кратность с шагом 1…
PROCENTX KOLVO X2×5 X10
25 2 2 0 0
34 1 1 1 1
36 1 1 1 1
40 5 2 5 2
42 1 1 1 1
44 2 0 2 0
45 3 3 3 3
46 1 1 1 1
47 1 1 1 1
48 2 0 2 0
50 70 70 15 15
51 3 3 3 3
52 7 4 7 4
53 4 4 4 4
54 4 4 4 4
55 10 10 10 10
56 10 6 10 6
57 5 5 5 5
58 9 9 9 9
59 4 4 4 4
60 108 57 108 57
61 3 3 3 3
62 18 18 18 18
63 1 1 1 1
64 23 10 23 10
65 34 34 34 34
66 14 14 14 14
67 8 8 8 8
68 22 10 22 10
69 2 2 2 2
70 57 57 57 57
71 4 4 4 4
72 17 5 17 5
73 6 6 6 6
74 8 8 8 8
75 140 140 29 29
76 23 11 23 11
77 4 4 4 4
78 10 10 10 10
79 2 2 2 2
80 122 62 122 62
81 10 10 10 10
82 14 14 14 14
83 6 6 6 6
84 24 11 24 11
85 36 36 36 36
86 10 10 10 10
87 3 3 3 3
88 23 8 23 8
89 4 4 4 4
90 78 78 78 78
91 4 4 4 4
92 31 17 31 17
93 6 6 6 6
94 13 13 13 13
95 64 64 64 64
96 25 11 25 11
97 6 6 6 6
98 17 17 17 17
99 4 4 4 4
100 2613 1370 582 324
Получается, что такая закономерность соблюдается кроме 100 на всех целых числах (в которых имеется ровно целое значение, если целого значения нет — оно в списке пропущено).
Ну и напоследок, общее разбиение по кратности количества зарегистрированных избирателей x2–10 для всех УИК:
KOLVO X2×3 X4×5 X6×7 X8×9 X10
97699 49413 32753 24724 20283 16649 13923 12464 10917 10411
KOLVO — общее кол-во УИК в которых проводились выборы
X2–10 — количество УИК в которых кол-во зарег. избирателей кратно 2–10
И общее разбиение по кратности пришедших на выборы избирателей x2–10 для всех УИК:
KOLVO X2×3 X4×5 X6×7 X8×9 X10
97699 49268 32712 24634 20608 16492 14085 12192 10938 10752
KOLVO — общее кол-во УИК в которых проводились выборы
X2–10 — количество УИК в которых кол-во пришедших избирателей кратно 2–10
Ну, а дальше обычно в таких случаях математики пишут… решение тривиально :)
