[recovery mode] Матстат и опоздания на работу

Привет, народ! В рамках курса Python для аналитики, хочу поделиться с вами небольшим шуточным исследованием, которое немного раскроет методику применения математической статистики и A/B тестирования в повседневной жизни. Данное исследование, как и статью в целом, подготовил мой коллега Роман Козлов.
В последнее время проблема с опозданиями не так уж остро стоит, ведь большинство работников, особенно в IT-сфере, работают на удалёнке. Однако, остались еще те последние из могикан, кто вынужден ходить на работу по старинке в офис.
Пересматривая этот момент из оригинальной Матрицы, после отвратительной четвертой части, я задумался, над таким явлением, как опоздание на работу. Неужели опоздание на работу не может быть случайным, независящим от работника фактором, чисто с математической точки зрения? Безусловно, с точки зрения работодателя, любое опоздание должно караться в соответствии с трудовым договором и распорядком учреждения. Однако, стоит ли быть столь категоричным?
Как известно, в 2022 году у граждан РФ будет 247 календарных трудовых дней. Возьмем для примера идеального аналитика ООО «Рога и Копыта» Василия, который работает без опозданий 247 из 247 дней в 2022 году (бедолага). Предположим, что в ООО «Рога и Копыта» существует еще некий разработчик Валера, который не столь пунктуален. Так сколько раз в году может опоздать на работу Валера, чтобы начальство не отругало?
Если свести эту задачу к математической статистике и A/B тестированию, то нам предстоит проверить утверждение: Отличается ли явка на работу аналитика Василия от явки разработчика Валеры? Если точнее, при какой явке Валеры на работу различие с Василием будет статистически значимым и различимым?
Поскольку опоздание на работу/приход вовремя на работу по сути представляет из себя биномиальное распределение и может принимать значение Истина/Ложь, то для проверки статистической гипотезы будем использовать критерий согласия Пирсона (Хи-квадрат).
Таким образом, мы будем сравнивать между собой двух работников: того, кто приходит на работу вовремя все 247 дней в году (аналитик Василий), и того, кто опаздывает (разработчик Валера). Тем самым, мы попытаемся найти порог того количества опозданий, после которого разница в этих группах станет статистически значимой и различимой, то есть эти опоздания будут свидетельствовать об их закономерности.
Функция, которая нам нужна, чтобы использовать хи-квадрат, есть в библиотеке statsmodels. Мы импортируем из нее объект stats.proportion, который позволяет считать пропорции.
Классический A/B тест (или эксперимент), который мы решим с помощью Python, будет выглядеть следующим образом. Мы обращаемся к методу proportions_chisquare, класса proportion. В качестве первого аргумента метод принимает целое число или массив, который указывает на количество «успехов» (в нашем случае это будет количество дней, когда Василий и Валера приходит на работу вовремя). Второй аргумент — это общее число наблюдений, то есть количество календарных рабочих дней в 2022 году.
import statsmodels.stats.proportion as proportion
chi2stat, pval, table = proportion.proportions_chisquare([244,247],247)
pvalКак вы видите, в первый аргумент мы просто «захардкодили» количества приходов вовремя на работу на Василия и Валеры — 244 и 247 дней соответственно, также как и общее количество наблюдений для нашего эксперимента — 247 календарных рабочих дней.
Метод proportions_chisquare возвращает сразу 3 переменные:
— chi2stat — это некая статистика, находящаяся под капотом нашего критерия (в данной задаче она нам не понадобится).
— pval — интересующее нас значение p-value.
— table — таблица сопряженности (также не понадобится).
Значение p-value, поможет оценить: есть ли статистическая значимость в разнице между группами работников, которые никогда не опаздывают на работу (Василий), и теми, кто приходит невовремя (Валера). Выбирая порог значимости a (альфа) равный 0.05, мы соглашаемся с тем, что 5% наших наблюдений будут ошибочными.
p-value — это фактическая вероятность попасть в ошибку первого рода на наших данных, если мы отклоним нулевую гипотезу. Нулевой гипотезой при этом будет считаться утверждение, что разница между пунктуальными и опаздывающими работниками является статистически значимой, то есть неслучайной. Соответственно, альтернативная гипотеза будет состоять в том, что эта разница не является значимой, то есть получена случайно
Давайте сравним p-value c желаемым уровнем точности нашего эксперимента.
— Если p-value меньше порога ошибки первого рода — результат эксперимента можно считать статистически значимым
— Если p-value больше — мы будем вынуждены признать разницу в явке пунктуальных и непунктуальных работников случайной
Мы получили значение p-value равное 0.08232820755666564, что больше общепринятого порога a = 0,05, а значит мы отвергаем гипотезу, что различие в явке статистически значимо. Значит 3 раза Валере опоздать, в целом, можно!
import statsmodels.stats.proportion as proportion
chi2stat, pval, table = proportion.proportions_chisquare([243,247],247)
pvalПредположив, что Валера опоздает 4 раза, мы получили p-value равное 0.04462770779632275. Это меньше a=0,05, так что опаздывать 4 раза Валере уже никак нельзя!
Тем не менее, в нашем эксперименте (как и в любом другом, связанном с A/B тестированием) не стоит забывать еще и о так называемой ошибке второго рода, или мощности проводимого эксперимента.
Мощность — это вероятность увидеть разницу там, где она существует. В нашем случае этот показатель укажет, можно ли было увидеть разницу в «пунктуальности» Василия и Валеры на временном промежутке в 247 календарных дней.
Общепринятым порогом для значения ошибки второго рода (мощности) является значение равное 0.8, то есть вероятности 80% того, что нашу разницу можно было увидеть.
Реализовать проверку мощности нашего эксперимента можно, импортировав из statsmodels объект stats.power, в котором есть нужные нам функции:

Присвоим переменной объект GofChisquarePower () из этой библиотеки, чтобы к нему было удобнее обращаться.
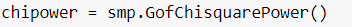
А затем нам нужно обратиться к методу solve_power (), в который необходимо передать как уже знакомые нам аргументы как nobs — количество наблюдений, alpha — порог ошибки первого рода, а также effect_size.
effect_size — это разница между относительными показателями пунктуальности Василия и Валеры. Эта разница вычисляется особым образом, формула выглядит так:

Используя формулу, найдем аргумент power, который и будет значением мощности эксперимента. Для этого присвоим ему значение None, значение nobs будет, по-прежнему, равно 247 дням, а alpha –значению p-value, вычисленному ранее для 4 опозданий Валеры.

Полученное значение мощности крайне мало! Оно означает, что вероятность различить разницу относительными показателями пунктуальности Василия и Валеры (effect size) на выборке в 247 календарных дней можно лишь с вероятностью примерно 5%. Таким образом, проходя по критерию значимости и удовлетворяя показателю ошибки первого рода, наш эксперимент не удовлетворяет ошибке второго рода.
Для того, чтобы эксперимент был успешен надо либо увеличить количество наблюдений, либо увеличить effect size, то есть увеличить количество дней опозданий для Валеры. Путем несложных вычислений, находим нужный показатель мощности на отметке в 206 дней опозданий для Валеры.

Таким образом, лишь опоздав на работу 41 день из 247 в году, можно утверждать, что разница в посещаемости Валеры по сравнению с Василием является статистически значимой и различимой.
Кстати, проделать эти и другие несложные манипуляции, связанные с A/B тестированием также можно в известном калькуляторе Эвана Миллера. Этот калькулятор позволяет не только сравнить значимость отклонений в двух выборках, но и ответить опытному исследователю и экспериментатору еще на ряд вопросов:
Сколько всего потребуется наблюдений для проведения A/B тестирования?
Какой процент «успеха» (конверсии) минимально необходим для проведения A/B тестирования?
Различаются ли средние значения в наблюдаемых группах?
Надеюсь, мои нехитрые размышления помогут в будущем всем тем, кому предстоит оправдываться перед руководством за опоздания! Не опаздывай, Валера!
