[recovery mode] Квантовая запутанность глазами хакера. Часть 1

Квантовая запутанность, изначально предсказанная в совместной работе Эйнштейна, Подольского и Розена, подразумевает взаимозависимость квантовых состояний двух или большего числа объектов. Такая взаимозависимость может сохраняться, даже если эти объекты разнесены в пространстве за пределы любых известных взаимодействий. Хотя Эйнштейн не рассматривал ЭПР-парадокс как описание какого-либо физического феномена, последующие эксперименты подтвердили существование запутанных состояний в реальном мире. Установлено, что корреляция запутанных пар происходит со скоростью, существенно превосходящий скорость света в вакууме. Вероятно, использование запутанных состояний позволило бы мгновенно передавать информацию на любые расстояния. Однако физики сходятся во мнении, что квантовая запутанность не может использоваться для передачи информации.
Квантовый мир словно использует надежную защиту, чтобы оставить в тайне свои секреты. Но любая защита — это лишь генератор ошибок перед правильным кодом. Как мы знаем, решением, казалось бы «невозможных задач» лучше всего справляются люди, обладающие нестандартным мышлением и творческим подходом. Поэтому, предлагаю рассмотреть способы решения данной задачи с точки зрения специалиста по информационной безопасности, вплотную опираясь на результаты реальных экспериментов. Каждый эксперимент шаг за шагом раскроет небольшие детали, которые позволят двигаться дальше в нужном направлении. Мы залезем в дебри квантовой механики и приоткроем завесу тайны, экспериментально показав «баги и фичи» не описанные в учебниках. В результате нам удастся провести ряд практических экспериментов во второй части данного поста, позволяющих получить уникальные результаты. Постараемся разобраться с алгоритмами квантового мира и подобрать правильные ключи к тайнам этого удивительного мира.
Гидра была основана на убеждении…
Физики убеждены, что квантовая запутанность не позволяет передавать какую-либо информации во многом благодаря так называемому No-communication theorem. Теорема предполагает, что Боб никак не сможет отличить начальное состояние σ от состояния P (σ) после измерения Алисой. Это доказывается математически, путем сравнения паттерна σ и паттерна P (σ). Тот факт, что паттерн никогда не меняется независимо от действий Алисы, является выводом теоремы об отсутствии связи. Означает ли это, что не существует других способов для построения квантовой коммуникации? Попробуем разобраться в этом вопросе.
ЭКСПЕРИМЕНТ С ОБРАТНЫМ ВОССТАНОВЛЕНИЕМ БАЗИСА
Рассмотрим для начала схему эксперимента, в котором возможно обратное восстановление начального квантового состояния:

Суть данного эксперимента состоит в следующем: на плечах интерферометра с помощью четвертьволновых пластин создаются разные направления круговой поляризации, которые после прохождения второго светоделителя позволяют получить разные направления линейной поляризации. На рисунке видно, как фотоны без каких либо потерь проходят через горизонтальный и вертикальный поляризатор, поскольку обладают соответствующей поляризацией. Предполагается, что если на вход интерферометра будут подаваться запутанные пары, и Алиса будет измерять поляризацию в той же оси, то на выходе первого интерферометра суперпозиция образоваться не должна. Например, если Алиса измерила запутанную пару и обнаружила, что фотон имеет горизонтальную поляризацию, то вторая пара должна иметь вертикальную поляризацию. Корреляция запутанных пар должно привести к тому, что на выходе интерферометра фотон должен будет находиться только на одном плече.
Что это дает? Если суперпозиция на выходе первого интерферометра как либо образом может быть нарушена, то это не позволит второму интерферометру восстановить первоначальное состояние фотона. Как видно из рисунка, второй интерферометр является зеркальным отражением первого, а значит, операторы эволюции производят обратное преобразование, восстанавливая первоначальный базис фотона. Но если измерение Алисы приведет к корреляции запутанных пар и нарушит суперпозицию между двумя интерферометрами, то никакого восстановления первоначального базиса не произойдет. На выходе из второго интерферометра фотоны должны будут направлены с 50% вероятностью вверх, и с 50% вероятностью вниз.
Очевидно, что такая схема работать не должна. Но в чем заключается ошибка, которая сводит на нет наши старания? Среди физиков существует ёмко выраженный афоризм «Заткнись и считай!», так что, рассмотрим для начала математические расчеты данной схемы. Допустим, что начальная поляризация фотона находится в горизонтальной плоскости.

Как видно из расчетов, на выходе первого интерферометра фотон действительно имеет суперпозицию двух направлений линейной поляризации, а на выходе второго интерферометра возвращается к первоначальной поляризации и первоначальному базису.

Математические расчеты в данном случае будут выглядеть следующим образом: 
Математические расчеты наглядно показывают что происходит с фотоном на каждом этапе эволюции, но не дают ответа на главный вопрос — на каком этапе происходит корреляция запутанных пар, и почему данная схема не работает? Чтобы это понять предлагаю проанализировать эксперимент квантового ластика, являющийся вариацией классического опыта Юнга на двух щелях. Полагаю, внимательный читатель обратит внимание, что в указанном эксперименте квантовое стирание нивелирует влияние круговых поляризаторов и приводит к восстановлению суперпозиции. Если мы вернемся и внимательно рассмотрим схему нашего эксперимента, то заметим следующее — четвертьволновые пластины на втором интерферометре являются теми самыми элементами, которые производят квантовое стирание линейной поляризации. Поскольку линейная поляризация подвергается квантовому стиранию, то никакой корреляций с запутанными парами в данном случае не происходит. Соответственно, суперпозиция на выходе первого интерферометра никоем образом не может быть нарушена, а восстановление первоначального базиса будет происходит всегда, независимо от действий Алисы. Поэтому, никакой сверхсветовой коммуникации в данном случае получить не удастся.
Данный эксперимент позволяет сделать важный вывод — наличие квантового стирания приводит к восстановлению суперпозиции. Значит, мы не должны допускать квантового стирания, либо необходимо обойти эти ограничения. В любом случае необходимо более детально разобраться с особенностями квантового ластика.
АНАЛИЗ ЭКСПЕРИМЕНТА КВАНТОВОГО ЛАСТИКА

Заменим круговую поляризацию на линейную, чтобы упростить наши расчеты. Несмотря на то, что теряются 50% фотонов на линейных поляризаторах, полученные результаты на выходе интерферометра будут идентичны использованию круговой поляризации.
Наша задача заключается в том, чтобы выяснить, какую поляризацию имеют фотоны на выходе интерферометра. Из представленного рисунка мы видим, что фотоны без потерь проходят поляризаторы, расположенные по оси (H+V) и (H—V). Означает ли это, что фотоны уже на выходе имеют поляризацию (H+V) и (H—V)? Ответом на этот вопрос будет — нет. Поляризация фотона на выходе интерферометра зависит от того, каким образом его измеряют. Если измерить по оси H и V, то можно будет узнать по какому плечу проходил каждый фотон. Но если измерить по оси (H+V) и (H—V) (как на представленной схеме), то все фотоны удивительным образом будут обладать поляризацией (H+V) или (H—V). Это является следствием квантового стирания — поскольку более невозможно узнать поляризацию фотонов на плечах интерферометра, то фотоны будут обладать суперпозицией, что позволит им пройти через оба плеча.
Допустим, что на вход интерферометра будут подаваться запутанные пары, и Алиса будет измерять свою часть запутанных пар по оси H и V. Означает ли это, что в представленной схеме можно восстановить информацию о том, через какое плечо интерферометра проходили фотоны? Ответ опять же — нет. Никакую информацию после принудительного квантового стирания восстановить не удастся. Соответственно, корреляции с запутанными парами на плечах интерферометра быть не может, а значит, измерение Алисы никак не влияет на поведение фотонов на выходе.
Квантовое стирание создает серьезные ограничения, которые сводят на нет любые попытки коммуникации с использованием запутанных пар. Но существуют ли способы обойти эти ограничения и построить квантовый ластик, позволяющий узнать через какое плечо интерферометра проходят фотоны?
КВАНТОВЫЙ ЛАСТИК С ВОЗМОЖНОСТЬЮ ВОССТАНОВЛЕНИЯ ИНФОРМАЦИИ
Вероятно некоторые скажут, что это в невозможно, но не спешите с выводами. Попробуем вначале задать себе вопрос — обязательно ли уничтожать информацию о состоянии фотона на плечах интерферометра, чтобы получить квантовое стирание?
Как показывают расчеты и проведенные мной эксперименты с нематическими жидкими кристаллами — это не обязательно. Можно просто развернуть поляризацию на одном плече интерферометра таким образом, чтобы она совпала с поляризацией на другом плече. В этом случае информация о поляризации фотонов становиться неопределенным, и возникает интерференция:
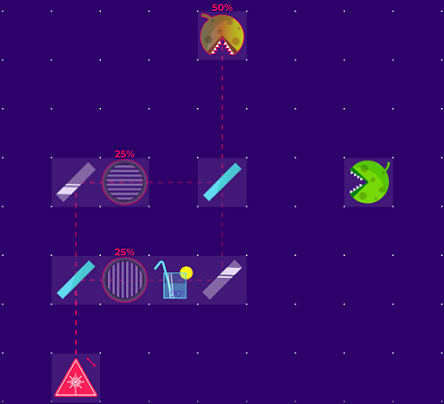
Мы меняем поляризацию фотона только на одном плече. А вторую не трогаем.
Что это дает? Это дает то, что информация о поляризации фотона оказывается неопределенным, если у фотона нет запутанной пары. При наличии запутанной пары информацию о том, через какое плечо интерферометра прошел фотон можно будет восстановить. Например, если Алиса измерила свою часть запутанной пары и обнаружила, что фотон имеет горизонтальную поляризацию, то вторая пара должна иметь вертикальную поляризацию. Как видно из схемы, фотон с вертикальной поляризацией в принципе не сможет пройти через верхнее плечо. Тоже самое, если Алиса обнаружит, что её запутанная пара имеет вертикальную поляризацию. Разворот плоскости поляризации на 90° не стирает информацию о начальной поляризации, а значит, вторая пара не сможет пройти через нижнее плечо. Поэтому, в обоих случаях будет известно через какое плечо интерферометра прошли фотоны. Суперпозиция на плечах будет нарушена, и на выходе интерферометра фотоны распределяться с 50% вероятностью вверх, и 50% вероятностью вниз.
Строго говоря, это не квантовый ластик в привычном понимании, поскольку мы не стираем информацию о том, какую поляризацию имели фотоны на плечах интерферометра. Мы лишь складываем ортогональные направления линейной поляризации таким образом, чтобы они оказались в одной плоскости, и в результате не было возможности узнать по какому плечу проходят фотоны (если у них нет запутанной пары). Именно в этом раскрывается удивительная особенность данного эксперимента — наличие интерференции на выходе подтверждает, что фотоны способны одновременно обладать как горизонтальной, так и вертикальной поляризацией, позволяя им проходить ортогонально направленные поляризаторы на обеих плечах интерферометра. Будто две альтернативные реальности складываются, образуя наш мир в виде интерференционного максимума, еще больше усложняя вопрос о том, кто или что может считаться наблюдателем. Ведь если фотоны запутаны с прибором, фиксирующим направление поляризации в каждой альтернативной реальности, быть может, мы наблюдаем интерференцию самого прибора…?
Но что, если Алиса будет проводить измерение по оси (H+V), (H—V)? Благодаря тому, что мы поворачиваем вертикальную поляризацию на 90°, на плечах интерферометра возникнет суперпозиция (H+H) и (H—H). Например, если Алиса измерила свою часть запутанной пары и обнаружила состояние (H+V), то на плечах интерферометра возникнет суперпозиция (H+H), соответственно, фотон на выходе будет направлен к верхнему детектору. А если Алиса обнаружила состояние (H—V), то на плечах интерферометра возникнет суперпозиция (H—H), значит, фотон на выходе будет направлен к нижнему детектору. В обоих случаях на выходе будет наблюдается интерференция, но в итоге, фотоны также распределятся с вероятностью 50% вверх, и 50% вниз.
Несмотря на то, что получили одинаковое распределение фотонов на выходе, данная схема квантового ластика является более перспективной. Предположим, что на входе интерферометра может быть только три возможных варианта поляризации: H, V и (H+V). Для состояний H и V мы получим распределение 50% на верхний детектор, и 50% на нижний детектор. А для состояния (H+V) мы получим интерференцию с 100% попаданием фотонов только на верхний детектор.
Остается лишь разделить запутанные пары таким образом, чтобы получить три возможных варианта поляризации не нарушая при этом состояния запутанности. Использование поляризационных светоделителей для этих целей не годиться. Попробуем использовать интерферометр с разным направлением линейной поляризации на плечах.
Из эксперимента квантового ластика мы узнали, что на выходе такого интерферометра состояние (H+V) будет направлено вверх, а состояние (H—V) будет направлено вниз. Состояния H и V в равной степени могут быть направлены либо вверх, либо вниз. А это то, что нужно для наших целей.
СХЕМА ЭКСПЕРИМЕНТА

Допустим, что на вход интерферометра будут подаваться запутанные пары, и Алиса будет измерять свою часть запутанных пар по оси (H+V), (H—V). В этом случае, на верхнем выходе первого интерферометра должно быть только одно значение поляризации — (H+V). Это приведет к возникновению на втором интерферометре суперпозиция (H+H), и на выходе фотоны со 100% вероятностью должны будут направлены только на верхний детектор. Результат должен соответствовать тому, что изображено на рисунке выше.
Но как поведут себя фотоны, если Алиса будет измерять запутанные пары по оси H и V?

Мы знаем, что на обеих интерферометрах можно определить по какому плечу проходили фотоны, если измерить поляризацию по оси H и V. Допустим Алиса измерила свою часть запутанной пары и обнаружила, что фотон имеет горизонтальную поляризацию. Соответственно, вторая пара должна иметь вертикальную поляризацию. Мы также знаем, что фотоны с вертикальной поляризацией в принципе не смогут пройти через верхнее плечо как на первом интерферометре, так и во втором. В итоге мы получаем отсутствие суперпозиции на обоих интерферометрах. Поэтому, на выходе второго интерферометра фотоны должны будут распределиться с 50% вероятностью вверх, и 50% вероятностью вниз.
Попробуем провести данный эксперимент на квантовом эмуляторе Quantum Flytrap используя нелинейный кристалл бета бората бария (BBO):

Полученные результаты, мягко говоря, не соответствует нашим ожиданиям. Почему же запутанные пары на квантовом эмуляторе ведут себя не так, как мы предполагали? Полагаю, пришло время для более детального анализа квантовых состояний.
АНАЛИЗ КВАНТОВЫХ СОСТОЯНИЙ
Допустим, что на входе интерферометра фотон имеет состояние (H+V). Рассмотрим математические расчеты для прохождения первого интерферометра: 
Сравним полученные данные с расчетами, если фотон будет иметь начальное состояние (H—V): 
Как видно, максимумы (H+V) и (H—V) на выходе интерферометра поменялись местами. Наши расчеты легко подтверждаются на квантовом эмуляторе:
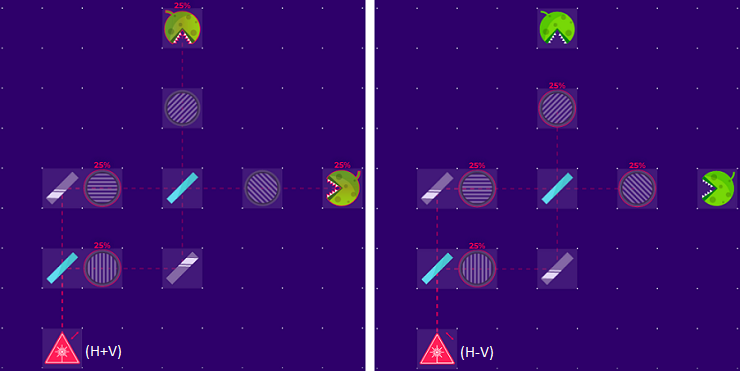
Какие выводы можно сделать из полученных данных?
Во первых, поляризация на выходе интерферометра меняется в зависимости от поляризации на входе. Поэтому, нельзя утверждать, что при использование запутанных пар состояние (H+V) будет направлено вверх, а состояние (H—V) направлено вниз. На каждом выходе интерферометра поляризация фотонов может быть как (H+V), так и (H—V), соответственно, никакой интерференции обнаружить не удастся. Удивительно, что даже авторитетные физики допускают ошибку в этом моменте, проводя аналогию с экспериментом квантового ластика. Использование линейной поляризации (или спина) оказывается не равнозначно использованию круговых поляризаторов как в эксперименте квантового ластика. Более подробную информацию об этом можно найти под спойлером.

Дело в том, что недостаточно просто создать разное направление круговой поляризации на плечах интерферометра. Нужно еще отсеять часть квантовых состояний, чтобы впоследствии можно было бы обнаружить интерференцию. Поэтому, в эксперименте квантового ластика применялись круговые поляризаторы — оптический элемент, состоящий из комбинации четвертьволновой пластины и линейного поляризатора. Линейный поляризатор в данном случае отсеивает часть квантовых состояний и позволяет на выходе интерферометра получить интерференцию.
Только в этом случае на выходе интерферометра возникает скрытая интерференция, когда Алиса производит квантовое стирании состояний запутанных пар. Вы можете убедиться в этом набирая на квантовом эмуляторе статистику состояний запутанных пар сопоставляя их с фотонами, попадающими на верхний и на нижний детектор. Схема эксперимента выглядит следующим образом:

На плечах интерферометра получается отнюдь не круговая поляризация, как можно подумать из описания квантового ластика, а линейная (подобное описание только больше вводит в заблуждение). Как и в нашем эксперименте, на плечах интерферометра возникает суперпозиция (H+H) или (H—H) которые на выходе будут направлены в разные стороны. Соответственно, путем сопоставления состояний запутанных пар можно обнаружить интерференцию.
Во вторых, если направление базиса на выходе совпадает с направлением базиса на входе, то фотоны будут иметь одинаковую поляризацию. Например, если начальный базис направлен вверх и фотоны имеют поляризацию (H+V), то на выходе с базисом вверх фотоны также будут иметь поляризацию (H+V). Для фотонов с поляризацией (H—V) ситуация будет аналогичной. В зависимости от того, какая поляризация зафиксирована на том или ином выходе интерферометра, всегда можно узнать какая поляризация была на входе. Из этого также следует, что эксперимент квантового ластика стирает информацию лишь о том, какая поляризация была на плечах интерферометра, но информация о начальной поляризации сохраняется. Соответственно, корреляций запутанных пар происходит с состоянием фотона на входе интерферометра, а состояние на выходе может быть совершенно разным (что, кстати, подтверждается на квантовом эмуляторе).
Становиться очевидным, что при таком раскладе рассмотренная схема эксперимента работать не будет, поскольку задача является более сложной, чем казалось на первый взгляд. Несмотря на это, нам удалось разобраться с квантовыми состояниями и сделать важные выводы, которые играют ключевую роль для понимания существующих ограничений. Далее рассмотрим другие, более изощрённые методы для решения данной задачи. Но обо всём этом уже во второй части данной статьи, где мы вплотную перейдем к практической части наших исследований.
