[Перевод - recovery mode ] История о дизайнере, покоряющем математику
Автор материала — дизайнер мобильных приложений. В своем посте он подробно описывает собственный путь в освоении математики, а также рассказывает о влиянии, которое точные науки оказали на его основную работу.

Я терпеть не мог математику
Математика меня раздражала. В юности мне казалось совершенно бессмысленным тратить столько времени на решение математических задач, когда вокруг было так много других интересных занятий!
На самом деле, если подучить математику, можно создавать прекрасные концепты!
Во время учебы в университете я записался на курс интерактивных искусств. Там меня показали, как творить с помощью кода в Processing. Вот один из примеров — восхитительная работа Мариуса Уотца (с тех пор я его поклонник).
Внимание! Содержит чрезмерную дозу великолепной удивительности.

Marius Watz2011
Будучи амбициозным студентом, я старался как можно лучше воспроизвести стиль, не стремясь вникать в неприятные мне вещи. Например, я не хотел разбираться в sin (что-то там) или cos (что-то там).

Кхе-кхе, двойная петля
Если честно, я был доволен своей работой. Она выглядела интересно, и я потратил на неё гораздо меньше времени, чем если бы делал то же самое в Illustrator или Photoshop. И все же я осознавал, что без понимания геометрии у меня не было шансов даже приблизиться к тому, что делал Мариус Уотц.
Из всех разделов математики больше всего я не любил тригонометрию. Но какая разница! Если с ее помощью можно создавать такие же крутые штуки, я готов продать душу, чтобы выучиться математике.
Я принялся учить математику снова

Рекомендую смотреть видео для старшеклассников.
Найти учебные материала оказалось на удивление легко. Они повсюду! Если вас усыпляет сонный голос одного ведущего и контент кажется слишком сложным для понимания, всегда есть тысячи альтернатив. Лично я смотрел YouTube-канал корейского учителя математики (просто я знаком с содержанием учебника и корейскими математическими нормами).
Не могу сказать, что я развлекся, но это помогло понять, что делал Мариус Уотц: когда он использовал косинус для позиции x и синус для позиции y.
Он просто помещал точку на круг!
Вместо чисел он пользовался тригонометрическими переменными, поэтому мог нарисовать точку, движущуюся по окружности!
Мои первые опыты в математике
Даже когда я понял основы тригонометрии, мне не хватало уверенности, чтобы применять их в дизайне. Я решил применить их на чём-нибудь ещё, пусть это даже выйдет смешным и не особо умным. С точки зрения эстетики получилось где-то в районе полной её противоположности.

http://share.framerjs.com/ejaybmwm4k95/
Я: ЛОЛ. Это так убого. *запостил в группе Framer в Facebook*
(Пару минут спустя)
Я: Что?! Людям нравится?!
(Пару часов спустя)
Я: Они думают, что я разбираюсь в математике. Вот это да!
В тот раз я понял: даже если делишься чем-то, что тебе самому кажется глупостью, это всё равно можно вдохновить окружающих, заставить их усмехнуться или улыбнуться. Так я получил мотивацию, чтобы создавать новые концепты и начать изучение фундаментальных областей геометрии.
Спиннер — отличный вариант для применения тригонометрии
Если не знаете, куда можно применить новые знания по тригонометрии — сделайте загрузочный спиннер (он же — круговой индикатор загрузки). Я использовал Framer для прототипирования.
Разработка анимаций для спиннера стала моим любимым занятием. Он в любом случае выглядит лучше простого вращающегося круга, при этом его не так уж сложно сделать. Нужно только подумать о трёх вещах:
- Сколько вершин будет у спиннера? (например, 3 вершины)
- Где на окружности будет располагаться каждая вершина? (например, каждые 120 градусов)
- Как вы хотите анимировать каждую вершину внутри цикла? (например, движение внутрь-наружу, сжатие-растяжение)

https://framer.cloud/ZePNP/

http://share.framerjs.com/e9f5sfvmrapa/
Всё что мне было нужно: эти три шага + знание основ тригонометрии. Вот так просто!
После изучения окружностей я перешёл к треугольникам
Для работы с треугольниками/звёздами/полигонами важен выбор инструментов. Бывают такие, где можно ввести две точки, и система соединит их линией.
В моём случае я не использовал Framer. Как вариант, я мог нарисовать прямоугольник и повернуть его так, чтобы он превратился в линию.

Сначала я практиковался в создании разных форм на базе треугольника.

https://framer.cloud/rJ68Ono4g/
Освоение математики приносит больше удовлетворения, когда ты накладываешь дополнительные ограничения!
А вот и я, полигоны!
К этому моменту я стал говорить, что люблю математику. Я изучал полигоны и создавал концепты в рождественские каникулы. Это самое захватывающее, что мне когда-либо приходилось изучать.
https://framer.cloud/H1fWocJSg/
Перед тем, как я узнал их получше, полигоны казались мне похожими на формочки для печенья. Я открывал Photoshop, Illustrator или Sketch и выбирал нужный инструмент для полигона. Я мог менять количество вершин от 5 до 12 — почти как выбирать разные формочки для печенья из ящика. Вот всё, что я знал о полигонах.

Скелет восьмиугольника
Узнав больше о полигонах, я понял, что это прекрасные структуры из треугольников, которые только и ждут, чтобы превратиться во что-то большее!
Работа с дугами
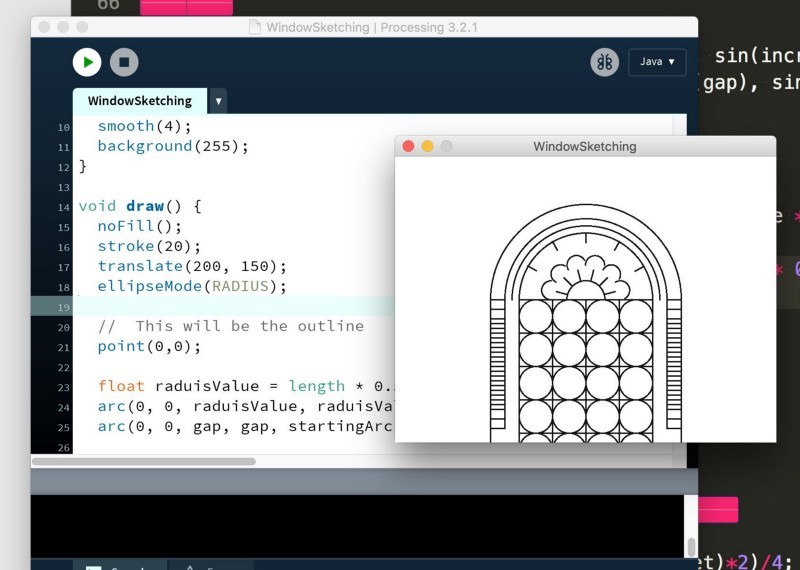
Как я уже сказал, есть инструменты, с помощью которых можно нарисовать линию от точки А до точки В. К счастью, это касается и Processing! А ещё в нём по-настоящему легко рисовать дуги. Это оживило мою креативную сторону в использовании математики.

Работа в процессе!

Скетчи
Несмотря на то, что Processing — слегка устаревший на сегодняшний день язык, у него есть отличное свойство — рисунок можно экспортировать в pdf-файл. А это значит, что можно добавить больше деталей в других программах, например, в Illustrator и Photoshop.

Цветная версия
Бонус — мои собственные фигуры
Разобравшись в тригонометрии, треугольниках и полигонах, можно нарисовать что угодно, сочетая их вместе.
И у вас может иногда не получаться, но это бывает даже забавно.

Талисман Олимпийских игр 1988
Есть еще один бонус от изучения геометрии — вы станете лучше понимать архитектуру.
Моя интерпретация архитектурного стиля района Гиндза в Токио
Смогу ли я использовать это в работе?
Ответ — да!
Если вы намереваетесь изучать что-то, что раньше ненавидели, убедитесь, что сможете применить новые знания в своей основной работе.
В моём случае (я занимаюсь дизайном мобильных приложений) я был удивлён, как много приложений, задействующих геометрию в дизайне UI! И вы можете легко поделиться своими знаниями с разработчиками, ведь большинство (или может все?) языки программирования в моей области поддерживают математические выражения.
Я продолжаю собирать примеры для этого кейса, поэтому ждите новых заметок:)
Если вам интересны мои маленькие открытия в математике — я по-прежнему изучаю что-то почти каждые выходные! Особенно, когда я немножко пьян, но только чуть-чуть.
Можете подписаться на меня в твиттере (@arle13) чтобы следить как я делаю небольшие смешные штуки.

