[Перевод - recovery mode ] Инверсная кинематика: простой и быстрый алгоритм
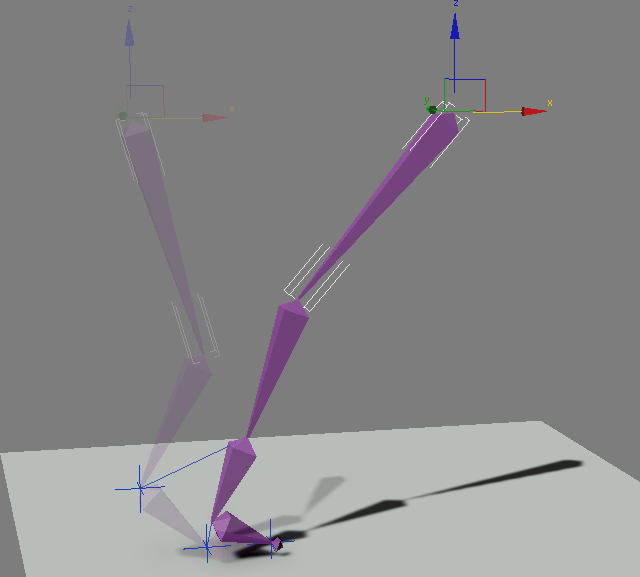Что такое «Инверсная кинематика»? Задачей инверсной кинематики является поиск такого набора конфигураций сочленений, который обеспечил бы максимально мягкое, быстрое и точное движение к заданным точкам. Однако, множество существующих ныне методов страдают от таких недостатков как высокая вычислительная сложность и неестественность результирующих поз. В этой статье описан новый (вероятно, на момент написания статьи — 2010 г.) эвристический метод под названием «Метод прямого и обратного следования» (Forward and Backward Reaching Inverse Kinematics, далее просто FABRIK), FABRIK избегает использования вращений и матриц в пользу непосредственного получения точки на прямой. Благораря этому, дело обходится всего несколькими итерациями, имеет низкую стоимость вычислений и визуально естественную позу в результате. FABRIK так-же без проблем справляется с наложением ограничений, а так-же использованием нескольких цепей и/или конечных точек. Именно об этом методе этот пост.
Прошу отнестись с пониманием к этой выжимке, потому-что оригинал довольно большой, имеет много воды, уместных и неуместных повторений и отстранений от темы, а так-же сравнений с другими алгоритмами. Этим я решил все-таки пренебречь, поэтому, тут содержится лишь малая часть текста, которая, однако, отражает суть — прим. перев.
1. Искусственная модель тела Система из множества твёрдых тел состоит из набора твёрдых тел, называемых узлами, соединёнными вместе рёбрами. Все рёбра являются компонентами concerned с движением: они ограничивают перемещения в пределах некоторого угла относительно соседних рёбер. Моделирование виртуального тела важно для вычисления позы человека. Модель с правильно расставленными ограничениями позволит получить набор правильных поз, что даст возможность получить более реалистичное движение. Большинство моделей подразумевают твёрдость частей тела, хотя это просто примерное приближение к реальности.Скелет обычно смоделирован в виде иерархии твёрдых сегментов соединённых рёбрами, каждое из которых задано такими свойствами как длинна, форма, обьём и масса. Манипулятор, на манер робо-руки или анимированного персонажа, смоделиован как цепь, собранная из твёрдых узлов, сопряженных друг с другом рёбрами. Каждое перемещение и/или вращение кости с индексом i влияет на все последующие элементы цепи. Цепь можно формализовать следующим образом: всякий узел без дочерних элементов следует величать конечной точкой; для каждой конечной точки цепь может быть сформирована движением обратно по скелету, от родителя к родителю до тех пор, пока не будет встречен корневой узел цепи (начало цепи). По определению, в задаче IK предполагается статичность корневого узла. Однако, методы обычно справляются с перемещением корня.Алгоритм полного цикла алгоритма FABRIK (псевдокод, первый элемент массива под индексом 1) Исходные данные: массив позиций узлов p[i] с i = 1…n, целевая позиция t и значения дистанций между сопряжёнными узлами. d[i] = | p[i+1] -t | for i = 1, … , n-1 Выходные данные: Новые позиции p[i], i = 1…n
//Дистанция между корнем и целью dist = | p[1] — t | //Проверяем достижимость цели
if dist > d[1] + d[2] + … + d[n-1] { //цель недостижима for i = 1, …, n-1 do { //Найдем дистанцию r[i] между целью t и узлом p[i] r[i] = | t — p[i] | lambda[i] = d[i] / r[i] //Находим новую позицию узла p[i] p[i+1] = (1 — lambda[i]) * p[i] + lambda[i] * t } } else { //Дель достижима; т.о. b будет новой позицией узла p[1] b = p[1] //Проверяем, не выше ли дистанция между конечным узлом p[n] и //целевой позицией t значения терпимости (tolerance) DIFa = | p[n] — t | while DIFa > tol do { //Этап 1: прямое следование //Устанавливаем конечный узел p[n] в качестве цели (вероятно, имелось ввиду «ставим на позицию цели» — прим. перев.) p[n] = t for i=n -1, …, 1 do { //Получаем расстояние r[i] между узлом p[i] и новой позицией p[i+1] r[i] = | p[i+1] — p[i] | lambda[i] = d[i] / r[i] //Вычисляем новую позицию узла p[i] p[i] = (1 — lambda[i]) * p[i+1] + lambda[i] * p[i] } //Этап 2: обратное следование //Устанавливаем корневому элементу p[1] начальную позицию p[i] = b for i=1,…, n — 1 do { //Получаем дистанцию r[i] между узлом p[i+1] и позицией p[i] r[i] = | p[i+1] — p[i] | lambda[i] = d[i] / r[i] //Получаем новую позицию p[i] p[i+1] = (1-lambda[i]) * p[i] + lambda[i] * p[i+1] } DIFa = | p[n] — t | } }
2.FABRIK — новое эвристическое решение задачи IK
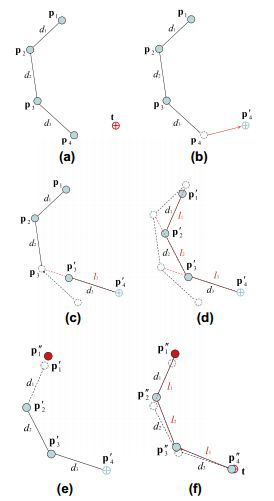В этой части предоставляется суть метода FABRIK. Он использует позиции, уже рассчитанные в режимах прямого и обратного следования. FABRIK достигает минимизации ошибки путём единоразовой подстройки угла каждого узла. Т.е. происходит обход всей цепи, начиная с последнего узла, с подстройкой угла каждого обойдённого узла, после чего, происходит обход цепи уже в обратном направлении. Этот метод, в отличие от преобразования вращений, обращает задачу поиска позиции узла в задачу поиска точки на прямой; следовательно, можно сэкономить время и уменьшить количество вычислений. Предположим что множество p[1], …, p[n] является множеством позиций узлов манипулятора. Также, предположим что p[1] является корневым узлом и p[n] является конечным узлом, т.о. для простоты оставим один конечный узел. Цель представлена позицией t и начальной базовой позицией b. Метод FABRIK представлен в листинге выше и графической интерпретации полного цикла на рисунке слева, с одной целевой точкой и четырьмя узлами в цепи. Рассмотрим полный цикл алгоритма на рисунке: a — Начальные позиции манипулятора и цели.
b — Двигаем конечный узел p[4] к цели.
c — Обнаруживаем позицию p'[3], лежащую на линии между позициями p'[4] и p[3], на дистанции d[3] от точки p'[4].
d — Повторяем для всех узлов.
e — Вторая стадия алгоритма: передвигаем крневой элемент с позиции p'[1] на его начальную позицию.
f — Повторяем для всех узлов, но на этот раз начинаем с базы и двигаемся к конечному узлу. Алгоритм повторяется до тех пор, пока позиция конечного элемента не приблизится к цели на достаточное расстояние.
Более подробно: Сначала считаются позиции между узлами (массив d), после чего идёт проверка, достижима ли целевая точка; считается расстояние между корневым узлом и целью (dist), и если эта дистанция меньше общей суммы дистанций между узлами, то цель достижима, иначе нет. Если цель достижима, полный цикл ограничивается двумя этапами. На первом этапе, алгоритм оценивает начальную позицию каждого узла, начиная с конечного элемента p[n] двигаясь к базе манипулятора p[1]. Таким образом, позволим целевой позиции быть позицией конечного узла, p'[n] = t. Получим прямую l[n-1], лежащую на точках p[n-1] и p'[n]. Новая позиция узла с индексом n-1, p'[n-1], лежит на этой линии на дистанции d[n-1] от p'[n]. Аналогично, новая позиция узла с индексом n-2, p'[n-2], может быть вычислена используя прямую l[n-2], лежащую на точках p[n-2] и p'[n-1] на дистанции d[n-2] от p'[n-1]. Алгоритм повторяется до тех пор, пока все не будут посчитаны новые позиции для всех узлов, включая конечный. В случаях, когда корневой элемент перемещается на необходимую позицию, FABRIK срабатывает как было описано, тем лишь отличием, что новая позиция p''[1] корневого узла будет желаемой позицией, а не начальной.После одной полной итерации, почти во всех случаях (по наблюдениям) конечный узел приблизится к цели. Процедура повторется необходимое количество раз, до тех пор, пока конечный узел не ляжет на позицию цели или не приблизится к ней на допустимую дистанцию. Реализация метода FABRIK без введения ограничителей сойдётся на любой целевой точке/цепи, если цель достижима. Однако, если цель находится дальше достанции, на которую может вытянуться цепь, необходимо прерывающее условие, которое сравнит прошлую и текущую позицию конечного узла, и которое прекратит выполнение алгоритма если смещение конечного узла будет меньше некоторого значения (эпсилона). Так-же, в особых случаях, алгоритм прерывается по истечению некоторого числа итераций (впрочем, пока-что такая ситуация не была встречена).Для более быстрого результата и решения в несколько итераций, возможна оптимизация с применением Конформной Геометрической Алгебры (Conformal Geometric Algebra, далее CGA); CGA имеет преимущество на базовых фигурах, такие как сферы, прямые, плоскости и окружности, достаточно просто отображаемые алгебраическими обьектами. Поэтому, поиск позиции узла, находящегося между двумя известными узлами, может быть выражен пересечением двух сфер с центрами на соответствующих этим узлам позициям, и радиусом, равным расстоянию между позициям искомого узла и имеющимися; новая позиция узла будет лежать на ближайшей точке окружности, сформированной пересечением двух сфер. Другая простая оптимизация заключается в прямом построении прямой в направлении цели, когда последняя недоступна.
3. Модель с множеством конечных узлов
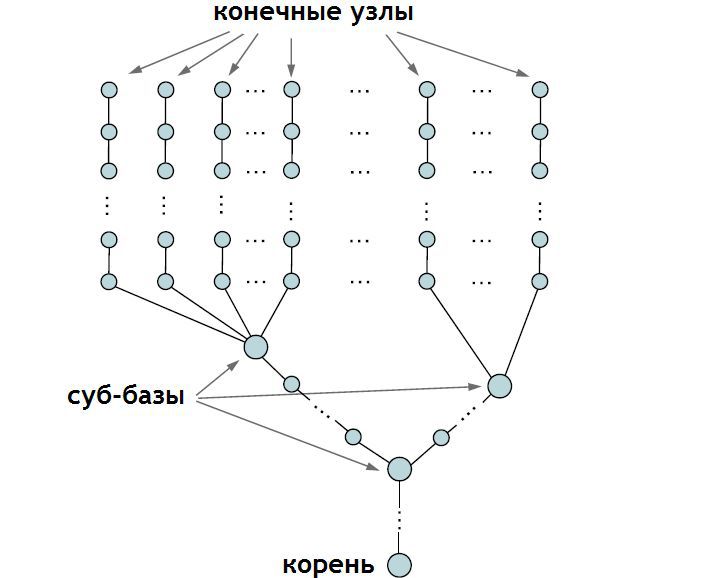Как и в случае с одним конечным узлом, алгоритм разбивается на два этапа: Первый этап точно такой-же, только на этот раз начинается от каждого конечного узла с движением внутрь по цепи от этого узла, вплоть до суб-базы (вероятно, суб-базой является узел с несколькими примыкающими к нему рёбрами — прим. перев.). Таким образом, получим столько разных позиций для суб-базы, сколько соединённых с ней конечных узлов у нас имеется. Итоговая же позиция может быть взята как центроид (тобиш, просто среднее арифметическое — прим. перев.) из этих позиций. После этого, выполнение алгоритма продолжается в нормальном режиме, двигаясь от суб-базы до корня. Если суб-базы имеют собственные суб-базы, то по отношению к ним производятся аналогичные действия — так-же составляется список возможных позиций, после чего эта суб-база устанавливается на центроид из всего списка позиций.
На втором этапе, обычный алгоритм применяется к каждому узлу, двигаясь всё дальше от корневого узла. При этом, каждая цепь должна быть обработана отдельно вплоть до конечного узла: чем больше суб-баз, тем больше повторений для каждой из них. Процесс повторяется до тех пор, пока конечные узлы не достигнут своей цели или пока не сработает условие прерывания.
4. Ограничители
Ну и наконец, самая вкусная часть этой статьи — рассчёты с применением ограничителей. Нужны они, как уже стоило догадаться, для большего сходства с реальными организмами. Сам же узел, обычно, характеризуется тремя степенями свободы. Вращение узла может быть характеризовано как «простое вращение» (2 степени свободы), которое отражает его конечную позицию, и вращение вокруг собственной оси (1 степень свободы). Таким образом, разделив передвижение узла на две такие фазы, и применив к ним ограничители, можно управлять положением узла. Сами же ограничения можно наложить подобным образом: т.к. алгоритм итеративный, можно применять ограничения вращений на каждой итерации алгоритма. Ограничители, при этом, не повлияют на сходимость алгоритма. Основная же идея применения ограничителей заключается в репозициионировании и переориентации узлов в пределах ограничений.
a — Начальные конфигурации манипулятора и цели.
b — Двигаем конечный узел p[4] к цели и ориентируем его на неё.
c — Обнаруживаем позицию p'[3], лежащую на линии между позициями p'[4] и p[3], на дистанции d[3] от точки p'[4].
d — Переориентируем узел на позиции p'[3] таким образом, чтобы он смотрел вдоль ребра, соединяющего p'[3] и p'[4].
e — Вычисление ограничивающего эллипса: разрешённые позиции находятся в затенённом участке. Ни одна из вершин на этом этапе никуда не двигается.
f — Узел p[2] перемещается на позицию p^[2], который является ближайшей позицией на затенённом эллипсе, удостоверяясь таким образом в том, что новая позиция p^[2] будет лежать в допустимых пределах.
g — Двигаем узел p^[2] на точку p'[2], чтобы сохранить длинну ребра.
h — Переориентируем p'[2], чтобы удовлетворить ограниение ориентации.
Эта процедура повторяется для всех узлов, в прямом и обратном порядке, аналогично тому, как в варианте без ограничений осуществлялись перемещения. При этом, ограничение «эллипс», вероятно, является характеристикой ребра, а не узла, т.о. на второй фазе перемещаться на эллипс должен узел p[3] — прим. перев.
