[Перевод] Занимательная задачка о просачивании шестиугольников
Ровно 50%.
Доказательство основывается на простой идее: если существует путь из синих шестиугольников, соединяющий синие участки границы ромба, тогда не существует пути из белых шестиугольников, соединяющего белые участки границы. А если не существует пути из синих шестиугольников, соединяющего синие участки границы ромба, тогда существует путь из белых шестиугольников, соединяющий белые участки границы.
Суть игры Blockbusters была построена именно на этом: участникам при помощи правильных ответов на вопросы нужно было либо построить путь, ведущий сверху вниз, либо путь, ведущий слева направо. Не могло быть такой ситуации, когда существуют оба пути, или когда ни одного пути не существует — это гарантировало выигрыш одной из сторон.
Однако одной этой идеи недостаточно. Надо также доказать, что синий путь существует ровно в половине конфигураций раскраски ромба. Для этого начнём с одной произвольной конфигурации — например, такой, как на картинке ниже. На ней есть синий путь, соединяющий синие участки границы, и нет белого пути, соединяющего белые:

Инвертируем ситуацию, поменяв все синие шестиугольники на белые, а белые — на синие:

Зеркально отразим ромб так, чтобы его левая верхняя часть оказалась левой нижней, а правая верхняя — правой нижней:
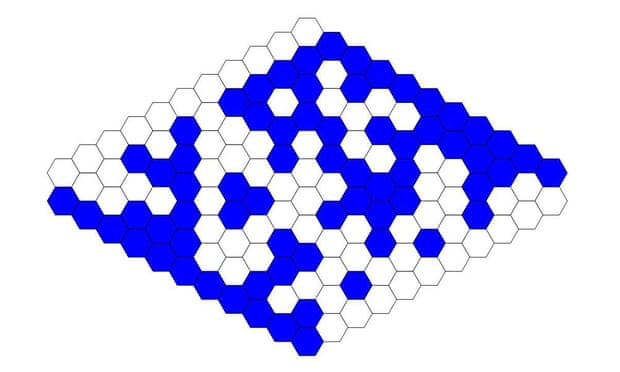
То есть, мы начали с конфигурации, в которой есть синий путь, соединяющий синие границы, и превратили её в конфигурацию, в которой нет синего пути, соединяющего синие границы. А если мы повторим нашу процедуру — поменяем цвета на противоположные, и отразим ромб по горизонтали — то вернёмся к изначальной конфигурации.
Наоборот, если бы мы начали с конфигурации, в которой нет синего пути, соединяющего синие границы, это означало бы, что в ней есть путь, соединяющий белые границы. Повторив процедуру «меняем цвета, отражаем ромб», мы бы пришли к конфигурации, в которой был бы синий путь, соединяющий синие границы. Повторив этот процесс снова, мы вернулись бы к первоначальной конфигурации.
Следовательно, мы можем заключить, что какую бы конфигурацию раскраски ромба мы ни выбрали, она будет частью пары конфигураций. В одной из этих двух конфигураций есть синий путь, соединяющий синие границы, а в другой — белый путь, соединяющий белые.
Как упоминалось ранее, не существует такой конфигурации, в которой одновременно есть и синий путь между синими границами, и белый путь между белыми.
А если у каждой конфигурации есть пара, то количество конфигураций, в которых есть синий путь между синими границами, должно равняться количеству конфигураций, в которых есть белый путь между белыми границами. Поэтому доля конфигураций, содержащих синий путь, равна ровно 50%.
При чём же тут кофе?
Как я уже упоминал, перколяция как область исследований занимается вопросом проникновения жидкостей через пористые материалы. Шестиугольная решётка — это модель материала, а каждая синяя ячейка может, например, обозначать наличие поры, в которую может просочиться жидкость. Теоретикам перколяции интересны такие вопросы, как, например, в каком проценте от общего числа всех возможных конфигураций сетки есть синий путь?
Как следует из задачки, когда вероятность того, что шестиугольник будет синим, а не белым, равна 50%, тогда нужный путь есть у 50% конфигураций. А что будет, если мы поменяем вероятность того, что шестиугольник может быть синим — уменьшим или увеличим её? А что, если у нас будет больше двух вариантов состояний каждого шестиугольника? Ответы на подобные вопросы помогли учёным понять поведение материалов при фазовых переходах — когда одна базовая структура материала внезапно меняется на другую. Эти ответы находят применение в физике, биологии, экологии и теории сетей.
