[Перевод] Трёхмерная графика с нуля. Часть 2: растеризация24.11.2017 12:18

image

Первая часть статьи может быть доказательством того, что трассировщики лучей — это изящный пример программного обеспечения, позволяющий создавать потрясающе красивые изображения исключительно с помощью простых и интуитивно понятных алгоритмов.

К сожалению, эта простота имеет свою цену: низкую производительность. Несмотря на то, что существует множество способов оптимизации и параллелизации трассировщиков лучей, они всё равно остаются слишком затратными с точки зрения вычислений для выполнения в реальном времени; и хотя оборудование продолжает развиваться и становится быстрее с каждым годом, в некоторых областях применения необходимы красивые, но в сотни раз быстрее создаваемые изображения уже сегодня. Из всех этих областей применения самыми требовательными являются игры: мы ожидаем рендеринга отличной картинки с частотой не менее 60 кадров в секунду. Трассировщики лучей просто с этим не справятся.

Тогда как это удаётся играм?

Ответ заключается в использовании совершенно иного семейства алгоритмов, которое мы исследуем во второй части статьи. В отличие от трассировки лучей, которая получалась из простых геометрических моделей формирования изображений в человеческом глазе или в камере, сейчас мы будем начинать с другого конца — зададимся вопросом, что мы можем отрисовать на экране, и как отрисовать это как можно быстрее. В результате мы получим совершенно другие алгоритмы, которые создают примерно похожие результаты.

Прямые
Снова начнём с нуля: у нас есть холст с размерами $C_w$ и $C_h$, и мы можем расположить на нём пиксель ($PutPixel()$).

Допустим, у нас есть две точки, $P_0$ и $P_1$ с координатами $(x_0, y_0)$ и $(x_1, y_1)$. Отрисовка этих двух точек по отдельности тривиальна;, но как можно отрисовать отрезок прямой линии из $P_0$ в $P_1$?

Давайте начнём с представления прямой с параметрическими координатами, как мы делали это ранее с лучами (эти «лучи» — не что иное, как прямые в 3D). Любую точку на прямой можно получить, начав с $P_0$ и переместившись на какое-то расстояние в направлении от $P_0$ к $P_1$:

$P = P_0 + t(P_1 - P_0)$


Мы можем разложить это уравнение на два, по одному для каждой из координат:

$x = x_0 + t(x_1 - x_0)$


$y = y_0 + t(y_1 - y_0)$


Давайте возьмём первое уравнение и вычислим $t$:

$x = x_0 + t(x_1 - x_0)$


$x - x_0 = t(x_1 - x_0)$


${{x - x_0} \over {x_1 - x_0}} = t$


Теперь мы можем подставить это выражение во второе уравнение вместо $t$:

$y = y_0 + t(y_1 - y_0)$


$y = y_0 + {{x - x_0} \over {x_1 - x_0}}(y_1 - y_0)$


Немного преобразуем его:

$y = y_0 + (x - x_0){{y_1 - y_0} \over {x_1 - x_0}}$


Заметьте, что ${{y_1 - y_0} \over {x_1 - x_0}}$ — это постоянная, зависящая только от конечных точек отрезка; давайте обозначим её $a$:

$y = y_0 + a(x - x_0)$


Что же такое $a$? Судя по тому, как она определена, она является показателем изменения координаты $y$ на изменение единицы длины координаты $x$; другими словами, это показатель наклона прямой.

Давайте вернёмся к уравнению. Раскроем скобки:

$y = y_0 + ax - ax_0$


Группируем константы:

$y = ax + (y_0 - ax_0)$


Выражение $(y_0 - ax_0)$ снова зависит только от конечных точек отрезка; давайте обозначим его $b$, и наконец получим

$y = ax + b$


Это классическая линейная функция, которой можно представить почти все прямые. Ею нельзя описать вертикальные прямые, потому что они имеют бесконечное количество значений $y$ при одном значении $x$, и ни одного при всех остальных. Иногда в процессе получения такого представления из исходного параметрического уравнения такие семейства прямых можно упустить; это происходит при вычислении $t$, потому что мы проигнорировали то, что $x_1 - x_0$ может давать деление на ноль. Пока давайте просто проигнорируем вертикальные прямые; позже мы избавимся от этого ограничения.

Итак, теперь у нас есть способ вычисления значения $y$ для любого интересующего нас значения $x$. При этом мы получим пару $(x, y)$, удовлетворяющую уравнению прямой. Если мы будем двигаться от $x_0$ к $x_1$ и вычислять значение $y$ для каждого значения $x$, то получим первое приближение нашей функции отрисовки прямой: 

DrawLine(P0, P1, color) {
    a = (y1 - y0)/(x1 - x0)
    b = y0 - a*x0
    for x = x0 to x1 {
        y = a*x + b
        canvas.PutPixel(x, y, color)
    }
}


В этом фрагменте x0 и y0 — это координаты $x$ и $y$ точки P0; в дальнейшем я буду использовать эту удобную запись. Также заметьте, что оператор деления / должен выполнять не целочисленное деление, а деление вещественных чисел.

Эта функция является непосредственной наивной интерпретацией приведённого выше уравнения, поэтому очевидно, что она работает;, но можем ли мы ускорить её работу?

Заметьте, что мы не вычисляем значения $y$ для всех $x$: на самом деле, мы вычисляем их только как целочисленные инкременты $x$, и мы делаем это в следующем порядке: сразу после вычисления $y(x)$ мы вычисляем $y(x+1)$:

$y(x) = ax + b$


$y(x+1) = a(x+1) + b$


Мы можем воспользоваться этим для создания более быстрого алгоритма. Давайте возьмём разность между $y$ последовательных пикселей:

$y(x+1) - y(x) = (a(x+1) + b) - (ax + b)$


$= a(x+1) + b - ax - b$


$= ax + a - ax$


$= a$


Это не очень удивительно; в конце концов, наклон $a$ — это показатель того, насколько $y$ меняется на каждую единицу инкремента $x$, то есть именно то, что мы здесь делаем.

Интересно то, что мы можем тривиальным образом получить следующее:

$y(x+1) = y(x) + a$


Это значит, что мы можем вычислить следующее значение $y$ только с помощью предыдущего значения $y$ и прибавлением наклона; попиксельное умножение не требуется. Нам нужно с чего-то начать (в самом начале нет никакого «предыдущего значения $y$», поэтому мы начнём с $(x_0, y_0)$, а затем будем прибавлять $1$ к $x$ и $a$ к $y$, пока мы не доберёмся до $x_0$.

Считая, что $x_0 < x_1$, мы можем переписать функцию следующим образом: 

DrawLine(P0, P1, color) {
    a = (y1 - y0)/(x1 - x0)
    y = y0
    for x = x0 to x1 {
        canvas.PutPixel(x, y, color)
        y = y + a
    }
}


Эта новая версия функции имеет новое ограничение: она может отрисовывать прямые только слева направо, то есть при $x_0 < x_1$. Эту проблему довольно просто обойти: поскольку неважно, в каком порядке мы отрисовываем отдельные пиксели, то если у нас будет прямая справа налево, мы просто поменяем P0 и P1, чтобы превратить её в лево-правую версию той же прямой, после чего отрисуем её как раньше: 

DrawLine(P0, P1, color) {
    # Make sure x0 < x1
    if x0 > x1 {
        swap(P0, P1)
    }
    a = (y1 - y0)/(x1 - x0)
    y = y0
    for x = x0 to x1 {
        canvas.PutPixel(x, y, color)
        y = y + a
    }
}


Теперь мы можем отрисовать пару прямых. Вот $(-200, 100) - (240, 120)$:

e993d6f116f20948b153411d4b566965.png

Вот как она выглядит вблизи:

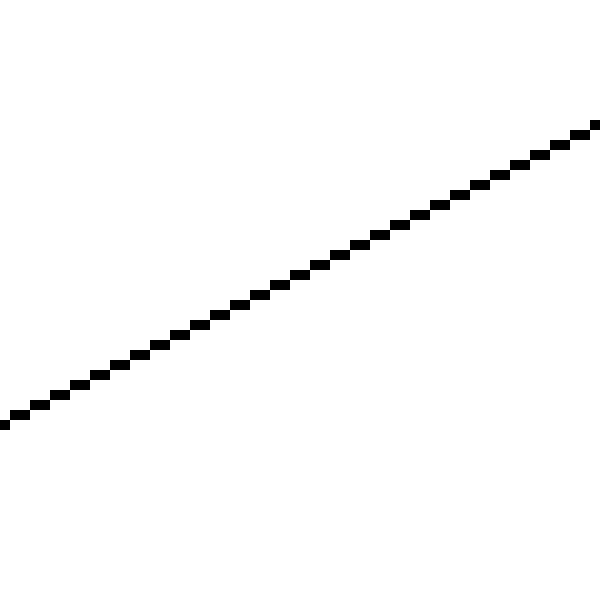
3c3c5c4d6799e45fcadc7024d1ef4aed.png

Прямая выглядит ломаной потому, что мы можем рисовать пиксели только по целочисленным координатам, а математические прямые на самом деле имеют нулевую ширину; рисуемое нами является дискретизированным приближением к идеальной прямой $(-200, 100) - (240, 120)$ (Примечание: существуют способы отрисовки более красивых приближенных прямых. Мы не будем использовать по двум причинам: 1) это медленнее, 2) наша цель — не рисовать красивые прямые, а разработать базовые алгоритмы для рендеринга 3D-сцен.).

Давайте попробуем нарисовать ещё одну прямую, $(-50, -200) - (60, 240)$:

0cb0ac1aeb9cc257c9bb7099a7060463.png

А вот как она выглядит вблизи:

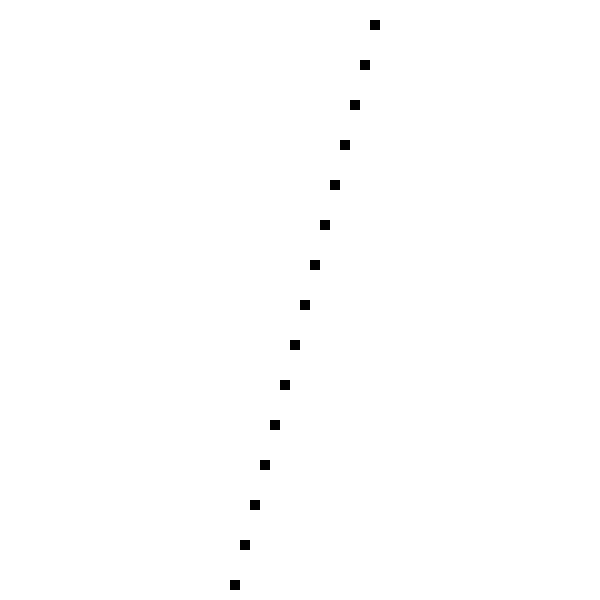
6bd9c236acc6ad73c6de62c761c93b97.png

Ой. Что случилось?

Алгоритм работал так, как и задумано; он прошёл слева направо, вычислил значение $y$ для каждого значения $x$ и отрисовал соответствующий пиксель. Проблема в том, что он вычислял одно значение $y$ для каждого значения $x$, в то время как для некоторых значений $x$ нам нужно несколько значений $y$.

Это прямое последствие выбора формулировки, в которой $y = f(x)$; на самом деле по той же самой причине мы не можем рисовать вертикальные прямые, предельный случай, при котором есть одно значение $x$ с несколькими значениями $y$.

Мы без всяких проблем можем рисовать горизонтальные прямые. Почему же нам не удаётся так же просто отрисовывать вертикальные линии?

Как оказывается, мы можем это сделать. Выбор $y = f(x)$ был произвольным решением, поэтому нет никаких причин, мешающих выразить прямую как $x = f(y)$, переработав все уравнения и поменяв $x$ и $y$, чтобы в результате получить следующий алгоритм: 

DrawLine(P0, P1, color) {
    # Make sure y0 < y1
    if y0 > y1 {
        swap(P0, P1)
    }
    a = (x1 - x0)/(y1 - y0)
    x = x0
    for y = y0 to y1 {
        canvas.PutPixel(x, y, color)
        x = x + a
    }
}


Это аналогично предыдущей DrawLine, за исключением перемены мест вычислений $x$ и $y$. Полученная функция может справляться с вертикальными линиями и сможет правильно отрисовать $(0, 0) - (50, 100)$; разумеется, она не справится с горизонтальными прямыми и не сможет правильно отрисовать $(0, 0) - (100, 50)$! Что же нам делать?

Нам просто нужно выбирать нужную версию функции в зависимости от прямой, которую нужно нарисовать. И критерии будут достаточно простыми; имеет ли прямая более различающиеся значения $x$ или $y$? Если есть больше значений $x$, чем $y$, мы используем первую версию; в противном случае применяется вторая.

Вот версия DrawLine, обрабатывающая все случаи: 

DrawLine(P0, P1, color) {
    dx = x1 - x0
    dy = y1 - y0
    if abs(dx) > abs(dy) {
        # Прямая ближе к горизонтальной
        # Проверяем, что x0 < x1
        if x0 > x1 {
            swap(P0, P1)
        }
        a = dy/dx
        y = y0
        for x = x0 to x1 {
            canvas.PutPixel(x, y, color)
            y = y + a
        }
    } else {
        # Прямая ближе к вертикальной
        # Проверяем, что y0 < y1
        if y0 > y1 {
            swap(P0, P1)
        }
        a = dx/dy
        x = x0
        for y = y0 to y1 {
            canvas.PutPixel(x, y, color)
            x = x + a
        }
    }
}


Это безусловно сработает, но код не особо красив; в нём есть две реализации кода, инкрементно вычисляющих линейную функцию, и эта логика вычислений и выбора перемешана. Поскольку мы будем часто использовать линейные функции, то стоит потратить немного времени на разделение кода.

У нас есть две функции, $y = f(x)$ и $x = f(y)$. Чтобы абстрагироваться от того, что мы работаем с пикселями, давайте запишем это в общем виде как $d = f(i)$, где $i$ — независимая переменная, для которой мы выбираем значения, а $d$ — зависимая переменная, значения которой зависят от другой, и которую мы хотим вычислить. В случае более горизонтальной прямой $x$ является независимой переменной, а $y$ — зависимой; в случае более вертикальной прямой всё наоборот.

Разумеется, любую функцию можно записать как $d = f(i)$. Мы знаем ещё два аспекта, полностью задающие её: её линейность и два её значения;, а именно, $d_0 = f(i_0)$ и $d_1 = f(i_1)$. Мы можем написать простой метод, получающий эти значения и возвращающий промежуточные значения $d$, полагая, как и ранее, что $i1 < i0$: 

Interpolate (i0, d0, i1, d1) {
    values = []
    a = (d1 - d0) / (i1 - i0)
    d = d0
    for i = i0 to i1 {
        values.append(d)
        d = d + a
    }
    return values
}


Заметьте, что значение $d$, соответствующее $i_0$, находится в values[0], значение для $i_0 + 1$ находится в values[1], и так далее; в общем случае, значение $i_n$ находится в values[i_n - i_0], если считать, что $i_n$ находится в интервале $[i_0, i_1]$.

Существует тупиковый случай, который нужно учитывать; нам может понадобиться вычислить $d = f(i)$ для единственного значения $i$, то есть при $i0 = i1$. В этом случае мы не можем даже вычислить $a$, поэтому мы будем обрабатывать это как особый случай: 

Interpolate (i0, d0, i1, d1) {
    if i0 == i1 {
       return [ d0 ]
    }
    values = []
    a = (d1 - d0) / (i1 - i0)
    d = d0
    for i = i0 to i1 {
        values.append(d)
        d = d + a
    }
    return values
}


Теперь мы можем написать DrawLine с использованием Interpolate: 

DrawLine(P0, P1, color) {
    if abs(x1 - x0) > abs(y1 - y0) {
        # Прямая ближе к горизонтальной
        # Проверяем, что x0 < x1
        if x0 > x1 {
            swap(P0, P1)
        }
        ys = Interpolate(x0, y0, x1, y1)
        for x = x0 to x1 {
            canvas.PutPixel(x, ys[x - x0], color)
        }
    } else {
        # Прямая ближе к вертикальной
        # Проверяем, что y0 < y1
        if y0 > y1 {
            swap(P0, P1)
        }
        xs = Interpolate(y0, x0, y1, x1)
        for y = y0 to y1 {
            canvas.PutPixel(xs[y - y0], y, color)
        }
    }
}


Этот DrawLine может правильно обрабатывать все случаи:

9fd7bb565de76a75a906aaaa1f7ce715.png

Исходный код и рабочее демо >>

Хотя эта версия не сильно короче предыдущей, она чётко разделяет вычисление промежуточных значений $y$ и $x$, решение о выборе независимой переменной плюс сам код отрисовки. Преимущество этого возможно не совсем очевидно, но мы будем снова активно использовать Interpolate в последующих главах.

Следует учесть, что это не самый лучший или быстрый алгоритм отрисовки; важным результатом этой главы стал Interpolate, а не DrawLine. Лучшим алгоритмом отрисовки линий скорее всего является алгоритм Брезенхэма.

Заполненные треугольники
Мы можем использовать метод DrawLine для отрисовки контура треугольника. Такой тип контура называется каркасным, потому что он выглядит как каркас треугольника: 

DrawWireframeTriangle (P0, P1, P2, color) {
    DrawLine(P0, P1, color);
    DrawLine(P1, P2, color);
    DrawLine(P2, P0, color);
}


Мы получим вот такой результат:

2eb76d71fe5344ec6f0920e29428defe.png

Можем ли мы залить треугольник каким-нибудь цветом?

Как обычно бывает в компьютерной графике, для этого есть множество способов. Мы будем отрисовывать заполненные треугольники, воспринимая их как набор отрезков горизонтальных прямых, которые, если их отрисовать вместе, выглядят как треугольник. Ниже представлено очень грубое первое приближение того, что мы хотим сделать: 

для каждой координаты y горизонтальной прямой, занятой треугольником
    вычислить x_left и x_right для этого y
    DrawLine(x_left, y, x_right, y)


Давайте начнём с части «для каждой координаты y горизонтальной прямой, занятой треугольником». Треугольник задаётся тремя вершинами $P_0$, $P_1$ и $P_2$. Если мы отсортируем эти точки, увеличивая значение $y$, таким образом, что $y_0 \le y_1 \le y_2$, то интервал значений $y$, занятых треугольником, будет равен $[y_0, y_2]$: 

if y1 < y0 { swap(P1, P0) }
if y2 < y0 { swap(P2, P0) }
if y2 < y1 { swap(P2, P1) }


Затем нам нужно вычислить x_left и x_right. Это немного сложнее, потому что у треугольника три, а не две стороны. Однако с точки зрения значений $y$ у нас всегда есть «длинная» сторона от $P_0$ до $P_2$ и две «короткие» стороны от $P_0$ до $P_1$ и от $P_1$ lj $P_2$ (Примечание: существует особый случай, когда $y_0 = y_1$ или $y_1 = y_2$, то есть когда у треугольника есть горизонтальная сторона; в таких случаях есть две стороны, которые можно считать «длинными» сторонами. К счастью, не важно, какую сторону мы выберем, поэтому можно придерживаться этого определения.). То есть значения x_right получаются или от длинной стороны, или от обеих коротких сторон;, а значения x_left получаются от другого множества.

Мы начнём с вычисления значений $x$ для трёх сторон. Так как мы отрисовываем горизонтальные отрезки, то нам нужно ровно одно значение $x$ для каждого значения $y$; это значит, что мы можем получить значения непосредственно с помощью Interpolate, используя в качестве независимого значения $y$, а в качестве зависимого значения $x$: 

x01 = Interpolate(y0, x0, y1, x1)
x12 = Interpolate(y1, x1, y2, x2)
x02 = Interpolate(y0, x0, y2, x2)


x02 будет или x_left, или x_right; другой будет конкатенацией x01 и x12.

Заметьте, что в этих двух списках есть повторяющееся значение: значение $x$ для $y_1$ является и последним значением x01, и первым значением x12. Нам просто нужно избавиться от одного из них.

remove_last(x01)
x012 = x01 + x12


Наконец у нас есть x02 и x012, и нам нужно определить, что из них является x_left и x_right. Для этого надо посмотреть на значения $x$ для одной из прямых, например, для средней: 

m = x02.length / 2
if x02[m] < x012[m] {
    x_left = x02
    x_right = x012
} else {
    x_left = x012
    x_right = x02
}


Теперь осталось только отрисовать горизонтальные отрезки. По причинам, которые станут понятны позже, мы не будем использовать для этого DrawLine; вместо этого мы будем отрисовывать пиксели по отдельности.

Вот полная версия DrawFilledTriangle: 

DrawFilledTriangle (P0, P1, P2, color) {
    # Сортировка точек так, что y0 <= y1 <= y2
    if y1 < y0 { swap(P1, P0) }
    if y2 < y0 { swap(P2, P0) }
    if y2 < y1 { swap(P2, P1) }

    # Вычисление координат x рёбер треугольника
    x01 = Interpolate(y0, x0, y1, x1)
    x12 = Interpolate(y1, x1, y2, x2)
    x02 = Interpolate(y0, x0, y2, x2)

    # Конкатенация коротких сторон
    remove_last(x01)
    x012 = x01 + x12

    # Определяем, какая из сторон левая и правая
    m = x012.length / 2
    if x02[m] < x012[m] {
        x_left = x02
        x_right = x012
    } else {
        x_left = x012
        x_right = x02
    }

    # Отрисовка горизонтальных отрезков
    for y = y0 to y2 {
        for x = x_left[y - y0] to x_right[y - y0] {
            canvas.PutPixel(x, y, color)
        }
    }
}


Вот результат; для проверки мы вызвали DrawFilledTriangle, а потом DrawWireframeTriangle с одинаковыми координатами, но разными цветами:

04df4c93b53ff4020b19f3ef13b27ab5.png

Исходный код и рабочее демо >>

Вы можете заметить, что чёрный контур треугольника не полностью совпадает с зелёной внутренней областью; это особенно заметно в правом нижнем ребре треугольника. Так получилось потому, что DrawLine () вычисляет $y = f(x)$ для этого ребра, но DrawTriangle () вычисляет $x = f(y)$. На такую аппроксимацию мы готовы пойти, чтобы достичь нашей цели — высокоскоростного рендеринга.

Затенённые треугольники
В предыдущей части мы разработали алгоритм для отрисовки треугольника и заливки его цветом. Нашей следующей целью будет отрисовка затенённого треугольника, который похож на залитый градиентом.

Хотя затенённые треугольники выглядят красивее, чем одноцветные, это не является основной целью главы; это просто особое применение техники, которую мы создадим. Наверно, она будет самой важной в этом разделе статьи; почти всё остальное будет построено на её основе.

Но давайте начнём с простого. Вместо заполнения треугольника сплошным цветом, мы хотим заполнить его оттенками цвета. Это будет выглядеть так:

d9507e16f5e369dbf4dcbb3a9447c73a.png

Исходный код и рабочее демо >>

Первый шаг заключается в формальном определении того, что мы хотим отрисовать. Для этого мы назначим каждой вершине вещественное значение $h$, обозначающее яркость цвета вершины. $h$ находится в интервале $[0.0, 1.0]$.

Чтобы получить точный цвет пикселя, имея цвет $C$ и яркость $h$, мы просто выполним поканальное умножение: $C_h = (R_C*h, G_C*h, B_C*h)$. То есть при $h = 0.0$ мы получим чёрный, а при $h = 1.0$ — исходный цвет $C$.

Вычисление затенения ребра


Итак, для отрисовки затенённого треугольника нам нужно вычислить значение $h$ для каждого пикселя треугольника, получить соответствующий оттенок цвета и закрасить пиксель. Всё очень просто!

Однако на этом этапе мы знаем только значения $h$ для заданных вершин. Как вычислить значения $h$ для остальной части треугольника?

Давайте сначала рассмотрим рёбра. Выберем ребро $AB$. Мы знаем $h_A$ и $h_B$. Что происходит в $M$, то есть в середине отрезка $AB$? Поскольку мы хотим, чтобы яркость плавно изменялась от $A$ к $B$, то $h_M$ должно быть каким-то значением между $h_A$ и $h_B$. Так как $M$ — это средняя точка отрезка $AB$, то почему бы не сделать $h_M$ средним значением $h_A$ и $h_B$?

Если более формально, то у нас есть функция $h = f(P)$, для которой нам известны предельные значения $h(A)$ и $h(B)$, и нам нужно сделать её плавной. Мы больше ничего не знаем об $h = f(P)$, поэтому можем выбрать любую функцию, соответствующую этим критериям, например, линейную функцию:

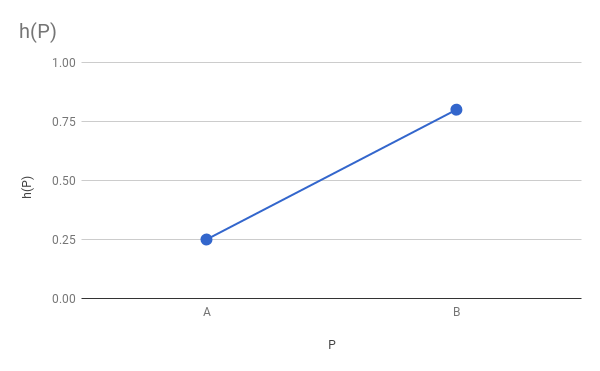
4dd4cefe1ccb3f8660d9bfc6d47e9b4a.png

Разумеется, основой кода затенённого треугольника будет код сплошного треугольника, созданный в предыдущей главе. Один их первых шагов включает в себя вычисление конечных точек каждого горизонтального отрезка, то есть x_left и x_right для сторон $P_0P_1$, $P_0P_2$ и $P_1P_2$; мы использовали Interpolate() для вычисления значений $x = f(y)$, имея $x(y_0)$ и $x(y_1)$… и именно это мы и хотим сделать здесь, достаточно просто заменить $x$ на $h$!

То есть мы можем вычислить промежуточные значения $h$ точно таким же образом, как мы вычисляли значения $x$: 

x01 = Interpolate(y0, x0, y1, x1)
h01 = Interpolate(y0, h0, y1, h1)

x12 = Interpolate(y1, x1, y2, x2)
h12 = Interpolate(y1, h1, y2, h2)

x02 = Interpolate(y0, x0, y2, x2)
h02 = Interpolate(y0, h0, y2, h2)


Следующим этапом будет превращение этих трёх векторов в два вектора и определение того, какой из них представляет левосторонние значения, а какой — правосторонние. Заметьте, что значения $h$ не играют никакой роли в том, что чем является; это полностью определяется значениями $x$. Значения $h$ «приклеиваются» к значениям $x$, потому что являются другими атрибутами тех же физических пикселей. То есть, если x012 имеет значения для правой стороны треугольника, тогда h012 имеет значения для правой стороны треугольника: 

  # Конкатенация коротких сторон
  remove_last(x01)
  x012 = x01 + x12

  remove_last(h01)
  h012 = h01 + h12

  # Определяем, какая из сторон левая и правая
  m = x012.length / 2
  if x02[m] < x012[m] {
      x_left = x02
      x_right = x012

      h_left = h02
      h_right = h012
  } else {
      x_left = x012
      x_right = x02

      h_left = h012
      h_right = h02
  }


Вычисление внутреннего затенения


Остался единственный шаг — отрисовка самих горизонтальных отрезков. Для каждого отрезка мы знаем $x_{left}$ и $x_{right}$, а теперь мы также знаем $h_{left}$ и $h_{right}$. Однако вместо итерирования слева направо и отрисовки каждого пикселя базовым цветом нам нужно вычислить значения $h$ для каждого пикселя отрезка.

Мы снова можем считать, что $h$ линейно изменяется с $x$ и использовать Interpolate() для вычисления этих значений: 

h_segment = Interpolate(x_left[y-y0], h_left[y-y0], x_right[y-y0], h_right[y-y0])


И теперь это просто вопрос вычисления цвета для каждого пикселя и его отрисовки.

Вот код вычисления для DrawShadedTriangle: 

DrawShadedTriangle (P0, P1, P2, color) {
    # Сортировка точек так, что y0 <= y1 <= y2
    if y1 < y0 { swap(P1, P0) }
    if y2 < y0 { swap(P2, P0) }
    if y2 < y1 { swap(P2, P1) }

    # Вычисление координат x и значений h для рёбер треугольника
    x01 = Interpolate(y0, x0, y1, x1)
    h01 = Interpolate(y0, h0, y1, h1)

    x12 = Interpolate(y1, x1, y2, x2)
    h12 = Interpolate(y1, h1, y2, h2)

    x02 = Interpolate(y0, x0, y2, x2)
    h02 = Interpolate(y0, h0, y2, h2)

    # Конкатенация коротких сторон
    remove_last(x01)
    x012 = x01 + x12

    remove_last(h01)
    h012 = h01 + h12

    # Определяем, какая из сторон левая и правая
    m = x012.length / 2
    if x02[m] < x012[m] {
        x_left = x02
        x_right = x012

        h_left = h02
        h_right = h012
    } else {
        x_left = x012
        x_right = x02

        h_left = h012
        h_right = h02
    }

    # Отрисовка горизонтальных отрезков
    for y = 
    
            
© Habrahabr.ru