[Перевод] Тождество Эйлера — самое красивое математическое уравнение
Мы уже писали об удивительном свойстве числа e, которое может помочь, когда вслепую из конечного числа вариантов нужно выбрать единственный вариант. Сегодня давайте вспомним о тождестве Эйлера — по праву самом красивом уравнении, важное место в котором занимает число e, но не только оно. Представьте на секунду, что вы почти ничего не знаете о математике, только начинаете открывать её бесконечную красоту — и наслаждайтесь.
Все мы знаем о числе π — магическом отношении длины окружности к её диаметру. Число π можно приближённо представить в виде дроби 22/7. Особенность числа π состоит в том, что в его десятичной записи знаки после запятой никогда не заканчиваются. Его приближённое значение — 3,141592653589793238… Вот почему π называют иррациональным числом — его нельзя записать в виде конечного числа цифр после запятой. А вот другое интересное иррациональное число — e. Число e — это «число Эйлера» (от Euler). Вот первые несколько цифр числа e: 2,7182818284590…
Мало того, что это число иррациональное, оно применяется буквально во всех областях математики. Оно используется в логарифмических функциях как основание логарифма. Мы называем такой логарифм натуральным и записываем его так: ln x.
Что означает эта запись? В натуральном логарифме f(x)=ln(x) — это степень, в которую нужно возвести число e, чтобы получить x. Как же рассчитать значение e, спросите вы? Есть несколько способов.
Вот один из них: e — это предел последовательности, общий член которой равняется (1+ 1/n)ⁿ. Вот ещё один: площадь области под графиком y=1/x от x=1 до x=e равняется одному единичному квадрату.
Ещё один способ определения e: посмотрите на ряд 1 + 1/1! + ½! + ⅓! + ¼! +…. Сумма этого ряда равняется e.
Чтобы вы почувствовали, насколько важным может быть число e, рассмотрим пример. Предположим, есть стеллаж с книгами, на каждой полке которого стоит только одна конкретная книга. Предположим также, что кто-то скинет на пол все книги и вы начнёте подбирать их с пола одну за одной и снова ставить на полки. Вероятность того, что каждая книга попадёт не на свою полку, составляет примерно 1/e. Чем больше книг, тем ближе такая вероятность будет к значению 1/e.
Поговорим теперь о другом интересном математическом объекте. Он называется просто: i. Разберёмся, что это такое.
Если умножить 2 на 2, получится 4. То есть 2 в квадрате равняется 4. Квадрат положительного числа — это положительное число. Но, если возвести в квадрат –2, также получится 4, то есть положительное число. Другими словами, ни один квадрат действительного числа не может быть отрицательным числом. Вот тут-то и возникает понятие мнимого числа.
Число √-1 записывается буквой i. i означает мнимую (imaginary) единицу. То есть запись √-5 можно заменить записью √5 i. Отсюда следует, что i² = -1. Число i формирует множество комплексных чисел, то есть комбинаций действительных и мнимых чисел. Например, запись 8 + i√5 является комплексным числом. Для визуализации комплексных чисел используется плоскость мнимых чисел.
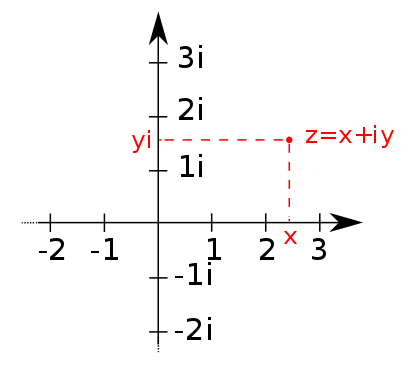 Комплексные числа. Источник: Wikimedia Commons
Комплексные числа. Источник: Wikimedia CommonsИзучать свойства комплексных чисел математики начали примерно с середины XVIII века. Однажды Эйлер развлекался с женой Тейлора… ох, простите… с рядом Тейлора. Ряд Тейлора:
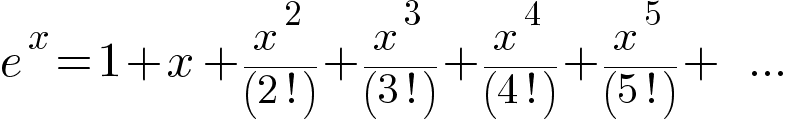
Этому сумасброду просто стало интересно, как будет вести себя ряд Тейлора, если подставить в него число i (а что, вполне нормальная мысль для любого сумасброда).

И вот что у него начало получаться:
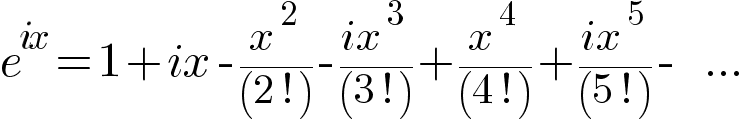
Но i² = -1 (Ух! Меня уже начинает охватывать научный азарт!) Сгруппируем все члены ряда, содержащие i.
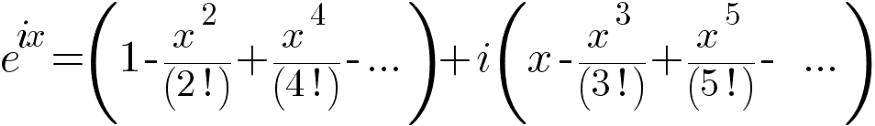
Догадываетесь, что будет дальше? Одни члены ряда, содержащие i, сводятся в одну группу, а другие, не содержащие мнимую часть, то есть без числа i, — в другую. Получаются два ряда Тейлора: один — для косинуса, другой — для синуса.

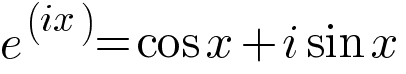
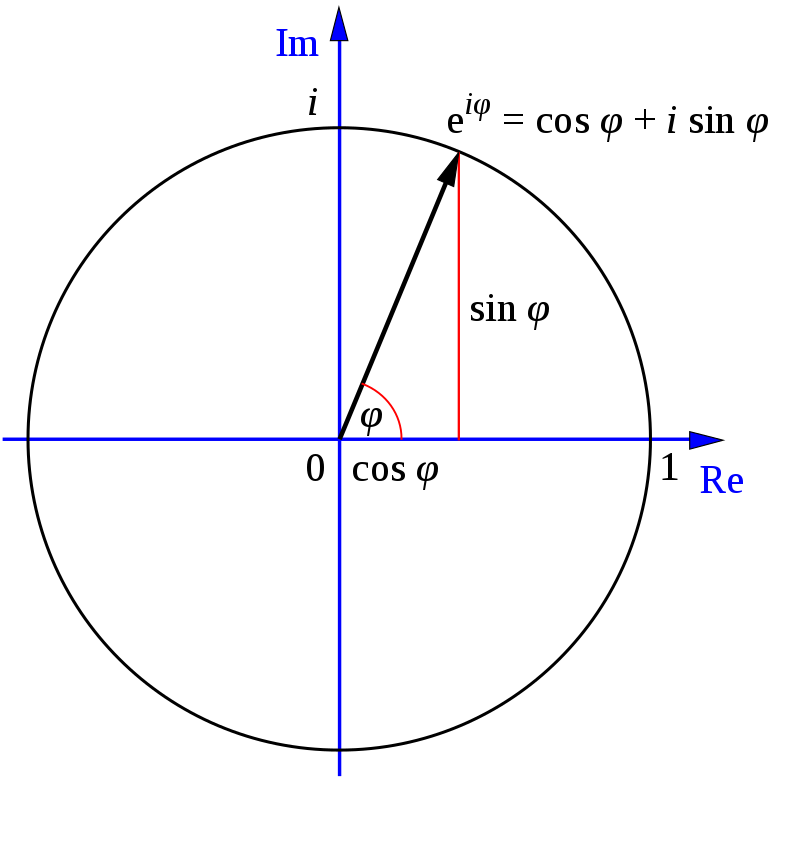
Мы получили знаменитую формулу Эйлера. Различные значения x и e^(ix) можно отразить на комплексной плоскости. Например,

Это комплексное число, которое может быть представлено на комплексной плоскости. Если продолжить наносить на график точки e^(ix) для разных значений x, получится окружность.
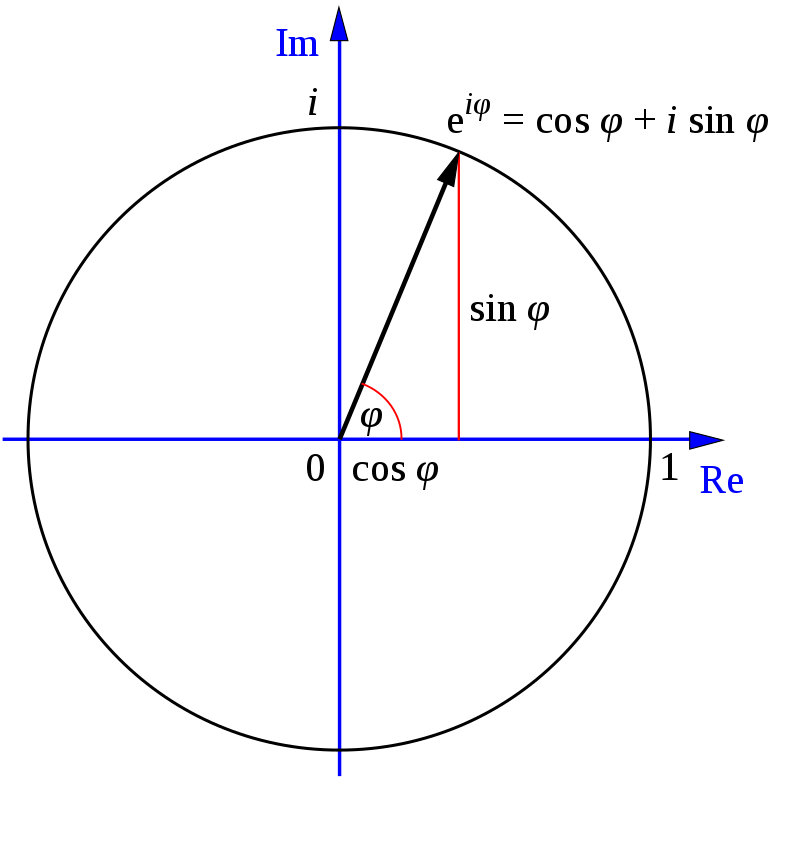 Формула Эйлера. Источник: Wikimedia Commons
Формула Эйлера. Источник: Wikimedia CommonsЕсли нужно узнать радиус r в любой точке (например, в точке 5 + 7i), рассчитывается значение x и берётся действительная часть re^(ix). Наконец, если в формулу Эйлера подставить значение x = π, получаем:
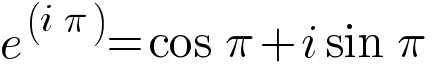

(поскольку cos π = −1 и sin π = 0).
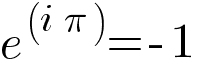
Объединив три самых необыкновенных математических символа, получаем магическое уравнение:
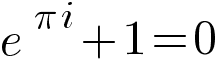
Вот оно перед вами — по мнению математиков, самое красивое уравнение во всей математике. Оно называется Тождеством Эйлера.
Приходите на курс «математика для Data Science» — и наши менторы покажут, как при помощи математики менять мир к лучшему. Но даже если менять мир в ваши планы пока не входит — там можно будет подтянуть математическую базу. Будет сложно, но интересно.

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:
Другие профессии и курсыПРОФЕССИИ
КУРСЫ
