[Перевод] Теория вероятностей для физически точного рендеринга

Введение
В рендеринге часто используется вычисление многомерных определённых интегралов: например, для определения видимости пространственных источников освещения (area light), светимости, доходящей до области пикселя, светимости, поступающей за период времени и облучения, поступающего через полусферу точки поверхности. Вычисление этих интегралов обычно выполняется при помощи интегрирования Монте-Карло, в котором интеграл заменяется ожиданием стохастического эксперимента.
В этой статье я подробно расскажу о базовом процессе интегрирования Монте-Карло, а также о нескольких техниках, позволяющих снизить дисперсию методики. Это будет сделано с практической точки зрения — предполагается, что читатель не сильно знаком с теорией вероятностей, но всё равно хочет разрабатывать эффективные и корректные алгоритмы рендеринга.
Определённые интегралы
Определённый интеграл — это интеграл вида , где
— это отрезок (или область),
— скаляр, а
— функция, которая может быть вычислена для любой точки отрезка. Как написано в Википедии, определённый интеграл — это площадь со знаком на плоскости
, ограниченная графиком
, осью
и вертикальными линиями
и
(Рисунок 1a).
Эта концепция логично распространяется и на более высокое количество измерений: для определённого двойного интеграла площадь со знаком становится объёмом со знаком (Рисунок 1b), а в общем для определённых многократных интегралов он становится многомерным объёмом со знаком.
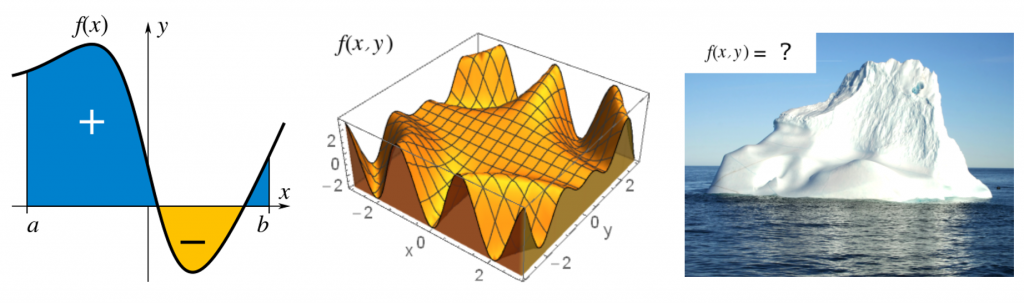
Рисунок 1: примеры определённых интегралов.
В некоторых случаях площадь можно определить аналитически, например, для : на отрезке
площадь будет равна
. В иных случаях аналитическое решение невозможно, например, когда нам нужно узнать объём части айсберга, находящейся над водой (Рисунок 1c). В таких случаях
часто можно определить сэмплированием.
Численное интегрирование
Мы можем приблизительно вычислить площадь сложных интегралов с помощью численного интегрирования. Один из примеров — это сумма Римана. Эта сумма вычисляется разделением области на правильные фигуры (например, прямоугольники), которые вместе образуют область, похожую на истинную область. Сумма Римана задаётся следующим образом:
— это количество подинтервалов, а
— ширина одного подинтервала. Для каждого интервала
мы сэмплируем
в одной точке
внутри подинтервала (на Рисунке 2 эта точка находится в начале подинтервала).
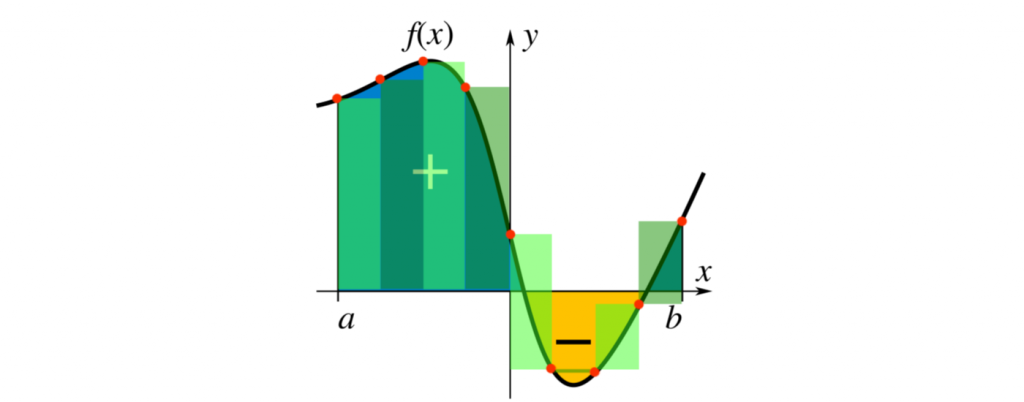
Рисунок 2: сумма Римана.
Стоит заметить, что при увеличении сумма Римана сходится к действительному значению интеграла:
Сумма Римана может использоваться и при больших размерностях (Рисунок 3). Однако здесь мы сталкиваемся с проблемой: для функции с двумя параметрами количество подинтервалов должно быть намного больше, если мы хотим достичь разрешения, сравнимого с тем, которое применялось в двухмерном случае. Это явление называют проклятием размерностей, и в более высоких размерностях оно усугубляется.

Рисунок 3: сумма Римана для двойного интеграла.
Сейчас мы оценим точность суммы Римана для следующей функции (мы намеренно выбрали сложную функцию):
График функции на отрезке показан ниже. Для справки мы вычислили в Wolfram Alpha определённый интеграл
, получив площадь
. График справа показывает точность численного интегрирования с помощью суммы Римана для увеличивающегося
.
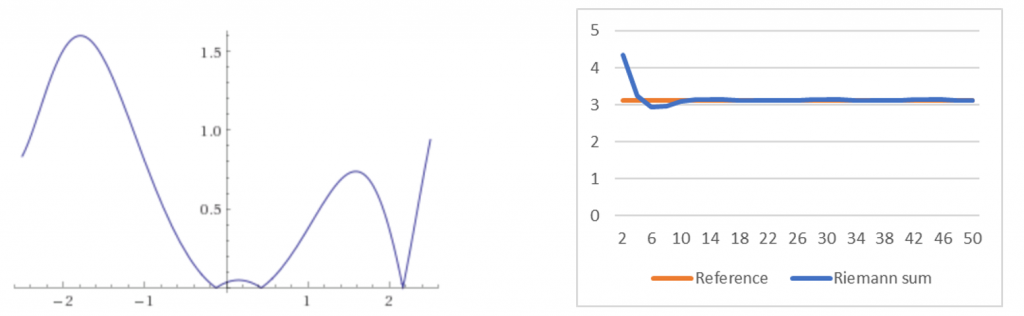
Рисунок 4: график функции и точность суммы Римана. Даже при небольших мы получаем достаточно точный результат.
Чтобы получить представление о точности, приведём числа: при погрешность составляет
. При
погрешность составляет
. Следующий порядок величин получается при
.
Дополнительную информацию о суммах Римана можно прочитать на следующих ресурсах:
Монте-Карло (1)
При рендеринге почти никакие (а может быть, вообще никакие?) интегралы не являются однократными. Это значит, что мы быстро столкнёмся с проклятием размерностей. Кроме того, сэмплирование функции на равных интервалах подвержено недостаточности выборки и искажениям: мы можем пропустить важные значения функции или получить непредусмотренные взаимные помехи между сэмплируемой функцией и паттерном сэмплирования (Рисунок 5).
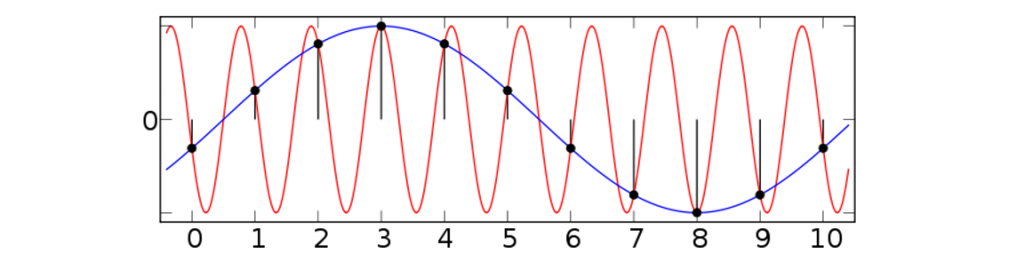
Рисунок 5: искажения приводят к потере частей сэмплируемой функции (красная) и, в этом случае, к полностью неверной интерпретации функции.
Эти проблемы решаются при помощи техники, называемой интегрированием Монте-Карло. Аналогично сумме Римана, в ней тоже используется сэмплирование функции во множестве точек, но в отличие от детерминированного паттерна суммы Римана мы применяем фундаментально недетерминированный ингредиент: случайные числа.
Интегрирование Монте-Карло основано на следующем наблюдении: интеграл можно заменить ожиданием стохастического эксперимента:
Другими словами, мы сэмплируем функцию раз в случайных точках в пределах отрезка (обозначаемого заглавной
), усредняем сэмплы и умножаем на ширину отрезка (для одномерной функции). Как и в случае суммы Римана, при стремлении
к бесконечности среднее значение сэмплов сходится к ожиданию, то есть к истинному значению интеграла.
Немного теории вероятностей
Здесь важно понимать каждое из используемых понятий. Давайте начнём с ожидания: это значение, ожидаемое для одного сэмпла. Учтите, что это не обязательно возможное значение, что может показаться нелогичным. Например, когда мы бросаем кубик, ожидание равно — среднему всех возможных исходов:
.
Второе понятие — это случайные числа. Это может показаться очевидным, но для интегрирования Монте-Карло нам требуются равномерно распределённые случайные числа, т.е. каждое значение должно иметь равную вероятность генерации. Подробнее об этом мы поговорим позже.
Третье понятие — это отклонение и связанная с ним дисперсия. Даже когда мы возьмём небольшое количество чисел, ожидаемое среднее значение, а также ожидание каждого отдельного сэмпла должно быть одинаковым. Однако при вычислении уравнения 4 мы редко будем получать такое значение. Отклонение — это разность между ожиданием и исходом эксперимента: .
На практике это отклонение имеет интересное распределение:
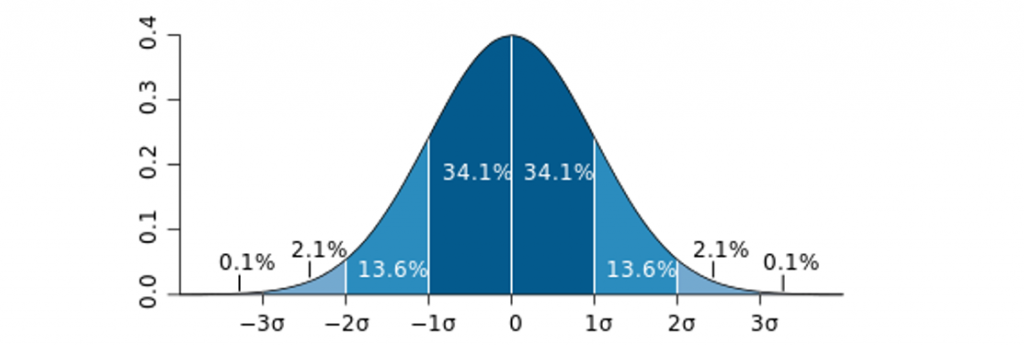
Это график нормального распределения, или распределения Гаусса: он показывает, что не все отклонения одинаково вероятны. На самом деле, примерно 68,2% сэмплов находится в интервале , где
(сигма) — это стандартное отклонение. Стандартное отклонение можно описать двумя способами:
- Стандартное отклонение — это мера изменчивости данных.
- 95% точек данных находятся в пределах
от среднего.
Для определения стандартного отклонения существует два метода:
- Стандартное отклонение
: его можно вычислить, если есть дискретное распределение вероятностей и известно ожидание
. Это истинно для кубиков, у которых
и
. Подставив числа, получим
.
- Также стандартное отклонение сэмплов можно вычислить как
. Подробнее об этом можно прочитать в Википедии.
Проверка: правильно ли это? Если, то мы заявляем, что 68,2% сэмплов находятся в пределах 1,71 от 3,5. Мы знаем, что
удовлетворяют этому критерию, а
и
— нет. Четыре из шести — это 66,7%. Если бы наш кубик мог выдавать любое значение в интервале
, то мы бы получили ровно 68,2%.
Вместо стандартного отклонения часто используют связанное понятие дисперсии, которое определяется как . Поскольку используется квадрат, дисперсия всегда положительна, что помогает в вычислениях.
Монте-Карло (2)
Выше мы приближённо вычислили уравнение 3 при помощи суммы Римана. Теперь мы повторим этот эксперимент с интегрированием Монте-Карло. Вспомним, что интегрирование Монте-Карло задаётся следующим образом:
Переведём это в код на C:
double sum = 0;
for( int i = 0; i < n; i++ ) sum += f( Rand( 5 ) - 2.5 );
sum = (sum * 5.0) / (double)n;
Результат для значений от до
показан на графике ниже. Из него можно предположить, что интегрирование Монте-Карло проявляет себя гораздо хуже, чем сумма Римана. Более внимательное изучение погрешности говорит, что при
средняя погрешность суммы Римана равна
, а у Монте-Карло —
.
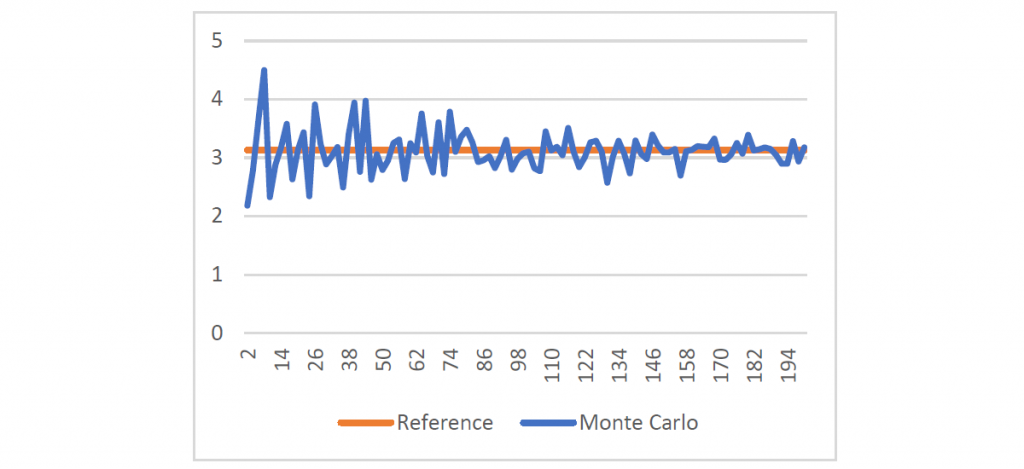
Рисунок 6: погрешность Монте-Карло при 2…200 сэмплах.
В более высоких размерностях эта разница снижается, но не устраняется полностью. Показанное ниже уравнение является развёрнутой версией использованного выше, получающее два параметра:

Рисунок 7: график представленного выше уравнения.
В области определения объём, ограниченный этой функцией и плоскостью
, равен
. При
(20×20 сэмплов) погрешность суммы Римана равна
. При том же количестве сэмплов средняя погрешность интегрирования Монте-Карло составляет
. Это лучше, чем предыдущий результат, но разница всё равно значительна. Чтобы разобраться в этой проблеме, мы изучим хорошо известную технику снижения дисперсии для интегрирования Монте-Карло под названием «стратификация».
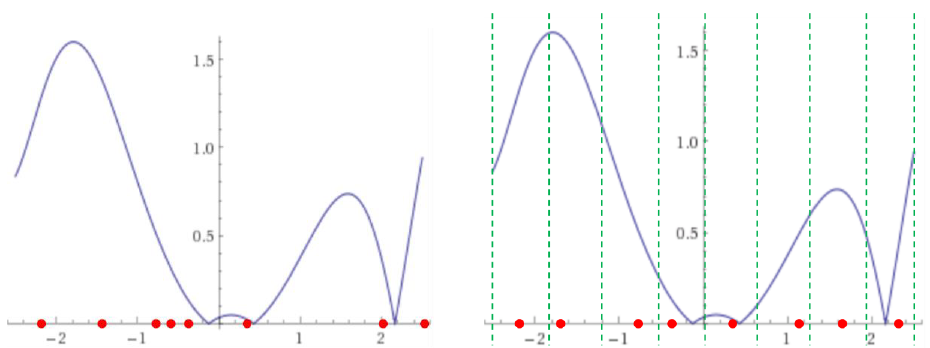
Рисунок 8: влияние стратификации; a) сэмплы с плохим распределением; b) сэмплы с равномерным распределением.
Стратификация повышает равномерность случайных чисел. На Рисунке 8a для сэмплирования функции используются восемь случайных чисел. Так как каждое число выбирается случайным образом, часто они оказываются неравномерно распределёнными по области определения. На Рисунке 8b показано влияние стратификации: область определения разделена на восемь страт, и в каждой страте выбирается случайная позиция, что улучшает равномерность.
Влияние на дисперсию достаточно очевидно. На Рисунке 9a показан график результатов со стратификацией и без неё. На Рисунке 9b показана погрешность приблизительного значения. При средняя погрешность для 8 страт равна
; для 20 страт —
, а для 200 страт она снижается до
. Исходя из этих результатов кажется, что стоит использовать большое количество страт. Однако стратификация обладает недостатками, усиливающимися при увеличении количества страт. Во-первых, количество сэмплов всегда должно быть кратно количеству страт; во-вторых, как и в сумме Римана, стратификация страдает от проклятья размерностей.
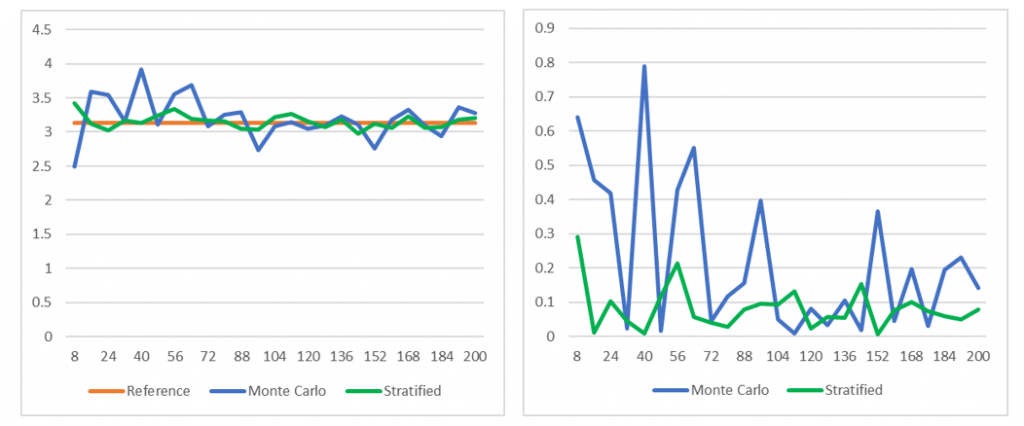
Рисунок 9: стратификация и дисперсия: a) приблизительное значение при количестве сэмплов от n=2 до n=200; b) отклонение.
Выборка по значимости
В предыдущих разделах мы сэмплировали уравнения равномерно. Расширение интегрирующей функции Монте-Карло позволяет нам изменить ситуацию:
Здесь — это функция распределения вероятностей (probability density function, pdf): она определяет относительную вероятность того, что случайная величина примет определённое значение.
Для равномерной случайной величины в интервале , pdf равняется 1 (Рисунок 10a), и это значит, что каждое значение имеет одинаковую вероятность выбора. Если мы проинтегрируем эту функцию по
, то получим вероятность в
того, что
. Для
Рисунок 10: распределения вероятностей. a) постоянная pdf, при которой каждый сэмп имеет равную вероятность выбора; b) pdf, при которой сэмплы ниже 0.5 имеют бОльшую вероятность выбора.
На Рисунке 10b показана другая pdf. В данном случае вероятность генерации числа меньше равна 70%. Это можно реализовать при помощи следующего фрагмента кода:
float SamplePdf()
{
if (Rand() < 0.7f) return Rand( 0.5f );
else return Rand( 0.5f ) + 0.5f;
}
Эта pdf задаётся следующим образом:
Числа и
отражают необходимость того, что вероятность
была равна 70%. При интегрировании pdf по
даёт
, а
равно
. Это иллюстрирует важное требование для всех pdf в целом: результат интегрирования pdf должен быть равен 1. Ещё одно требование заключается в том, что
не может быть равна нулю, если
не равна нулю: это бы значило, что части
имеют нулевую вероятность сэмплирования, что, очевидно, влияет на значение.
Несколько подсказок, позволяющих уяснить концепцию pdf:
- Одно значение pdf не описывает вероятность: следовательно, локально pdf может быть больше 1 (например, как в только что рассмотренной pdf).
- Однако интеграл по области определения pdf является вероятностью, а значит, что интегрирование pdf даёт 1.
Одно значение можно интерпретировать как относительную возможность появления конкретного значения.
Стоит учесть, что нормальное распределение — это функция распределения вероятностей: оно даёт нам вероятность того, что какая-то случайная величина будет находиться в определённом интервале. В случае нормального распределения эта случайная величина является отклонением от среднего. Как и любая приличная pdf, результат интегрирования нормального распределения равно 1.
Следовательно, уравнение 7 позволяет нам выполнять неравномерное сэмплирование. Оно компенсирует его делением каждого сэмпла на относительную вероятность его выбора. Важность этого показана на Рисунке 11a. График функции демонстрирует значительный интервал, в котором её значение равно . Сэмплирование в этой области бессмысленно: к сумме ничего не прибавляется, мы просто делим на большее число. Вспомните айсберг с Рисунка 1c: нет смысла сэмплировать высоту в большой площади вокруг айсберга.
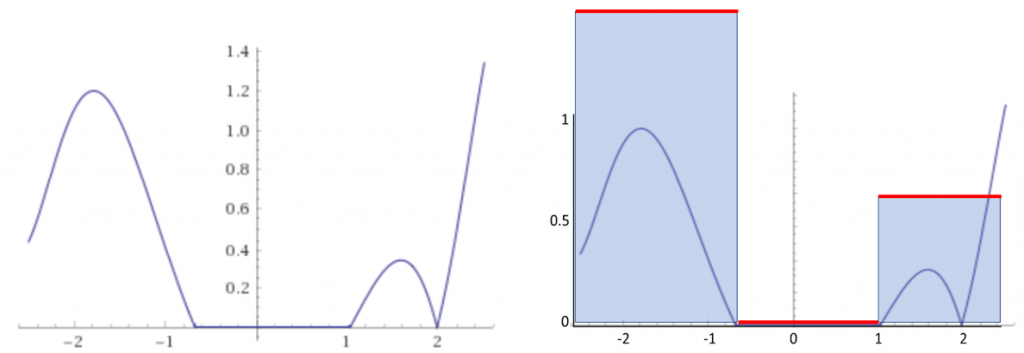
Рисунок 11: pdf для функции с нулевыми значениями.
Pdf, использующая это знание о функции, показана на Рисунке 11b. Заметьте, что эта pdf на самом деле равна нулю для интервала значений. Это не превращает её в неправильную pdf: в некоторых местах функция равна нулю. Мы можем расширить эту идею за пределы нулевых значений. Сэмплы лучше всего тратить на те места, в которых функция имеет значимые значения. На самом деле, идеальная pdf пропорциональна сэмплируемой функции. Очень хорошая pdf для нашей функции показана на Рисунке 12a. Ещё более качественная pdf показана на Рисунке 12b. В обоих случаях мы не должны забывать нормализовать её, чтобы интеграл равнялся 1.
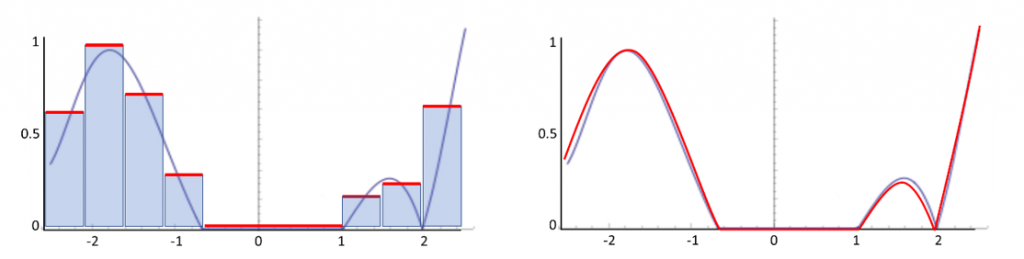
Рисунок 12: улучшенные pdf для функции на Рисунке Figure 11.
Pdf на Рисунке 12 ставят перед нами две задачи:
- как создать такие pdf;
- как сэмплировать такие pdf?
Ответ на оба вопроса одинаков: нам этого делать не нужно. Во многих случаях функция, которую мы хотим интегрировать, неизвестна, и единственный способ определения мест, в которых она значима — это её сэмплирование, и именно для этого нам и нужна pdf; классическая ситуация «курицы и яйца».
Однако в других случаях у нас есть примерное представление о том, где функция может давать более высокие значения или нулевые значения. В таких случаях очень приблизительная pdf часто лучше, чем никакой pdf.
Также у нас может иметься возможность создания pdf «на лету». Пара сэмплов дают представление о форме функции, и на основании неё мы нацеливаем последующие сэмплы в те места, где ожидаем высоких значений, которые используем для улучшения pdf, и так далее.
В следующей статье мы применим эти концепции к реализации рендеринга. Серьёзной сложностью является построение pdf. Мы исследуем несколько случаев, когда pdf помогают в сэмплировании.
