[Перевод] Теория Связей 0.0.102.04.2024 00:00

В прошлое первое апреля, как вы могли догадаться, мы пошутили. Пора это исправить, и теперь $100\%$ всё серьёзно.

Сравнение теорий

Начнём мы со сравнения математических основ двух самых популярных теорий и ассоциативной теории. Это позволит быстро ввести читателя в контекст.

Реляционная алгебра

Реляционная алгебра и реляционная модель основаны на понятиях отношения и n-кортежей.

Отношение определяется как множество n-кортежей:

$\mathbf{R \subseteq S_1 \times S_2 \times \dots \times S_n}.$ [1]

Где:

$\mathbf{R}$ обозначает отношение (таблицу);
$\mathbf{S_n}$ обозначает область определения каждого столбца;
Строки или элементы множества $\mathbf{R}$ представлены в виде n-кортежей.

Данные в реляционной модели группируются в отношения. Используя n-кортежи в реляционной модели, можно точно представить любую возможную структуру данных. Но нужны ли вообще n-кортежи? Например, каждый n-кортеж можно представить в виде вложенных упорядоченных пар (2-кортежей). Также не часто встретишь, что значения столбцов в таблицах представляются n-кортежами (хотя, например, число можно разложить на n-кортеж битов). В некоторых базах данных даже запрещено использовать более $\mathbf{32}$ столбцов в таблице и ее строке (n-кортеже). Так что $\mathbf{N}$ обычно меньше $\mathbf{32}$ . Поэтому, в этом случае, нет реальных n-кортежей, даже в современных реляционных базах данных.

Ориентированный граф

Направленный граф и графы в целом основаны на понятиях вершины и ребра (2-кортежа).

Направленный граф $\mathbf{G}$ определяется как упорядоченная пара $\mathbf{G(V, E)}$ :

$\mathbf{G(V, E) = \langle V, E \rangle, \quad V \neq \emptyset, \quad \langle \{ v_1, v_2 \}, \prec \rangle \in E, \quad v \in V}.$

Где:

$\mathbf{V}$ — это множество, элементы которого называются вершинами, узлами или точками;
$\mathbf{E}$ — это множество упорядоченных пар (2-кортежей) вершин, называемых дугами, направленными ребрами (иногда просто ребрами), стрелками или направленными линиями.

Данные в модели графа представлены в виде двух отдельных множеств узлов и ребер, и можно использовать эту модель практически для всего, кроме, вероятно, последовательностей (n-кортежей). Ну, возможно, их можно представить последовательности в виде множеств, но на наш взгляд это не практичный способ представления последовательностей. Вероятно, не одни мы так считаем, что может объяснить, почему мы не смогли найти примеры, в которых другие люди так делали.

Ассоциативная теория

Ассоциативная теория основана на понятии связи.

Связь определяется как n-кортеж ссылок на связи.

Дуплеты

Дуплет также известен как 2-кортеж или упорядоченная пара.

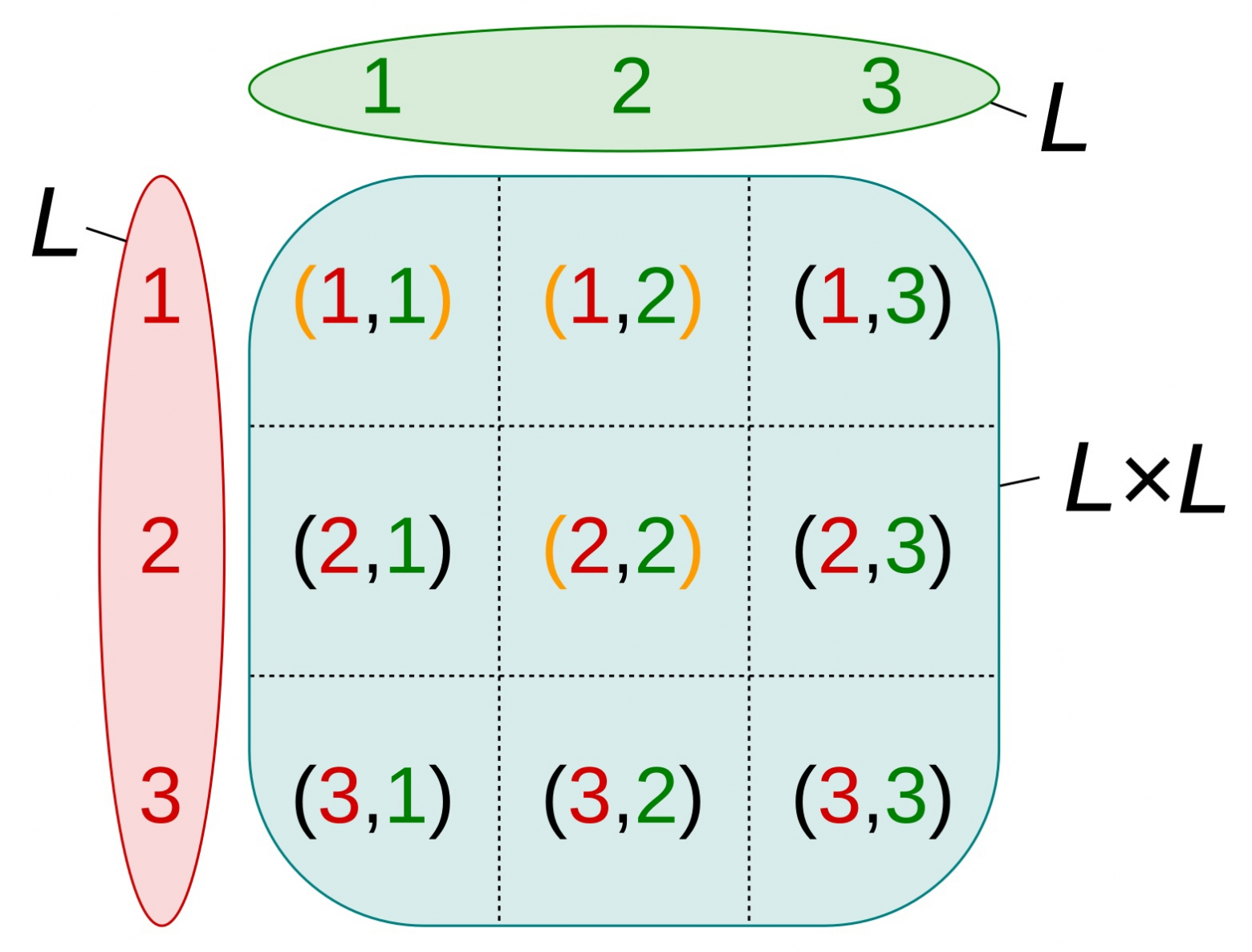
L = { 1 , 2 }

L × L = {
  (1, 1),
  (1, 2),
  (2, 1),
  (2, 2),
}

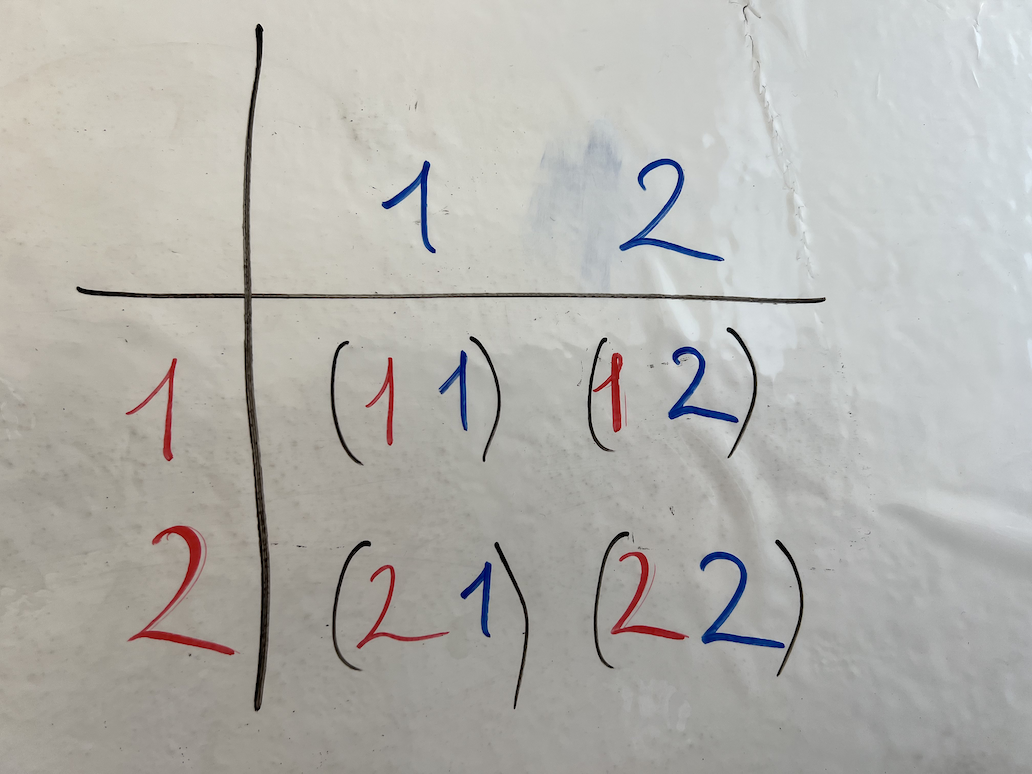
alt text

Матрица представляющая декартово произведение множества { 1, 2 } на само себя.

alt text

Таблица строк содержащих все возможные варианты декартова произведения { 1, 2 } на само себя.

Сеть дуплетов определяется как:

$\mathbf{\lambda: L \to L \times L.}$

Где:

$\mathbf{\lambda}$ обозначает функцию, которая определяет сеть дуплетов;
$\mathbf{L}$ обозначает множество индексов связей.

Пример:

$1 \to (1, 1)$
$2 \to (2, 2)$
$\mathbf{3 \to (1, 2)}$

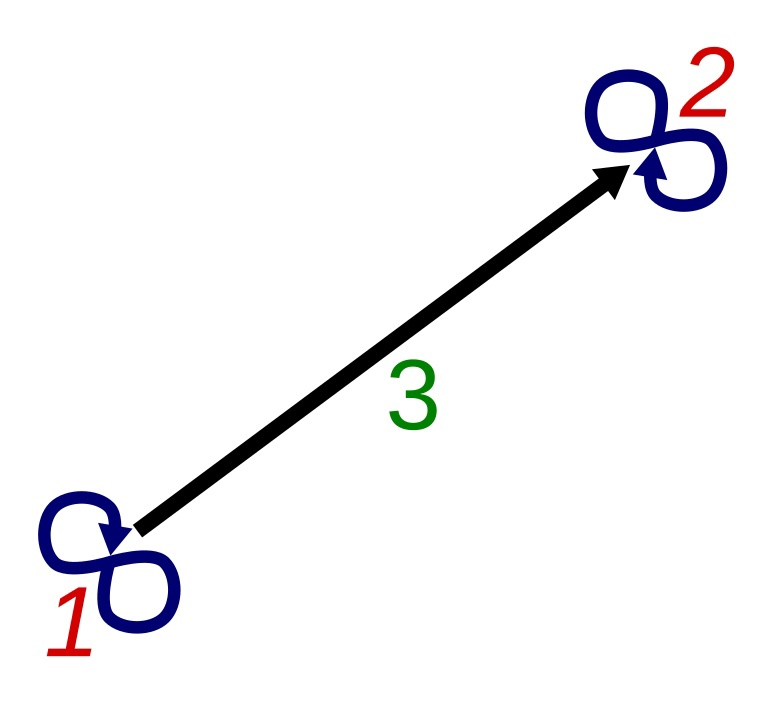
alt text

Сеть из трёх связей. Представление сети дуплетов похожее на граф, но такую визуализацию мы называем сетью связей.

alt text

Это графическое представление декартова произведения в виде матрицы, которое представляет все возможные значения связей. Значения связей с оранжевыми скобками выбраны функцией $\mathbf{\lambda}$ в примере. Этот выбор и задаёт сеть связей.

Данные в сети дуплетов представлены с использованием дуплетов (2-кортежей).

Дуплеты могут:

связывать объект со своими свойствами;
связывать два дуплета вместе, чего не позволяет теория графов;
представлять любую последовательность (n-кортеж) в виде дерева, построенного из вложенных упорядоченных пар.

Благодаря этому дуплеты могут представлять, как мы верим, любую возможную структуру данных.

Триплеты

Триплет также известен как 3-кортеж.

L = { 1 , 2 }

L × L = {
  (1, 1),
  (1, 2),
  (2, 1),
  (2, 2),
}

L × L × L = {
  (1, 1, 1),
  (1, 1, 2),
  (1, 2, 1),
  (1, 2, 2),
  (2, 1, 1),
  (2, 1, 2),
  (2, 2, 1),
  (2, 2, 2),
}

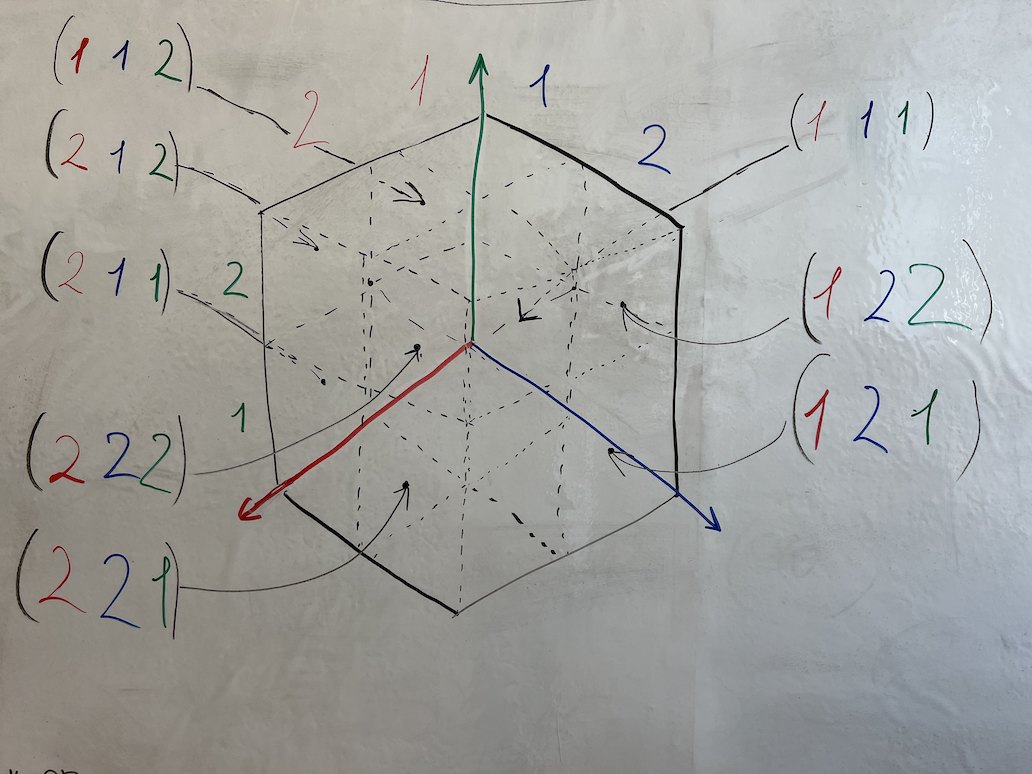
alt text

Трёхмерный куб-матрица, который представляет все возможные значения связи-триплета. Получить такой куб можно используя декартово произведение множества { 1, 2 } на само себя, рекурсивно, то есть { 1, 2 } × { 1, 2 } × { 1, 2 }.

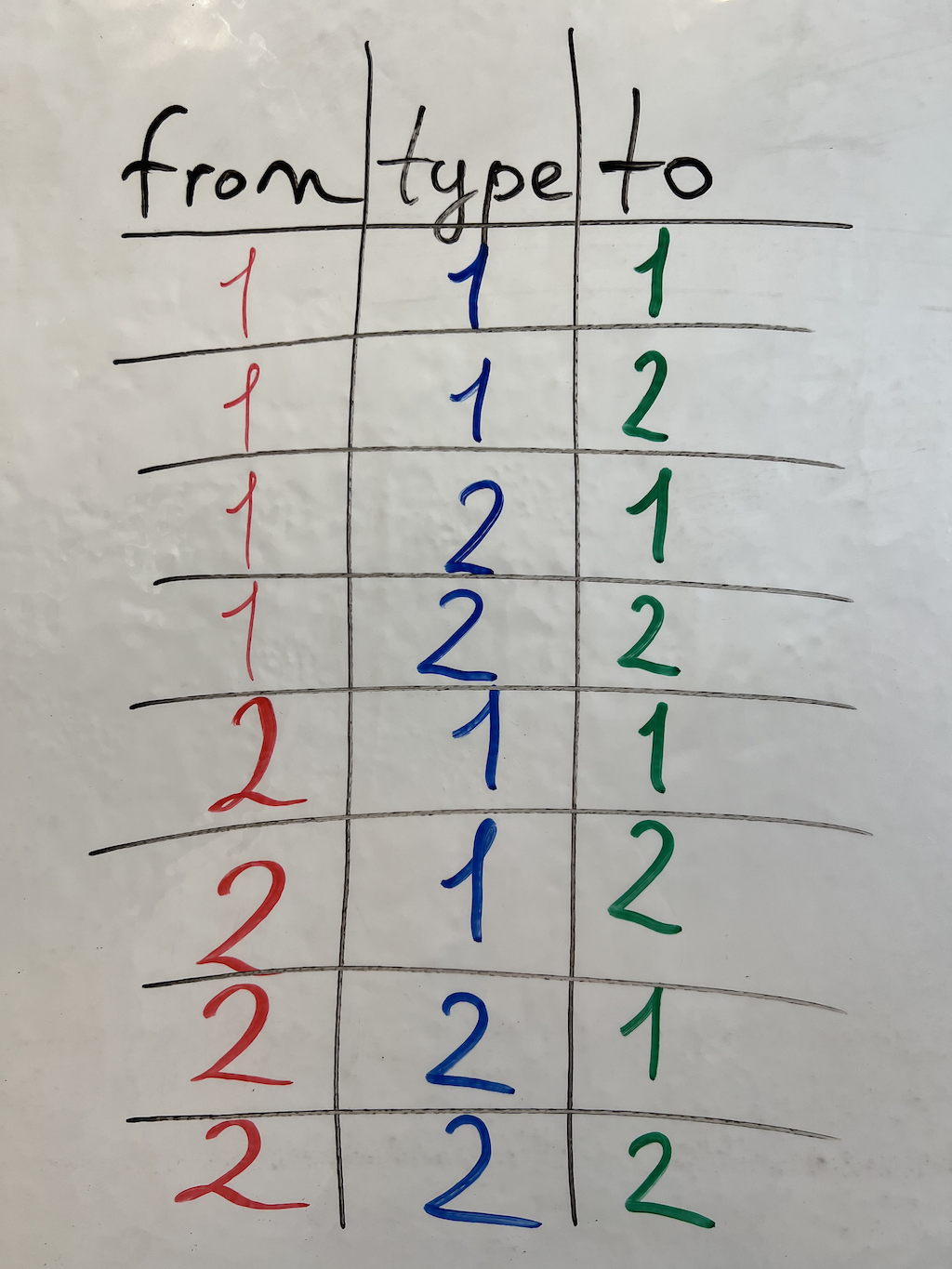
alt text

Таблица всех возможных вариантов значения связи-триплета, которую можно получить используя декартово произведение множества { 1, 2 } на само себя, рекурсивно, то есть { 1, 2 } × { 1, 2 } × { 1, 2 }.

Сеть триплетов определяется как:

$\mathbf{\lambda : L \to L \times L \times L.}$

Где:

$\mathbf{\lambda}$ обозначает функцию, определяющую сеть триплетов;
$\mathbf{L}$ обозначает набор индексов ссылок.

Пример:

$1 \to (1, 1, 1)$
$2 \to (2, 2, 2)$
$3 \to (3, 3, 3)$
$\mathbf{4 \to (1, 2, 3)}$

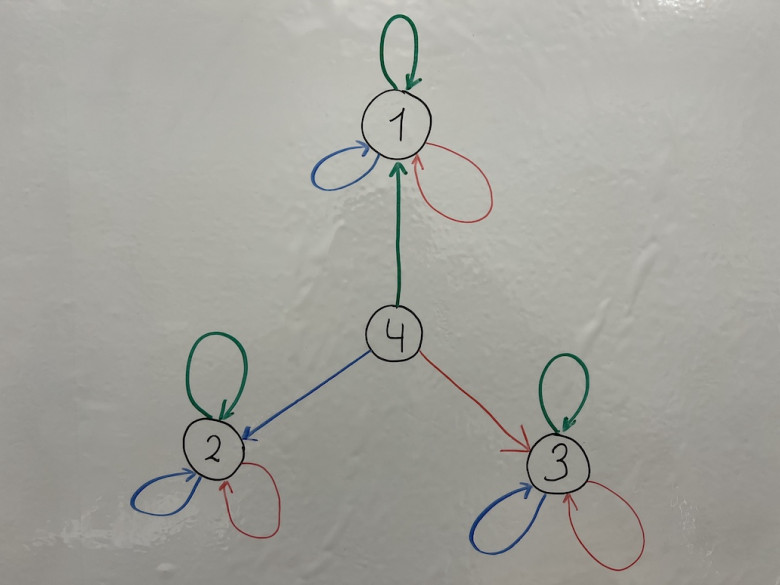
alt text

Графо-подобное сетевое представление 4-х связей-триплетов.

Данные в сети триплетов представлены с использованием триплетов (3-кортежей).

Триплеты могут делать то же, что и дуплеты, а также позволяют указывать типы или значения непосредственно для каждой ссылки.

Вектора

Вектор (последовательность) также известный как n-кортеж, является общим случаем.

Сеть связей в общем виде определяется так:

$\mathbf{\lambda : L \rightarrow \underbrace{ L \times L \times \ldots \times L}_{n}.}$

Где:

$\mathbf{\lambda}$ обозначает функцию, определяющую сеть связей;
$\mathbf{L}$ обозначает набор индексов ссылок.

Пример:

$1 \to (1)$
$2 \to (2, 2)$
$3 \to (3, 3, 3)$
$\mathbf{4 \to (1, 2, 3, 2, 1)}$

В этом примере используются n-кортежи переменной длины для значений связей.

Последовательности по сути эквивалентны по выразительной силе реляционной модели. И это ещё предстоит доказать в рамках разрабатываемой теории. Но когда было замечено, что дуплеты и триплеты достаточны для представления последовательностей любого размера, то появилось предположение об отсутвии необходимости использовать сами последовательности напрямую.

Итоги сравнения

Реляционная модель данных может представить все, включая ассоциативную модель. Графовая же модель особенно хороша в представлении отношений и не так хороша в представлении последовательностей.

Ассоциативная модель может легко представить n-кортеж неограниченной длины с использованием кортежей с $\mathbf{n \geq 2}$ , она столь же хороша, как теория графов, в своей способности представлять ассоциации, и она также мощна, как реляционная модель, и может полностью представить любую таблицу SQL.

В реляционной модели нет необходимости в более чем одном отношении, чтобы заставить ее вести себя как ассоциативная модель. И в этом отношении нет необходимости в более чем 2–3 столбцах, кроме явного ID или встроенного ID строки.

Графовая модель не имеет возможности напрямую создавать ребро между ребрами по определению. Поэтому графовой модели требуется либо изменить свое определение, либо расширить его с помощью некоторого дополнительного способа хранения последовательностей. Возможно, на самом деле можно хранить последовательности в виде вложенных наборов внутри графовой модели, но этот способ не популярен. Графовая модель — ближайшая модель к дуплетам, но она все равно отличается по определению.

Использование ассоциативной модели означает, что больше не нужно выбирать между базами данных SQL и NoSQL, просто есть ассоциативное хранилище данных, которое может представить всё самым простым возможным способом. И данные всегда находятся в наиболее близкой к оригиналу форме.

Математическое введение в Теорию Связей

Введение

А теперь, когда мы кратко познакомили читателя с чего всё начиналось, настала пора погрузиться в теорию ещё глубже.

Теория связей разрабатывается как более фундаментальная теория по сравнению с теорией множеств и теорий типов и на замену реляционной алгебре и теории графов. В то время, как в Теории Типов основными понятиями являются «тип» и «значение», а в Теории Множеств — «множество», «значение», В Теории Связей все сводиться к единому понятию «связь».

В этом разделе мы разберем основные понятия и термины, используемые в теории связей.

Затем перейдем к определениям теории связей в рамках теории множеств, которое мы отразим на теорию типов используя интерактивное программное средство доказательства теорем «Coq».

В заключении будут подведены итоги и представлены направления дальнейшего исследования и развития теории cвязей.

Теория связей

В основе всей теории связей лежит единое понятие связи. Дополнительное понятие ссылки на связь требуется вводить только для теорий которые не поддерживают рекурсивность определения, такие как теория множеств и теория типов.

Связь

Связь имеет ассиметричную рекурсивную структуру, которая может быть выражена просто: связь связывает связи. Под ассиметричностью имеется ввиду то, что каждая связь имеет направление от источника (начала) к приёмнику (концу).

Определения Теории связей в рамках Теории множеств

Ссылка на вектор — уникальный идентификатор или порядковый номер, каждый из которых связан с определенным вектором представляющим последовательность ссылок на другие вектора.
Множество ссылок на вектора: L ⊆ ℕ₀.

Вектор ссылок — это вектор, состоящий из нуля или нескольких ссылок на вектора, где количество ссылок соответствует количеству элементов вектора.
Множество всех векторов ссылок длины n ∈ ℕ₀: Vn = Lⁿ.
Декартова степень Lⁿ всегда даст вектор длины n, так как все его компоненты будут одного и того же типа L.
Другими словами, Lⁿ представляет собой множество всех возможных n-элементных векторов, где каждый элемент вектора принадлежит последовательности L. Это эквивалентно по сути n-кортежу.

Ассоциация — это упорядоченная пара, состоящая из ссылки на вектор и вектора ссылок.
Эта структура служит для отображения между ссылками и векторами.
Множество всех ассоциаций: A = L × Vn.

Семейство функций: ∪_f {anetvⁿ | n ∈ ℕ₀} ⊆ A.
Здесь ∪ обозначает объединение всех функций в семействе {anetvⁿ}, ⊆ обозначает 'это подмножество', а A — множество всех ассоциаций.
Это говорит о том, что все упорядоченные пары, функций anetvⁿ, представленных в виде функционального бинарного отношения, являются подмножеством A.

Ассоциативная сеть векторов длины n (или n-мерная асеть) из семейства функций {anetvⁿ}, anetvⁿ : L → Vn отображает ссылку R из множества L в вектор ссылок длины n, который принадлежит множеству Vn, фактически идентифицирует точки в n-мерном пространстве.
'n' в anetvⁿ указывает на то, что функция возвращает вектора, содержащие n ссылок.
Каждая n-мерная ассоциативная сеть таким образом представляет последовательность точек в n-мерном пространстве.

Дуплет ссылок (упорядоченная пара или двухмерный вектор): D = L²
Это множество всех упорядоченных пар (L, L), или вторая декартова степень L.

Ассоциативная сеть дуплетов (или двумерная асеть): anetd: L → L².
Каждая ассоциативная сеть дуплетов таким образом представляет последовательность точек в двухмерном пространстве.

Пустой вектор представлен пустым множеством: () представляемый как ∅.

Ассоциативная сеть вложенных упорядоченных пар: anetl: L → NP, где NP = {(∅, ∅) | (l, np), l ∈ L, np ∈ NP} — это множество вложенных упорядоченных пар, которое состоит из пустых пар, и пар содержащих один или более элементов. Таким образом длины n ∈ ℕ₀ можно представить как вложенные упорядоченные пары.

Проекция Теории Связей в Теории Типов (Coq) через Теорию Множеств

Про Coq

Coq — это интерактивное средство для создания доказательств, реализующее теорию типов высшего порядка, которая известна также как Язык Калькуляции Индуктивных Построений (Calculus of Inductive Constructions, CIC). Это среда обладает возможностями формализации сложных математических теорем, проверки доказательств на корректность, а также извлечения работающего программного кода из формально проверенных спецификаций. Coq широко используется в академических кругах для формализации математики, а также в IT-индустрии для верификации программного обеспечения и оборудования.

Решение применить Coq для описания теории связей в рамках теории типов было обусловлено необходимостью строгой формализации доказательств и гарантирования верности логических построений в рамках разработки теории связей. Использование Coq позволяет выразить свойства и операции над связями в точных и надёжных терминах, благодаря системе типов Coq и мощным средствам для создания и проверки доказательств.

В преддверии обширной работы по доказательству эквивалентности реляционной модели и ассоциативной сети дуплетов, мы представляем в этом разделе начальные шаги выполненные с использованием системы доказательств языка Coq. На первом этапе стоит задача формализации структур ассоциативных сетей через определения базовых типов функций и структур внутри Coq.

Определения ассоциативных сетей

(* Последовательность ссылок на вектора: L ⊆ ℕ₀ *)
Definition L := nat.

(* Дефолтное значение L: ноль *)
Definition LDefault : L := 0.

(* Множество векторов ссылок длины n ∈ ℕ₀: Vn ⊆ Lⁿ *)
Definition Vn (n : nat) := t L n.

(* Дефолтное значение Vn *)
Definition VnDefault (n : nat) : Vn n := Vector.const LDefault n.

(* Множество всех ассоциаций: A = L × Vn *)
Definition A (n : nat) := prod L (Vn n).

(* Ассоциативная сеть векторов длины n (или n-мерная асеть) из семейства функций {anetvⁿ : L → Vn} *)
Definition ANetVf (n : nat) := L -> Vn n.

(* Ассоциативная сеть векторов длины n (или n-мерная асеть) в виде последовательности *)
Definition ANetVl (n : nat) := list (Vn n).

(* Вложенные упорядоченные пары *)
Definition NP := list L.

(* Ассоциативная сеть вложенных упорядоченных пар: anetl : L → NP *)
Definition ANetLf := L -> NP.

(* Ассоциативная сеть вложенных упорядоченных пар в виде последовательности вложенных упорядоченных пар *)
Definition ANetLl := list NP.

(* Дуплет ссылок *)
Definition D := prod L L.

(* Дефолтное значение D: пара из двух LDefault, используется для обозначения пустого дуплета *)
Definition DDefault : D := (LDefault, LDefault).

(* Ассоциативная сеть дуплетов (или двумерная асеть): anetd : L → L² *)
Definition ANetDf := L -> D.

(* Ассоциативная сеть дуплетов (или двумерная асеть) в виде последовательности дуплетов *)
Definition ANetDl := list D.

Леммы ассоциативных сетей

(* Функция преобразования Vn в NP *)
Fixpoint VnToNP {n : nat} (v : Vn n) : NP :=
  match v with
  | Vector.nil _ => List.nil
  | Vector.cons _ h _ t => List.cons h (VnToNP t)
  end.

(* Функция преобразования ANetVf в ANetLf *)
Definition ANetVfToANetLf {n : nat} (a: ANetVf n) : ANetLf:=
  fun id => VnToNP (a id).

(* Функция преобразования ANetVl в ANetLl *)
Definition ANetVlToANetLl {n: nat} (net: ANetVl n) : ANetLl :=
  map VnToNP net.

(* Функция преобразования NP в Vn *)
Fixpoint NPToVnOption (n: nat) (p: NP) : option (Vn n) :=
  match n, p with
  | 0, List.nil => Some (Vector.nil nat)
  | S n', List.cons f p' => 
      match NPToVnOption n' p' with
      | None => None
      | Some t => Some (Vector.cons nat f n' t)
      end
  | _, _ => None
  end.

(* Функция преобразования NP в Vn с VnDefault *)
Definition NPToVn (n: nat) (p: NP) : Vn n :=
  match NPToVnOption n p with
  | None => VnDefault n
  | Some t => t
  end.

(* Функция преобразования ANetLf в ANetVf *)
Definition ANetLfToANetVf { n: nat } (net: ANetLf) : ANetVf n :=
  fun id => match NPToVnOption n (net id) with
            | Some t => t
            | None => VnDefault n
            end.

(* Функция преобразования ANetLl в ANetVl *)
Definition ANetLlToANetVl {n: nat} (net : ANetLl) : ANetVl n :=
  map (NPToVn n) net.

(* Определение anets_equiv вводит предикат эквивалентности двух ассоциативных сетей векторов длины n,
 anet1 и anet2 типа ANetVf. 

  Данный предикат описывает свойство "эквивалентности" для таких сетей.
 Он утверждает, что anet1 и anet2 считаются "эквивалентными", если для каждой ссылки id вектор,
 связанный с id в anet1, точно совпадает с вектором, связанным с тем же id в anet2.
*)
Definition ANetVf_equiv {n: nat} (anet1: ANetVf n) (anet2: ANetVf n) : Prop :=
  forall id, anet1 id = anet2 id.

(* Определение anets_equiv вводит предикат эквивалентности двух ассоциативных сетей векторов длины n,
 anet1 и anet2 типа ANetVl.
*)
Definition ANetVl_equiv_Vl {n: nat} (anet1: ANetVl n) (anet2: ANetVl n) : Prop :=
  anet1 = anet2.

(*  Доказательства *)

(* Лемма о сохранении длины векторов ассоциативной сети *)
Lemma Vn_dim_preserved : forall {l: nat} (t: Vn l), List.length (VnToNP t) = l.
Proof.
  intros l t.
  induction t.
  - simpl. reflexivity.
  - simpl. rewrite IHt. reflexivity.
Qed.

(* Лемма о взаимном обращении функций NPToVnOption и VnToNP

  H_inverse доказывает, что каждый вектор Vn без потери данных может быть преобразован в NP
 с помощью VnToNP и обратно в Vn с помощью NPToVnOption.

  В формальном виде forall n: nat, forall t: Vn n, NPToVnOption n (VnToNP t) = Some t говорит о том,
 что для всякого натурального числа n и каждого вектора Vn длины n,
 мы можем преобразовать Vn в NP с помощью VnToNP,
 затем обратно преобразовать результат в Vn с помощью NPToVnOption n,
 и в итоге получать тот же вектор Vn, что и в начале.

  Это свойство очень важно, потому что оно гарантирует,
 что эти две функции образуют обратные друг к другу пары функций на преобразуемом круге векторов Vn и NP.
 Когда вы применяете обе функции к значениям в преобразуемом круге, вы в итоге получаете исходное значение.
 Это означает, что никакая информация не теряется при преобразованиях,
 так что можно свободно конвертировать между Vn и NP,
 если это требуется в реализации или доказательствах.
 *)
Lemma H_inverse: forall n: nat, forall t: Vn n, NPToVnOption n (VnToNP t) = Some t.
Proof.
  intros n.
  induction t as [| h n' t' IH].
  - simpl. reflexivity.
  - simpl. rewrite IH. reflexivity.
Qed.

(*
  Теорема обертывания и восстановления ассоциативной сети векторов:

Пусть дана ассоциативная сеть векторов длины n, обозначенная как anetvⁿ : L → Vⁿ.
Определим операцию отображения этой сети в ассоциативную сеть вложенных упорядоченных пар anetl : L → NP,
  где NP = {(∅,∅) | (l,np), l ∈ L, np ∈ NP}.
Затем определим обратное отображение из ассоциативной сети вложенных упорядоченных пар обратно в ассоциативную сеть векторов длины n.

  Теорема утверждает:

Для любой ассоциативной сети векторов длины n, anetvⁿ, применение операции преобразования в ассоциативную сеть вложенных упорядоченных пар
 и обратное преобразование обратно в ассоциативную сеть векторов длины n обеспечивает восстановление исходной сети anetvⁿ.
То есть, если мы преобразуем anetvⁿ в anetl и потом обратно в anetvⁿ, то мы получим исходную ассоциативную сеть векторов anetvⁿ.
 Иначе говоря:

    ∀ anetvⁿ : L → Vⁿ, преобразованиеобратно(преобразованиевперед(anetvⁿ)) = anetvⁿ.
*)

Theorem anetf_equiv_after_transforms : forall {n: nat} (anet: ANetVf n),
  ANetVf_equiv anet (fun id => match NPToVnOption n ((ANetVfToANetLf anet) id) with
                            | Some t => t
                            | None   => anet id
                            end).
Proof.
  intros n net id.
  unfold ANetVfToANetLf.
  simpl.
  rewrite H_inverse.
  reflexivity.
Qed.


(*  Примеры *)

Definition complexExampleNet : ANetVf 3 :=
  fun id => match id with
  | 0 => [0; 0; 0]
  | 1 => [1; 1; 2]
  | 2 => [2; 4; 0]
  | 3 => [3; 0; 5]
  | 4 => [4; 1; 1]
  | S _ => [0; 0; 0]
  end.

Definition exampleTuple0 : Vn 0 := [].
Definition exampleTuple1 : Vn 1 := [0].
Definition exampleTuple4 : Vn 4 := [3; 2; 1; 0].
Definition nestedPair0 := VnToNP exampleTuple0.
Definition nestedPair1 := VnToNP exampleTuple1.
Definition nestedPair4 := VnToNP exampleTuple4.
Check nestedPair0.
Check nestedPair1.
Check nestedPair4.
Compute nestedPair0.
Compute nestedPair1.
Compute nestedPair4.

Compute (ANetVfToANetLf complexExampleNet) 0.
Compute (ANetVfToANetLf complexExampleNet) 1.
Compute (ANetVfToANetLf complexExampleNet) 2.
Compute (ANetVfToANetLf complexExampleNet) 3.
Compute (ANetVfToANetLf complexExampleNet) 4.
Compute (ANetVfToANetLf complexExampleNet) 5.

Definition testPairsNet : ANetLf :=
  fun _ => cons 1 (cons 2 (cons 0 nil)).

Definition testTuplesNet : ANetVf 3 :=
  ANetLfToANetVf testPairsNet.

Compute testTuplesNet 0.

(* Предикат эквивалентности для ассоциативных сетей дуплетов ANetDf *)
Definition ANetDf_equiv (anet1: ANetDf) (anet2: ANetDf) : Prop := forall id, anet1 id = anet2 id.

(* Предикат эквивалентности для ассоциативных сетей дуплетов ANetDl *)
Definition ANetDl_equiv (anet1: ANetDl) (anet2: ANetDl) : Prop := anet1 = anet2.

(* Функция преобразования NP в ANetDl со смещением индексации *)
Fixpoint NPToANetDl_ (offset: nat) (np: NP) : ANetDl :=
  match np with
  | nil => nil
  | cons h nil => cons (h, offset) nil
  | cons h t => cons (h, S offset) (NPToANetDl_ (S offset) t)
  end.

(* Функция преобразования NP в ANetDl*)
Definition NPToANetDl (np: NP) : ANetDl := NPToANetDl_ 0 np.

(* Функция добавления NP в хвост ANetDl *)
Definition AddNPToANetDl (anet: ANetDl) (np: NP) : ANetDl :=
  app anet (NPToANetDl_ (length anet) np).

(* Функция отрезает голову anetd и возвращает хвост начиная с offset  *)
Fixpoint ANetDl_behead (anet: ANetDl) (offset : nat) : ANetDl :=
  match offset with
  | 0 => anet
  | S n' =>
    match anet with
    | nil => nil
    | cons h t => ANetDl_behead t n'
    end
  end.

(* Функция преобразования ANetDl в NP с индексации в начале ANetDl начиная с offset*)
Fixpoint ANetDlToNP_ (anet: ANetDl) (offset: nat) (index: nat): NP :=
  match anet with
  | nil => nil
  | cons (x, next_index) tail_anet =>
    if offset =? index then
      cons x (ANetDlToNP_ tail_anet (S offset) next_index)
    else
      ANetDlToNP_ tail_anet (S offset) index
  end.

(* Функция чтения NP из ANetDl по индексу дуплета*)
Definition ANetDl_readNP (anet: ANetDl) (index: nat) : NP :=
  ANetDlToNP_ anet 0 index.

(* Функция преобразования ANetDl в NP начиная с головы списка асети *)  
Definition ANetDlToNP (anet: ANetDl) : NP := ANetDl_readNP anet 0.


(*  Доказательства *)

(* Лемма о сохранении длины списков NP в ассоциативной сети дуплетов *)
Lemma NP_dim_preserved : forall (offset: nat) (np: NP), 
    length np = length (NPToANetDl_ offset np).
Proof.
  intros offset np.
  generalize dependent offset. 
  induction np as [| n np' IHnp']; intros offset.
  - simpl. reflexivity.
  - destruct np' as [| m np'']; simpl; simpl in IHnp'.
    + reflexivity.
    + rewrite IHnp' with (offset := S offset). reflexivity.
Qed.


(* Лемма о взаимном обращении функций NPToANetDl и ANetDlToNP

  H_inverse доказывает, что каждый список NP без потери данных может быть преобразован в ANetDl
 с помощью NPToANetDl и обратно в NP с помощью ANetDlToNP.

  В формальном виде forall (np: NP), ANetDlToNP (NPToANetDl np) = np говорит о том,
 что для всякого список NP, мы можем преобразовать NP в ANetDl с помощью NPToANetDl,
 затем обратно преобразовать результат в NP с помощью ANetDlToNP,
 и в итоге получать тот же список NP, что и в начале.

  Это свойство очень важно, потому что оно гарантирует,
 что эти две функции образуют обратные друг к другу пары функций на преобразуемом круге списоке NP и ANetDl.
 Когда вы применяете обе функции к значениям в преобразуемом круге, вы в итоге получаете исходное значение.
 Это означает, что никакая информация не теряется при преобразованиях,
 так что вы можете свободно конвертировать списком NP и ANetDl,
 если это требуется в вашей реализации или доказательствах.
 
Theorem NP_ANetDl_NP_inverse: forall (np: NP),
  ANetDlToNP_ (NPToANetDl np) (length np) = np.
Proof.
  intros np.
  induction np as [| h t IH].
  - reflexivity.
  - simpl. 
    case_eq t; intros.  
    + reflexivity. 
    + simpl.
      rewrite NP_dim_preserved. 
      rewrite H in IH.
      reflexivity.
Qed.
*)

Notation "{ }" := (nil) (at level 0).
Notation "{ x , .. , y }" := (cons x .. (cons y nil) ..) (at level 0).

Примеры применения лемм

(*  Примеры *)

Compute NPToANetDl { 121, 21, 1343 }.
(* Должно вернуть: {(121, 1), (21, 2), (1343, 2)} *)

Compute AddNPToANetDl {(121, 1), (21, 2), (1343, 2)} {12, 23, 34}. 
(* Ожидается результат: {(121, 1), (21, 2), (1343, 2), (12, 4), (23, 5), (34, 5)} *)


Compute ANetDlToNP {(121, 1), (21, 2), (1343, 2)}. 
(* Ожидается результат: {121, 21, 1343} *)

Compute ANetDlToNP {(121, 1), (21, 2), (1343, 2), (12, 4), (23, 5), (34, 5)}. 
(* Ожидается результат: {121, 21, 1343} *)

Compute ANetDl_readNP {(121, 1), (21, 2), (1343, 2), (12, 4), (23, 5), (34, 5)} 0.
(* Ожидается результат: {121, 21, 1343} *)

Compute ANetDl_readNP {(121, 1), (21, 2), (1343, 2), (12, 4), (23, 5), (34, 5)} 3.
(* Ожидается результат: {12, 23, 34} *)


(*
  Теперь всё готово для преобразования асети вложенных упорядоченных пар anetl : L → NP
в асеть дуплетов anetd : L → L².

Данное преобразование можно делать по разному: с сохранением исходных ссылок на вектора
либо с переиндексацией. Переиндексацию можно не делать если написать дополнительную функцию для
асети дуплетов которая возвращает вложенную упорядоченную пару по её ссылке.
*)

(* Функция добавления ANetLl в ANetDl *)
Fixpoint AddANetLlToANetDl (anetd: ANetDl) (anetl: ANetLl) : ANetDl :=
  match anetl with
  | nil => anetd
  | cons h t => AddANetLlToANetDl (AddNPToANetDl anetd h) t
  end.

(* Функция преобразования ANetLl в ANetDl *)
Definition ANetLlToANetDl (anetl: ANetLl) : ANetDl :=
  match anetl with
  | nil => nil
  | cons h t => AddANetLlToANetDl (NPToANetDl h) t
  end.


(* Функция поиска NP в хвосте ANetDl начинающемуся с offset по её порядковому номеру. Возвращает offset NP *)
Fixpoint ANetDl_offsetNP_ (anet: ANetDl) (offset: nat) (index: nat) : nat :=
  match anet with
  | nil => offset + (length anet)
  | cons (_, next_index) tail_anet =>
    match index with
    | O => offset
    | S index' => 
      if offset =? next_index then
        ANetDl_offsetNP_ tail_anet (S offset) index'
      else
        ANetDl_offsetNP_ tail_anet (S offset) index
    end
  end.


(* Функция поиска NP в ANetDl по её порядковому номеру. Возвращает offset NP *)
Definition ANetDl_offsetNP (anet: ANetDl) (index: nat) : nat :=
  ANetDl_offsetNP_ anet 0 index.

(* Функция преобразования ANetVl в ANetDl *)
Definition ANetVlToANetDl {n : nat} (anetv: ANetVl n) : ANetDl :=
  ANetLlToANetDl (ANetVlToANetLl anetv).


(*
  Теперь всё готово для преобразования асети дуплетов anetd : L → L²
 в асеть вложенных упорядоченных пар anetl : L → NP

Данное преобразование будем делать с сохранением исходных ссылоке на вектора.
Переиндексацию можно не делать, потому что есть функция ANetDl_offsetNP для
асети дуплетов которая возвращает смещение вложенной УП по ссылке на её.
*)

(* Функция отрезает первую NP из ANetDl и возвращает хвост *)
Fixpoint ANetDl_beheadNP (anet: ANetDl) (offset: nat) : ANetDl :=
  match anet with
  | nil => nil
  | cons (_, next_index) tail_anet =>
    if offset =? next_index then (* конец NP *)
      tail_anet
    else  (* ещё не конец NP *)
      ANetDl_beheadNP tail_anet (S offset)
  end.

(* Функция преобразования NP и ANetDl со смещения offset в ANetLl *)
Fixpoint ANetDlToANetLl_ (anetd: ANetDl) (np: NP) (offset: nat) : ANetLl :=
  match anetd with
  | nil => nil (* отбрасываем NP даже если она недостроена *)
  | cons (x, next_index) tail_anet =>
    if offset =? next_index then (* конец NP, переходим к следующей NP *)
      cons (app np (cons x nil)) (ANetDlToANetLl_ tail_anet nil (S offset))
    else  (* ещё не конец NP, парсим асеть дуплетов дальше *)
      ANetDlToANetLl_ tail_anet (app np (cons x nil)) (S offset)
  end.


(* Функция преобразования ANetDl в ANetLl *)
Definition ANetDlToANetLl (anetd: ANetDl) : ANetLl :=
  ANetDlToANetLl_ anetd nil LDefault.


(*  Примеры *)

Definition test_anetl := { {121, 21, 1343}, {12, 23}, {34}, {121, 21, 1343}, {12, 23}, {34} }.
Definition test_anetd := ANetLlToANetDl test_anetl.

Compute test_anetd.
(* Ожидается результат:
 {(121, 1), (21, 2), (1343, 2),
  (12, 4), (23, 4),
  (34, 5),
  (121, 7), (21, 8), (1343, 8),
  (12, 10), (23, 10),
  (34, 11)} *)


Compute ANetDl_offsetNP test_anetd 0.
Compute ANetDl_offsetNP test_anetd 1.
Compute ANetDl_offsetNP test_anetd 2.
Compute ANetDl_offsetNP test_anetd 3.
Compute ANetDl_offsetNP test_anetd 4.
Compute ANetDl_offsetNP test_anetd 5.
Compute ANetDl_offsetNP test_anetd 6.
Compute ANetDl_offsetNP test_anetd 7.

Definition test_anetv : ANetVl 3 :=
  { [0; 0; 0], [1; 1; 2], [2; 4; 0], [3; 0; 5], [4; 1; 1], [0; 0; 0] }.

Compute ANetVlToANetDl test_anetv.

Compute test_anetd.
(* Ожидается результат:
 {(121, 1), (21, 2), (1343, 2),
  (12, 4), (23, 4),
  (34, 5),
  (121, 7), (21, 8), (1343, 8),
  (12, 10), (23, 10),
  (34, 11)} *)

Compute ANetDlToANetLl test_anetd.

Definition test_anetdl : ANetDl := ANetVlToANetDl test_anetv.

Definition result_TuplesNet : ANetVl 3 :=
  ANetLlToANetVl (ANetDlToANetLl test_anetdl).

Compute result_TuplesNet.

Практическая реализация

Существует несколько практических реализаций: Deep, LinksPlatform и Модель Отношений.

Deep — это система, основанная на теории связей. В теории связей с помощью связей можно представлять любые данные или знания, а также использовать их для программирования. На это ориентирован Deep. В Deep всё связи. Однако если разделить их на две категории, то у нас будут собственно данные и поведение. Поведение, представленное код в Deep хранится в ассоциативном хранилище в виде связей, а для исполнения передаётся в docker соответствующего языка программирования и изолированно и безопасно выполняется. Вся коммуникация между различными частями кода осуществляется через связи в хранилище (базы данных), что делает базу данных универсальным API основанном на данных (в отличии от традиционной практике вызова функций и методов). В данный момент в качестве ассоциативного хранилища в Deep используется PostgreSQL, который позднее будет заменён на движок данных основанный на дуплетах и триплетах из LinksPlatform.

Deep позволяет делать весь софт на планете совместимым, представляя все его части в виде связей. Также возможно хранить любые данные и код вместе, связывать события действий над различными типами ассоциаций с соответствующим кодом, который выполняется для обработки этих событий. Каждый обработчик может получать необходимые связи из ассоциативного хранилища и вставлять/обновлять/удалять связи в него, что может инициировать дальнейшее каскадное выполнение обработчиков.

Таблица links в базе данных (PostgreSQL) Deep содержит записи, которые можно интерпретировать как связи. Они имеют такие колонки как id, type_id, from_id, и to_id. Типы связей помогают разработчику ассоциативных пакетов предопределить семантику отношений между различными элементами. Что гарантирует однозначное понимание связей как людьми так и кодом в ассоциативных пакетах. Кроме таблицы links, в системе также присутствуют таблицы numbers, strings и objects для хранения числовых, строковых и JSON значений соответственно. К каждой связи можно привязать только одно значение.

LinksPlatfrom — это кроссплатформенный мультиязычный фреймворк который направлен на то, чтобы осуществить низкоуровневую реализацию ассоциативности в виде конструктора движков баз данных. К примеру, на текущий момент у нас существует бенчмарк, который сравнивает реализацию дуплетов в PostgreSQL и аналогичную реализацию на чистом Rust/C++, лидирующая реализация на Rust обгоняет PostgreSQL на операциях записи в 200+ раз, а на операциях чтения в 1000+ раз.

Заключение

Планы на будущее

В данной статье была продемонстрирована лишь малая часть всех наработок по теории связей, которые накопились за несколько лет работы и исследований. В следующий статьях постепенно будут раскрыты и другие проекции теории связи, в терминах иных теорий, таких как: реляционная алгебра, теория графов, а также рассмотрение в терминах теории типов без использования теории множеств на основе ассоциативных чисел (кодовое название), и разбор отличий от ассоциативной модели данных Саймона Вильямса.
Ещё планируется демонстрация четкой и общей терминологии теории связей, ее основных постулатов, аспектов, ассоциативных корней. Текущий прогресс по разработке теории можно наблюдать в репозитории deep-theory.

Чтобы не пропустить обновления, рекомендуем подписаться на блог Deep.Foundation здесь или уже сейчас посмотреть наши наработки на GitHub или напрямую написать нам на нашем сервере в Discord (особенно подойдёт, если вы боитесь что вас заминусуют в комментариях).

Будем рады любой вашей обратной связи что здесь на хабре, что на GitHub и Discord.

P.S. Статья будет обновляться по мере развития и дополнения Теории Связи в течение следующего месяца.

Ссылки

1. «Relational Model of Data for Large Shared Data Banks.», paragraph 1.3., Edgar F. Codd, IBM Research Laboratory, San Jose, California, June 1970