[Перевод] Сила известных физических взаимодействий
В этой статье я хочу обсудить основные свойства известных нам взаимодействий — четырёх наблюдаемых и пятого — нового — о чьём существовании мы делаем вывод из открытия частицы Хиггса.
Конкретно я хочу обсудить, что имеют в виду специалисты по физике частиц, описывая взаимодействия, как слабые или сильные. Такую терминологию вы можете встречать часто, но если её никто вам не объяснял, невозможно догадаться, что она означает. Так что вот вам объяснение — хоть и длинное, но, надеюсь, оно откроет вам глаза на то, как работает природа, а также поднимет много новых вопросов, на которые я надеюсь ответить позже.
«Слабые» против «сильных»
Что означают эти термины? В обычной жизни мы представляли бы, что сильное взаимодействие может поднять нас в воздух, а со слабым мы можем справиться, немного напрягши мускулы. Но специалисты по физике частиц имеют в виду вовсе не это.
Говоря о сильных и слабых, физики не имеют в виду абсолютную силу или слабость взаимодействия. Речь не идёт о том, сможет ли взаимодействие разбить окно или удержать золотой слиток. В этом контексте термины «сильный» и «слабый» не совсем абсолютные, в том смысле, в котором мы используем их в повседневной жизни или даже в начальных классах по физике. Эта терминология появилась благодаря глубокому пониманию квантовой теории поля, современного математического языка, используемого для описания известных элементарных частиц и сил. Но он фундаментален для современного обсуждения этих проблем физиками. Так что я начну с обоснования причин появления таких терминов.
Возьмём пару объектов определённого типа, допустим, элементарных частиц, и поместим их на расстоянии r друг от друга. Допустим, каждая оказывает воздействие F на другую. Тогда мы скажем, что воздействие слабое, если
Где h — постоянная Планка, c — скорость света. Часто в физике удобно использовать не h, а
Короче говоря, в физике частиц:
• Для слабого взаимодействия
• Для сильного взаимодействия
Обычно, даже в теоретических изысканиях, нам не встречаются взаимодействия гораздо сильнее . Такая сила делает их столь сложными, что мы работаем с ними иным способом. Но это долгая история.
Получается, что подобная характеристика говорит не об абсолютной силе или слабости взаимодействия, но о том, является ли оно сильным или слабым по сравнению с типичными взаимодействиями, работающими на расстоянии r. Учитывается не само взаимодействие; учитывается взаимодействие, помноженное на квадрат расстояния, и эта величина сравнивается с ℏ c.
Чтобы объяснить полезность этого понятия, я дам иллюстрацию для случая электромагнитных взаимодействий, воздействующих на простые заряженные частицы — электроны, позитроны и протоны. Электрический заряд электронов равен –e; у протонов и позитронов заряд равен +e.
Во-первых, представьте два неподвижных протона, каждый массой m и электрическим зарядом +e, находящихся на расстоянии r друг от друга. Электрическая сила расталкивает их в стороны, и её величина задаётся формулой
Та же формула применима и для двух электронов с зарядом –e. Для электрона и позитрона взаимодействие будет таким же, только оно будет притягивать их, а не расталкивать.
Что такое k? Это постоянная Кулона, а её значение зависит от того, как определять e, основную единицу заряда. Но это неважно, поскольку при обсуждении электрических взаимодействий и элементарных частиц мы всегда будем видеть совместное появление ke2. Нам не нужно знать, насколько велика k, нам только нужно знать, насколько велика ke2?
Оказывается, что если r больше, чем миллионная миллионной доли метра, тогда ke2 примерно равняется 0,007, помножить на (h c/2π), где h — постоянная Планка, а c — скорость света. Поэтому мы можем записать электрическую силу, помноженную на r2, как примерно равную
Поскольку 0,007 гораздо меньше 1, электромагнетизм — слабое взаимодействие, и остаётся таким на всех расстояниях, измеренных нами.
Тут очень важно не запутаться! Только из того, что электромагнетизм — слабое взаимодействие, не следует, что взаимодействие двух протонов слабое в абсолютном исчислении. На самом деле электрическую силу, пытающуюся оттолкнуть два протона в ядре гелия, можно сравнить с весом грузовика! И вся эта сила действует на две крохотных частички! Но для таких малых расстояний это воздействие довольно слабое, и более сильное взаимодействие («сильное ядерное взаимодействие») противостоит электромагнитному отталкиванию, удерживая протоны и нейтроны в ядре гелия вместе.
Кстати, для этой величины 0,007 есть историческое название; её называют постоянной тонкой структуры (поскольку она задаёт размер небольших отличий в энергиях различных конфигураций атомов), и обычно обозначают α:
Это одна из наиболее точно измеренных величин природы. Часто люди записывают её примерно равной 1/137 (и многие годы некоторые учёные думали, что число 137 какое-то особенное), но если делать это совсем точно, тогда придётся записать 1/137,0359990…
Так почему же тот факт, что α гораздо меньше 1, говорит о том, что это взаимодействие надо записать в слабые, а не в сильные?
Почему то, что α << 1, означает, что электромагнитное взаимодействие слабое
Проще всего показать это на примере, в котором сила притягивает частицы — например, электрон и позитрон, или электрон и протон. С электрона и позитрона начать легче, поскольку у них равные массы; они формируют похожее на атом состояние под названием позитроний, аналогичное атому водорода, сформированному электроном и протоном, но более симметричное, в котором две частицы движутся по орбите друг вокруг друга. В атоме водорода электрон движется по орбите вокруг практически неподвижного протона. На самом деле формулы для водорода подходят и для позитрония, с небольшими изменениями (отличаются в 2 раза) в нескольких местах. (Да, электрон и позитрон в позитронии в конце концов аннигилируют и превращаются в два-три фотона, но только после того, как частицы совершат много миллиардов оборотов — что, правда, занимает малую долю секунды). Для позитрония в состоянии наименьшей энергии:
• типичная скорость каждой частицы равна α/2 × c;
• типична энергия движения (кинетическая) каждой частицы равна mc2 × α2/8;
энергия взаимодействия (потенциальная) двух частиц равна –mc2 × α2/2;
• связывающая энергия B позитрониума (сумма энергии движения и энергии взаимодействия) равна mc2 × α2/4;
• энергия массы позитрониума 2 mc2 — B; и поскольку второе гораздо меньше первого, то масса атома оказывается всего лишь немногим меньшей, чем сумма масс электрона и позитрона.
Короче говоря, из-за того, что α гораздо меньше 1, существуют три важнейших, связанных между собой факта:
• Электрон и позитрон двигаются со скоростями, сравнимыми со скоростью света c.
• Кинетическая энергия, потенциальная энергия и энергия связи B малы по сравнению с энергией массы электрона и позитрона, E = mc2.
• Масса позитрония очень близка к сумме масс электрона и позитрона.
Все эти утверждения верны вне зависимости от того, насколько велика или мала масса электрона; они зависят только от малой величины α.
Всё это вместе значит, что для описания этого похожего на атом состояния Эйнштейновская специальная теория относительности не важна. Законы движения Ньютона достаточно хорошо подходят для предсказаний, вплоть до деталей, не больших, чем α — то есть, с точностью в 1% или лучше. И, как мы увидим далее, это значит, что система относительно проста. Её можно описать, используя квантовую механику с достаточно простой математикой, без участия квантовой теории поля, которая была бы необходима, если бы была важна СТО. Математика атома водорода такая же, как у позитрониума, и она настолько простая, что физики знакомятся с ней в институте, на первых уроках по квантовой механике.
Об этом можно думать ещё одним полезным, хотя и менее известным способом. Нужно помнить, что электроны, как и все элементарные частицы, в реальности являются квантами — крохотными возмущениями квантовых полей. Они больше похожи на волны, чем на мелкие шарики. Соответственно, они вибрируют, как и все волны: у них есть частота вибраций. Время, проходящее от одной вибрации до другой — которое я люблю поэтически называть «сердцебиением» — равно hc/m. Если α мало, тогда время, требуемое свету на то, чтобы пересечь атомоподобное состояние, гораздо больше, в 1/α раз, чем сердцебиение частиц, которое оно содержит. В этом смысле позитроний довольно большой. И поскольку сами частицы перемещаются гораздо медленнее света, у частиц на пересечение этого атомоподобного состояния уходит ещё больше времени — что-то в районе 1/α2 сердцебиений.
Когда α мало, другие вещи, которые могли быть более сложными, также упрощаются. К примеру, воздействие позитрона на электрон может заставить электрон превратиться в виртуальный электрон и виртуальный фотон — иногда и ненадолго. (Виртуальные «частицы» не являются частицами; настоящая частица — это хорошо ведущая себя волна квантового поля, а виртуальная — это более общее возмущение этих полей). Но это происходит редко, когда α мало. Ещё реже сам виртуальный фотон возмущается и превращается в виртуальный электрон и позитрон. Поскольку энергию в размере 2mc2, необходимую для получения реальных электрона и позитрона, взять неоткуда (вспомните, что энергии движения и взаимодействий гораздо меньше), виртуальные электрон и позитрон появляются очень редко. То, что виртуальные частицы появляются редко, позволяет говорить о том, что «атом позитрония состоит из электрона и позитрона» — именно так и есть, большую часть времени. Только в очень точных вычислениях требуется быть более осторожным, и помнить, что это не всегда так. То же работает и для атома водорода: это (почти всё время) только один электрон и один протон, удерживаемые простым электрическим взаимодействием.
Что было бы, если бы α была бы примерно равной 1?
Теперь представим, что α постепенно растёт и приближается к 1. Что случится с позитрониумом?
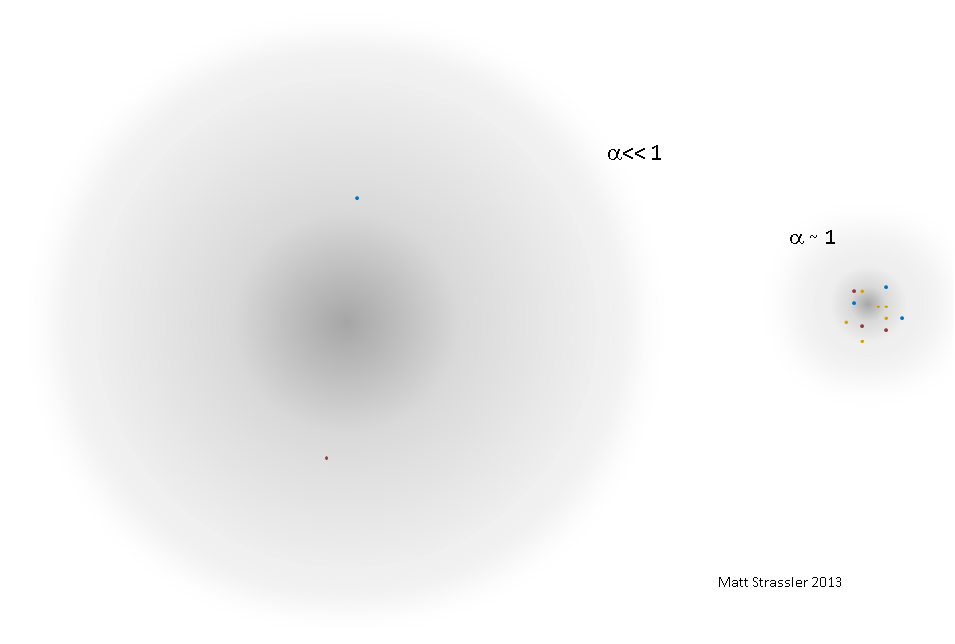
Рис. 1
С увеличением α взаимодействие (на любом расстоянии) между электроном и позитроном становится сильнее, и поскольку они притягиваются сильнее, то частицы в атомоподобном состоянии сдвигаются ближе. Частицы движутся быстрее, приближаясь к скорости света. Энергия движения частиц растёт, величина энергии взаимодействия растёт, как растёт и энергия связи — и приближается к 2m. Соответственно, масса атомоподобного состояния уже не равна примерно 2m. Размер атомоподобного состояния становится меньше; время, требуемое на пересечение его светом, время, требуемое на пересечение его частицами, и время, проходящее между двумя сердцебиениями частиц, начинают сравниваться между собой.
Усиление взаимодействия электрона и позитрона приводит к более частому появлению виртуальных фотонов; присутствие большего количества энергии в атоме облегчает превращение виртуального фотона в виртуальные электрон и позитрон. Когда это происходит, становится трудно сказать, какой электрон реален, а какой виртуален, поскольку между двумя электронами тоже действуют мощные силы, как и между электроном и любым из позитронов. Это может привести к тому, что частица, бывшая реальной, станет виртуальной, и сделает виртуальную частицу реальной — и обратно. А в это время виртуальные электроны и позитроны также могут испускать или поглощать фотоны, которые могут быть и виртуальными, и реальными.
Само разделение между реальными и виртуальными частицами становится сложнее провести. Реальные частицы должны быть правильно ведущими себя возмущениями квантовых полей. Но атомоподобное состояние настолько мало, что у электрона и позитрона на его пересечение уходит всего одно сердцебиение, а в этот момент мощные взаимодействия уже принудят их изменить направление. Как мы можем казать, что такая частица похожа на хорошо себя ведущее возмущение? Хорошо себя ведущая волна должна волноваться некоторое время — несколько сердцебиений — перед тем, как на неё начнут оказывать влияние внешние силы. А тут наш электрон, хотя он и больше похож на реальную частицу, чем на виртуальную, всё же сильно искажается, и уже не подходит под определение «реальной частицы». И этот электрон вообще может существовать недолго. За появлением виртуальной электрон-позитронной пары может последовать аннигиляция бывшего реального электрона с новообразованным позитроном, после чего останется возможно реальный/возможно виртуальный электрон.
Так что, вместо того, что у нас есть малое α — простая система с массой чуть меньше 2m, состоящая из электрона и позитрона, движущихся со скоростями гораздо меньше световой — при приближении α к 1 мы обнаруживаем чрезвычайно сложную систему, в которой множество частиц движется с околосветовыми скоростями, с массой, сильно отличающейся от 2m (см. рис. 1). Невозможно сказать, сколько частиц находится внутри — будем ли мы считать только реальные? Если да, каким образом точно отличить почти реальные от почти виртуальных? Количество реальных частиц может постоянно меняться.
Вот, что характеризует реально сильное взаимодействие; формируемые им объекты гораздо сложнее атомов. Учёным в каком-то смысле повезло, что первыми объектами, встреченными на пути к квантовой теории поля, были атомы. Их удерживает слабое взаимодействие — электромагнитная сила — и их было легко понять при помощи простой математики квантовой механики, в которой количество частиц постоянно. Протоны же удерживает сильное взаимодействие — сильное ядерное взаимодействие. Поэтому неудивительно, что строение протонов гораздо, гораздо сложнее, чем у атомов. Количество частиц внутри протона постоянно меняется — и для этого требуется гораздо более сложная математика квантовой теории поля.
Кстати, электрическое взаимодействие между двумя электронами слабое из-за того, что α мало. То же самое верно для взаимодействий между двумя элементарными частицами, поскольку заряды всех известных частиц находятся в промежутке от –e до e — к примеру, заряд верхних кварков равен 2/3 e. Вы можете заинтересоваться взаимодействием между электроном и ядром урана, поскольку заряд ядра урана равен 92 e. Да, в этом случае взаимодействие оказывается весьма сильным! Но в этом случае проявляется лишь часть эффектов, описанных мною для сильных взаимодействий, поскольку изменение заряда только одного из взаимодействующих объектов (в частности, тяжёлого) не увеличивает вероятность обнаружения виртуальных электрон-позитронных пар. Это изменится, только если заряд самого электрона станет гораздо больше, чем e! Так что даже атом урана остаётся значительно проще протона.
Насколько слабо слабое ядерное взаимодействие? Сложный вопрос…
Насколько сильны другие известные взаимодействия природы? Мы увидели, что у электрических взаимодействий сила равна α — по крайней мере, на микроскопическом, атомном и субатомном уровне. И на таких расстояниях, вплоть до миллионной миллионных долей метра, α постоянна. Она не зависит от r, и в частности поэтому является такой удобной мерой. Но на самом деле сила взаимодействия может меняться с расстоянием, что всё усложняет. Для электромагнетизма это не так важно, этот эффект очень мал. Но для других сил это важно.
Так называемое слабое ядерное взаимодействие, конечно же, слабое. Оно слабое на макроскопическом, атомном и даже ядерном уровне. Но его сила не постоянна. На расстояниях, больших по сравнению с ℏ c/MW ~ 3 × 10–18 метра (порядка 1/300 радиуса протона), где MW = 80 ГэВ/c2 — масса частицы W, его сила αслабое примерно равна
Экспонента делает это взаимодействие удивительно слабым! Даже на расстояниях, сравнимых с размером протона этот множитель уже равен e-300, что означает уменьшение его силы на столько, что я даже не могу записать тут это число — это 1 со 130 нулями. (Это больше гугола, единицы со ста нулями). И потом эта сила быстро убывает далее. Почему? Тот же эффект, что даёт частице W (возмущению поля W) массу, делает невозможным возмущение поля W на больших расстояниях, в отличие от эффекта, оказываемого электроном или протоном на электрическом поле. Соответственно, воздействие поля W не работает на больших расстояниях.
Но и для ещё меньших расстояний
Обратите внимание, что оно в несколько раз больше, чем электромагнитная сила! Слабое взаимодействие по своей сути вовсе не слабое — см. рис. 2. Предупреждение: я не включаю сюда тонкости, связанные со взаимодействием слабого и электромагнитного взаимодействий на таких малых расстояниях, а также с очень медленным изменением силы, которое становится заметным на куда как меньших дистанциях.
Слабое взаимодействие выглядит таким слабым, при наблюдении его на примере физики ядер, атомов и повседневной жизни, огромная масса частицы W. Если бы частица W не имела массы, то воздействие «слабого» ядерного взаимодействия было бы сильнее, чем у электрического! Это ещё один контекст, в котором поле Хиггса, придающее частице W её массу, играют важную роль в наших жизнях!
Сильное ядерное взаимодействие
Сильное ядерное взаимодействие, притягивающее и отталкивающее кварки и глюоны (но не электроны) работает совсем по-другому. На расстояниях, которые мы обсуждали в случае слабого ядерного взаимодействия — 3 × 10–18 метра — сильное ядерное взаимодействие гораздо сильнее как слабого, так и электромагнитного:
Это не особенно сильно; это примерно в десять раз слабее по-настоящему сильного взаимодействия, и всего в десять раз сильнее электромагнетизма. На самом деле, хотя на макроскопических расстояниях они и сильно отличаются, но сильное ядерное, слабое ядерное и электромагнитное взаимодействие отличаются друг от друга всего примерно в 10 раз на расстояниях меньших, чем 3 × 10–18 м. Это удивительно, и, вероятно, не случайно. Оттуда и до идеи «великого объединения» трёх этих сил шаг совсем небольшой — есть мнение, что на гораздо меньших расстояниях все три взаимодействия обладают одной силой, и становятся частями более универсального взаимодействия.
Но на больших расстояниях сильное ядерное взаимодействие постепенно становится относительно сильным. И опять-таки напоминаю, что мы имеем в виду под «слабым» и «сильным»; взаимодействие становится слабее в абсолютном выражении при увеличении r, но по сравнению, допустим, с электромагнитным взаимодействием на той же дистанции оно становится сильнее.
Это весьма сильно! А к тому времени, как r достигает 10–15 м, радиуса протона, αсильное становится больше 1 и его уже нельзя определить уникальным образом.
Короче, сильное ядерное взаимодействие, которое на расстояниях гораздо меньших радиуса протона демонстрирует умеренную силу, растёт (в относительном понимании) при увеличении расстояний, и становится реально сильным на расстоянии в 10–15 м (это показано на рис. 2). Именно это на самом деле сильное взаимодействие создаёт протон и нейтрон, и остаточный эффект этого взаимодействия комбинирует эти объекты в ядро атома. Другие важные эффекты от усиления этого взаимодействия — преобразование высокоэнергетических кварков и глюонов в адронные струи.
Почему же сильное взаимодействие постепенно растёт при увеличении r? Это я расскажу как-нибудь в другой раз, но по сути, это очень тонкий эффект, возникающий из-за возмущений (виртуальных частиц) в полях кварков и глюонов, на которые воздействует сильное взаимодействие. Такие же эффекты влияют на слабое и электромагнитное взаимодействие, но уже не так сильно, поэтому я его раньше и не упоминал. К примеру, на расстоянии в 3 × 10–18 м электромагнитное α становится ближе к 1/128, чем к его значению для больших расстояний, равное 1/137.
Учитывая силу сильного ядерного взаимодействия, почему же мы не сталкиваемся с ним в повседневной жизни? Это связано с тонкостями того, каким образом оно так плотно упаковывает кварки, глюоны и антикварки в протоны и нейтроны, что мы никогда не наблюдаем их отдельно. Всё это сильно отличается от того, как слабое электромагнитное взаимодействие позволяет электронам легко убегать из атомов, допуская такие явления, как статическое электричество (куда входят и молнии) и электрический ток (в том числе и по проводам).
Сила гравитации
Что насчёт гравитации? Для известных нам частиц гравитация удивительно слаба. Для двух неподвижных частиц массы m гравитация будет иметь величину
Где GN — гравитационная константа Ньютона. Сравните это с электрической силой, у которой α = ke2 / ℏ c. Роли k и e электрических сил здесь играют GN и m. Отмечу, что я использую формулу Ньютона для гравитации, но пока αгравитация мало по сравнению с 1, эйнштейновская формула притяжения двух объектов будет по сути той же.
Теперь перепишем формулу через планковскую массу MP = 1019 ГэВ/с2, или порядка массы 10 миллионов миллионов миллионов протонов, или 20 тысяч миллионов миллионов миллионов электронов. Она равна примерно одной десятой массы крупинки соли.
Так что для двух протонов массой 1 ГэВ/с2 гравитационное взаимодействие между ними будет выражаться квадратом 10–19:
Это единица, перед которой стоит 37 нулей и десятичный разделитель! А для двух электронов
Что, поскольку масса электрона примерно в 2000 раз меньше массы протона, в 4 миллиона раз слабее. Даже для пары верхних кварков, которые почти в 200 раз тяжелее протона, и масса которых наибольшая среди масс всех известных частиц, сила гравитации будет равной
Это примерно в 100 000 000 000 000 000 000 000 000 000 000 раз меньше электрического взаимодействия двух верхних кварков. Поэтому на рис. 2 гравитация не отображена.
Если подумать, эта удивительная слабость гравитации объясняет, почему вы (используя электрические силы, питающие ваши мускулы и удерживающие ваше тело) можете так свободно двигаться, несмотря на то, что вас притягивает целая огромная Земля. Это даже объясняет, как Земля может во столько раз превышать по размерам атом; гравитация хочет сжать Землю, но целостность атомов, чьи электрические силы сопротивляются сжатию, этому мешает. Если бы гравитационные силы были гораздо сильнее, или электрические — слабее, гравитация сжала бы Землю до гораздо меньшего размера и гораздо большей плотности.
Гравитация настолько слаба, что удивительно, что мы её вообще открыли. Почему же она стала первой известной людям силой? Потому, что это единственная сила, выживающая на очень дальних расстояниях в обычной материи.
• Слабое ядерное взаимодействие становится чрезвычайно слабым на больших расстояниях.
• Электромагнетизм выживает дольше, и хотя это взаимодействие не очень сильное, его достаточно для того, чтобы связать большую часть электронов и атомных ядер в электрически нейтральные комбинации, чьи электрически силы взаимно уничтожаются. К примеру, атом водорода не притягивает удалённый электрон, поскольку электрон в атоме водорода отталкивает его, а протон в ядре — притягивает, и две этих силы уравновешиваются.
• Сильное ядерное взаимодействие такое сильное, что связывает кварки, глюоны и антикварки в комбинации, у которых тоже проявляются похожие уравновешивающие эффекты.
• Но уравновешивать гравитацию нечем. Не существует частиц, создающих гравитационное взаимодействие, отталкивающее материю, поэтому нельзя скомбинировать две частицы так, чтобы их гравитационное воздействие на удалённые объекты уравновешивалось.
Взаимодействие Хиггса?
С 2012 года у нас есть новая пища для размышлений: взаимодействие частиц, вызываемое полем Хиггса. Не нужно путать его с эффектом, благодаря которому поле Хиггса придаёт всем известным частицам их массы; поле Хиггса может оказывать этот эффект на единичную, изолированную частицу. Это не воздействие, оно не тянет и не толкает. Но поле Хиггса может также порождать взаимодействие двух частиц; это происходит очень похоже на электромагнетизм. Однако с обычной материей это воздействие очень, очень тяжело обнаружить. На коротких расстояниях для таких частиц, как электроны, и верхние и нижние кварки, доминирующие в протоне, взаимодействие Хиггса очень слабо (слабее, чем электромагнетизм, но гораздо сильнее гравитации). На больших расстояниях, как и слабое ядерное взаимодействие, взаимодействие Хиггса становится чрезвычайно слабым, поскольку у частицы Хиггса, как и у частицы W, есть масса.
Поле Хиггса порождает взаимодействие сходное со слабым ядерным взаимодействием в том, что у него очень малая дистанция воздействия, и что оно становится неэффективным на расстояниях, больших по сравнению с ℏ c / Mh ~ 2 × 10–18 м (1/500 радиуса протона), где Mh ≈ 125 ГэВ/c2, масса частицы Хиггса. На первый взгляд формула похожа на формулу для гравитации, поскольку сила притяжения пропорциональна массам двух элементарных частиц.
Где v = 246 ГэВ, это постоянное значение поля Хиггса, существующее во всей Вселенной. (На самом деле, строго говоря в формуле есть ещё один квадратный корень из 2, но давайте упростим для улучшения понимания).
Но будьте осторожны! Схожесть с гравитацией может сбить с толку. Эта формула точно работает для известных элементарных частиц — объектов, получающих свою массу от поля Хиггса. Она работает для электронов, мюонов и кварков. Она не работает для протонов, нейтронов, атомов или вас! Оттого, что масса протона (и нейтрона, а следовательно, и атома, а следовательно, и ваша) не полностью порождается полем Хиггса. Это отличается от формулы для гравитации, которая верна для всех медленных объектов! Вместо этого в случае обычной атомной материи нам нужно было бы заменить формулу похожей, но имеющей спереди другой множитель, свой для каждого атома. Но качественно зависимость от расстояния осталась бы схожей.
Кроме того, написанная мною формула предполагает существование только одного поля Хиггса и одной частицы Хиггса (что пока ещё не доказано, но является простейшей возможностью, соответствующей полученным данным). Если это не так, формула усложнится, хотя и сохранит схожую форму.
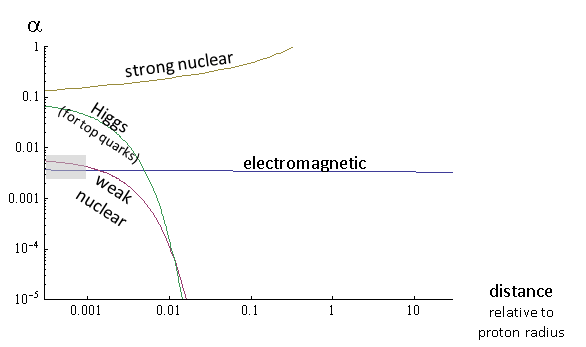
Рис. 2
Насколько сильно это взаимодействие? На очень коротких расстояниях, короче, чем 2 × 10–18 м, взаимодействие Хиггса для двух кварков сравнимо с сильным ядерным взаимодействием на таком же расстоянии (см. рис. 2)! Но в случае электронов, обладающих меньшей массой из-за меньшего взаимодействия с полем Хиггса, это взаимодействие даже на меньших расстояниях будет гораздо слабее электрических — больше, чем в тысячу миллионов раз слабее — хотя и в тысячи миллионов миллионов раз сильнее, чем гравитационное взаимодействие электронов. Однако, если взять два электрона в атоме, которые расположены друг от друга в десять миллионов раз дальше, чем 2 × 10–18 м, тогда взаимодействие Хиггса между ними будет гораздо, гораздо меньше даже крохотного гравитационного взаимодействия, в e10 000 000 раз. И даже если бы поле Хиггса отвечало бы за всю массу протонов и нейтронов, то взаимодействие Хиггса в ядре было бы всё равно гораздо слабее гравитации, которая, в свою очередь, невероятно мала по сравнению с сильным ядерным взаимодействием, удерживающим части ядра.
Именно удивительная слабость взаимодействия Хиггса в контексте обычной материи делает его таким сложным для обнаружения. С другой стороны, взаимодействие Хиггса, как и гравитация, всегда работает на притяжение, и не уравновешивается. Но с третьей стороны, это не имеет значения, поскольку, как и слабое ядерное взаимодействие, взаимодействие Хиггса не выживает на длинных расстояниях, поскольку у частицы Хиггса, как и у частицы W, есть масса. Взаимодействие Хиггса на ультракоротких расстояниях гораздо сильнее гравитации, но на ядерных и атомных расстояниях оно гораздо слабее из-за массы частицы Хиггса. А для частиц малой массы, из которых мы состоим, слабо взаимодействующих с полем Хиггса, взаимодействие Хиггса всегда в тысячи миллионов раз слабее электрических сил, даже очень малых расстояниях.
Так что, хотя каждый атом Земли взаимодействует через Хиггса с каждым другим атомом Земли, эта сила настолько крохотна, даже для соседних атомов, а особенно — для далеко отстоящих, что её эффекта обнаружить невозможно. Поэтому нам пришлось напрямую найти частицу Хиггса, чтобы подтвердить существование поля Хиггса; мы не могли искать создаваемую им силу так, как мы можем наблюдать электрические или магнитные силы и подтверждать таким способом существование электрических и магнитных полей.
Когда же мы сможем наблюдать действие этой силы? Её воздействие будет впервые обнаружено либо при рассеянии частиц W и Z друг с другом (что рано или поздно будет проделано, не напрямую, в столкновениях протонов в Большом адронном коллайдере) или во взаимодействиях верхнего кварка и верхнего антикварка (что можно наблюдать на электрон-позитронном коллайдере — кстати, свою первую работу по физике частиц я написал именно об этом явлении).
