[Перевод] Ричард Хэмминг: Глава 23. Математика
 Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2194 в закладки, 345k прочтений)?
Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2194 в закладки, 345k прочтений)?
Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Давайте ее переведем, ведь мужик дело говорит.
Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»
Мы уже перевели 5 глав.
Глава 23. Математика
(За перевод спасибо Jerry OK, который откликнулся на мой призыв в предыдущей главе».) Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru
В жизни наше внимание в основном приковывают вещи на переднем плане, а окружающий мир воспринимается как данность. Мы считаем само собой разумеющимся воздух, воду и много других вещей, таких как язык и математику. Когда вы работаете в компании долгое время, её структура, методы и обычаи также принимаются как данность.
К таким привычным вещам, которые раньше не привлекали Ваше внимание, стоит время от времени присматриваться, так как большие шаги вперёд часто происходят благодаря таким действиям, и редко без них. По этой причине мы рассмотрим математику, хотя такое же рассмотрение языка тоже может быть плодотворным. Мы используем математику, даже не обсуждая, что это такое. Большинство из нас никогда по-настоящему не задумывалось об этом, мы просто занимались математикой —, но именно она играет главную роль в науке и инженерии.
Пожалуй, «излюбленное» её определение, данное самими математиками, таково:
«Математика — это то, что делается математиками, а математики — это те, кто делает математику.»
Такое определение не только даёт повод для шуток, но также является честным признанием того, что сами учёные не считают, что математика может быть адекватно определена. Существует известная книга «What is Mathematics», авторы которой рассматривают математику со всех сторон, но не пытаются определить её.
Однажды на коктейльной вечеринке глава математического отделения Bell Labs трижды сказал молодой девушке:
«Математика есть не что иное, как чистое мышление».
Сомневаюсь, что собеседница согласилась, но в конце концов она сменила тему; это произвело впечатление на меня. Вы можете также сказать:
«Математика есть не что иное, как язык чистого мышления».
Это не означает, что математика безупречна — вовсе нет — но, похоже, ничего лучше у нас нет. Достаточно только взглянуть на людей, занимающихся правом или подсчётом налогов, и на то, как они используют естественный язык для выражения своих мыслей, чтобы увидеть, как плохо он подходит для чистого мышления. Да что там, простое утверждение «Я лгу» уже противоречит себе!
В мире есть множество естественных языков, но существует только один язык математики. Действительно, есть римская цифра «VII», арабская »7» (разумеется, в латинском начертании, а не арабском), бинарная запись »111», но все они означают одну и ту же мысль в разных представлениях. Семь — это семь, и в любой записи это простое число. Семь как число не нужно путать с его записью.
Большинство людей, серьёзно задумавшихся над вопросом о возможности внеземных контактов, согласно, что, если мы когда-либо свяжемся с цивилизацией далёкой звезды, то у её обитателей будет в сущности та же математика, что и у нас. Слова «в сущности та же» здесь необходимы, потому что, например, их Евклидова геометрия может включать ориентацию, из-за чего для них два треугольника могут быть конгруэнтными или антиконгруэнтными (см. рисунок). Аналогично, Птолемей, рассуждая об астрономии в своём «Альмагесте», использовал обозначение «sin x» там, где мы бы использовали »2*sin (x/2)» (см. рисунок) — в сущности, идея остаётся той же. Отметим, что из предположения наличия связи с ними следует, что они должны развиться до уровня, на котором им известны уравнения Максвелла в том или ином виде. Однако я должен отметить, что некоторые философы сомневаются даже в том, что система связи другой цивилизации будет хоть чем-то похожа на нашу. Но люди, постоянно витающие в облаках, могут вообразить всё, что угодно, и это очень редко будет близко к истине (пример тому — рассуждения о возможном наличии на поверхности Луны многометрового слоя пыли, в котором космический корабль утонет и люди задохнутся).
В течение многих лет развиваются пять основных школ, которые по-своему определяют математику, и ни одно из определений не оказалось полным.
Самая старая из этих школ — платоновская. Пожалуй, именно её взглядов придерживается большинство математиков, когда не задумывается об этом. Платон (427–347 до н.э.) утверждал, что идея стула более реальна, чем любой отдельный стул. Материальные стулья изнашиваются, обдираются, разрушаются и теряются; идеальный стул же неизменяемый, вечный — так он говорил. Следовательно, утверждал он, мир идей более реален, чем материальный мир. Теоремы математики и другие её составляющие принадлежат миру идей (как и утверждал Платон). Наряду с упомянутым выше числом 7, они не встречаются в материальном мире. Вы никогда не видели, не слышали, не трогали и не пробовали абстрактное число 7. Да, вы видели 7 лошадей, 7 коров, 7 стульев, но не число 7 — чистое 7, не загрязнённое конкретной реализацией.
Метафора, которую использовал Платон, заключалась в том, что мы видим реальность только через тени, которые она отбрасывает на стену. Настоящую реальность нельзя увидеть, только её тени доходят до наших чувств. По Платону, наш разум — то, что преодолевает это ограничение и достигает реальных идей.
Вот почему платонистские математики говорят, что они «открыли» результат, а не «создали» его. Если я — платоник, то я «открыл» коды, корректирующие ошибки, а не «создал» их. Результаты всегда были доступны и ждали, что их откроют.
Проблема с платонизмом в том, что он не слишком правдоподобен и определённо не может объяснить то, как математика развивается, не принимая во внимание её развитие и разработку. Основные идеи и определения математики постепенно изменялись с течением столетий, и это не согласуется с представлением о неизменных платоновских идеях. Представление Эйлера (1703–1783) о непрерывности достаточно сильно отличается от того, которому Вас учили. Конечно, можно утверждать, что изменения происходят от того, что нам удаётся «разглядеть» идеи детальнее с течением времени. Но вспомним неевклидову геометрию, возникшую только из-за вмешательства в постулат о параллельных прямых, и подумаем о многих других потенциальных геометриях, которые должны существовать в платоновском мире. Все возможные математические идеи и все выводимые из них следствия должны существовать в этом мире на протяжении вечности! Все они должны существовать ещё со времён Большого взрыва!
Вторая основная школа математиков — формалисты. Для них математика — формальная игра, которая начинается с набора строк из абстрактных символов и заключается в выполнении разрешённых преобразований над строками подобно тому, как это происходит в алгебре. Для формалистов математика — чисто механическая игра, где интерпретация символов не разрешена, что не позволяет Вам допустить чисто человеческие ошибки. Основоположник формализма — Давид Гильберт. Этот подход к математике популярен среди людей, работающих в области искусственного интеллекта, потому что такие операции — то, в основном делают машины.
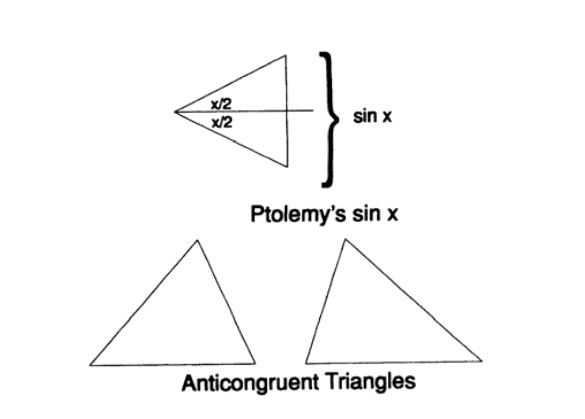
Рис. 1: Возможные отличия в понимании математики
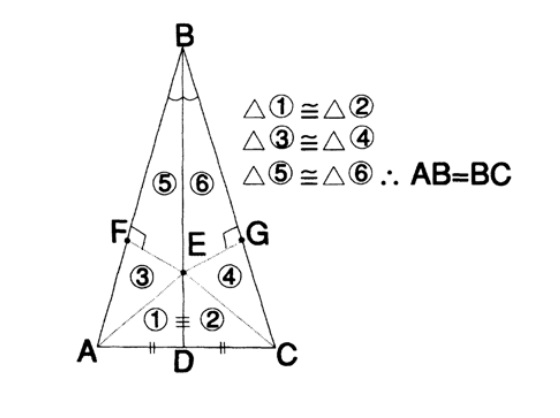
Рис. 2: Доказательство равнобедренности произвольного треугольника
Существует известное с конца Средневековья (хотя я так и не узнал, где это было открыто впервые) общеизвестное доказательство равнобедренности любого треугольника, использующее классическую Евклидову геометрию.
Начнём с треугольника ABC (см. рисунок). Проведём биссектрису из точки B и высоту из точки D (середины AC); эти линии пересекутся в точке E. Из неё опустим перпендикуляры к AB и BC. Верхние два треугольника будут равны по двум углам и общей стороне между ними, нижние два — по равным катетам. Тогда оставшиеся треугольники также будут равны по двум сторонам и углу между ними. Из всего этого следует вывод, что AB=BC, и исходный треугольник является равнобедренным. Очевидно, доказательство теоремы ошибочно, но оно соответствует стилю классических евклидовых геометров, так что здесь изначально присутствует какая-то ошибка. Заметьте, что с помощью метаматематических рассуждений мы пришли к выводу, что математические выкладки привели нас к ошибочному выводу!
Чтобы показать, из-за чего получился ошибочный вывод (и другие возможные ошибки), Гильберт изучил то, что Евклид не описал в своих трудах — понятия расположения между двумя точками (англ. betweenness) и пересечения. С помощью этого Гильберт смог доказать, что показанное пересечение линий происходит вне треугольника, а не внутри него, как показано на чертеже. В процессе этого он ввёл много больше постулатов, чем было описано Евклидом!
Я был аспирантом-математиком, когда это привлекло моё внимание. Я прочитал немного на эту тему и сильно задумался. Насколько мне известно, у Евклида есть около 467 теорем, но ни одна из них не стала ложной после того, как Гильберт добавил свои постулаты. Однако каждая теорема, которая нуждалась в новых постулатах, не могла быть строго доказана по Евклиду! Каждая теорема, которая следовала из таких теорем и опиралась на них, также не была доказана Евклидом. Но результаты в расширенной системе остались теми же, что Евклид ожидал. Как могло получиться, что Евклид, несмотря на то, что он не доказал значительную часть своих теорем, ни разу не ошибся? Удача? Едва ли!
Вскоре мне стало очевидно, что ни одна теорема не была опровергнута из-за того, что Гильберт «знал», что теоремы Евклида были «правильными», и подобрал дополнительные постулаты так, чтобы они согласовывались с теоремами. Но потом я понял, что Евклид был в том же положении: он считал истинной теорему Пифагора, как и многие другие, и должен был найти систему постулатов, которые в итоге дали бы результат, известный ему заранее. Евклид не изложил постулаты и сделал из них выводы, как обычно утверждается; он проложил путь от «известных» результатов к нужным ему постулатам!
Перефразируя одно из утверждений Гильберта, «когда приходит строгость, уходит смысл».
Формалисты утверждают, что в математике нет «смысла» —, но если так, то почему общество должно поддерживать математику и математиков? Почему математика оказалась такой полезной? Если в математике нигде нет смысла, то почему её постулаты и определения меняются со временем? Формалисты попросту не могут объяснить, почему математика является большим, чем праздной игрой наподобие передвижения фигур на шахматной доске.
С формализмом тесно связана школа логицизма, последователи которой попытались свести всю математику в раздел логики. Им, как и многим другим, не удалось выполнить свою задачу — и для них это болезненнее, чем другим, ведь они — логики! Знаменитая попытка Рассела и Уайтхеда, трёхтомник Principia Mathematica, в общем была заброшена, несмотря на то, что значительная часть их работы сохранила свою актуальность. Приведём знаменитую цитату Рассела:
«Чистая математика полностью состоит из предположений, означающих, что если одно утверждение истинно, тогда другое утверждение также истинно в определённом случае. Существенно важно не обсуждать, действительно ли первое утверждение выполняется и что за обстоятельства, в которых истинно второе».
Здесь можно увидеть смесь подходов логицистов и формалистов и чистоту их взглядов. Логицистам не удалось убедить людей, что их подход — не просто упражнение в логике. В самом деле, я утверждаю: то, что считается фундаментом математики, на самом деле — только надстройка. Простой пример, который я привожу годами: если Вы зайдёте ко мне в кабинет и докажете, что теорема Коши ложна, то есть не выполняется из обычных предпосылок, то я определённо буду заинтересован, но в конце концов я попрошу Вас вернуться с новыми предпосылками — я «знаю», что теорема Коши «истинна». Таким образом, по крайней мере, для меня, математика не следует исключительным образом из предпосылок; наборот, очень часто предпосылки следуют из теорем, которые мы полагаем «истинными». Я склонен, как и многие другие, объединять формалистов и логицистов.
Определённо, математика не сводится к формулированию постулатов и строгим дедукциям из них, как это представляют формалисты. Действительно, практически каждый аспирант-математик ощущал, что им приходится подправлять доказательства ранних великих математиков, и каким-то образом теоремы изменяются незначительно, несмотря на то, что их авторы на самом деле не доказывали изменённых теорем. Правда (хоть это и редко упоминается), что определения в математике, как правило, понемногу изменяются со временем, из-за чего предыдущие доказательства больше не могут быть применены к тем же положениям теоремы — её смысл мы теперь понимаем несколько иначе.
Четвёртая школа — интуиционисты, которые однозначно решают дилемму «строгость-смысл», игнорируя строгость. Если Вам нужна абсолютная строгость, то, раз у нас есть всё время повышающийся стандарт строгости, предположительно, ни одна из «доказанных» теорем на самом деле не доказана. Скорее, следующее поколение будет вынуждено подправлять наши результаты, что означает, что мы так ничего и не докажем!
Если хотите знать, я частично интуиционист. Приведённый пример о теореме Коши иллюстрирует мою позицию: математика должна делать то, что я от неё хочу. В отличие от Эрмита (1822–1901), который сказал: «Мы не хозяева, но слуги математики», я склонен считать (время от времени), что мы — хозяева. Постулатов математики не было на скрижалях, которые Моисей принёс с горы Синай; они созданы людьми и поэтому могут меняться как нам заблагорассудится. Ни мой взгляд, ни взгляд Эрмита не являются абсолютно верными, истина где-то посередине: мы и хозяева, и слуги математики.
Природа языка склоняет нас к ответам «да-нет»: что-то есть или чего-то нет, вы либо имеете доказательство, либо нет. Но как только мы признаём, что существует изменяющийся стандарт строгости, мы вынуждены признать, что некоторые доказательства более убедительны, чем другие. Если оценить доказательства по шкале от 0 до 1, как для вероятности, то все они будут внутри этого интервала и, скорее всего, никогда не достигнут верхнего предела в 1 — определённости.
Последняя основная школа — конструктивизм. Его последователи настаивают, что Вы должны предоставить методы построения всего, о чём говорите. Для них неприемлем подход формалистов, которые считают, что, если набор постулатов не признан противоречивым, то определяемые ими объекты «существуют». Конструктивистский подход может доставить много проблем. Ни одна из четырёх других школ не даёт строгого базиса математики, но взгляды конструктивистов слишком строги, так как они исключают слишком много того, что ценно для нас на практике. Специалисты по информатике, за исключением работающих с искусственным интеллектом, обычно считают себя конструктивистами, если вообще об этом задумываются.
В самом деле, некоторые специалисты по численному анализу считают, что система вещественных (real) чисел — это битовые последовательности в компьютере, то есть они по-настоящему реальны. Поэтому утверждается, что «мнимые» числа — действительно мнимые. Но для большинства пользователей математика — просто инструмент, не нуждающийся в осмыслении.
Есть группа людей, работающих с программным обеспечением, которые считают, что мы должны «доказывать корректность программ» так же, как мы доказываем корректность математических теорем. Они совершают две ошибки:
- На самом деле, мы не «доказываем» теоремы!
- Много важных проблем программирования не может быть сформулировано настолько точно, что их можно будет доказать, скорее, возникающая программа определяет проблему!
Это не означает, что в их подходе к доказательству корректности программ нет ничего ценного, только, как это часто бывает, их претензии сильно раздуты. Большинство учёных, занимаясь математикой изо дня в день, относит себя к платоновской школе. Но если заставить их отвечать на вопрос, в чём именно заключается их работа, они обычно находят убежище в формализме, утверждая, что математика — праздная игра с ничего не означающими символами (не то чтобы они в это верили, но это — удобная защитная позиция). Они делают вид, что верят в приведённую цитату Рассела.
Как Вы знаете из своего курса математики, то, что вы действительно делаете, если посмотреть на философском уровне, почти никогда не упоминается. Профессора слишком заняты деталями математики, чтобы обсудить даже то, чем именно они занимаются — типичное поведение технаря!
Однако, как известно, математика в высшей степени полезна в этом мире, и мы используем её, даже не задумываясь об этом. Давайте рассмотрим это подробнее. Древние греки считали, что математика есть истина. В этом практически не было сомнений. Что может быть более истинным, чем 1+1=2? Но вспомните, когда мы обсуждали коды, корректирующие ошибки, мы сказали, что 1+1=0. Эти различные способы использовать одни и те же символы (вы можете утверждать, что единицы в этих двух высказываниях — не одно и то же, если хотите) противоречат логике. Пожалуй, впервые математики столкнулись лицом к лицу с фактом, что могут существовать другие системы математики, когда появились первые неевклидовы геометрии. В них используются те же слова, такие как «точка», «линия», «плоскость», но, очевидно, их значения различны. Это не должно Вас удивлять; когда Вы изучали силы в механике, Вы должны были осознать, что скалярное сложение для векторов неприменимо. А ещё слово «работа» в физике означает не то же самое, что мы обычно имеем в виду
в повседневной жизни.
Математика, которую Вы выбираете для использования, исходит из области применения; она не является универсальной и «истинной». Тогда как мы должны выбирать подходящую математику для различных задач? Какой смысл несут в себе математические символы? Внимательное рассмотрение вопроса подсказывает, что «значение» символа проистекает из того, как он используется, а из определений, как думал Евклид (и Вы), определяя точки, линии и плоскости. Теперь мы понимаем, что его определения двусмысленны и не определяют ничего однозначно; значение исходит из отношений между символами. Это похоже на интерпретируемый язык, набросок которого я привёл в Главе 4: значение инструкции содержится в подпрограмме, которую она вызывает — в том, как символ обрабатывается, а не в его имени! Сами по себе символы — просто битовые строки в машине, и без знания того, как они будут обработаны, смысла в себе не несут.
Математик Доджсон (Льюис Кэрролл), написавший «Алису в Стране Чудес» и «Алису в Зазеркалье», специализировался на логике, и эти две книги — наглядные иллюстрации того, как смысл определяется использованием. Поэтому Шалтай-Болтай говорил: «Когда я беру слово, оно означает то, что я хочу, не больше и не меньше»; Алиса же считала, что слова имеют смысл независимо от их контекста, и их нельзя использовать произвольно.
К этому моменту должно быть понятно, что символы имеют тот смысл, который мы им назначаем. Мы все знакомы с различными естественными языками, где синонимичные слова указывают на один и тот же объект. Возвращаясь к Платону; что есть стул? Это всегда одна и та же идея, или это зависит от контекста? На пикнике булыжник может быть стулом, но Вы не ожидаете, что кто-то использует булыжник как стул в своей спальне. Вы также понимаете, что любой словарь цикличен: первое слово, которое Вы в нём ищете, должно быть определено через другие слова — не может быть начального определения, не использующего слов.
Вследствие этого Вы можете задаться вопросом: как ребёнок изучает язык? Одно дело — выучить второй язык, зная первый, но изучить первый язык — это другое дело, ведь непонятно, где должен возникнуть смысл. Вы можете немного использовать жесты для существительных и глаголов, но многие слова не столь очевидны. Когда я указываю на лошадь и говорю «лошадь», имею ли я в виду имя этой конкретной лошади, всех лошадей, четвероногих, млекопитающих, живых существ? А может, речь идёт о цвете этой лошади? Как другой человек должен узнать, какое значение имеется в виду в конкретной ситуации? В самом деле, как ребёнок учится различать отдельную лошадь и более абстрактный класс лошадей?
По-видимому, как я сказал ранее, смысл возникает при использовании слова, а иначе оно не определено. Несколько лет назад авторы знаменитого словаря признались, что они не способны строго предписать использование слов. Они только могут сказать, как слова используются. Авторам словаря пришлось быть «описательными», не «предписательными». То, что не существует абсолютного, правильного смысла для каждого слова, рассердило многих. Например, и книжный обозреватель New Yorker, и герой детективных романов Ниро Вульф были разгневаны новым словарём. Теперь мы видим, что вся «истина», которая должна быть присуща математике — мираж. Всё это — произвольные, человеческие соглашения.
Но теперь мы сталкиваемся с необоснованно высокой эффективностью математики. Заявив, что в символах математики нет ни «истины», ни «смысла», я затрудняюсь объяснить тот простой факт, что математика используется и является всё увеличивающейся, центральной частью нашего общества, особенно в науке и инженерии.
Мы проделали путь от абсолютной, определённой истины в математике к состоянию, в котором мы не видим смысла в символах —, но мы всё ещё используем их! Мы вкладываем смысл в символы, когда преобразуем задачу в математический вид и когда интерпретируем результаты. Так мы можем использовать одну и ту же формулу во многих различных ситуациях — математика является чем-то вроде универсального умственного инструмента чистого мышления.
Фундаментальный парадокс жизни, описанный Эйнштейном, заключается в том, что мир выглядит логично построенным. Вот самая удивительная вещь — мир может быть познан логически и математически. Я должен предупредить, однако, что последние исследования фундаментальной физики заставляют усомниться в сказанном, и это обсуждается в следующей главе.
Предположим на мгновение, что замечание Эйнштейна верно, тогда задача приложения математики сводится к опознанию сходства между формальной математической структурой и соответствующей частью «реальности». Например, для корректирующих ошибки кодов я должен был выбрать символы кода. Если я должен был использовать 0 и 1 в качестве базовых символов (ошибка была строкой из 0 с одной 1, которая обозначала ошибочную позицию), то я мог «складывать» строки тогда и только тогда, когда я выбирал 1+1=0 как основу своей арифметики: две последовательные ошибки в одной и той же позиции — то же, что отсутствие ошибки. Я должен был увидеть сходство между частями проблемы и математической структурой, которое поначалу я едва понимал.
Таким образом, часть эффективности математики проистекает от выявления аналогии, и только в той степени, в которой аналогия является обширной и точной, мы можем использовать математику для предсказания того, что произойдёт в реальном мире, оперируя символами за письменным столом.
Вы обучены находить многие такие соответствия между математическими моделями и частями реальности. Но я сомневаюсь, что они покроют все будущие разработки. Скорее, так как мы хотим всё больше и больше, включая лучшее понимание самих себя, нам понадобятся многие другие математические модели.
Я предполагаю (совершенно без доказательств) что в прошлом мы нашли простые приложения математики — ситуации с близким соответствием математической структуры и моделируемой сущности. В будущем нам придётся довольствоваться худшими аналогиями между ними. По-моему, со временем нам понадобятся математические модели, в которых целое может быть большим, чем сумма частей, за счёт «синергии» между частями. Вы все знакомы с тем, что организация, в которой Вы находитесь, часто больше, чем множество индивидуалов — есть нравы, средства контроля, привычки, обычаи, история и многое другое, что неотделимо от конкретных людей. Но если математика есть чистое мышление, как я сказал в начале главы, то она должна прийти на помощь для решения подобных проблем в будущем. Иначе говоря, каким бы чистым мышлением Вы ни занимались, особенно если вы используете символы, это математика!
Я хочу завершить на ещё более провокационной ноте. Не является очевидным — хотя многие люди, начиная с древних греков, действуют так, будто это правда — что все вещи, чем бы они ни были, могут быть выражены словами. Вы можете обсуждать всё, что угодно: богов, истину, красоту, справедливость. Но если представить музыкальный концерт, станет ясно, что передаваемое зрителям не может быть выражено словами — если бы это было возможно, композитор и музыканты могли бы ими воспользоваться. В отличие от музыкальной критики, передаваемое музыкой не может быть (по-видимому) вложено в слова. То же, но в меньшей мере, верно для живописи. Поэзия — интересный случай: в ней используются слова, но настоящий смысл заключается не в них!
Аналогично, три столпа Древней Греции, истина, красота и справедливость, не могут быть выражены словами, хотя мы считаем, что они означают. Со времён Хаммурапи (1955–1913 до н.э.) попытка выразить справедливость словами производит закон, и он обычно не совпадает с Вашим пониманием справедливости. В Библии существует знаменитый вопрос «Что есть истина?». И кто, кроме судьи конкурса красоты, посмеет определить «красоту»?
Получается, что мы нарушили ограничения теоремы Гёделя о неполноте, которая, простыми словами, говорит о том, что в достаточно полной системе дискретных символов (теорема не относится к математике, несмотря на то, что обычно её преподносят именно так) найдутся утверждения, чья истинность не может быть доказана в этой системе7? Из неё следует, что при добавлении новых предположений для обоснований подобных утверждений появятся новые, которые не могут быть доказаны в дополненной системе. Это указывает на явный предел возможностей систем дискретных символов.
Язык на первый взгляд является системой дискретных символов. Если же посмотреть пристальнее, теорема Гёделя предполагает набор определённых символов с неизменным значением (хотя оно может зависеть от контекста), но, как мы знаем, слова могут иметь множество значений и степени значений. Например, слово «tall» («длинный»/«высокий»/«долгий») в словосочетаниях «tall building», «tall person», «tall tale» имеет разные значения. Действительно, тон голоса, поднятие брови, подмигивание или даже улыбка могут изменить смысл произносимого слова. Поэтому язык в том виде, в каком мы его на самом деле используем, не подпадает под действие теоремы Гёделя, и, на самом деле, причиной тому, что язык имеет такие необычные свойства, может быть то, что нам требуется обходить ограничения теоремы о неполноте в реальной жизни. Сейчас мы так мало знаем про эволюцию языка и про силы, которые выбрали одну из версий в борьбе за выживание самого приспособленного языка, что можем только гадать, в каких обстоятельствах он развивался.
Стандартные компьютеры могут в настоящее время обрабатывать дискретные символы (хотя с некоторыми нейронными сетями дело обстоит иначе) и, следовательно, существуют вещи, с которыми они не управятся. Как указано в Главе 19, если предположить у нейронных сетей конечную используемую полосу пропускания, то теорема Котельникова даст эквивалентность полосы пропускания и частоты дискретизации.
Я думаю, что в прошлом мы решили простые проблем, и в будущем будем всё больше сталкиваться с оставшимися, которые требуют новых способов мышления и подходов. Проблемы не исчезнут, и Вы будете искать пути их решения. Я предполагаю, что Вам порой придётся изобретать новую математику, чтобы с ними справиться. Будущее будет захватывающим для Вас, если Вы будете решать задачи невероятными, новыми путями.
Очевидно, нас ждёт больше открытий в будущем, чем мы совершили в прошлом!
Продолжение следует…
Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru
- Intro to The Art of Doing Science and Engineering: Learning to Learn (March 28, 1995) (в работе)
- «Foundations of the Digital (Discrete) Revolution» (March 30, 1995) Глава 2. Основы цифровой (дискретной) революции
- «History of Computers — Hardware» (March 31, 1995) (в работе)
- «History of Computers — Software» (April 4, 1995) (в работе)
- «History of Computers — Applications» (April 6, 1995) (в работе)
- «Artificial Intelligence — Part I» (April 7, 1995) (в работе)
- «Artificial Intelligence — Part II» (April 11, 1995) (в работе)
- «Artificial Intelligence III» (April 13, 1995) (в работе)
- «n-Dimensional Space» (April 14, 1995) (в работе)
- «Coding Theory — The Representation of Information, Part I» (April 18, 1995) (в работе)
- «Coding Theory — The Representation of Information, Part II» (April 20, 1995)
- «Error-Correcting Codes» (April 21, 1995) (в работе)
- «Information Theory» (April 25, 1995) (в работе)
- «Digital Filters, Part I» (April 27, 1995)
- «Digital Filters, Part II» (April 28, 1995)
- «Digital Filters, Part III» (May 2, 1995)
- «Digital Filters, Part IV» (May 4, 1995)
- «Simulation, Part I» (May 5, 1995) (в работе)
- «Simulation, Part II» (May 9, 1995)
- «Simulation, Part III» (May 11, 1995)
- «Fiber Optics» (May 12, 1995)
- «Computer Aided Instruction» (May 16, 1995) (в работе)
- «Mathematics» (May 18, 1995) (в работе)
- «Quantum Mechanics» (May 19, 1995) Глава 24. Квантовая механика
- «Creativity» (May 23, 1995). Перевод: Глава 25. Креативность
- «Experts» (May 25, 1995) (в работе)
- «Unreliable Data» (May 26, 1995)
- «Systems Engineering» (May 30, 1995) Глава 28. Системная Инженерия
- «You Get What You Measure» (June 1, 1995) (в работе)
- «How Do We Know What We Know» (June 2, 1995)
- Hamming, «You and Your Research» (June 6, 1995). Перевод: Вы и ваша работа
Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru
