[Перевод] Реализация псевдо-3D в гоночных играх

Введение
Почему псевдо-3d?
Зачем кому-то захочется создавать дороги в олдскульном стиле сегодня, когда каждый компьютер может на лету отрисовывать графику, состоящую из миллионов полигонов? Разве полигоны — не то же самое, только лучше? На самом деле нет. Полигоны действительно создают меньше искажений, но именно деформации в старых игровых движках дают такое сюрреалистичное, головокружительное чувство скорости, ощущаемое во многих дополигональных играх. Представьте, что область видимости управляется камерой. При движении по кривой в игре, использующей один из таких движков, похоже, что она заглядывает на кривую. Затем, когда дорога становится прямой, вид тоже выпрямляется. При движении в повороте с плохим обзором камера как будто заглядывает за выступ. И поскольку в таких играх не используется традиционный формат трасс с точными пространственными соотношениями, то можно без проблем создавать трассы, на которых игрок будет ездить с захватывающей дух скоростью. При этом не нужно беспокоиться о том, что объекты появляются на трассе быстрее, чем может среагировать игрок, потому что физическую реальность игры можно легко изменять в соответствии со стилем геймплея.
Но в такой системе есть и множество недостатков. Глубина физики, используемой в играх-симуляторах, будет утеряна, поэтому такие движки не приспособлены для этих игр. Однако они просты в реализации, быстро работают, а игры на их основе обычно очень интересны!
Стоит заметить, что не в каждой старой гоночной игре используются эти техники. В действительности описываемый в статье метод — это только один из способов создания псевдотрёхмерной дороги. В других случаях используются спроецированные и отмасштабированные спрайты или различные способы реального проецирования дороги. Степень смешения реальной математики с трюками зависит от создателей. Надеюсь, вам понравится изучение предложенного мной спецэффекта.
Насколько хорошо нужно разбираться в математике?
Если вы…
… знаете тригонометрию, то её будет вполне достаточно для понимания всего туториала
… знаете только алгебру и геометрию, то пропустите объяснение «области видимости»
… хотите избежать математических объяснений, то читайте разделы «Простейшая дорога», «Кривые и повороты», «Спрайты и данные» и «Холмы».
Это универсальная техника, и разбираться подробнее можно, просто добавляя соответствующие разделы. Если вы знаете сложную математику, то вам будет интересно, но если вы разбираетесь только в арифметике, до сможете достичь уровня детализации, созданного в таких играх, как Pole Position или в первой OutRun.
Насколько хорошо нужно знать программирование?
Если вы понимаете растровую графику, то это сильно поможет: достаточно знать, что такое строка развёртки (scanline), и что каждая строка состоит из ряда пикселей. Примеры программ написаны на псевдокоде, поэтому знание какого-то конкретного языка не требуется.
Готовы? Приступим!
Растровые эффекты: небольшое предисловие
Псевдотрёхмерная дорога — это один из случаев более общего класса эффектов, называемых растровыми эффектами. Наиболее известные из растровых эффектов используются в Street Fighter II: при перемещении бойцов влево или вправо поверхность земли изменяется в перспективе. Но это на самом деле не 3D. Графика поверхности хранится как очень широкоугольный снимок. При скроллинге строки экрана, которые находятся «дальше», перемещаются медленнее, чем более близкие. То есть каждая строка на экране перемещается независимо от другой. Ниже показан конечный результат и то, как графика поверхности земли хранится в памяти


Основы создания дорог
Введение в растровые дороги
Мы привыкли воспринимать 3D-эффекты в рамках полигонов, чьи вершины подвешены в трёхмерном пространстве. Однако старые компьютеры были недостаточно мощными, чтобы справляться с большим количеством трёхмерных вычислений. Поэтому чаще всего в старых играх использовались растровые эффекты. Это особые эффекты, создаваемые построчным изменением переменной. Это хорошо подходит для работы старого графического оборудования, имевшего аппаратное ускорение скроллинга и использовавшего режим индексированных цветов.
Растровый эффект псевдодороги на самом деле создавался почти так же, как эффект перспективы в Street Fighter II, где статичное изображение деформировалось для добавления иллюзии трёхмерности. Вот как это реализовывалось:
Большинство растровых дорог начинается с изображения плоской дороги. В сущности, это графическое изображение двух параллельных линий на земле, уходящих вдаль. При отдалении эти линии кажутся наблюдателю соединяющимися. Это основное правило перспективы. Кроме того, чтобы создать иллюзию движения, у большинства аркадных гоночных игр на дороге рисовались полосы. Перемещение этих полос на дороге достигалось или цикличным переключением цветов или изменением палитры каждой строки. Кривые и повороты выполнялись независимым скроллингом каждой строки, как в Street Fighter II.
Мы рассмотрим кривые и повороты в следующем разделе. А пока давайте сконцентрируемся на скроллинге дороги вперёд.
Простейшая дорога
Возьмём изображение дороги, описанной выше: две параллельные линии, обозначающие правую и левую сторону дороги, уходящие вдаль. Удаляясь от наблюдателя, они становятся всё ближе. Вот пример того, как это может выглядеть:

В этом изображении не хватает дорожной разметки, создающей хорошее ощущение перспективы. Для этого эффекта в играх, кроме прочей дорожной разметки, используются попеременные тёмные и светлые полосы. Чтобы добавить их, давайте определим переменную «положения текстуры». Эта переменная равна нулю внизу экрана и с каждой линией вверх увеличивает своё значение. Когда её значение ниже определённого числа, дорога рисуется одним оттенком. Когда значение выше этого числа, она рисуется другим оттенком. После превышения максимального значения переменная положения снова приравнивается к нулю, создавая повторяющийся шаблон.
Однако менять его для каждой строки недостаточно, потому что тогда получится всего лишь несколько полос разных цветов, которые не уменьшаются с удалением дороги. Значит, нужна другая переменная, которая будет изменяться на заданную величину. Её нужно прибавлять к другой переменной каждую строку, а потом прибавлять последнюю к изменению положения текстуры.
Вот пример того, как меняется значение Z для каждой строки при движении вдаль. После переменных я написал то, что нужно прибавить, чтобы получить значения для следующей строки. Я назвал значения DDZ (дельта-дельта-Z), DZ (дельта-Z) и Z. DDZ остаётся постоянной, DZ меняется линейно, а Z — по кривой. Можно считать Z координатой положения Z, DZ — скоростью положения, а DDZ — ускорением положения (изменением ускорения). Учтите, что значение »4» выбрано произвольно, потому что удобно для этого примера.
DDZ = 4 DZ = 0 Z = 0 : dz += 4, z += 4
DDZ = 4 DZ = 4 Z = 4 : dz += 4, z += 8
DDZ = 4 DZ = 8 Z = 12 : dz += 4, z += 12
DDZ = 4 DZ = 12 Z = 24 : dz += 4, z += 16
DDZ = 4 DZ = 16 Z = 40 : и т.д.
Заметьте, что DZ изменяется первой, а потом используется для изменения Z. Это можно объяснить так: допустим, мы движемся по текстуре со скоростью 4. Это значит, что после первой строки мы считываем текстуру в положении 4. Следующая строка будет в положении 12. После неё 24. Таким образом, проход по текстуре происходит всё быстрее и быстрее. Поэтому я и называю эти переменные «положением текстуры» (место текстуры, которое мы считываем), «скоростью текстуры» (как быстро мы проходим через текстуру) и «ускорением текстуры» (насколько быстро меняется скорость текстуры).
Похожий способ мы используем для отрисовки кривых и холмов без слишком большого количества расчётов. Теперь, чтобы создать иллюзию движения текстуры нужно просто менять для каждого кадра начало положения текстуры в нижней части экрана.
Можно заметить недостаток этого трюка: коэффициент масштабирования неточен. Это приводит к искажению, которое я буду называть «эффектом овсянки». Такой эффект деформации присутствовал в ранних псевдотрёхмерных играх, например в OutRun: объекты, в том числе полосы на дороге, казалось, замедлялись при движении от центра экрана наружу.
Этот способ нахождения значения Z имеет ещё один недостаток: непросто предсказать, каким будет значение на каждом расстоянии, особенно при использовании холмов. Мы узнаем более сложный способ, который я называю Z-картой (Z-map). Это таблица, вычисляющая расстояние Z для каждой растровой строки экрана. Но сначала нам нужно ещё немного математики…
Экскурс в математику: проекция трёхмерной перспективы
Существуют способы избавления от эффекта овсянки. Однако для их реализации нужны знания традиционной трёхмерной математики. Нам нужно найти способ трансляции 3D-координат, чтобы их можно было расположить на 2D-поверхности.
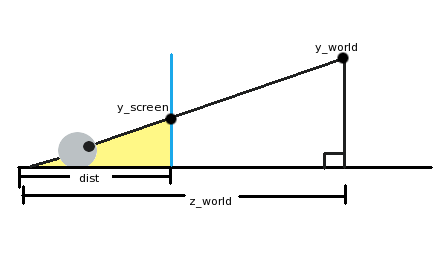
На рисунке выше глаз (в левом нижнем углу) смотрит сквозь экран (синяя вертикальная линия) на объект в нашем трёхмерном мире («y_world»). Глаз находится на расстоянии «dist» от экрана, и на расстоянии «z_world» от объекта. Если вы занимались геометрией или тригонометрией, то могли заметить, что на картинке есть не один, а два треугольника. Первый треугольник — большой, от глаза до поверхности справа и вверх до объекта, на который смотрит глаз. Второй треугольник я закрасил жёлтым. Он образуется глазом, точкой на экране, в которой мы видим объект, и поверхностью.
Гипотенузы этих двух треугольников (линии от глаза до объекта) находятся под одним углом, хотя одна и длиннее другой. В сущности, это один и тот же треугольник, только уменьшенный в масштабе. Это означает, что соотношение горизонтальных и вертикальных сторон будет одинаковым! В математической записи:
y_screen/dist = y_world/z_world
Теперь нам нужно преобразовать уравнение, чтобы получить y_screen. Получаем:
y_screen = (y_world*dist)/z_world
То есть для нахождения координаты y объекта на экране мы берём координату y мира, умножаем её на расстояние от глаза до экрана, а затем делим на расстояние в мире. Разумеется, если мы так поступим, то центр взгляда будет в левом верхнем углу экрана! Чтобы убедиться в этом, достаточно подставить y_world=0. Для центрирования нужно прибавить к результату половину разрешения экрана. Уравнение можно немного упростить, если представить, что нос прижат к экрану. В этом случае dist=1. Получается следующее уравнение:
y_screen = (y_world/z_world) + (y_resolution/2)
Есть связь между соотношениями и углом обзора, а также масштабированием изображения, чтобы оно не зависело от разрешения экрана. Но для решения проблемы с дорогой нам это не понадобится. Если вам интересно, посмотрите на схему в виде сверху: угол до края экрана — это область видимости, и та же связь сохраняется.
Ещё математика: добавление области видимости к трёхмерной проекции
Вообще-то это обычно не нужно для большинства «дорожных» движков. Но это полезно для того, чтобы параметры проецирования не зависели от разрешения, или для объектов, которые нужно вращать, или для интеграции с подлинными 3D-эффектами.
Давайте вернёмся к исходной формуле проецирования. Величина «dist» из уравнений выше здесь будет называться «scaling»:
y_screen = (y_world*scaling)/z_world + (y_resolution/2)
Идея заключатся в том, что нам нужно отмасштабировать все точки на экране на определённую величину, что позволит оставаться видимыми точкам в пределах области видимости (field-of-view, FOV). Для оси x FOV и оси y FOV нужны будут две константы.
Например, предположим, что мы работаем в разрешении 640×480 и хотим, чтобы FOV была равна 60 градусам. Мы видели схему трёхмерной проекции в виде сбоку. Для этого случая давайте посмотрим на схему проецируемого пространства в виде сверху:
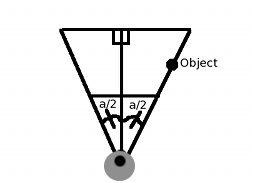
Один из способов решения проблемы — принять, что если объект находится с правой стороны нашей FOV, он должен отображаться на экране в положении x=640 (потому что разрешение экрана 640×480). Если посмотреть на схему, то можно заметить, что FOV можно разделить на два прямоугольных треугольника, в которых угол каждого равен fov_angle/2 (a/2). И поскольку наша FOV является конусом, то объект, находящийся на правом крае FOV, т.е. x=R*sin (a/2) и
z=R*cos (a/2), где R — любое значение радиуса. Мы можем, например, взять R=1. И нам нужно, чтобы объект отображался на экране в x_screen=640. Получаем следующее (с учётом основной формулы проецирования):
x_screen=640 fov_angle=60 y_world=sin(60/2) z_world=(60/2) x_resolution/2=320 scaling=?
x_screen = (y_world*scaling)/z_world + (x_resolution/2)
640 = (sin (30)*scaling/cos (30)) + 320
320 = tan (30)*scaling
320/tan (30) = scaling
В общем случае: scaling = (x_resolution/2) / tan (fov_angle/2)
Мы заменили a/2 на 30 (половина от 60 градусов), обозначили sin/cos = tan, и вуаля! Можно проверить это, поместив объект в правый конец области видимости, подставив эти значения в исходное уравнение проецирования и убедившись, что X принимает значение 640. Например, точка (x, z) с координатами (20, 34.64) окажется в X=640, потому что 20 — это 40*sin (30), а 34.64 — это 40*cos (30).
Нужно заметить, что значения FOV для горизонтальной (x) и вертикальной (y) осей будут разными у стандартного и широкоэкранного монитора в горизонтальном положении.
Более точная дорога: использование Z-карты
Для решения проблемы с перспективной нам нужно создать предварительно вычисленный список расстояний для каждой строки экрана. Если вкратце, то проблема заключается в описании плоскости в 3D.
Чтобы понять, как это работает, представьте сначала двухмерный аналог: линию! Для описания горизонтальной линии в 2D, можно сказать, что для каждой пары координат (x, y) координата y будет одной и той же.
Если мы выведем её в трёхмерное пространство, то линия станет плоскостью: для каждого расстояния x и z координата y будет оставаться той же! Если рассматривать плоскую горизонтальную поверхность, то не важно, насколько далеко расположена камера, y будет постоянной. Также не важно, насколько далеко влево или вправо расположена точка, значение y всегда будет таким же.
Вернёмся к выяснению расстояния до каждой из строк экрана: назовём наш список Z-картой. Вопрос вычисления Z-карты заключается в преобразовании формулы трёхмерного проецирования для нахождения значения Z для каждого экранного Y!
Сначала возьмём уравнение из предыдущего раздела:
Y_screen = (Y_world / Z) + (y_resolution / 2)
Поскольку у нас есть Y_screen (каждая строка), преобразуем уравнение, чтобы найти Z:
Z = Y_world / (Y_screen - (height_screen / 2))
Y_world в целом является разностью между уровнем земли и высотой камеры, которая будет отрицательной. Она одинакова для каждой строки, потому что, как сказано во вводном параграфе, нас пока интересует плоская дорога. Кроме того, что дорога будет выглядеть более чётко и избежит «эффекта овсянки», есть ещё одно преимущество: простота расчёта максимального расстояния отрисовки.
Дорога располагается на экране считыванием этого буфера: для каждого расстояния необходимо выяснить, какая часть текстуры дороги принадлежит ему, заметив, сколько единиц занимает каждая строка или пиксель текстуры.
Хотя мы знаем расстояние для каждого ряда экрана, может оказаться полезным кэшировать для каждой строки или ширину дороги, или коэффициент масштабирования. Коэффициент масштабирования противоположен расстоянию, выбранному таким образом, что значение на строке, в которой графическое изображение машины игрока находится больше всего, равнялось 1. Его можно использовать для масштабирования спрайтов на заданной строке или для определения ширины дороги.
Кривые и повороты
Создаём изгибы
Чтобы сделать дорогу кривой, надо просто изменить положение центральной линии по форме кривой. Для этого можно использовать пару способов. Один способ — это такой же способ, которым создавались положения Z в разделе «Простейшая дорога»: с помощью трёх переменных. То есть начиная с низа экрана величина, на которую смещается центр дороги влево или вправо каждую строку, стабильно увеличивается. Как и в случае со считыванием текстуры, мы можем считать эти переменные положением центральной линии (кривой), скоростью кривой и ускорением кривой.
Однако у этого способа есть проблемы. Одна из них в том, что не очень удобно создание S-образных кривых. Ещё одно ограничение: вход в поворот выглядит точно так же, как и выход их него: дорога загибается, а потом просто разгибается.
Чтобы улучшить ситуацию, можно ввести понятие сегментов дороги. Сегмент дороги — это часть, невидимая игроку. Можно считать его невидимым горизонтальным разделителем, устанавливающим кривизну дороги над этой строкой. В любой момент времени один из этих сегментных разделителей находится внизу экрана, а другой проходит вниз с постоянным темпом до самого низа. Давайте назовём нижний сегмент базовым, потому что он задаёт начальную кривизну дороги. Вот как это работает:
Когда мы начинаем отрисовывать дорогу, то начинаем с того, что смотрим на базовую точку и соответственно устанавливаем параметры отрисовки. С приближением поворота его строка сегмента находится на расстоянии и приближается к игроку почти как любой другой дорожный объект, за исключением того, что она должна спускаться вниз по экрану с постоянным темпом. То есть при конкретной скорости, с которой движется игрок, сегментный разделитель опускается вниз по экрану на такое же количество линий за кадр. Или, если используется Z-карта, на то же количество элементов z-карты за кадр. Если бы сегмент «ускорялся» по направлению к игроку, как делают 3d-объекты на трассе, то дорога бы изгибалась слишком резко.
Давайте посмотрим, как это работает. Предположим, что строка сегмента для левой кривой находится спустилась вниз на полдороги, а базовый сегмент является просто прямой дорогой. При отрисовке дороги она не будет начинать изгибаться, пока не столкнётся с сегментом «левой кривой». Потом кривая дороги начинает изменяться с темпом, указанным этой точкой. Когда движущийся сегмент достигает низа экрана, он становится новым базовым сегментом, а предыдущий базовый сегмент поднимается наверх дороги.
Ниже показаны две дороги: одна прямая, за которой идёт левый поворот, а другая с изгибом влево, за которым идёт прямая. В обоих этих случаях положение сегмента находится на полпути вниз по Z-карте (или на полпути вниз по экрану). Другими словами, дорога начинает изгибаться или становиться прямой на полпути вниз по дороге. На первом рисунке камера входит в поворот, а на втором — выходит из него.


А вот та же техника и то же положение сегмента, применённые к S-образной кривой:

Наилучший способ отслеживания положения сегмента — определять, где он находится на Z-карте. То есть не привязывать положение сегмента к положению Y на экране, а привязать его к положению на Z-карте. Таким образом он всё равно будет начинаться на горизонте дороги, но работать с холмами станет гораздо удобнее. Следует учесть, что на плоской дороге без смен высот эти два способа отслеживания положения сегмента аналогичны.
Давайте проиллюстрируем вышесказанное кодом:
current_x = 160 // половина экрана шириной 320
dx = 0 // величина кривой, постоянная для сегмента
ddx = 0 // величина кривой, изменяется построчно
для каждой строки экрана, снизу вверх:
если строка положения экранной Z-карты ниже segment.position:
dx = bottom_segment.dx
иначе если строка положения экранной Z -карты выше segment.position:
dx = segment.dx
конец "если"
ddx += dx
current_x += ddx
this_line.x = current_x
конец "для"
// Перемещение сегментов
segment_y += constant * speed // Константа гарантирует, что сегмент не будет двигаться слишком быстро
если segment.position < 0 // 0 - ближайшее
bottom_segment = segment
segment.position = zmap.length — 1 // Отправить положение сегмента на самое дальнее расстояние
segment.dx = GetNextDxFromTrack () // Получить новую величину кривой из данных трассы
конец «если»
Одно из больших преимуществ реализации кривых таким способом заключается в том, что если есть кривая, за которой следует прямая дорога, то игрок сможет увидеть прямую дорогу при выходе из кривой. Аналогично, если за кривой следует кривая в другом направлении (или даже более изогнутая кривая в том же направлении), то игрок может увидеть этот следующий участок трассы до того, как попадёт на него.
Чтобы иллюзия была полной, нужно добавить графику горизонта. С приближением кривой горизонт не меняется (или перемещается незначительно). Затем, когда кривая полностью отрисована, принимается, что машина поворачивает по ней, а горизонт быстро прокручивается в направлении, противоположном направлению кривой. Когда кривая снова выпрямляется, фон продолжает прокручиваться, пока кривая не закончится. Если вы используете сегменты, то можно просто выполнять прокрутку (скроллинг) горизонта в соответствии с настройками базового сегмента.
Общая формула кривых
Изучив технику кривых, подробно описанную в разделе «Простейшая дорога», мы можем сделать интересный вывод. Этот вывод больше относится к математике, чем к изложенному выше материалу, и его можно спокойно пропустить, если ваш графический движок не должен быть независимым от разрешения или использует технику »3d-спроецированных сегментов», рассмотренную в разделе о холмах.
Рассматривая пример кривой, использующей «Z», из раздела «Простейшая дорога», можно заметить, что z-положение (или x-положение) заданной строки является суммой возрастающего ряда чисел (например, 1 + 2 + 3 + 4). Такой ряд называется арифметическим рядом или арифметической прогрессией. Если использовать вместо 1 + 2 + 3 + 4, например 2 + 4 + 6 + 8 или 2×1 + 2×2 + 2×3 + 2×4, можно получить более резкую кривую.»2» в этом случае — переменная segment.dx. Её можно также факторизировать, получив 2(1 + 2 + 3 + 4)! Теперь всё, что нужно сделать — найти формулу, описывающую 1 + 2 +… + N, где N — количество строк, составляющих кривую. Известно, что сумма арифметической прогрессии равна N (N+1)/2. Поэтому формулу можно записать как s = A * [ N (N+1)/2 ], где A — резкость кривой, а s — сумма. Это уравнение можно ещё преобразовать для добавления стартовой точки, например, центра дороги снизу экрана. Если мы обозначим её за «x», то получим s = x + A * [ N (N+1)/2 ].
Теперь у нас есть формула для описания кривой. Мы хотим получить ответ на вопрос «зная стартовую точку x и N строк кривой, каким должно быть A, чтобы кривая достигла в конце x-положения, равного s?» Преобразовав уравнение для нахождения A, мы получим A = 2(s — x)/[n (n+1)]. Это значит, что резкость заданной кривой может храниться относительно положения X, что делает графический движок независимым от разрешения.
Повороты в перспективном стиле
Гораздо менее интересно, когда при поворотах в игре двигается только спрайт машины. Поэтому вместо перемещения спрайта автомобиля игрока мы оставим его в центре экрана и будем двигать дорогу, и что более важно, двигать положение центральной линии в передней (т.е. нижней) части экрана. Теперь примем, что игрок будет всегда смотреть на дорогу, поэтому сделаем так, чтобы дорога заканчивалась в центре экрана. Для этого будет нужна переменная угла дороги. Поэтому вычислим разницу между центром экрана и положением передней части дороги, а затем разделим на высотe графики дороги. Это даст нам величину для перемещения центра дороги на каждой строке.
Спрайты и данные
Расположение объектов и масштабирование
Спрайты нужно отрисовывать сзади вперёд. Иногда такой способ называют алгоритмом художника. Для этого нужно заранее определить, где на экране должен отрисовываться каждый объект, а затем отрисовать объекты на разных этапах.
Выполняется это следующим способом: когда мы проходим по Z-карте при отрисовке дороги, нужно также отмечать, с какой строкой экрана должен быть связан каждый спрайт. Если спрайты сортировались по Z, это тривиально: каждый раз при считывании нового значения Z-карты нужно проверять, находится ли положение Z следующего спрайта ближе к камере, чем текущее значение Z-карты, или равны ли они. Если это так, то надо пометить экранное положение Y спрайта как принадлежащее к текущей строке. Затем проверить следующий спрайт тем же способом. Продолжать этот процесс, пока не получим из списка спрайт, положение которого по Z дальше, чем текущее.
Положение X объекта необходимо отслеживать относительно центра дороги. Тогда простейшим способом горизонтального позиционирования спрайта является умножение значения на коэффициент масштаба текущей строки (величину, обратную Z) и прибавление результата к центру дороги.
Хранение данных трассы
Когда я делал моё первое демо с дорогой, я хранил информацию уровня в списке событий, которые должны произойти на определённых расстояниях. Разумеется, расстояния указывались в единицах положения текстуры. События состояли из команд начала и завершения кривых. Насколько я помню, скорость, с которой дорога начинает и заканчивает изгибаться, произвольна. Единственное правило — она должна соответствовать скорости машины игрока.
Однако если вы используете систему с сегментацией, то можно просто использовать список команд. Расстояние, которое занимает каждая команда, аналогична скорости перемещения невидимого сегмента к низу экрана. Это также позволяет создать формат трассы, работающий для тайловой карты, позволяющей передать довольно реалистичную географию трассы. То есть каждый тайл может быть одним сегментом. Резкий поворот может повернуть трассу на 90 градусов, а более плавный — на 45 градусов.
Текстурирование дороги
Теперь вам возможно захочется использовать на дороге настоящую графическую текстуру вместо меняющихся линий, которые у нас созданы на данный момент. Для этого можно использовать пару способов. Дешёвый и простой способ: подготовить пару текстур для дороги (для эффекта сменяющихся линий). При отрисовке каждой горизонтальной строки дороги нужно растянуть текстуру, чтобы она соответствовала ширине этой строки. Или, если растягивание невозможно, нужно выбрать строку одного из двух полных битовых изображений дороги (подход, использованный в Outrunners).
Если хотите, чтобы дорога выглядела более точной, сделайте так, чтобы Z для каждой строки соответствовала номеру строки графической текстуры. И вуаля! Единая затекстуренная дорога!
Однако если вам нужны только полосы сменяющихся цветов, ответ ещё более прост, особенно при использовании фиксированной точки. Для каждой Z нужно сделать так, чтобы один из битов представлял оттенок дороги (тёмный или светлый). Затем просто отрисовывайте соответствующий рисунок дороги из цветов для этого бита.
Холмы
Вариации холмов
Похоже, что существует почти бесконечное количество способов создания эффектов холмов. Эффекты холмов могут создаваться с широким диапазоном геометрической точности, причём некоторые менее точные техники создают более убедительные результаты. Мы рассмотрим два возможных способа.
Фальшивые холмы
После множества экспериментов я пришёл к гибкому способу имитации холмов, который использует мало расчётов. Кроме того, он точно отслеживает объекты, находящиеся ниже горизонта. Это эффект масштабирования и деформации, вертикально растягивающий и сжимающий дорогу. Для генерирования кривизны холма в нём используется тот же трюк с суммированием, который применялся для отрисовки кривых.
Вот как это делается: во-первых, цикл отрисовки должен начинаться с начала Z-карты (ближайшего) и останавливаться, когда доберётся до конца (самого дальнего). Если мы будем уменьшать положение отрисовки каждой строки на 1, то дорога будет отрисована плоской. Однако если уменьшать положение отрисовки каждой строки на 2, удваивая строки в проходе, то дорога будет отрисовываться в два раза выше. И, наконец, варьируя величину декремента положения отрисовки каждой линии можно отрисовать холм, начинающийся как плоскость и поднимающийся вверх. Если следующее положение отрисовки находится дальше от текущего положения отрисовки больше, чем на одну строку, то текущая строка Z-карты повторяется, пока мы не доберёмся до неё, создавая эффект масштабирования.
Спуски с холмов делаются похожим образом: если положение отрисовки увеличивается, а не уменьшается, то мы опустимся ниже последней отрисованной строки. Разумеется, строки, находящиеся ниже горизонта, не будут видимы на экране. Отрисовываются только линии, находящиеся на один или больше пикселей выше последней строки. Однако нам всё равно нужно отслеживать объекты, находящиеся ниже горизонта. Для этого нужно учесть положение Y каждого спрайта при обходе Z-карты. Может помочь создание Z-карты, большей, чем необходимо для плоской дороги. Таким образом при растяжении буфера она не станет слишком пикселизированной.
Теперь нам нужно сдвинуть горизонт, чтобы для игрока картинка была убедительной. Я люблю использовать фон в стиле игры «Lotus»: в ней горизонт не просто состоит из очертаний неба, но и из графики отдалённой земли. Когда холм поднимается вверх (увеличивая область видимости), горизонт должен немного опуститься вниз относительно верхней части дороги. Когда холм спускается вниз и камера «упирается» в холм (ограничивая область видимости), горизонт должен подниматься вверх.
Вот как выглядит эффект для спуска с холма и подъёма на него, разумеется, без графики горизонта:


Плюсы
- Малая нагрузка при расчётах: не требуется умножение или деление
- Отслеживаются объекты на обратной стороне холма
- Кажется, что угол обзора следует за игроком проезде по холмам
Минусы
- Точная 3d-геометрия невозможна
- Для создания убедительного эффекта требуется тонкая настройка
Подведение итогов: дальнейшее развитие растровых дорог
Такие формулы кривых с накоплением можно гибко использовать, если вам не требуются безумные кривые или огромные холмы. Во многих играх, использующих такие трюки, дорога скроллится так быстро, что даже небольшая кривая выглядит убедительно.
Однако, для создания более впечатляющей дороги вам может понадобиться преувеличить эффект. В любой из этих формул кривых можно использовать высокие значения ddx или ddy, но dx или dy не должны превышать разумных значений. Пользователь YouTube Foppygames обнаружил ещё один трюк, создающий более крутые кривые из этих формул с накоплением: нужно для каждой строки умножать значение dx или dy на значение z! Это делает кривую более крутой на расстоянии, чем она есть на переднем плане, и создаёт довольно убедительный эффект.
И эксперименты на этом не заканчиваются. На самом деле, самое хорошее в таких движках — это то, что нет «правильных» способов их реализации. Всё, что создаёт приятные глазу кривые и изгибы, всячески приветствуется! В моём первом дорожном движке я использовал для изгибов дороги синусоидную таблицу поиска.
Можно также использовать умножение: для смещения дороги вправо можно, например, умножать положение x на 1,01 для каждой строки. Для смещения влево на ту же величину нужно умножить на 0,99 или 1/1,01 (величину, обратную 1,01). Однако, вооружившись знаниями о том, что многие старые процессоры не имели операций умножения или были слабы в нём, я остановился на технике накопления, потому что в ней используется только сложение. Она показалась мне более «аутентичным» способом создания изгибов дороги.
В некоторых играх, например, в OutRun, даже используется система простых сплайнов (по крайней мере, если судить по сделанному на основе реверс-инжиниринга отличному порту на C++ Cannonball.
Вот так, играя и экспериментируя, вы сможете выбрать самую подходящую вам технику!
… или продолжить чтение, чтобы узнать хитрый трюк, смешивающий 3d-полигоны. Он почти так же быстр, даже более убедителен и может воспроизводиться на том же старом растровом оборудовании. Заинтригованы?
Настоящие 3d-спроецированные сегменты
Сравнение 3d-спроецированных сегментов и растровых дорог
Растровые дороги красивы, но их можно сделать ещё более впечатляющими благодаря использованию простого способа рендеринга полигонов. Этот способ рендеринга может «потянуть» даже такое же слабое растровое оборудование. Однако в нём используется больше вычислений.
Известно, что этот трюк использовался в таких играх как Road Rash и Test Drive II: The Duel. Вот в чём он заключается: трасса состоит из полигональных сегментов. Однако вместо перемещения в полном 3d-пространстве, они двигаются только относительно камеры. Для кривых дорога по-прежнему наклоняется влево или вправо, почти так же, как в растровых дорогах: здесь нет действительного вращения, которое бы присутствовало при поворотах на кривой в полностью полигональном движке.
Вот краткое объяснение принципа:
- Поскольку кривые и углы дорог по-прежнему имитируются, затратные вычисления вращения не будут нужны
- В сущности, дорога является полосой из четырёхугольников: каждая секция дороги соединена со следующей секцией. Это значит, что мы можем вычислить, видимость части дороги только на основании её экранного положения Y относительно предыдущего соседа.
- Отношения между этими четырёхугольниками никогда не меняются. То есть угол на самом деле никогда не меняется, поэтому четырёхугольники всегда и автоматически сортируются по Z.
Простая 3d-дорога
Во-первых, разобь
