[Перевод] Раскрыта тайная связь чистой математики и физики
Выдающийся математик раскрыл подробности того, как его успехи в изучении тысячелетних математических вопросах связаны с концепциями, взятыми из физики

Миньон Ким
В математике полно странных числовых систем, о которых большинство людей никогда не слышало. Некоторые из них даже сложно будет представить. Но рациональные числа знакомы всем. Это числа для счёта предметов и дроби — все числа, известные нам с начальной школы. Но в математике иногда сложнее всего понять самые простые вещи. Они простые, как гладкая стена, без трещин и выступов, или других очевидных свойств, за которые можно было бы ухватиться.
Миньон Ким, [Minhyong Kim] математик из Оксфордского университета, особенно интересуется вопросом того, какие рациональные числа подходят для решения уравнений определённого рода. Эта проблема стимулировала специалистов по теории чисел тысячелетиями. И они едва продвинулись по пути к её решению. Когда вопрос изучается так долго и без ответа, можно заключить, что единственным способом продвинуться в нём будет выдвинуть радикально новую идею. Именно это и проделал Ким.
«Техник существует не так много, хотя мы и работаем над этим последние 3000 лет. Так что когда кто-нибудь предъявляет по-настоящему новый способ это делать, это представляет большой интерес —, а Миньон сделал именно это», — говорит Джордан Элленберг [Jordan Ellenberg], математик из Висконсинского университета в Мэдисоне.
За последнее десятилетие Ким описал совершенно новый способ поиска закономерностей в кажущемся беспорядочном мире рациональных чисел. Он описал этот метод в статьях и на конференциях, и передал его студентам, ныне продолжающим эту работу самостоятельно. Но он всегда что-то приберегал. Его видение, дававшее жизнь его идеям, было основано не на чистом мире чисел, а на концепциях, позаимствованных у физики. Для Кима рациональные решения чем-то напоминают траекторию света.
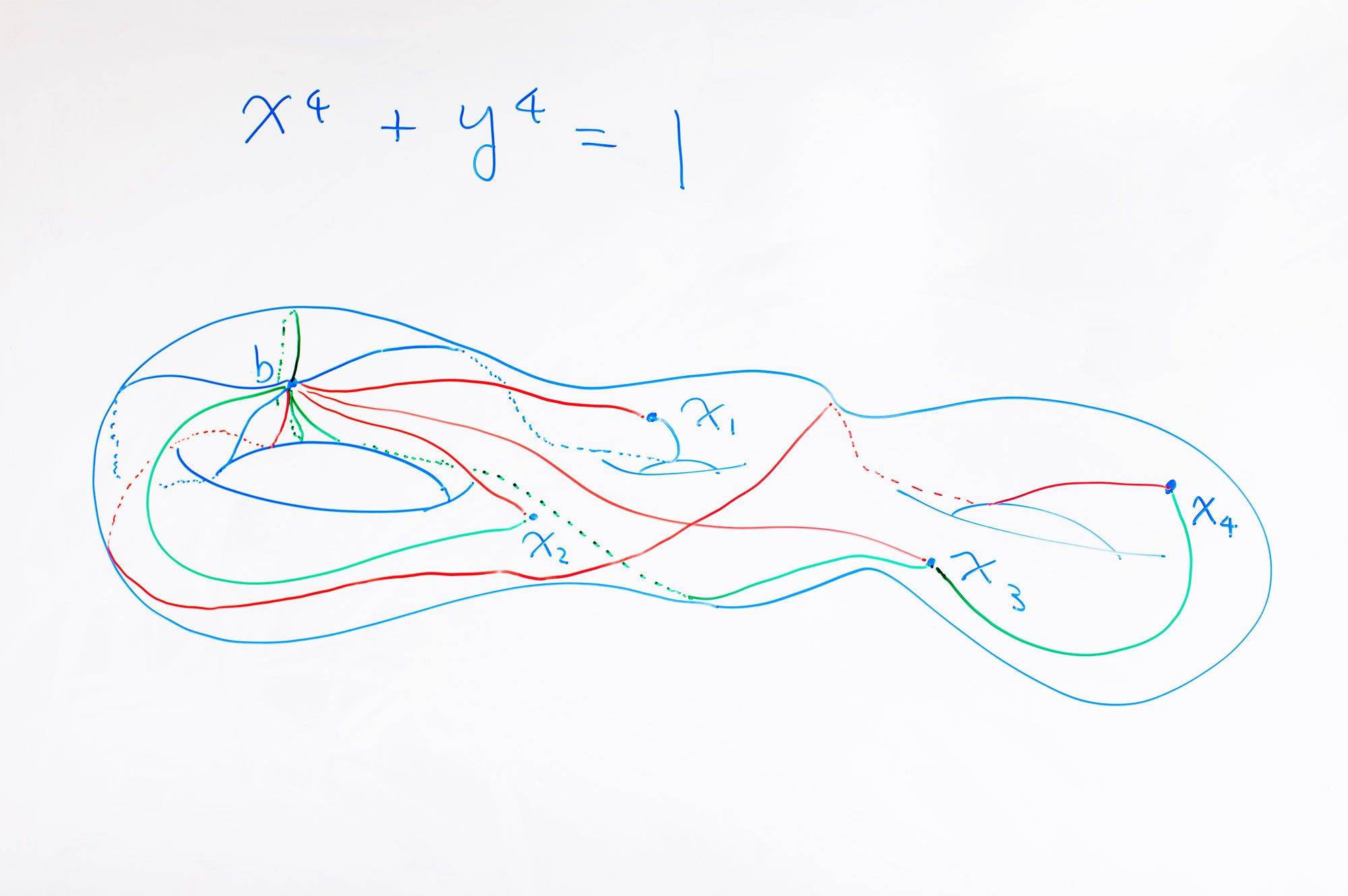
Математический объект, тор с тремя отверстиями, украшает доску Кима в Оксфордском университете.
Если эта связь кажется фантастической, то так оно и есть, даже для математиков. Поэтому Ким долго не раскрывал её подробностей. «Я прятал её, поскольку много лет меня смущала связь с физикой, — говорит он. — Специалисты по теории чисел — люди весьма практичные, и влияние физики иногда заставляет их скептически относиться к математике».
Но сейчас Ким говорит, что готов поделиться своим видением. «Я думаю, что изменения — просто симптом старения!» — написал Ким, которому исполнилось 53, в одном из первых писем, которыми мы обменялись для написания этой истории.
Недавно он провёл конференцию, на которую съехались вместе специалисты по теории чисел и теории струн. Также он набросал черновики статей, начинающих описывать его вдохновение для математического сообщества, не привыкшего размышлять о числах при помощи таких прямых аналогий с физическим миром.
Остаётся только одно препятствие — последняя часть аналогии физики в математике, которую Киму ещё предстоит проработать. Он надеется, что, пригласив других разделить его видение, особенно физиков, он получит необходимую для завершения работы помощь.
Древняя загадка
Рациональные решения уравнений активно притягивают разум человека. Они приносят удовлетворение, схожее с тем, что вы получаете от вставших на место кусочков головоломки. Поэтому они являются героями самых знаменитых математических гипотез.
К числу рациональных чисел принадлежат целые числа и любое число, которое можно выразить в виде отношения двух целых, например, 1, -4 или 99/100. Математикам особенно интересны такие рациональные числа, которые решают Диофантовы уравнения — полиномиальные уравнения с целыми коэффициентами, например, x2 + y2 = 1. Они названы в честь математика Диофанта, изучавшего их в Александрии в III веке н.э.
Рациональные решения сложно найти в общем случае, поскольку они не подчиняются никакой геометрической закономерности. Возьмём уравнение x2 + y2 = 1. Его решения в вещественных числах формируют круг. Уберите все точки на круге, которые нельзя выразить в виде дроби, и останутся только рациональные решения, не формирующие подобного аккуратного объекта. Рациональные решения выглядят случайно разбросанными по окружности.
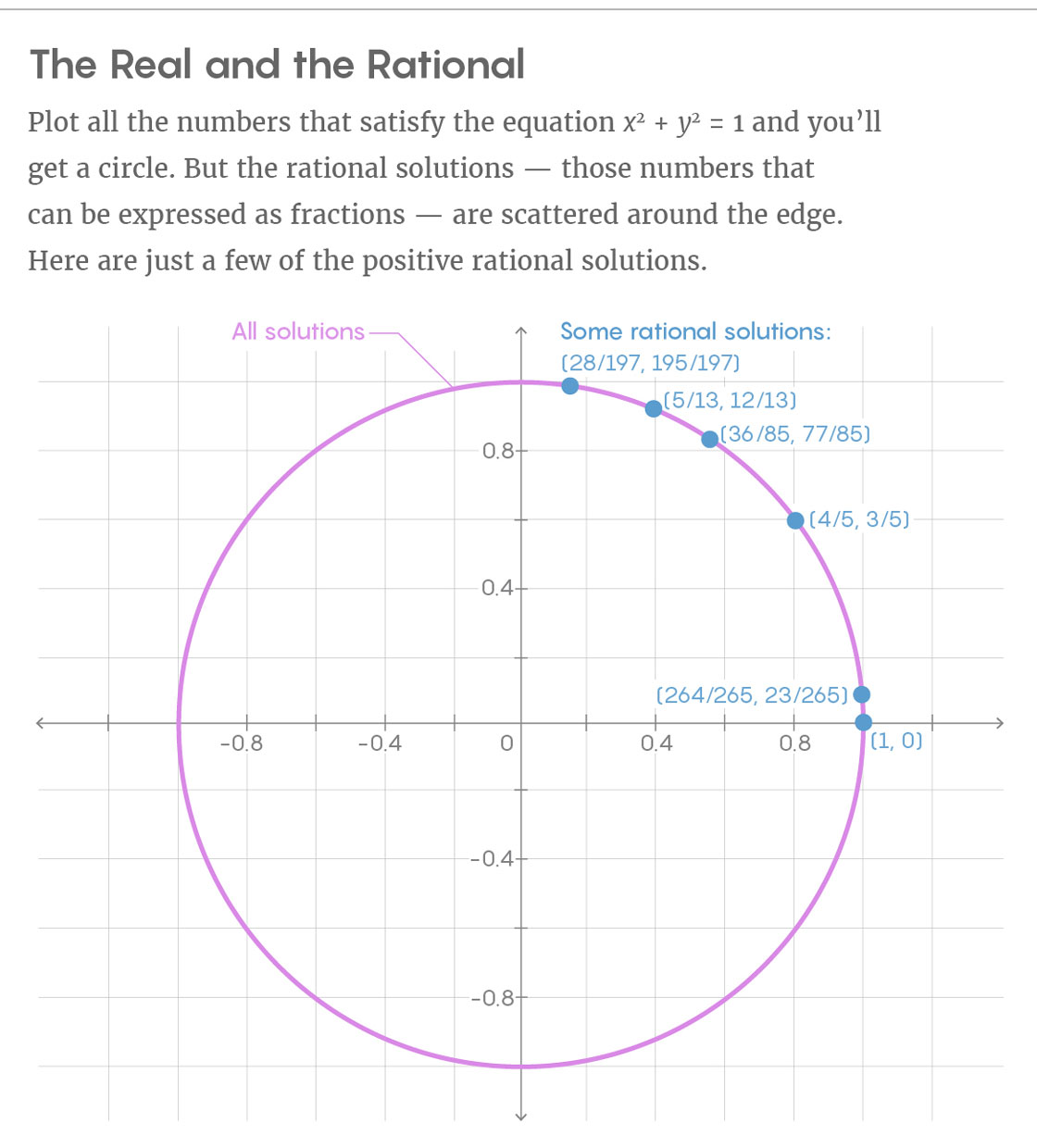
«Условие, которому должна подчиняться точка, чтобы иметь рациональные координаты, совсем не геометрическое. Невозможно записать уравнение, которому должны удовлетворять рациональные точки», — говорит Ким.
Часто довольно просто бывает найти одно рациональное решение, или даже несколько. Но математикам, не любящим недосказанность, более интересно найти все рациональные решения. А это гораздо сложнее. Настолько сложно, что, доказательства даже незначительного утверждения о количестве рациональных решений достаточно, чтобы прослыть математическим светилом. В 1986 году Герд Фальтингс выиграл Филдсовскую премию, высочайшую математическую награду, в основном за доказательство гипотезы Морделла, которая говорит, что у определённых классов диофантовых уравнений есть только конечное число рациональных решений.
Доказательство Фальтингса стало поворотным пунктом теории чисел. А также тем, что математики называют «неэффективным доказательством», поскольку оно не дало точное количество рациональных решений, и не нашло их. С тех пор математики ищут способы сделать эти, следующие шаги. Рациональные точки выглядят случайными на обычном графике уравнения. Математики надеются, что изменив контекст, в рамках которого они размышляют о проблеме, можно заставить эти точки выглядеть, как осмысленная комбинация, которую можно описать неким точным способом. Проблема в том, что известные области математики такого контекста не предоставляют.

Ким в своём офисе в Оксфорде
«Для получения эффективных результатов от рациональных точек явно ощущается необходимость в появлении новой идеи», — сказал Элленберг.
Сейчас существует два основных предположения о природе такой идеи. Одно исходит от японского математика Синъити Мотидзуки, в 2012 году опубликовавшего на странице своего факультета в Киотском университете сложную и инновационную математическую работу на несколько сотен страниц. Через пять лет эта работа так и остаётся в основном непонятной. Другая новая идея пришла от Кима, попробовавшего представлять себе рациональные числа в расширенном числовом контексте, в котором начинают проявляться их скрытые закономерности.
Симметричное решение
Математики часто говорят, что чем симметричнее объект, тем легче его изучать. Поэтому они хотели бы разместить изучение диофантовых уравнений в условиях, содержащих больше симметрии, чем те, где эта задача возникает естественным образом. Если это получится, они смогут использовать новообретённые симметрии, чтобы отследить нужные им рациональные точки.
Чтобы понять, как симметрия помогает математику ориентироваться в задаче, представьте себе круг. Возможно, ваша цель — определить все точки на круге. Симметрия сильно помогает, поскольку она создаёт карту, позволяющую вам передвигаться от известных вам точек к тем, что ещё предстоит открыть.
Представьте, что вы обнаружили все рациональные точки в нижней части окружности. Поскольку окружность обладает зеркальной симметрией, точки можно отразить вверх (меняя знаки у всех координат y) и внезапно получить все точки из верхней части. У окружности вообще настолько богатая симметрия, что для поиска всех точек на ней необходимо узнать положение лишь одной точки, а затем скомбинировать его со знаниями о симметрии круга: нужно просто применить бесконечную поворотную симметрию окружности к начальной точке.
Но если геометрический объект, с которым вы работаете, гораздо менее правильный, как, например, случайным образом виляющий путь, вам придётся очень много работать для того, чтобы определить каждую точку отдельно — у вас не будет симметричных отношений, позволяющих вам разметить неизвестные точки при помощи известных.
У числовых множеств тоже могут быть симметрии, и чем больше в множестве симметрии, тем легче его понять — можно применить симметричные взаимоотношения для обнаружения неизвестных значений. Числа с определёнными видами симметрии формируют «группу», и математики используют свойства группы, чтобы понять содержащиеся в ней числа.
Множество рациональных решений уравнения не обязано иметь симметрию и не формируют группу, из-за чего математики сталкиваются с нереальной задачей в попытках отыскать решения по одному.
С 1940-х годов математики начали изучать методы расположение диофантовых уравнений в более симметричных условиях. Математик Клод Чаботи [Claude Chabauty] открыл, что внутри более крупного геометрического пространства, созданного им (при использовании расширенной вселенной чисел под названием p-адические числа), рациональные числа формируют своё собственное симметричное подпространство. Он взял это подпространство и скомбинировал его с графиком диофантового уравнения. Точки их пересечения оказались рациональными решениями уравнения.
В 1980-х математик Роберт Коулман уточнил работу Чаботи. За последовавшие пару десятилетий подход Коулмана-Чаботи был лучшим математическим инструментом, имевшихся у математиков для поиска рациональных решений диофантовых уравнений. Но он работает только в случае, когда график уравнения соотносится с размером более крупного пространства в определённой пропорции. Когда она нарушается, становится сложно точно находить положение точек пересечения кривой уравнения и рациональных чисел.
«Если ваша кривая находится в окружающем пространстве, где есть слишком много рациональных точек, они начинают скапливаться и вам трудно различать, какие из них находятся на кривой», — говорит Киран Кедлайа [Kiran Kedlaya], математик из Калифорнийского университета в Сан-Диего.
И тут вступает Ким. Чтобы расширить работу Чаботи, он хотел найти ещё более крупное пространство, в котором можно исследовать диофантовы уравнения — пространство, где рациональные числа более разрозненны, что позволяет изучать точки пересечения с большим количеством разновидностей диофантовых уравнений.


Пространства пространств
Если вам нужно более крупное пространство и некоторые намёки на то, как можно использовать симметрию для того, чтобы в нём ориентироваться, вам подойдёт физика.
В общем случае пространство в математическом смысле — это любой набор точек с геометрической или топологической структурой. Тысяча точек, рассеянных волей-неволей, не образуют пространства — их не связывает вместе структура. Но сфера, представляющая собой связанную организацию точек, это уже пространство. Как и тор, или двухмерная плоскость, или четырёхмерное пространство-время, где мы живём.
Кроме этих, существуют ещё более экзотические пространства, которые можно представить себе, как «пространства пространств». Самый простой пример: допустим, у вас есть треугольник — и это пространство. Теперь представьте пространство всех возможных треугольников. Каждая точка в нём представляет определённый треугольник, и координаты этой точки задаются углами представляемого ею треугольника.
Такая идея часто оказывается полезной в физике. В рамках общей теории относительности пространство и время постоянно развиваются, и физики считают каждую конфигурацию пространства и времени точкой в пространстве всех конфигураций пространства-времени. Пространства пространств также появляются в области, которую физики называют калибровочная инвариантность, работающей с полями, наложенными на физическое пространство. Эти поля описывают то, как меняются силы вроде электромагнетизма и гравитации при передвижении в пространстве. Можно представить, что в каждой точке пространства конфигурация этих полей слегка отличается — и что все эти разные конфигурации формируют точки в «пространстве всех полей» более высокой размерности.
Это пространство полей из физики — аналогия, близкая к предложению Кима для теории чисел. Чтобы это понять, представьте себе луч света. Физики представляют свет, движущийся через пространство полей более высокой размерности. В этом пространстве свет пойдёт по пути, который придерживается принципа наименьшего сопротивления и минимизирует количество времени, необходимое для того, чтобы добраться из точки А в точку В. Этот принцип объясняет, почему свет изгибается при переходе из одного материала в другой — изогнутый путь минимизирует временные затраты.
Более крупные пространства пространств, появляющиеся в физике, обладают дополнительными симметриями, которых нет ни в каком из представляемых ими пространств. Эти симметрии привлекают внимание к определённым точкам, допустим, акцентируясь на пути, минимизирующем время. Те же самые симметрии, построенные другим способом и в другом контексте, могут акцентироваться на других точках — например, на точках, соответствующих рациональным решениям уравнений.
Соединяя симметрию с физикой
В теории чисел нет никаких частиц, которые можно было бы отслеживать, но в ней есть нечто вроде пространства-времени, и она предлагает способ рисовать пути и создавать пространство всех возможных путей. Из этого базового соответствия Ким разрабатывает схем, в которой «задача нахождения траектории света и нахождения рациональных решений диофантовых уравнений являются двумя гранями одной задачи», — как он объяснил на прошлой неделе на конференции по математической физике в Гейдельберге.
Решения диофантовых уравнений формируют пространства — это кривые, определяемые уравнениями. Эти кривые могут быть одномерными, как окружность, или многомерными. К примеру, если построить комплексное решение диофантового уравнения x4 + y4 = 1, получится тор с тремя отверстиями. У рациональных точек на таком торе нет геометрической структуры — именно поэтому их тяжело найти —, но их можно сопоставить с точками в многомерном пространстве пространств, такой структурой обладающими.
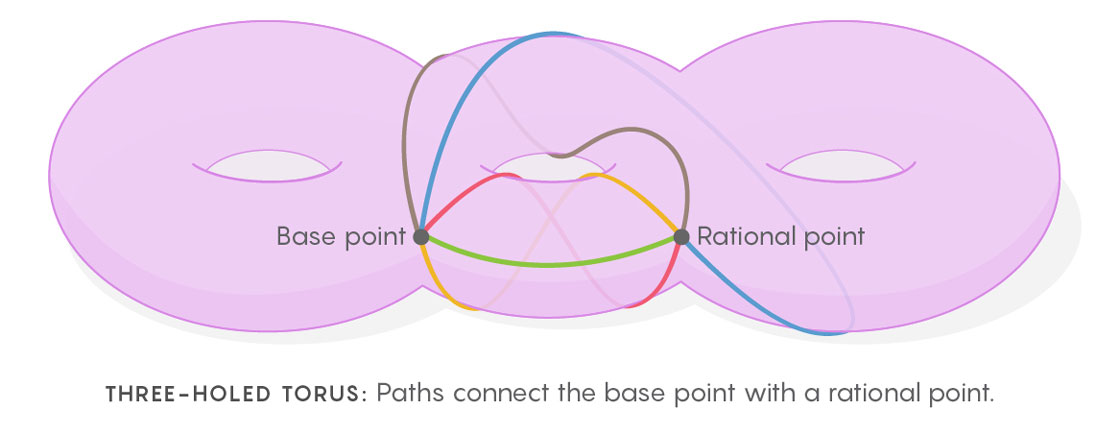
Ким создаёт это многомерное пространство пространств, представляя о том, какими способами можно нарисовать на торе замкнутые кривые (или в том пространстве, которое определяет уравнение). Процедура рисования кривых выглядит так. Сначала необходимо выбрать начальную точку, затем нарисовать петлю из этой точки в любую другую, и вернуться в первую. Теперь повторите этот процесс, рисуя пути, соединяющие базовую точку со всеми остальными точками тора. У вас получится чаща всех возможных петель, начинающихся и заканчивающихся в базовой точке. Этот набор петель — центрально важный объект математики, называющийся фундаментальной группой пространства.
Любую точку на торе можно использовать в качестве начальной. У каждой точки получится уникальная чаща путей, исходящих из неё. Каждую из таких коллекций путей можно представить в виде точки в многомерном «пространстве всех наборов путей» (как пространство всех возможных треугольников). Это пространство пространств геометрически очень похоже на то, что строят физики в теории калибровочной инвариантности: то, как наборы путей меняются, когда вы идёте от одной точки на торе к другой, сильно напоминает то, как меняются поля, когда вы идёте от одной точки к другой в реальном пространстве. Это пространство пространств обладает дополнительными симметриями, которых нет на самом торе. И хотя у рациональных точек на торе нет симметрии, если перейти в пространство всех наборов путей, можно найти симметрии между точками, связанные с рациональными числами. Вы приобретаете симметрии, которых раньше не было видно.
«Я иногда говорю, что этих путях закодирована «скрытая арифметическая симметрия», сильно аналогичная внутренним симметриям теории калибровочной инвариантности», — сказал Ким.
Как и Чаботи, Ким находит рациональные решения, исследуя точки пересечения в созданном ими более крупном пространстве. Он использует симметрии этого пространства, чтобы прийти к точкам пересечения. Он надеется разработать уравнение, точно определяющее эти точки.
В физическом контексте можно представить себе все возможные пути, которыми может пойти луч света. Это ваше «пространство всех путей». Физиков интересуют точки этого пространства, соответствующие путям, минимизирующим время. Ким считает, что у точек, соответствующим чащам путей, исходящим из рациональных точек, присуще нечто вроде такого же свойства — то есть, эти точки минимизируют некоторое свойство, возникающее, когда вы рассматриваете геометрические формы диофантовых уравнений. Он просто ещё пока не разобрался, что это может быть за свойство.
«Что я начал пытаться найти», так это принцип наименьшего сопротивления в математическом контексте, написал он мне в письме. «Я пока его не нашёл, но уверен, что он существует».
Неопределённое будущее
За последние несколько месяцев я описывал видение Кима, вдохновлённое физикой, нескольким математикам, поклонникам его вкладов в теорию чисел. Но узнав о такой подробности его работы, они терялись.
«Как теоретик представительных величин, я, если бы мне показали все те удивительные достижения, сделанные Миньоном, и спросили бы, вдохновлены ли они физикой, сказал бы: О чём вы, чёрт возьми?» — сказал Элленберг.
Пока что Ким не упоминал физику ни в одной из своих работ. Вместо этого он пишет об объектах под названием «вариации Селмера», и рассматривает связь между вариациями Селмера в пространстве всех вариаций Селмера. Такие вещи специалистам по теории чисел знакомы. Но для Кима они всегда были просто другим обозначением определённых физических объектов.
«Должен быть способ использовать физические идеи для решения задач в теории чисел, но мы пока ещё недостаточно хорошо продумали то, как создать подобную платформу, — сказал Ким. — Мы находимся в таком состоянии, когда наше понимание физики достаточно хорошо развито, и в нём заинтересовано достаточное много специалистов по теории чисел для того, чтобы сделать следующий шаг».
Основное препятствие для метода Кима находится в поиске какого-либо действия для минимизации пространства всех наборов петель. В физическом мире такой подход выглядит естественно, но в арифметике не имеет очевидного смысла. Даже математики, пристально следящие за работой Кима, не уверены, сможет ли он его найти.
«Думаю, программа Кима сделает для нас очень много всего замечательного. Не думаю, что у нас появится настолько чёткое, как хочет Миньон, понимание того, являются ли рациональные точки классическими решениями арифметической калибровочной теории», — говорит Арнав Трипати [Arnav Tripathy], профессор математической физики в Гарвардском Университете.
Сегодня язык физики практически не пересекается с практикой теории чисел. Ким считает, что это почти наверняка изменится. Сорок лет назад физика, геометрия и топологии имели мало общего. Затем в 1980-х несколько математиков и физиков, сейчас представляющие собой значительные фигуры, нашли точные способы использования физики для изучения свойств форм. После этого разработки этой области изменились и уже не возвращались к прежним методам.
«В наше время практически невозможно интересоваться геометрией и топологией, ничего не зная о физике. Я вполне уверен, что это произойдёт и с теорией чисел» в следующие 15 лет, сказал Ким. «Все связи чрезвычайно естественны».
