[Перевод] Псевдотонирование изображений: одиннадцать алгоритмов и исходники
Псевдотонирование: обзор

Про сегодняшнюю тему для программирования графики — псевдотонирование (дизеринг) — я получаю много писем, что может показаться удивительным. Вы можете подумать, что псевдотонирование — это не то, чем программисты должны заниматься в 2012 году. Разве псевдотонирование — не артефакт история технологий, архаизм времён, когда дисплей с 16 миллионами цветов программистам и пользователям мог только сниться? Почему я пишу статью о псевдотонировании в эпоху, когда дешевые мобильные телефоны работают с великолепием 32-битной графики?
На самом деле псевдотонирование по-прежнему остаётся уникальным методом не только по практическим соображениям (например, подготовка полноцветного изображения для печати на чёрно-белом принтере), но и по художественным. Дизеринг также находит применение в веб-дизайне, где этот полезный метод используется для сокращения числа цветов изображения, что уменьшает размер файла (и трафик) без ущерба для качества. Он также используется при уменьшении цифровых фотографий в формате RAW в 48 или 64 бита на пиксель до RGB в 24 бита на пиксель для редактирования.
И это — применения лишь в области изображений. В звуке дизеринг тоже играет ключевую роль, но боюсь, обсуждать здесь дизеринг аудио я не буду. Только псевдотонирование изображений.
В этой статье я собираюсь сосредоточиться на трех пунктах:
- Основные моменты работы дизеринга изображений
- Одиннадцать конкретных двухмерных формул дизеринга, в том числе известных уровня алгоритма Флойда-Стейнберга.
- Как написать движок псевдотонирования общего назначения
Псевдотонирование: примеры
Рассмотрим следующее полноцветное изображение, обои со знаменитым Кубом-Компаньоном из игры Portal:

Эта картинка будет тестовым изображением для этой статьи. Я выбрал её, потому что у неё есть отличные сочетания мягких градиентов и жестких краев.
На современном ЖК- или светодиодном дисплее — будь то монитор компьютера, смартфон или телевизор — это полноцветное изображение можно выводить без проблем. Но представим ПК постарее с поддержкой ограниченной палитры цветов. Если мы попытаемся отобразить наше изображение на таком ПК, это может выглядеть примерно так:

Это то же изображение, что и выше, но ограниченное веб-палитрой безопасных цветов.
Довольно мерзотно, не так ли? Рассмотрим еще более яркий пример, в котором мы хотим напечатать изображение куба на чёрно-белом принтере. Тогда у нас получается что-то подобное:

Здесь изображение едва узнаваемо.
Проблемы возникают каждый раз, когда изображение отображается на устройстве, которое поддерживает меньше цветов, чем содержит изображение. Тонкие градиенты в исходном изображении могут быть заменены пятнами однородного цвета, и в зависимости от ограничений устройства, исходное изображение может стать неузнаваемым.
Псевдотонирование (или дизеринг) — это попытка решить эту проблему. Псевдотонирование работает через приближённое выражение недоступных цветов доступными, для чего доступные цвета смешиваются так, чтобы имитировать недоступные. В качестве примера здесь приведено изображение куба, вновь ухудшенное до цветов воображаемого старого ПК, только на этот раз применено псевдотонирование:

Значительно лучше, чем в версии без псевдотонирования!
Если вы внимательно посмотрите, вы увидите, что это изображение использует те же цвета, что и его копия без псевдотонирования. Но эти несколько цветов расположены так, что кажется, будто присутствует много других цветов.
В качестве другого примера: здесь чёрно-белая версия нашего изображения с похожим псевдотонированием:

Если говорить конкретно, то здесь применено псевдотонирование по двухрядном алгоритму Сьерры (2-row Sierra).
Несмотря на наличие только чёрного и белого цветов, мы всё ещё можем различить форму куба вплоть до сердец с обеих сторон. Дизеринг — чрезвычайно мощный метод, и его можно использовать в ЛЮБОЙ ситуации, когда данные должны быть представлены в более низком разрешении, чем то, для которого их создавали. В этой статье основное внимание будет уделено изображениям, но те же методы могут быть применены к любым двухмерным данным (или к одномерным данным, что еще проще!).
Основная концепция псевдотонирования
Если коротко, псевдотонирование в корне связано с рассеиванием ошибок.
Рассеивание ошибок работает следующим образом: предположим, что нам нужно свести фотографию в градациях серого до чёрных и белых цветов, чтобы мы могли напечатать её на принтере, который поддерживает только чистый черный (чернила) или чистый белый (бумага без чернил) цвет. Первый пиксель на изображении — тёмно-серый, со значением 96 по шкале от 0 до 255, где 0 — чистый чёрный цвет, 255 — чистый белый.
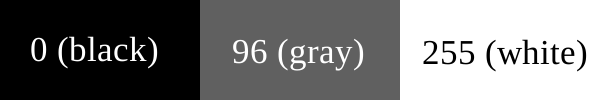
Визуализация значений RGB в нашем примере.
При преобразовании такого пикселя в черный или белый мы используем простую формулу: значение цвета ближе к 0 (черному) или 255 (белому)? 96 ближе к 0, чем к 255, поэтому мы делаем пиксель черным.
На этом этапе стандартный подход — просто перемещаться к следующему пикселю и выполнять то же сравнение. Но проблема возникает, если у нас есть куча подобных серых пикселей со значением 96 — все они превращаются в чёрные. У нас получается с огромный кусок пустых черных пикселей, которые плохо представляют оригинальный серый цвет.
Рассеивание ошибок следует более умному подходу к проблеме. Как вы могли предположить, рассеивание ошибок работает путем «рассеивания» — или распространения — ошибки каждого вычисления в соседние пиксели. Если алгоритм находит серый пиксель со значением 96, он также определяет, что 96 ближе к 0, чем к 255 — и поэтому делает пиксель черным. Но тогда алгоритм учитывает «ошибку» в его преобразовании. В частности, ошибку в том, что серый пиксель, который мы заставили быть черным, на самом деле был на расстоянии в 96 шагов от черного.
Когда он перемещается к следующему пикселю, алгоритм рассеивания ошибок добавляет ошибку предыдущего пикселя к текущему пикселю. Если следующий пиксель также имеет серый цвет 96, вместо того, чтобы сделать его черным, алгоритм добавляет ошибку 96 из предыдущего пикселя. Это приводит к значению 192, которое на самом деле ближе к 255 — и, следовательно, ближе к белому! Таким образом, алгоритм делает этот пиксель белым и снова учитывает ошибку. В этом случае ошибка составляет −63, потому что 192 на 63 меньше, чем 255 — то значение, на которое этот пиксель поменяли.
По мере того, как алгоритм продолжает работу, рассеивание ошибок приводит к чередованию черных и белых пикселей, что довольно хорошо имитирует серый цвет значения 96 этого сегмента. Это куда лучше, чем окрашивать все пиксели подряд чёрным. Как правило, когда мы заканчиваем обработку строки изображения, мы отбрасываем значение ошибки, которое мы отслеживали, и начинаем заново с ошибкой »0» со следующей строки изображения.
Ниже приведен пример изображения нашего куба с применением описанного алгоритма. В частности, каждый пиксель преобразуется в черный или белый, ошибка преобразования отмечается и передается следующему пикселю справа:

Это самое простое применение псевдотонирования с рассеиванием ошибок.
К сожалению, псевдотонирование с рассеиванием ошибок имеет свои собственные проблемы. Как бы то ни было, псевдотонирование всегда приводит к заметным точкам или к пунктирному виду. Это неизбежный побочный эффект работы с небольшим количеством доступных цветов — из-за их количества эти цвета будут повторяться снова и снова.
В приведенном выше простом примере алгоритма рассеивания ошибок очевидна другая проблема — если у вас есть блок очень похожих цветов, и вы толкаете ошибку только вправо, все «точки» оказываются в одном и том же месте! Это приводит к забавным линиям точек, которые почти так же отвлекают, как и оригинальная версия без псевдотонирования.
Проблема в том, что мы используем только одномерное рассеивание ошибок. Распространив ошибку только в одном направлении (вправо), мы не очень хорошо её распределяем. Поскольку у изображения измерения два (горизонтальное и вертикальное), почему бы не направить ошибку в нескольких направлениях? Это распределит ошибку более равномерно, что, в свою очередь, позволит избежать странных линий точек, рассмотренных в примере рассеивания ошибок выше.
Псевдотонирование с двухмерным рассеиванием ошибок
Существует много способов рассеивания ошибки в двух измерениях. Например, мы можем распространить ошибку на один или несколько пикселей вправо, влево, вверх и вниз.
Для простоты расчетов все стандартные формулы дизеринга продвигают ошибку только вперед. Если обойти изображение попиксельно, начиная с верхнего левого угла и двигаясь вправо, учитывать ошибки назад (например, влево и/или вверх) необходимости не будет. Причина этого очевидна — если закидывать ошибку назад, придётся вернуться к пикселям, которые уже обработаны, что приводит к большему количеству ошибок при движении назад. В итоге получится бесконечный цикл распространения ошибок.
Таким образом, для стандартного поведения цикла (начиная с верхнего левого угла изображения и двигаясь вправо) мы хотим, чтобы движение пикселей шло только вправо и вниз.

Извиняюсь за паршивое изображение —, но я надеюсь, что это поможет проиллюстрировать суть правильного распространения ошибок.
Что же касается конкретных способов распространения ошибки, над этой задачей билось много людей умнее меня. Позвольте мне поделиться этими формулами с вами.
(Примечание: эти формулы дизеринга доступны на нескольких сайтах в Интернете, но наиболее полный справочник из всего, что я нашел — этот.)
Алгоритм рассеивания ошибок Флойда-Стейнберга
Первая и возможно самая известная формула рассеивания ошибок была опубликована Робертом Флойдом и Луисом Стейнбергом в 1976 году. Рассеивание ошибок происходит по следующей схеме:
X 7
3 5 1
(1/16)
В приведенных выше обозначениях X означает текущий пиксель. Дробь в нижней части представляет собой делитель для ошибки. Иначе говоря, формула Флойда-Стейнберга может быть записана в виде:
X 7/16
3/16 5/16 1/16
Но такое обозначение длинное и неаккуратное, поэтому я буду придерживаться оригинала.
Вернёмся к нашему оригинальному примеру преобразования пиксельного значения от 96 к 0 (чёрный) или к 255 (белый). При окрашивании пикселя в чёрный мы получаем ошибку 96. Мы распространяем эту ошибку окружающим пикселям, поделив 96 на 16 (= 6), затем умножаем её на соответствующие значения, например:
X +42
+18 +30 +6
Путем распространения ошибки нескольким пикселям, каждому с различным значением, мы сводим к минимуму все отвлекающие полосы с точками, заметные в исходном примере алгоритма рассеивания ошибок. Вот изображение куба с применением алгоритма Флойда-Стейнберга:

Алгоритм рассеивания ошибок Флойда-Стейнберга
Неплохо, а?
Алгоритм рассеивания ошибок Флойда-Стейнберга — вероятно, наиболее известный алгоритм рассеивания ошибок. Он даёт достаточно хорошее качество, а также требует только один передний массив (одномерный массив шириной в изображение, где хранятся значения ошибок, распространяемые к следующей строке). Кроме того, поскольку его делитель 16, вместо деления можно использовать битовые сдвиги. Так алгоритм достигает высокой скорости работы даже на старом оборудовании.
Что касается значений ⅓/5/7, используемых для распространения ошибки — они были выбраны специально, потому что они создают равномерный клетчатый узор для серого изображения. Умно!
Одно предупреждение по поводу алгоритма Флойда-Стейнберга — некоторые программы могут использовать и другие, более простые формулы псевдотонирования и называть их «Флойд-Стейнберг», надеясь, что люди не знают разницы. Вот отличная статья о дизеринге, которая описывает один из таких «ложных алгоритмов Флойда-Стейнберга»:
X 3
3 2
(1/8)
Этот упрощение оригинального алгоритма Флойда-Стейнберга даёт не только заметно худший результат, но и делает это без каких-либо значимых преимуществ с точки зрения скорости (или памяти, так как массив для хранения значений ошибки для следующей строки всё ещё требуется).
Но если вам интересно, вот изображение куба после прохода «ложного Флойда-Стейнберга»:

Гораздо больше скоплений точек, чем в настоящем алгоритме Флойда-Стейнберга — так что не используйте эту формулу!
Алгоритм Джарвиса, Джудиса и Нинке (Jarvis, Judice, Ninke)
В год, когда Флойд и Стейнберг опубликовали свой знаменитый алгоритм дизеринга, был издан менее известный, но гораздо более мощный алгоритм. Фильтр Джарвиса, Джудиса и Нинке значительно сложнее, чем Флойда-Стейнберга:
X 7 5
3 5 7 5 3
1 3 5 3 1
(1/48)
При таком алгоритме ошибка распределяется на в три раза больше пикселей, чем у Флойда-Стейнберга, что приводит к более гладкому и более тонкому результату. К сожалению, делитель 48 не является степенью двойки, поэтому битовые сдвиги применить не удастся. Используются только значения 1/48, 3/48, 5/48, и 7/48, так что эти значения могут быть вычислены единожды, а затем размножены несколько раз для небольшого увеличения по скорости.
Другим недостатком фильтра JJN является то, что он толкает ошибку вниз не на одну строку, а на две. Это означает, что нам нужны два массива — один для следующей строки, второй для строки после неё. Это было проблемой в то время, когда алгоритм был впервые опубликован, но на современных ПК и смартфонах это дополнительное требование не имеет никакого значения. Честно говоря, может быть лучше использовать единый массив ошибки размером с изображение, а не стирать две однорядные решетки снова и снова.

Псевдотонирование Джарвиса, Джудиса и Нинке
Дизеринг Штуки (Stucki)
Через пять лет после публикации формулы дизеринга Джарвиса, Джудиса и Нинке Питер Штуки опубликовал скорректированную версию с небольшими изменениями для улучшения времени обработки:
X 8 4
2 4 8 4 2
1 2 4 2 1
(1/42)
Степенью двойки делитель 42 не является, а вот значения рассеивания ошибки — да. Поэтому ошибка делится на 42, сдвиги по битам могут быть использованы для получения конкретных значений для рассеивания.
Для большинства изображений разница между алгоритмами Штуки и JJN будет минимальна. Поэтому первый чаще используется из-за его небольшого преимущества в скорости.

Псевдотонирование Штуки
Дизеринг Аткинсона
В середине 1980-х годов псевдотонирование становится все более популярным, поскольку аппаратное обеспечение компьютеров доросло до поддержки более мощных драйверов видеоадаптера и дисплея. Один из лучших алгоритмов дизеринга той эпохи разработал Билл Аткинсон, сотрудник компании Apple, который работал над всем: от MacPaint (который он писал с нуля для оригинального Macintosh) до HyperCard и QuickDraw.
Формула Аткинсона немного отличается от других в этом списке, потому что она распространяет только часть ошибки, не всю целиком. В современных графичесих приложениях этот метод встречается под именем «уменьшить выцветание». Рассеивание только части ошибок помогает уменьшить зернистость, но непрерывные светлые и темные участки изображения могут потерять цвет.
X 1 1
1 1 1
1
(1/8)

Псевдотонирование Аткинсона
Псевдотонирование Бёркеса (Burkes)
Через семь лет после того, как Штуки опубликовал улучшения алгоритма Джарвиса, Джудиса и Нинке, Дэниэл Бёркес предложил дальнейшее развитие:
X 8 4
2 4 8 4 2
(1/32)
Предложение Бёркеса заключалось в том, чтобы в алгоритме Штуки опустить нижний ряд матрицы. Это не только устранило необходимость в двух массивах, но и в результате привело к делителю, вновь кратному 2. Это изменение означало, что вся математика, участвующая в вычислении ошибки, могла быть выполнена простым битовым сдвигом, причем с незначительной потерей качества.

Псевдотонирование Бёркеса
Псевдотонирование Сьерры (Sierra)
Последние три алгоритма дизеринга были созданы Фрэнком Сьеррой, который опубликовал следующие матрицы в 1989 и 1990 годах:
X 5 3
2 4 5 4 2
2 3 2
(1/32)
X 4 3
1 2 3 2 1
(1/16)
X 2
1 1
(1/4)
Эти три фильтра обычно называются Sierra, Two-Row Sierra (двухрядный алгоритм Сьерры) и Sierra Lite. Их конечное изображение на тестовой картинке куба выглядит следующим образом:

Sierra (иногда называют Sierra-3)

Two-row Sierra (двухрядный алгоритм Сьерры)

Sierra Lite
Остальные соображения по псевдотонированию
Если вы сравните изображения выше с результатами псевдотонирования другой программы, вы можете обнаружить небольшие различия. Подобное ожидаемо. Есть на удивление много переменных, которые могут повлиять на точность вывода алгоритма псевдотонирования. В их числе:
- Отслеживание ошибок числами с плавающей запятой или целыми числами. Целочисленные методы теряют некоторое разрешение из-за ошибок квантования.
- Уменьшение обесцвечивания. Некоторое программное обеспечение уменьшает погрешность по заданному значению (возможно, 50% или 75%), чтобы уменьшить объём обесцвечивания соседних пикселей.
- Порог отсечения для чёрного или белого. Значения 127 или 128 являются общепринятыми, но на некоторых изображениях может быть полезно использовать другие значения.
- Для цветных изображений играет важную роль то, как рассчитывается яркость. Я использую формулу яркости HSL ([max (R, G, B) + min (R, G, B)] / 2). Другие используют ([r+g+b] / 3) или одну из формул ITU. YUV или CIELAB позволят достичь результатов ещё лучше.
- Гамма-коррекция или другие предварительные модификации. Часто полезно нормализовать изображение перед его преобразованием в чёрно-белое. Выбор метода для этого очевидным образом повлияет на результат.
- Направление цикла. Я обсуждал стандартный подход «слева направо, сверху вниз», но некоторые умные алгоритмы дизеринга будут следовать змееподобному пути, где направленность слева направо меняется на противоположную. Так можно уменьшить пятна однородных точек и дать более разнообразный внешний вид, но их сложнее реализовать.
Для демонстрационных изображений в этой статье я не выполнял предварительную обработку исходного изображения. Все цветовые соответствия выполняются в пространстве RGB с отсечкой 127 (значения <= 127 установлены на 0). Направление цикла — стандартные слева направо сверху вниз.
Какие конкретные методы вы можете использовать, зависит от вашего языка программирования, ограничений обработки и желаемого результата.
Я насчитал 9 алгоритмов, но вы обещали 11! Где еще два?
До сих пор я сосредоточился исключительно на псевдотонировании на рассеивании ошибок, поскольку этот метод предлагает результаты лучше, чем статические недиффузионные алгоритмы.
Но для полноты картины вот два стандартных метода псевдотонирования с упорядоченным размытием. Псевдотонирование с упорядоченным размытием приводит к куда большему количеству точек (и худшим результатам), чем псевдотонирование с рассеиванием ошибок, но оно не требует массивов следующих строк и работает очень быстро. Для получения дополнительной информации о псевдотонировании с упорядоченным размытием посмотрите соответствующую статью в «Википедии».

Псевдотонирование с упорядоченным размытием с матрицей 4×4

Псевдотонирование с упорядоченным размытием с матрицей 8×8
С учетом этих методов статья описывает 11 различных алгоритмов псевдотонирования.
