[Перевод] Простое объяснение алгоритмов поиска пути и A*
Часть 1. Общий алгоритм поиска
Введение
Поиск пути — это одна из тех тем, которые обычно представляют самые большие сложности для разработчиков игр. Особенно плохо люди понимают алгоритм A*, и многим кажется, что это какая-то непостижимая магия.
Цель данной статьи — объяснить поиск пути в целом и A* в частности очень понятным и доступным образом, положив таким образом конец распространённому заблуждению о том, что эта тема сложна. При правильном объяснении всё достаточно просто.
Учтите, что в статье мы будем рассматривать поиск пути для игр; в отличие от более академических статей, мы опустим такие алгоритмы поиска, как поиск в глубину (Depth-First) или поиск в ширину (Breadth-First). Вместо этого мы постараемся как можно быстрее дойти от нуля до A*.
В первой части мы объясним простейшие концепции поиска пути. Разобравшись с этими базовыми концепциями, вы поймёте, что A* на удивление очевиден.
Простая схема
Хотя вы сможете применять эти концепции и к произвольным сложным 3D-средам, давайте всё-таки начнём с чрезвычайно простой схемы: квадратной сетки размером 5×5. Для удобства я пометил каждую ячейку заглавной буквой.

Простая сетка.
Самое первое, что мы сделаем — это представим эту среду в виде графа. Я не буду подробно объяснять, что такое граф; если говорить просто, то это набор кружков, соединённых стрелками. Кружки называются «узлами», а стрелки — «рёбрами».
Каждый узел представляет собой «состояние», в котором может находиться персонаж. В нашем случае состояние персонажа — это его позиция, поэтому мы создаём по одному узлу для каждой ячейки сетки:

Узлы, обозначающие ячейки сетки.
Теперь добавим рёбра. Они обозначают состояния, которых можно «достичь» из каждого заданного состояния; в нашем случае мы можем пройти из любой ячейки в соседнюю, за исключением заблокированных:

Дуги обозначают допустимые перемещения между ячейками сетки.
Если мы можем добраться из A в B, то говорим, что B является «соседним» с A узлом.
Стоит заметить, что рёбра имеют направление; нам нужны рёбра и из A в B, и из B в A. Это может показаться излишним, но не тогда, когда могут возникать более сложные «состояния». Например, персонаж может упасть с крыши на пол, но не способен допрыгнуть с пола на крышу. Можно перейти из состояния «жив» в состояние «мёртв», но не наоборот. И так далее.
Пример
Допустим, мы хотим переместиться из A в T. Мы начинаем с A. Можно сделать ровно два действия: пройти в B или пройти в F.
Допустим, мы переместились в B. Теперь мы можем сделать два действия: вернуться в A или перейти в C. Мы помним, что уже были в A и рассматривали варианты выбора там, так что нет смысла делать это снова (иначе мы можем потратить весь день на перемещения A → B → A → B…). Поэтому мы пойдём в C.
Находясь в C, двигаться нам некуда. Возвращаться в B бессмысленно, то есть это тупик. Выбор перехода в B, когда мы находились в A, был плохой идеей; возможно, стоит попробовать вместо него F?
Мы просто продолжаем повторять этот процесс, пока не окажемся в T. В этот момент мы просто воссоздадим путь из A, вернувшись по своим шагам. Мы находимся в T; как мы туда добрались? Из O? То есть конец пути имеет вид O → T. Как мы добрались в O? И так далее.
Учтите, что на самом деле мы не движемся; всё это было лишь мысленным процессом. Мы продолжаем стоять в A, и не сдвинемся из неё, пока не найдём путь целиком. Когда я говорю «переместились в B», то имею в виду «представьте, что мы переместились в B».
Общий алгоритм
Этот раздел — самая важная часть всей статьи. Вам абсолютно необходимо понять его, чтобы уметь реализовывать поиск пути; остальное (в том числе и A*) — это просто детали. В этом разделе вы будете разбираться, пока не поймёте смысл.
К тому же этот раздел невероятно прост.
Давайте попробуем формализовать наш пример, превратив его в псевдокод.
Нам нужно отслеживать узлы, которых мы знаем как достичь из начального узла. В начале это только начальный узел, но в процессе «исследования» сетки мы будем узнавать, как добираться до других узлов. Давайте назовём этот список узлов reachable:
reachable = [start_node]
Также нам нужно отслеживать уже рассмотренные узлы, чтобы не рассматривать их снова. Назовём их explored:
explored = []
Дальше я изложу ядро алгоритма: на каждом шаге поиска мы выбираем один из узлов, который мы знаем, как достичь, и смотрим, до каких новых узлов можем добраться из него. Если мы определим, как достичь конечного (целевого) узла, то задача решена! В противном случае мы продолжаем поиск.
Так просто, что даже разочаровывает? И это верно. Но из этого и состоит весь алгоритм. Давайте запишем его пошагово псевдокодом.
Мы продолжаем искать, пока или не доберёмся до конечного узла (в этом случае мы нашли путь из начального в конечный узел), или пока у нас не закончатся узлы, в которых можно выполнять поиск (в таком случае между начальным и конечным узлами пути нет).
while reachable is not empty:
Мы выбираем один из узлов, до которого знаем, как добраться, и который пока не исследован:
node = choose_node(reachable)
Если мы только что узнали, как добраться до конечного узла, то задача выполнена! Нам просто нужно построить путь, следуя по ссылкам previous обратно к начальному узлу:
if node == goal_node:
path = []
while node != None:
path.add(node)
node = node.previous
return path
Нет смысла рассматривать узел больше одного раза, поэтому мы будем это отслеживать:
reachable.remove(node)
explored.add(node)
Мы определяем узлы, до которых не можем добраться отсюда. Начинаем со списка узлов, соседних с текущим, и удаляем те, которые мы уже исследовали:
new_reachable = get_adjacent_nodes(node) - explored
Мы берём каждый из них:
for adjacent in new_reachable:
Если мы уже знаем, как достичь узла, то игнорируем его. В противном случае добавляем его в список reachable, отслеживая, как в него попали:
if adjacent not in reachable:
adjacent.previous = node # Remember how we got there.
reachable.add(adjacent)
Нахождение конечного узла — это один из способов выхода из цикла. Второй — это когда reachable становится пустым: у нас закончились узлы, которые можно исследовать, и мы не достигли конечного узла, то есть из начального в конечный узел пути нет:
return None
И… на этом всё. Это весь алгоритм, а код построения пути выделен в отдельный метод:
function find_path (start_node, end_node):
reachable = [start_node]
explored = []
while reachable is not empty:
# Choose some node we know how to reach.
node = choose_node(reachable)
# If we just got to the goal node, build and return the path.
if node == goal_node:
return build_path(goal_node)
# Don't repeat ourselves.
reachable.remove(node)
explored.add(node)
# Where can we get from here?
new_reachable = get_adjacent_nodes(node) - explored
for adjacent in new_reachable:
if adjacent not in reachable
adjacent.previous = node # Remember how we got there.
reachable.add(adjacent)
# If we get here, no path was found :(
return None
Вот функция, которая строит путь, следуя по ссылкам previous обратно к начальному узлу:
function build_path (to_node):
path = []
while to_node != None:
path.add(to_node)
to_node = to_node.previous
return path
Вот и всё. Это псевдокод каждого алгоритма поиска пути, в том числе и A*.
Перечитывайте этот раздел, пока не поймёте, как всё работает, и, что более важно, почему всё работает. Идеально будет нарисовать пример вручную на бумаге, но можете и посмотреть интерактивное демо:
Интерактивное демо
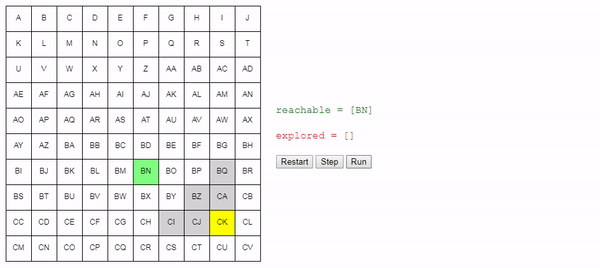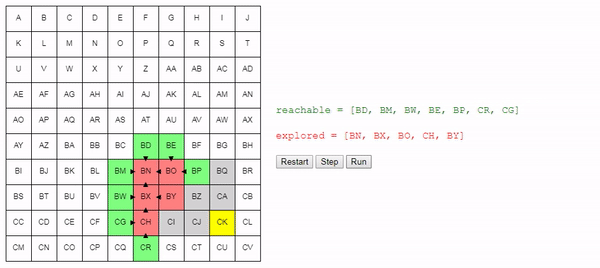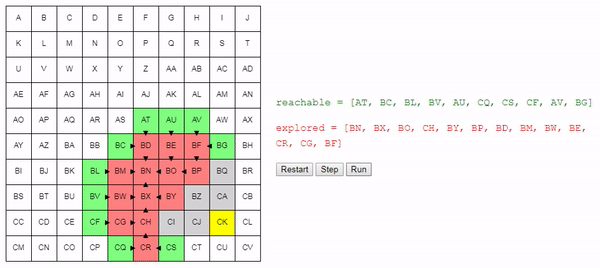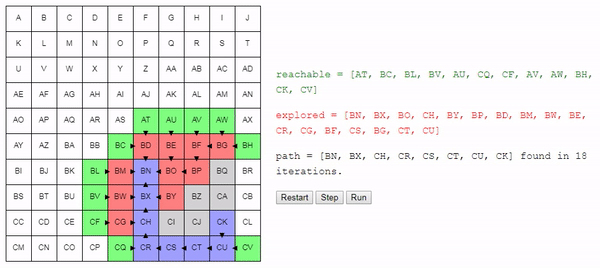
Вот демо и пример реализации показанного выше алгоритма (запустить его можно на странице оригинала статьи). choose_node просто выбирает случайный узел. Можете запустить алгоритм пошагово и посмотреть на список узлов reachable и explored, а также на то, куда указывают ссылки previous.
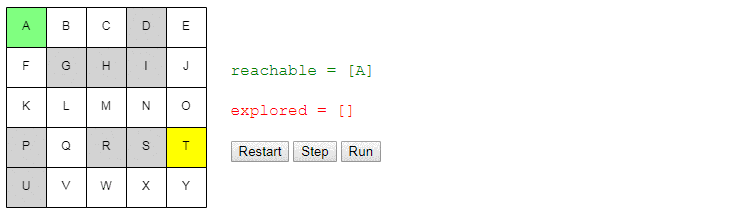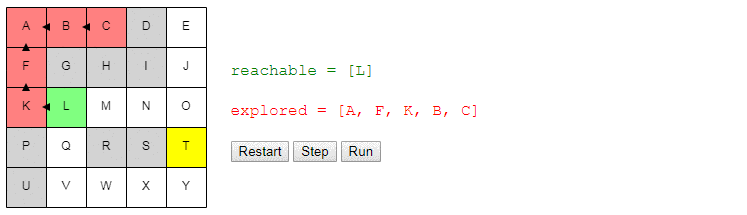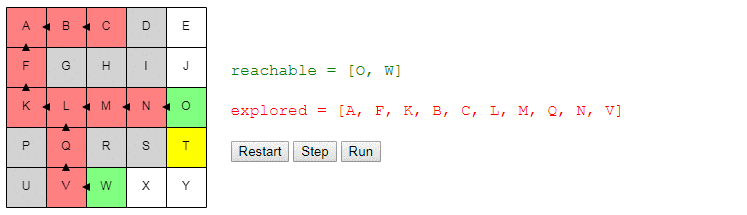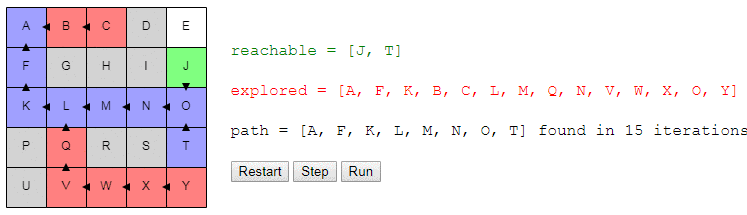
Заметьте, что поиск завершается, как только обнаруживается путь; может случиться так, что некоторые узлы даже не будут рассмотрены.
Заключение
Представленный здесь алгоритм — это общий алгоритм для любого алгоритма поиска пути.
Но что же отличает каждый алгоритм от другого, почему A* — это A*?
Вот подсказка: если запустить поиск в демо несколько раз, то вы увидите, что алгоритм на самом деле не всегда находит один и тот же путь. Он находит какой-то путь, и этот путь необязательно является кратчайшим. Почему?
Часть 2. Стратегии поиска
Если вы не полностью поняли описанный в предыдущем разделе алгоритм, то вернитесь к нему и прочтите заново, потому что он необходим для понимания дальнейшей информации. Когда вы в нём разберётесь, A* покажется вам совершенно естественным и логичным.
Секретный ингредиент
В конце предыдущей части я оставил открытыми два вопроса: если каждый алгоритм поиска использует один и тот же код, почему A* ведёт себя как A*? И почему демо иногда находит разные пути?
Ответы на оба вопроса связаны друг с другом. Хоть алгоритм и хорошо задан, я оставил нераскрытым один аспект, и как оказывается, он является ключевым для объяснения поведения алгоритмов поиска:
node = choose_node(reachable)
Именно эта невинно выглядящая строка отличает все алгоритмы поиска друг от друга. От способа реализации choose_node зависит всё.
Так почему же демо находит разные пути? Потому что его метод choose_node выбирает узел случайным образом.
Длина имеет значение
Прежде чем погружаться в различия поведений функции choose_node, нам нужно исправить в описанном выше алгоритме небольшой недосмотр.
Когда мы рассматривали узлы, соседние с текущим, то игнорировали те, которые уже знаем, как достичь:
if adjacent not in reachable:
adjacent.previous = node # Remember how we got there.
reachable.add(adjacent)
Это ошибка: что если мы только что обнаружили лучший способ добраться до него? В таком случае необходимо изменить ссылку previous узла, чтобы отразить этот более короткий путь.
Чтобы это сделать, нам нужно знать длину пути от начального узла до любого достижимого узла. Мы назовём это стоимостью (cost) пути. Пока примем, что перемещение из узла в один из соседних узлов имеет постоянную стоимость, равную 1.
Прежде чем начинать поиск, мы присвоим значению cost каждого узла значение infinity; благодаря этому любой путь будет короче этого. Также мы присвоим cost узла start_node значение 0.
Тогда вот как будет выглядеть код:
if adjacent not in reachable:
reachable.add(adjacent)
# If this is a new path, or a shorter path than what we have, keep it.
if node.cost + 1 < adjacent.cost:
adjacent.previous = node
adjacent.cost = node.cost + 1
Одинаковая стоимость поиска
Давайте теперь рассмотрим метод choose_node. Если мы стремимся найти кратчайший возможный путь, то выбирать узел случайным образом — не самая лучшая идея.
Лучше выбирать узел, которого мы можем достичь из начального узла по кратчайшему пути; благодаря этому мы в общем случае будем предпочитать длинным путям более короткие. Это не значит, что более длинные пути не будут рассматриваться вовсе, это значит, что более короткие пути будут рассматриваться первыми. Так как алгоритм завершает работу сразу после нахождения подходящего пути, это должно позволить нам находить короткие пути.
Вот возможный пример функции choose_node:
function choose_node (reachable):
best_node = None
for node in reachable:
if best_node == None or best_node.cost > node.cost:
best_node = node
return best_node
Интуитивно понятно, что поиск этого алгоритма расширяется «радиально» от начального узла, пока не достигнет конечного. Вот интерактивное демо такого поведения:
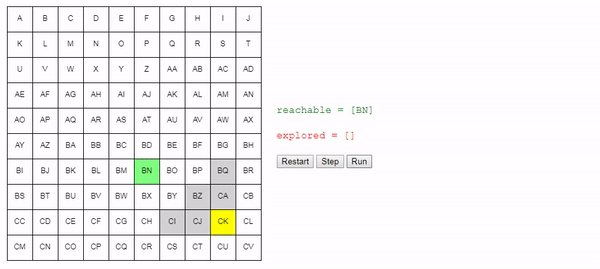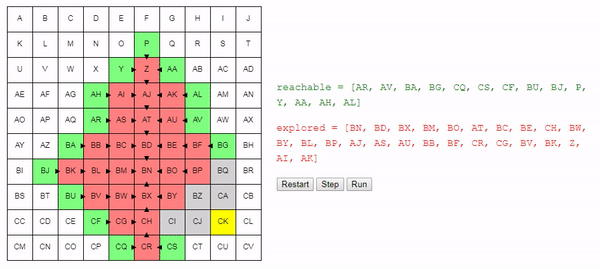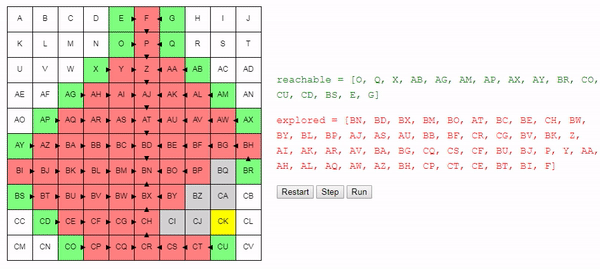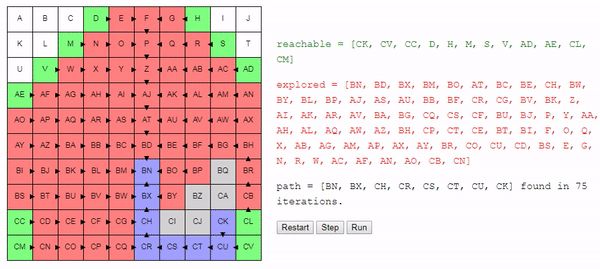
Заключение
Простое изменение в способе выбора рассматриваемого следующим узла позволило нам получить достаточно хороший алгоритм: он находит кратчайший путь от начального до конечного узла.
Но этот алгоритм всё равно в какой-то степени остаётся «глупым». Он продолжает искать повсюду, пока не наткнётся на конечный узел. Например, какой смысл в показанном выше примере выполнять поиск в направлении A, если очевидно, что мы отдаляемся от конечного узла?
Можно ли сделать choose_node умнее? Можем ли мы сделать так, чтобы он направлял поиск в сторону конечного узла, даже не зная заранее правильного пути?
Оказывается, что можем — в следующей части мы наконец-то дойдём до choose_node, позволяющей превратить общий алгоритм поиска пути в A*.
Часть 3. Снимаем завесу тайны с A*
Полученный в предыдущей части алгоритм достаточно хорош: он находит кратчайший путь от начального узла до конечного. Однако, он тратит силы впустую: рассматривает пути, которые человек очевидно назовёт ошибочными — они обычно удаляются от цели. Как же этого можно избежать?
Волшебный алгоритм
Представьте, что мы запускаем алгоритм поиска на особом компьютере с чипом, который может творить магию. Благодаря этому потрясающему чипу мы можем выразить choose_node очень простым способом, который гарантированно создаст кратчайший путь, не теряя времени на исследование частичных путей, которые никуда не ведут:
function choose_node (reachable):
return magic(reachable, "любой узел, являющийся следующим на кратчайшем пути")
Звучит соблазнительно, но магическим чипам всё равно требуется какой-то низкоуровневый код. Вот какой может быть хорошая аппроксимация:
function choose_node (reachable):
min_cost = infinity
best_node = None
for node in reachable:
cost_start_to_node = node.cost
cost_node_to_goal = magic(node, "кратчайший путь к цели")
total_cost = cost_start_to_node + cost_node_to_goal
if min_cost > total_cost:
min_cost = total_cost
best_node = node
return best_node
Это отличный способ выбора следующего узла: вы выбираем узел, дающий нам кратчайший путь от начального до конечного узла, что нам и нужно.
Также мы минимизировали количество используемой магии: мы точно знаем, какова стоимость перемещения от начального узла к каждому узлу (это node.cost), и используем магию только для предсказания стоимости перемещения от узла к конечному узлу.
Не магический, но довольно потрясающий A*
К сожалению, магические чипы — это новинка, а нам нужна поддержка и устаревшего оборудования. БОльшая часть кода нас устраивает, за исключением этой строки:
# Throws MuggleProcessorException
cost_node_to_goal = magic(node, "кратчайший путь к цели")
То есть мы не можем использовать магию, чтобы узнать стоимость ещё не исследованного пути. Ну ладно, тогда давайте сделаем прогноз. Будем оптимистичными и предположим, что между текущим и конечным узлами нет ничего, и мы можем просто двигаться напрямик:
cost_node_to_goal = distance(node, goal_node)
Заметьте, что кратчайший путь и минимальное расстояние разные: минимальное расстояние подразумевает, что между текущим и конечным узлами нет совершенно никаких препятствий.
Эту оценку получить достаточно просто. В наших примерах с сетками это расстояние городских кварталов между двумя узлами (то есть abs(Ax - Bx) + abs(Ay - By)). Если бы мы могли двигаться по диагонали, то значение было бы равно sqrt( (Ax - Bx)^2 + (Ay - By)^2 ), и так далее. Самое важное то, что мы никогда не получаем слишком высокую оценку стоимости.
Итак, вот немагическая версия choose_node:
function choose_node (reachable):
min_cost = infinity
best_node = None
for node in reachable:
cost_start_to_node = node.cost
cost_node_to_goal = estimate_distance(node, goal_node)
total_cost = cost_start_to_node + cost_node_to_goal
if min_cost > total_cost:
min_cost = total_cost
best_node = node
return best_node
Функция, оценивающая расстояние от текущего до конечного узла, называется эвристикой, и этот алгоритм поиска, леди и джентльмены, называется … A*.
Интерактивное демо
Пока вы оправляетесь от шока, вызванного осознанием того, что загадочный A* на самом деле настолько прост, можете посмотреть на демо (или запустить его в оригинале статьи). Вы заметите, что в отличие от предыдущего примера, поиск тратит очень мало времени на движение в неверном направлении.

Заключение
Наконец-то мы дошли до алгоритма A*, который является не чем иным, как описанным в первой части статьи общим алгоритмом поиска с некоторыми усовершенствованиями, описанными во второй части, и использующим функцию choose_node, которая выбирает узел, который по нашей оценке приближает нас к конечному узлу. Вот и всё.
Вот вам для справки полный псевдокод основного метода:
function find_path (start_node, end_node):
reachable = [start_node]
explored = []
while reachable is not empty:
# Choose some node we know how to reach.
node = choose_node(reachable)
# If we just got to the goal node, build and return the path.
if node == goal_node:
return build_path(goal_node)
# Don't repeat ourselves.
reachable.remove(node)
explored.add(node)
# Where can we get from here that we haven't explored before?
new_reachable = get_adjacent_nodes(node) - explored
for adjacent in new_reachable:
# First time we see this node?
if adjacent not in reachable:
reachable.add(adjacent)
# If this is a new path, or a shorter path than what we have, keep it.
if node.cost + 1 < adjacent.cost:
adjacent.previous = node
adjacent.cost = node.cost + 1
# If we get here, no path was found :(
return None
Метод build_path:
function build_path (to_node):
path = []
while to_node != None:
path.add(to_node)
to_node = to_node.previous
return path
А вот метод choose_node, который превращает его в A*:
function choose_node (reachable):
min_cost = infinity
best_node = None
for node in reachable:
cost_start_to_node = node.cost
cost_node_to_goal = estimate_distance(node, goal_node)
total_cost = cost_start_to_node + cost_node_to_goal
if min_cost > total_cost:
min_cost = total_cost
best_node = node
return best_node
Вот и всё.
А зачем же нужна часть 4?
Теперь, когда вы поняли, как работает A*, я хочу рассказать о некоторых потрясающих областях его применения, которые далеко не ограничиваются поиском путей в сетке ячеек.
Часть 4. A* на практике
Первые три части статьи начинаются с самых основ алгоритмов поиска путей и заканчиваются чётким описанием алгоритма A*. Всё это здорово в теории, но понимание того, как это применимо на практике — совершенно другая тема.
Например, что будет, если наш мир не является сеткой?
Что если персонаж не может мгновенно поворачиваться на 90 градусов?
Как построить граф, если мир бесконечен?
Что если нас не волнует длина пути, но мы зависим от солнечной энергии и нам как можно больше нужно находиться под солнечным светом?
Как найти кратчайший путь к любому из двух конечных узлов?
Функция стоимости
В первых примерах мы искали кратчайший путь между начальным и конечным узлами. Однако вместо того, чтобы хранить частичные длины путей в переменной length, мы назвали её cost. Почему?
Мы можем заставить A* искать не только кратчайший, но и лучший путь, причём определение «лучшего» можно выбирать, исходя из наших целей. Когда нам нужен кратчайший путь, стоимостью является длина пути, но если мы хотим минимизировать, например, потребление топлива, то нужно использовать в качестве стоимости именно его. Если мы хотим по максимуму увеличить «время, проводимое под солнцем», то затраты — это время, проведённое без солнца. И так далее.
В общем случае это означает, что с каждым ребром графа связаны соответствующие затраты. В показанных выше примерах стоимость задавалась неявно и считалась всегда равной 1, потому что мы считали шаги на пути. Но мы можем изменить стоимость ребра в соответствии с тем, что мы хотим минимизировать.
Функция критерия
Допустим, наш объект — это автомобиль, и ему нужно добраться до заправки. Нас устроит любая заправка. Требуется кратчайший путь до ближайшей АЗС.
Наивный подход будет заключаться в вычислении кратчайшего пути до каждой заправки по очереди и выборе самого короткого. Это сработает, но будет довольно затратным процессом.
Что если бы мы могли заменить один goal_node на метод, который по заданному узлу может сообщить, является ли тот конечным или нет. Благодаря этому мы сможем искать несколько целей одновременно. Также нам нужно изменить эвристику, чтобы она возвращала минимальную оцениваемую стоимость всех возможных конечных узлов.
В зависимости от специфики ситуации мы можем и не иметь возможности достичь цели идеально, или это будет слишком много стоить (если мы отправляем персонажа через половину огромной карты, так ли важна разница в один дюйм?), поэтому метод is_goal_node может возвращать true, когда мы находимся «достаточно близко».
Полная определённость не обязательна
Представление мира в виде дискретной сетки может быть недостаточным для многих игр. Возьмём, например, шутер от первого лица или гоночную игру. Мир дискретен, но его нельзя представить в виде сетки.
Но есть проблема и посерьёзней: что если мир бесконечен? В таком случае, даже если мы сможем представить его в виде сетки, то у нас просто не будет возможности построить соответствующий сетке граф, потому что он должен быть бесконечным.
Однако не всё потеряно. Разумеется, для алгоритма поиска по графам нам определённо нужен граф. Но никто не говорил, что граф должен быть исчерпывающим!
Если внимательно посмотреть на алгоритм, то можно заметить, что мы ничего не делаем с графом, как целым; мы исследуем граф локально, получая узлы, которых можем достичь из рассматриваемого узла. Как видно из демо A*, некоторые узлы графа вообще не исследуются.
Так почему бы нам просто не строить граф в процессе исследования?
Мы делаем текущую позицию персонажа начальным узлом. При вызове get_adjacent_nodes она может определять возможные способы, которыми персонаж способен переместиться из данного узла, и создавать соседние узлы на лету.
За пределами трёх измерений
Даже ваш мир действительно является 2D-сеткой, нужно учитывать и другие аспекты. Например, что если персонаж не может мгновенно поворачиваться на 90 или 180 градусов, как это обычно и бывает?
Состояние, представляемое каждым узлом поиска, не обязательно должно быть только позицией; напротив, оно может включать в себя произвольно сложное множество значений. Например, если повороты на 90 градусов занимают столько же времени, сколько переход из одной ячейки в другую, то состояние персонажа может задаваться как [position, heading]. Каждый узел может представлять не только позицию персонажа, но и направление его взгляда; и новые рёбра графа (явные или косвенные) отражают это.
Если вернуться к исходной сетке 5×5, то начальной позицией поиска теперь может быть [A, East]. Соседними узлами теперь являются [B, East] и [A, South] — если мы хотим достичь F, то сначала нужно скорректировать направление, чтобы путь обрёл вид [A, East], [A, South], [F, South].
Шутер от первого лица? Как минимум четыре измерения: [X, Y, Z, Heading]. Возможно, даже [X, Y, Z, Heading, Health, Ammo].
Учтите, что чем сложнее состояние, тем более сложной должна быть эвристическая функция. Сам по себе A* прост; искусство часто возникает благодаря хорошей эвристике.
Заключение
Цель этой статьи — раз и навсегда развеять миф о том, что A* — это некий мистический, не поддающийся расшифровке алгоритм. Напротив, я показал, что в нём нет ничего загадочного, и на самом деле его можно довольно просто вывести, начав с самого нуля.
Дальнейшее чтение
У Амита Патела есть превосходное «Введение в алгоритм A*» [перевод на Хабре] (и другие его статьи на разные темы тоже великолепны!).
