[Перевод] Программирование — больше, чем кодинг

Это статья-перевод Стэнфордского семинара. Но перед ней небольшое вступление. Как образуются зомби? Каждый попадал в ситуацию, когда хочется подтянуть друга или коллегу до своего уровня, а не получается. Причём «не получается» не столько у тебя, сколько у него: на одной чаше весов находится нормальная зарплата, задачи и так далее, а на другой — необходимость думать. Думать неприятно и больно. Он быстро сдаётся и продолжает писать код, совершенно не включая мозг. Ты представляешь, насколько много сил нужно потратить, чтобы преодолеть барьер выученной беспомощности, и просто не делаешь этого. Так образуются зомби, которых вроде бы можно вылечить, но вроде бы и никто этим заниматься не станет.
Когда я увидел, что Лесли Лэмпорт (да-да, тот самый товарищ из учебников) приезжает в Россию и делает не доклад, а сессию вопросов-ответов, я немного насторожился. Вторым настораживающим фактором является его требование: каждый, кто придёт, должен (совершенно бесплатно) заранее прослушать пару его докладов, придумать по ним минимум один вопрос и только тогда уже приходить. Решил посмотреть, что там Лэмпорт вещает — и это великолепно! Это в точности та штука, волшебная ссылка-таблетка для лечения зомбятины. Одна из нескольких, причем рассказывает её товарищ, который действительно может себе позволить быть Д'Артаньяном во всём белом. Предупреждаю: от текста может знатно подгореть у любителей сверхгибких методологий и нелюбителей тестировать написанное. Знаю, что многие не любят Ютуб и то, сколько времени он тратит на просмотр докладов, поэтому под катом будет полная текстовая расшифровка в виде статьи.
Итак, программирование — больше, чем написание кода…
За какое бы задание вы ни взялись, вам всегда нужно пройти три шага:
- определиться, какой цели вы хотите достичь;
- решить, как именно вы будете добиваться своей цели;
- прийти к своей цели.
Это касается и программирования. Когда мы пишем код, нам необходимо:
- решить, что именно должна делать программа;
- определить, как именно она должна выполнять свою задачу;
- написать соответствующий код.
Последний шаг, конечно, очень важен, но о нем я говорить сегодня не буду. Вместо этого мы обсудим первые два. Их выполняет каждый программист прежде, чем начать работать. Вы не садитесь писать, если не решили, что именно пишете: браузер или базу данных. Определенное представление о цели обязательно должно присутствовать. И вы обязательно продумываете, что именно программа будет делать, а не пишете кое-как в надежде, что код сам как-нибудь превратится в браузер.
Как именно происходит это предварительное продумывание кода? Сколько усилий нам следует на это тратить? Все зависит от того, насколько сложную проблему мы решаем. Предположим, мы хотим написать отказоустойчивую распределенную систему. В этом случае нам следует обдумать все как следует, прежде чем садиться за код. А если нам просто нужно увеличить целочисленную переменную на 1? На первый взгляд, здесь все тривиально, и никаких размышлений не нужно, но потом мы вспоминаем, что может произойти переполнение. Поэтому, даже для того, чтобы понять, простая проблема или сложная — вначале нужно подумать.
Если предварительно продумать возможные решения проблемы, можно избежать ошибок. Но для этого нужно, чтобы ваше мышление было ясным. Чтобы этого добиться, нужно записывать свои мысли. Мне очень нравится цитата Дика Гиндона: «Когда вы пишете, природа демонстрирует вам, насколько неряшливо ваше мышление». Если вы не пишете, вам только кажется, что вы мыслите. А записывать свои мысли нужно в форме спецификаций.
Спецификации выполняют множество функций, в особенности в крупных проектах. Но я буду говорить только об одной из них: они помогают нам ясно мыслить. Ясно мыслить очень важно и довольно трудно, поэтому здесь нам нужно любое подспорье. На каком языке нам следует писать спецификации? Это вообще всегда первый вопрос для программистов: на каком языке мы будем писать. Одного правильного ответа на него нет: проблемы, которые мы решаем, слишком многообразные. Для некоторых полезен TLA+ — это язык спецификаций, который я разработал. Для других удобнее пользоваться китайским. Все зависит от ситуации.
Более важен другой вопрос: как добиться более ясного мышления? Ответ: мы должны мыслить как ученые. Это способ мышления, который отлично зарекомендовал себя за последние 500 лет. В науке мы строим математические модели реальности. Астрономия была, пожалуй, первой наукой в строгом смысле этого слова. В математической модели, используемой в астрономии, небесные тела предстают как точки с массой, положением и импульсом, хотя в реальности они являются крайне сложными объектами с горами и океанами, приливами и отливами. Эта модель, как и любая другая, создана для решения определенных задач. Она отлично подходит для того, чтобы определить, куда нужно направить телескоп, если нужно найти планету. Но если вы хотите предсказать погоду на этой планете, эта модель не подойдет.
Математика позволяет нам определить свойства модели. А наука показывает, как эти свойства соотносятся с реальностью. Поговорим о нашей науке, computer science. Реальность, с которой мы работаем — это вычислительные системы самых разных видов: процессоры, игровые консоли, компьютеры, выполняющие программы и так далее. Я буду говорить о выполнении программы на компьютере, но, по большому счету, все эти выводы применимы к любой вычислительной системе. В нашей науке мы используем множество различных моделей: машина Тьюринга, частично упорядоченные множества событий и многие другие.
Что такое программа? Это любой код, который можно рассматривать самостоятельно. Предположим, нам нужно написать браузер. Мы выполняем три задачи: проектируем представление программы для пользователя, затем пишем высокоуровневую схему программы, и, наконец, пишем код. По ходу написания кода мы понимаем, что нам нужно написать средство для форматирования текста. Здесь нам опять нужно решить три задачи: определить, какой текст это средство будет возвращать; выбрать алгоритм для форматирования; написать код. У этой задачи своя подзадача: правильно вставлять дефис в слова. Эту подзадачу мы тоже решаем в три шага — как видим, они повторяются на многих уровнях.
Рассмотрим более подробно первый шаг: какую задачу решает программа. Здесь мы чаще всего моделируем программу как функцию, которая получает некоторые входные данные и дает некоторые данные на выходе. В математике функция обычно описывается как упорядоченное множество пар. Например, функция возведения в квадрат для натуральных чисел описывается как множество {<0,0>, <1,1>, <2,4>, <3,9>, …}. Область определения такой функции — множество первых элементов каждой пары, то есть натуральные числа. Чтобы определить функцию, нам нужно указать ее область определения и формулу.
Но функции в математике — это не то же, что функции в языках программирования. Математика значительно проще. Поскольку на сложные примеры у меня времени нет, рассмотрим простой: функция в языке С или статический метод в Java, возвращающий наибольший общий делитель двух целых чисел. В спецификации этого метода мы напишем: вычисляет GCD(M,N) для аргументов M и N, где GCD(M,N) — функция, область определения которой — множество пар целых чисел, а возвращаемое значение — наибольшее целое число, на которое делится M и N. Как с этой моделью соотносится реальность? Модель оперирует с целыми числами, а в C или Java мы имеем 32-битный int. Эта модель позволяет нам решить, правилен ли алгоритм GCD, но она не предотвратит ошибки переполнения. Для этого потребовалась бы более сложная модель, на которую нет времени.
Поговорим об ограничениях функции как модели. Работа некоторых программ (например, операционных систем) не сводится к тому, чтобы вернуть определенное значение для определенных аргументов, они могут выполняться непрерывно. Кроме того, функция как модель плохо подходит для второго шага: планирования способа решения задачи. Быстрая сортировка и сортировка пузырьком вычисляют одну и ту же функцию, но это совершенно разные алгоритмы. Поэтому для описания способа достижения цели программы я использую другую модель, назовем ее стандартная поведенческая модель. Программа в ней представлена как множество всех допустимых поведений, каждое из которых, в свою очередь, является последовательностью состояний, а состояние — это присвоение значений переменным.
Давайте посмотрим, как будет выглядеть второй шаг для алгоритма Евклида. Нам нужно вычислить GCD(M, N). Мы инициализируем M как x, а N как y, затем повторно отнимаем меньшую из этих переменных от большей до тех пор, пока они не будут равны. Например, если M = 12, а N = 18, мы можем описать следующее поведение:
[x = 12, y = 18] → [x = 12, y = 6] → [x = 6, y = 6]
А если M = 0 и N = 0? Ноль делится на все числа, поэтому наибольшего делителя в этом случае нет. В этой ситуации нам нужно вернуться к первому шагу и спросить: действительно ли нам нужно вычислять НОД для неположительных чисел? Если в этом нет необходимости, то нужно просто изменить спецификацию.
Здесь следует сделать небольшое отступление о продуктивности. Её часто измеряют в количестве строк кода, написанных за день. Но ваш труд значительно полезнее, если вы избавились от определенного количества строк, потому что у вас стало меньше места для багов. И избавляться от кода проще всего именно на первом шаге. Вполне возможно, что вам просто не нужны все те навороты, которые вы пытаетесь реализовать. Самый быстрый способ упростить программу и сэкономить время — не делать вещи, которые не стоит делать. Второй шаг — на втором месте по потенциалу для экономии времени. Если вы измеряете продуктивность в количестве написанных строк, то продумывание способа выполнения задачи сделает вас менее продуктивными, поскольку вы сможете решить ту же задачу меньшим объемом кода. Точную статистику я здесь привести не могу, поскольку у меня нет способа посчитать то количество строк, которые я не написал благодаря тому, что потратил время на спецификацию, то есть на первый и второй шаги. И эксперимент тут тоже не поставить, потому что в эксперименте мы не имеем права выполнить первый шаг, задание определено заранее.
В неформальных спецификациях легко не учесть многие трудности. Ничего сложного в написании строгих спецификаций для функций нет, обсуждать это я не буду. Вместо этого мы поговорим о написании строгих спецификаций для стандартных поведенческих моделей. Есть теорема, которая гласит, что любое множество поведений можно описать с помощью свойства безопасности (safety) и свойства живучести (liveness). Безопасность означает, что ничего плохого не произойдет, программа не выдаст неверный ответ. Живучесть означает, что рано или поздно произойдет что-то хорошее, т. е. программа рано или поздно даст правильный ответ. Как правило, безопасность является более важным показателем, ошибки чаще всего возникают именно здесь. Поэтому для экономии времени я не буду говорить об живучести, хотя она, конечно, тоже важна.
Мы добиваемся безопасности, прописывая, во-первых, множество возможных исходных состояний. И, во-вторых, отношения со всеми возможными следующими состояниями для каждого состояния. Будем вести себя как ученые и определим состояния математически. Набор исходных состояний описывается формулой, например, в случае алгоритма Евклида: (x = M) ∧ (y = N). Для определенных значений M и N существует только одно исходное состояние. Отношение со следующим состоянием описывается формулой, в которой переменные следующего состояния записываются со штрихом, а текущего состояния — без штриха. В случае с алгоритмом Евклида мы будем иметь дело с дизъюнкцией двух формул, в одной из которых x является наибольшим значением, а во второй — y:
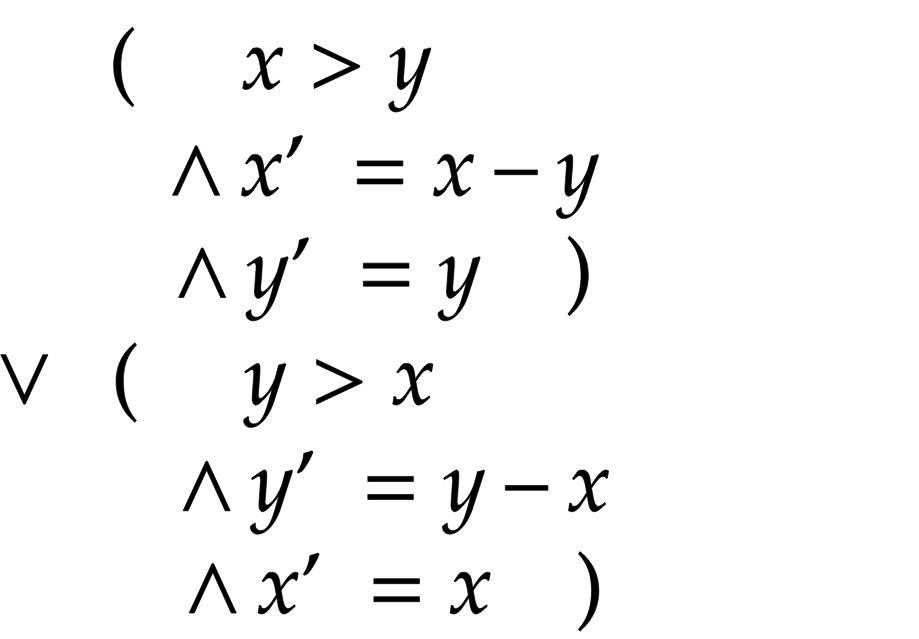
В первом случае новое значение y равно прежнему значению y, а новое значение x мы получаем, отняв от большей переменной меньшую. Во втором случае мы делаем наоборот.
Вернемся к алгоритму Евклида. Предположим вновь, что M = 12, N = 18. Это определяет единственное исходное состояние, (x = 12) ∧ (y = 18). Затем мы подставляем эти значения в формулу выше и получаем:

Здесь единственное возможное решение: x' = 18 - 12 ∧ y' = 12, и мы получаем поведение: [x = 12, y = 18]. Точно так же мы можем описать все состояния в нашем поведении: [x = 12, y = 18] → [x = 12, y = 6] → [x = 6, y = 6].
В последнем состоянии [x = 6, y = 6] обе части выражения будут ложны, следовательно, следующего состояния у него нет. Итак, мы имеем полную спецификацию второго шага — как видим, это вполне обычная математика, как у инженеров и ученых, а не странная, как в computer science.
Эти две формулы можно объединить в одну формулу темпоральной логики. Она элегантна и объяснить ее нетрудно, но на неё сейчас нет времени. Темпоральная логика нам может понадобиться только для свойства живости, для безопасности она не нужна. Темпоральная логика как таковая не нравится, это не вполне обычная математика, но в случае с живостью она является необходимым злом.
В алгоритме Евклида для каждого значения x и y есть уникальные значения x' и y', которые делают отношение со следующим состоянием истинным. Другими словами, алгоритм Евклида детерминированный. Чтобы смоделировать недетерминированный алгоритм, нужно, чтобы у текущего состояния было несколько возможных будущих состояний, и чтобы у каждого значения переменной без штриха было несколько значений переменной со штрихом, при которых отношение со следующим состоянием является истинным. Это несложно сделать, но сейчас приводить примеры я не буду.
Чтобы сделать работающий инструмент, нужна формальная математика. Как сделать спецификацию формальной? Для этого нам понадобится формальный язык, например, TLA+. Спецификация алгоритма Евклида будет на этом языке выглядеть следующим образом:

Символ знака равенства с треугольником означает, что значение слева от знака определено как равное значению справа от знака. В сущности, спецификация — это определение, в нашем случае два определения. К спецификации в TLA+ нужно добавить объявления и некоторый синтаксис, как на слайде выше. В ASCII это будет выглядеть так:

Как видим, ничего сложного. Спецификацию на TLA+ можно проверить, т. е. обойти все возможные поведения в небольшой модели. В нашем случае этой моделью будут определенные значения M и N. Это очень эффективный и простой способ проверки, который целиком выполняется автоматически. Кроме того, можно написать формальные доказательства истинности и проверить их механически, но для этого нужно много времени, поэтому так почти никто не делает.
Главный недостаток TLA+ в том, что это математика, а программисты и computer scientists боятся математики. На первый взгляд это звучит как шутка, но, к сожалению, я говорю это на полном серьезе. Мой коллега только что рассказывал мне, как он пытался объяснить TLA+ нескольким разработчикам. Как только на экране появились формулы, у них сразу же сделались стеклянные глаза. Так что если TLA+ пугает, можно использовать PlusCal, это своего рода игрушечный язык программирования. Выражение в PlusCal может быть любым выражением TLA+, то есть, по большому счету, любым математическим выражением. Кроме того, в PlusCal есть синтаксис для недетерминистичных алгоритмов. Благодаря тому, что в PlusCal можно записать любое выражение TLA+, он является значительно более выразительным любого реального языка программирования. Далее, PlusCal компилируется в легко читаемую спецификацию TLA+. Это не значит, конечно, что сложная спецификация PlusCal превратится в простую на TLA+ — просто соответствие между ними очевидное, не появится дополнительной сложности. Наконец, эту спецификацию можно будет проверить инструментами TLA+. В общем, PlusCal может помочь преодолеть фобию математики, его легко понять даже программистам и computer scientists. В прошлом я какое-то время (около 10 лет) публиковал на нем алгоритмы.
Возможно, кто-то возразит, что TLA+ и PlusCal — это математика, а математика работает только на придуманных примерах. На практике же нужен реальный язык с типами, процедурами, объектами и так далее. Это не так. Вот, что пишет Крис Ньюкомб, работавший в Amazon: «Мы использовали TLA+ в десяти крупных проектах, и в каждом случае его использование вносило значительный вклад в разработку, потому что мы смогли отловить опасные баги до попадания в продакшн, и потому что он дал нам понимание и уверенность, необходимые для агрессивных оптимизаций производительности, не влияющих на истинность программы». Часто можно услышать, что при использовании формальных методов мы получаем неэффективный код — на практике же все ровно наоборот. Кроме того, бытует мнение, что менеджеров невозможно убедить в необходимости формальных методов, даже если программисты убеждены в их полезности. А Ньюкомб пишет: «Менеджеры теперь всячески подталкивают к тому, чтобы писать спецификации на TLA+, и специально выделяют на это время». Так что когда менеджеры видят, что TLA+ работает, они с радостью его принимают. Крис Ньюкомб написал это где-то шесть месяцев тому назад (в октябре 2014 года), сейчас же, насколько я знаю, TLA+ используется в 14 проектах, а не 10. Другой пример относится к проектированию XBox 360. К Чарльзу Текеру пришел стажер и написал спецификацию для системы памяти. Благодаря этой спецификации был найден баг, который иначе был бы не замечен, и из-за которого каждая XBox 360 падала бы после четырех часов использования. Инженеры из IBM подтвердили, что их тесты не обнаружили бы этот баг.
Более подробно про TLA+ вы можете почитать в интернете, а сейчас давайте поговорим о неформальных спецификациях. Нам редко приходится писать программы, которые вычисляют наименьший общий делитель и тому подобное. Значительно чаще мы пишем программы вроде инструмента структурной распечатки (pretty-printer), который я написал для TLA+. После самой простой обработки код на TLA+ выглядел бы следующим образом:

Но в приведенном примере пользователь скорее всего хотел, чтобы знаки конъюнкции и равенства были выравнены. Так что правильное форматирование выглядело бы скорее так:
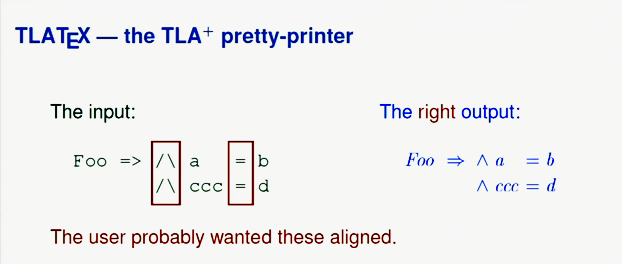
Рассмотрим другой пример:

Здесь, наоборот, выравнивание знаков равенства, сложения и умножения в источнике было случайным, поэтому самой простой обработки вполне достаточно. В общем, точного математического определения верного форматирования нет, потому что «правильное» в данном случае значит «такое, какое хочет пользователь», а это математически определить нельзя.
Казалось бы, если у нас нет определения истинности, то спецификация бесполезна. Но это не так. Если мы не знаем, что именно программа должна сделать, это не значит, что нам не нужно продумывать ее работу — наоборот, мы должны потратить на это еще больше усилий. Спецификация здесь особенно важна. Определить оптимальную программу для структурной распечатки невозможно, но это не значит, что мы не должны за нее браться вообще, а писать код как поток сознания — это не дело. В итоге я написал спецификацию из шести правил с определениями в форме комментариев в Java-файле. Вот пример одного из правил: a left-comment token is LeftComment aligned with its covering token. Это правило написано на, скажем так, математическом английском: LeftComment aligned, left-comment и covering token — термины с определениями. Это то, как математики описывают математику: пишут определения терминов и на основе них — правила. Польза от такой спецификации в том, что понять и отладить шесть правил значительно проще, чем 850 строк кода. Надо сказать, что написать эти правила было непросто, довольно много времени ушло на их отладку. Специально для этой цели я написал код, который сообщал, какое именно правило используется. Благодаря тому, что я проверил эти шесть правил на нескольких примерах, мне не нужно было отлаживать 850 строк кода, и баги оказалось довольно легко найти. В Java для этого есть отличные инструменты. Если бы я просто написал код, то у меня ушло бы значительно больше времени, и форматирование получилось бы худшего качества.
Почему нельзя было использовать формальную спецификацию? С одной стороны, правильность выполнения здесь не слишком важна. Структурная распечатка обязательно кому-то не угодит, так что мне не нужно было добиваться правильной работы во всех неординарных ситуациях. Еще важнее тот факт, что у меня не было адекватных инструментов. Средство для проверки моделей TLA+ здесь бесполезно, так что мне пришлось бы вручную писать примеры.
У приведенной спецификации есть черты, общие для всех спецификаций. Она более высокого уровня, чем код. Реализовать ее можно на любом языке. Для ее написания бесполезны какие-либо инструменты или методы. Никакой курс программирования вам не поможет написать эту спецификацию. И не существует инструментов, которые могли бы сделать эту спецификацию ненужной, если, конечно, вы не пишете язык специально для написания программ структурной распечатки на TLA+. Наконец, эта спецификация ничего не говорит о том, как именно мы будем писать код, в ней только указывается, что этот код делает. Мы пишем спецификацию, чтобы помочь нам продумать проблему, прежде чем мы начнем думать о коде.
Но у этой спецификации есть и особенности, отличающие ее от других спецификаций. 95% других спецификаций значительно короче и проще:

Далее, эта спецификация является набором правил. Как правило, это признак плохой спецификации. Понять последствия набора правил довольно трудно, и именно поэтому мне пришлось потратить много времени на их отладку. Тем не менее, в данном случае лучшего способа мне было не найти.
Стоит сказать несколько слов о программах, которые работают непрерывно. Как правило, они работают параллельно, например, операционные системы или распределенные системы. Разобраться в них в уме или на бумаге могут очень немногие, и я к их числу не принадлежу, хотя когда-то мне это было по силам. Поэтому необходимы инструменты, которые будут проверять нашу работу — например, TLA+ или PlusCal.
Зачем нужно было писать спецификацию, если я и так знал, что именно код должен делать? На самом деле, мне только казалось, будто бы я это знаю. Кроме того, при наличии спецификации постороннему человеку уже не нужно залезать в код, чтобы понять, что именно он делает. У меня есть правило: не должно быть никаких общих правил. У этого правила, конечно же, есть исключение, это единственное общее правило, которому я следую: спецификация того, что делает код, должна сообщать людям все, что им нужно знать при использовании этого кода.
Итак, что именно программистам нужно знать о мышлении? Для начала, то же, что и всем: если ты не пишешь, то тебе только кажется, что ты мыслишь. Кроме того, нужно думать, прежде чем кодить, а это значит, нужно писать, прежде чем кодить. Спецификация — это то, что мы пишем перед тем, как начать кодить. Спецификация нужна для любого кода, который может быть кем-либо использован или изменен. И этим «кто-либо» может оказаться сам автор кода через месяц после его написания. Спецификация нужна для больших программ и систем, для классов, для методов и иногда даже для сложных участков отдельного метода. Что именно нужно писать о коде? Нужно описать, что он делает, то есть то, что может быть полезно любому человеку, использующему этот код. Иногда может также быть необходимо указать, как именно код достигает своей цели. Если этот способ мы проходили в курсе алгоритмов, то мы называем это алгоритмом. Если же это нечто более специальное и новое, то мы называем это высокоуровневым проектированием. Формальной разницы здесь нет: и то, и другое является абстрактной моделью программы.
Как именно следует писать спецификацию кода? Главное: она должна быть на уровень выше самого кода. Она должна описывать состояния и поведения. Она должна быть настолько строгой, насколько этого требует задача. Если вы пишете спецификацию способа реализации задачи, то ее можно написать на псевдокоде или при помощи PlusCal. Учиться писать спецификации нужно на формальных спецификациях. Это даст вам необходимые навыки, которые помогут в том числе и с неформальными. А как научиться писать формальные спецификации? Когда мы учились программированию, мы писали программы, а затем отлаживали их. То же самое здесь: нужно написать спецификацию, проверить ее при помощи средства проверки моделей и исправить ошибки. TLA+, возможно, не самый лучший язык для формальной спецификации, и для ваших конкретных нужд скорее всего лучше подойдет другой язык. Преимущество TLA+ в том, что он отлично учит математическому мышлению.
Как связать спецификацию и код? При помощи комментариев, которые связывают математические понятия и их реализацию. Если вы работаете с графами, то на уровне программы у вас будут массивы узлов и массивы связей. Поэтому вам нужно написать, как именно граф реализуется этими структурами программирования.
Нужно заметить, что ничто из вышесказанного не относится к самому процессу написания кода. Когда вы пишете код, то есть выполняете третий шаг, вам тоже нужно мыслить и продумывать программу. Если подзадача оказывается сложной или неочевидной, нужно написать для нее спецификацию. Но о самом коде я здесь не говорю. Вы можете пользоваться любым языком программирования, любой методологией, речь не о них. Кроме того, ничто из вышесказанного не избавляет от необходимости тестировать и отлаживать код. Даже если абстрактная модель написана верно, в ее реализации могут быть баги.
Написание спецификаций — дополнительный этап в процессе написания кода. Благодаря нему многие ошибки можно отловить меньшими усилиями — мы это знаем по опыту программистов из Amazon. Со спецификациями качество программ становится выше. Так почему же тогда мы так часто обходимся без них? Потому что писать трудно. А писать трудно, потому что для этого нужно думать, а думать тоже трудно. Всегда проще делать вид, что думаешь. Здесь можно провести аналогию с бегом — чем меньше вы бегаете, тем медленнее вы бежите. Нужно тренировать свои мускулы и упражняться в письме. Нужна практика.
Спецификация может быть неверной. Вы могли где-то сделать ошибку, или могли измениться требования, или оказалось необходимо сделать улучшение. Любой код, которым кто-либо пользуется, приходится менять, поэтому рано или поздно спецификация перестанет соответствовать программе. В идеале в этом случае нужно написать новую спецификацию и полностью переписать код. Мы прекрасно знаем, что так никто не делает. На практике мы патчим код и, возможно, обновляем спецификацию. Если это обязательно рано или поздно происходит, то зачем вообще писать спецификации? Во-первых, для человека, который будет править ваш код, каждое лишнее слово в спецификации будет на вес золота, и этим человеком вполне можете быть вы сами. Я часто ругаю себя за недостаточную спецификацию, когда правлю свой код. А я пишу больше спецификаций, чем кода. Поэтому, когда вы правите код, спецификацию всегда нужно обновлять. Во-вторых, с каждой правкой код становится хуже, его становится все труднее читать и поддерживать. Это нарастание энтропии. Но если вы не начинаете со спецификации, то каждая написанная строка будет правкой, и код с самого начала будет громоздким и трудночитаемым.
Как говорил Эйзенхауер, ни одна битва не была выиграна по плану, и ни одна битва не была выиграна без плана. А он знал кое-что о битвах. Существует мнение, что написание спецификаций — пустая трата времени. Иногда это действительно так, и задача настолько проста, что продумывать ее нечего. Но всегда нужно помнить, что, когда вам советуют не писать спецификаций, это значит, что вам советуют не думать. И об этом каждый раз следует подумать. Продумывание задачи не гарантирует, что вы не совершите ошибок. Как мы знаем, волшебной палочки никто не изобрел, и программирование — сложное занятие. Но если вы не продумываете задачу, вы гарантированно сделаете ошибки.
Подробнее про TLA+ и PlusCal можно почитать на специальном сайте, туда можно зайти с моей домашней страницы по ссылке. На этом у меня все, спасибо за внимание.
Напоминаю, что это перевод. Когда вы будете писать комментарии — помните, что автор их не прочитает. Если вам действительно хочется пообщаться с автором, то он будет на конференции Hydra 2019, которая пройдёт 11–12 июля 2019 года в Санкт-Петербурге. Билеты можно приобрести на официальном сайте.
