[Перевод] Проблемы эгоистов: дорожные пробки и парадокс Браеса

Строительство более широких дорог может ухудшить ситуацию с дорожным движением. Обычно этот контринтуитивный и контрпродуктивный результат объясняют следующим образом: чем больше дороги, тем более крупные торговые центры они привлекают, что в свою очередь привлекает больше автомобилей. Но это ещё не вся история. В 1960-х Дитрих Браес обнаружил теоретическую конфигурацию дорог, в которой строительство новой соединительной дороги может замедлить движение каждого, даже если количество машин остаётся постоянным. И наоборот, закрытие одной дороги в сети Браеса позволит всем добираться домой быстрее. Такое явление настолько странно, что заслуживает собственного определения — «Парадокс Браеса».
Несколько лет назад Джоел Коэн сказал мне, что парадокс Браеса может стать хорошей темой для моей колонки в «Computing Science». Я засомневался. Опубликовано уже немало обсуждений этого парадокса, в том числе потрясающие статьи самого Коэна, а также книга Тима Рафгардена (обзор которой я написал для American Scientist). Я не считал, что смогу добавить что-то новое к дискуссии.
Однако недавно я начал рассматривать задачу визуализации парадокса Браеса — представлении его таким образом, чтобы мы могли наблюдать отдельные автомобили, едущие через дорожную сеть, а не просто вычислять средние скорости и время в пути. Возможность поэкспериментировать с моделью — понажимать рычаги и кнопки, попробовать разные алгоритмы маршрутизации — может привести к более чёткому пониманию того, почему хорошо информированные и имеющие собственный интерес водители могут выбирать маршрут, который в результате тормозит всех.
Теперь у меня есть работающая модель чего-то, напоминающего парадокс Браеса, написанная на JavaScript. Рекомендую попробовать прокатиться по ней. Также есть сопровождающая её колонка «Computing Science» в American Scientist, которая выложена на веб-сайте журнала в HTML и PDF. Если вам интересен исходный код, то он есть на Github. Здесь я хочу немного рассказать о реализации модели и о том, чему она меня научила.
Адаптация математической модели Браеса к более механистической и визуальной среде оказалась слжонее, чем я ожидал. Исходная формулировка довольно абстрактна и не особо физична; она ближе к теории графов, чем к проектированию автотрасс. На представленны ниже схемах широкие синие дороги, помеченные как A и B, никогда не оказываются перегруженными; вне зависимости от пропускаемого ими трафика время движения по ним всегда равно одному часу. На узких красных дорогах a и b время перемещения равно нулю, когда они пусты, но движение увеличивается с повышением нагрузки; если все машины соберутся на одной красной дороге, время движения по ней тоже становится равным одному часу. Золотой маршрут X волшебным образом обеспечивает мгновенную транспортировку любому количеству автомобилей.
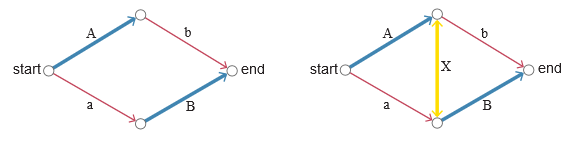
Наличие парадокса зависит от существования дороги X. Без золотого соединения (левая схема) трафик равномерно распределяется между маршрутами Ab и aB, и на всю поездку все автомобили тратят 90 минут. При открытии соединения X(правая схема) все водители предпочитают маршрут aXb, и все проводят на дороге полные два часа.
Необходимым предположением для этого парадокса является то, что все стремятся к эгоистичному построению маршрута, выбирая тот путь, который обеспечивает самое быстрое перемещение, и игнорируя все другие факторы, кроме времени движения. Иронично то, что, упорствуя в том, чтобы ни у кого другого не было бы поездки короче, водители создают плотную пробку на маршруте aXb, в то время как AXB остаётся пустым. Почему? Если какой-нибудь водитель решит переместиться на AXB, то его отсутствие незначительно снизит нагрузку на aXb, что даст этому маршруту незначительное преимущество в скорости. Следуя эгоистичным устремлениям, сместившийся на другой путь водитель должен вернуться на aXb. Получается патовая ситуация.
Машины, двигающиеся с бесконечной скоростью, и дороги с бесконечной пропускной способностью вполне уместны в математической модели, но вызывают проблемы в симуляции, которая должна имитировать настоящее движение по шоссе. В поисках более реалистичной модели я пришёл к показанному ниже расположению дорог, вдохновлённому схемой из статьи Клода М. Пинчина 1997 года (Braess Paradox: maximum penalty in a minimal critical network. Transportation Research A 31(5):379–388).

Топология схемы та же, что и в исходной сети Браеса, но отличается геометрия, а значит и связь между переполнением и скоростью тоже. Цель по-прежнему заключается в том, чтобы добраться от начала до конца или от Origin до Destination. Отрезки дороги A и B по-прежнему широки и не подвержены дорожным пробкам. Дороги a и b более прямые и короткие, но в то же время более узкие. При нулевом трафике скорость машины на a и b такая же, как на A и B, но с увеличением нагрузки скорость падает. Аналогом «золотой дороги» является короткий мост в центре карты, обладающий теми же свойствами скорости, что и A с B. В исходной конфигурации мост заблокирован, но его можно открыть нажатием мыши. На показанном выше скриншоте работающей модели мост открыт и по нему идёт движение.
Автомобили, представленные цветными точками, входят в систему в пункте Origin. В момент входа каждая машина выбирает один из возможных маршрутов. Если мост закрыт, есть всего два варианта: Ab и aB. Когда мост открыт, водители также могут выбрать короткую дорогу ab или более длинную AB. Затем машины движутся по выбранным маршрутам, подчиняясь ограничениям скорости на каждом отрезке, пока не достигают пункта Destination.
Эта схема в некоторых важных аспектах отличается от исходной формулировки Браеса. Демонстрирует ли она парадокс? Другими словами, увеличивается ли время движения, когда мост открыт и водители могут двигаться по маршрутам ab и AB? Ответом для широкого интервала значений параметров будет «да», и это видно из следующих результатов:
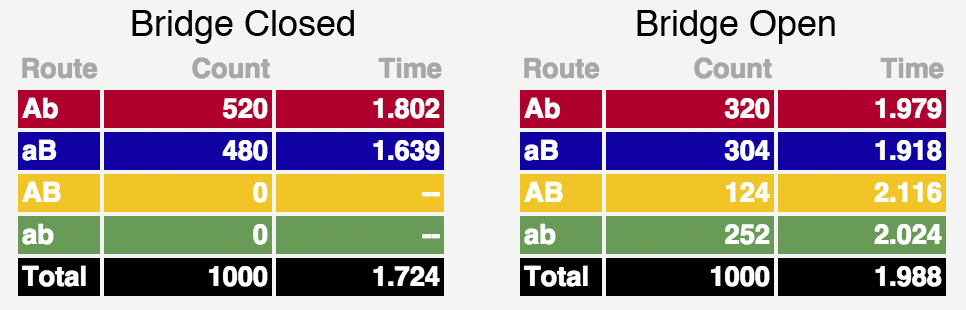
В таблицах показано количество машин, выбравших каждый из маршрутов и среднее время, потраченное ими на дорогу. (Время измерено в единицах самой быстрой из возможных поездок: по кратчайшему пути ab с нулевым трафиком.) Заметьте, что открытие моста замедлило скорость на всех четырёх маршрутах. Даже несмотря на то, что по маршрутам Ab и aB проходило на 37% меньше трафика, машинам на этих маршрутах требовалось на 9–15% больше времени для завершения поездки. Маршруты ab и AB были ещё медленнее.
Но числа не раскрывают ситуацию полностью — это было первое, что я понял после запуска симуляции. В случае с закрытым мостом, когда общий трафик разделяется на два приблизительно равных потока, можно предположить, что новые машины попеременно выбирают Ab или aB, так что, система достигает статистически равновесного состояния с равным количеством автомобилей на каждом из двух маршрутов в любой момент времени. Но происходит совершенно другое! Лучше всего убедиться в этом, запустив симуляцию, но и представленный ниже график тоже даёт нам общее понимание модели.
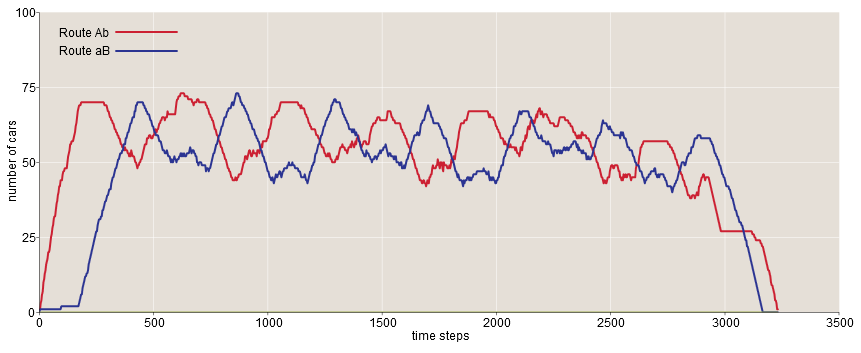
Вместо перехода в равновесное состояние система колеблется с периодом примерно в 500 временных отрезков, что примерно равно половине времени, которое требуется среднему автомобилю для перемещения из Origin в Destination. Две кривые сдвинуты по фазе почти ровно на 180 градусов.
Несложно понять, откуда появляются такие колебания. Когда каждый автомобиль попадает в дорожную сеть, он выбирает маршрут с кратчайшим ожидаемым временем поездки на основании состояния в текущий момент. Основным решающим фактором ожидаемого времени поездки является количество машин, занимающих отрезки a и b, на которых скорость уменьшается при заполнении дорог. Но когда машины выбирают менее популярный маршрут, они также повышают занятость этого маршрута, что делает его менее желательным для следующих за ними автомобилей. Кроме того, на маршруте Ab существует значительная задержка перед тем, как машины достигают отрезка, на который влияет переполнение. Задержка и асимметрия сети создаёт неустойчивость — контур обратной связи, в котором неизбежны выбросы и избыточная коррекция.
Когда соединительный мост открыт, паттерн становится более сложным, но колебания по-прежнему очень заметны:
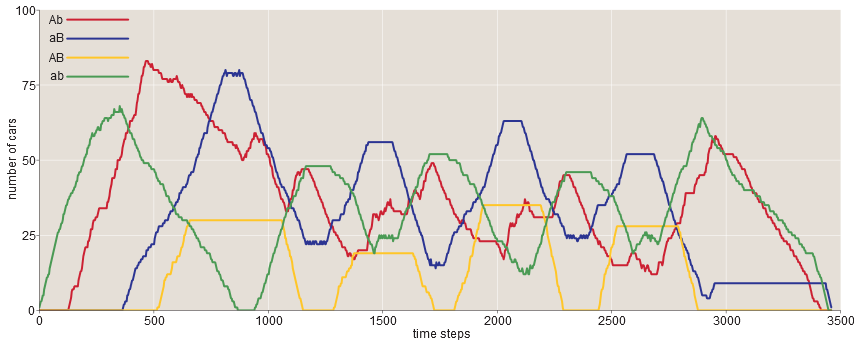
Похоже, что существуют две перемежающиеся фазы — в одной доминируют Ab и ab (в этой цветовой схеме — красно-зелёная рождественская фаза), в другой побеждают ab и AB (жёлто-зелёная «бойскаутская» фаза). Период волн менее регулярен, но в основном он длиннее.
Я не первый наблюдаю такие колебания; например, они упоминаются Даниелем Бушемой и коллегами в статье, описывающей симуляцию похожих на браесовские дорожных сетей в NetLogo. Однако в целом таким колебаниям и неустойчивостям уделяют мало внимания в литературе.
Асимметрия схемы очень важна для создания и колебаний, и парадоксального замедления при открытии центрального соединительного узла. Вы можете убедиться в этом самостоятельно, запустив симметричную версию модели. Она оказывается довольно скучной.
Заслуживает комментария ещё один баг/фича динамической модели. В исходной сети Браеса соединения A и B имеют неограниченную вместимость; фактически, модель обещает, что время прохождения этих дорог будет постоянной, вне зависимости от трафика. В динамической модели с дискретными машинами с ненулевыми размерами это обещание сложно сдержать. Допустим, машины следуют по маршруту Ab и отрезок b совершенно забит. В точке соединения, где A переходит в b, машинам некуда деться, так что они возвращаются обратно в отрезок A, который из-за этого не может гарантировать постоянную скорость.
При реализации динамической модели я обнаружил, что существует множество вариантов решений, в выборе которых мне мало поможет математическая формулировка исходной системы Браеса. Одним из них стала проблема «обратного проникания очереди». Позволить ли машинам скапливаться на дороге или дать им невидимые буферы, в которых они могут спокойно ждать своей очереди, чтобы продолжить путешествие? А как насчёт машин, появляющихся в узле начала, когда для них нет места на дорогах? Нужно ли ставить их в очередь, отбрасывать их, позволять ли им блокировать машины, направляющиеся по другой дороге? Ещё один скользкий момент касается приоритетов и честности. Два узла рядом с серединой дорожной схемы имеют два входа и два выхода. Если в обеих очередях на входе стоят машины, ожидая прохода через узел, то какая двинется первой? Если не отнестись внимательно к выбору стратегии обработки таких пробок, то один маршрут будет постоянно заблокирован другим.
Изучив код на JavaScript, вы можете понять, какие решения выбрал я. Не буду утверждать, что мои ответы совершенно правильны. Но более важно то, что после множества экпериментво и исследований альтернативных решений я выяснил, что большинство подробностей не так уж и важно. Эффект Браеса оказывается достаточно стабильным, он проявляется во многих версиях модели с немного отличающимися предположениями и алгоритмами. Такая стабильность подсказывает нам, что стоит более внимательно искать на настоящих трассах свидетельства парадоксальных паттернов трафика.
