[Перевод] Приключения в математическом лесу фрактальных деревьев
Перевод поста Bernat Espigulé Pons, «Adventures into the Mathematical Forest of Fractal Trees».Скачать перевод в виде документа Mathematica, который содержит весь код использованный в статье, можно здесь.
Без сомнения, золотое сечение и в наше время представляется одним из самых таинственных, волшебных и поразительных чисел, которые известны людям: 
. (в языке Wolfram Language и системе Mathematica ему соответствует символ GoldenRatio). Как вы увидите из этого поста, это число действительно имеет множество интересных свойств, которые можно исследовать, причём некоторые из них рассматривались ещё в работах учёных Древней Греции, таких как Пифагор и Евклид, другие в работах итальянского математика Леонардо Пизанского, более известного под прозвищем Фибоначчи, или Иоганном Кеплером — астрономом эпохи Возрождения. Хотя это может прозвучать странно, в этом посте я расскажу вам о новых геометрических объектах, связанных с золотым сечением, которые осветили мне путь, когда я пытался отобразить неизвестную ранее область Математического Леса.Обнаруженные ниже свойства были найдены не как-то случайно, я упорно работал, чтобы добыть эти новые знания еще со времён, когда я учился в старшей школе. После того, как в 2007 году я увидел рисунки «золотых» (в плане использования при их построении золотого сечения) фрактальных деревьев Ганса Вальзера (Hans Walser), я понял, что в этой области ещё есть место новым исследованиям и открытиям. После некоторых поисков я нашел требующиеся мне для этого инструменты: ими стали система Mathematica и интерактивная модель Тео Грея под названием «Сгибатель обнажённого обдуваемого ветром дерева Пифагора», с сайта Wolfram Demonstrations Project. Собрав некоторые знания и начальные умения программирования на языке Wolfram Language, я получил свои первые результаты и озарения. Скажем, ниже вы можете видеть пример одного из первых самокасающихся «золотых» фрактальных деревьев, которые я открыл для себя, создав свою собственную версию «Сгибателя» Тео Грея, которую я изначально разрабатывал для изучения тернарных деревьев (т. е. деревьев, у которых из каждого узла выходит три ветви).
In[1]:=
Out[3]=
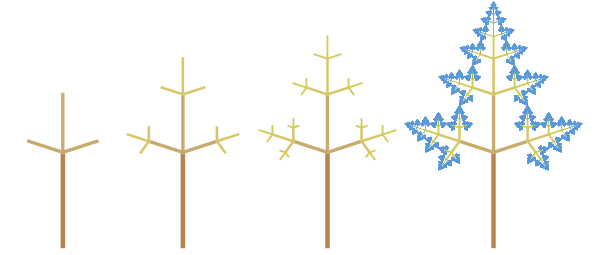
Это самоподобное дерево, т. е. дерево, которое получается, по сути, последовательным применением некоторого правила ветвления. Я называю «золотыми» те деревья, длина ветвей которых кратна золотому сечению GoldenRatio = φ. Для этого конкретного дерева, масштабный коэффициент для центральной ветви равен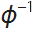 
, а для боковых ветвей 
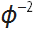. Угол между центральной ветвью и каждой из боковых ветвей равен 72º. Так как это дерево не имеет пересекающихся между собой ветвей или же не соединённых между собой элементов, то его можно называть «самокасающимся» деревом. Давайте взглянем на некоторые из его свойств поближе:
In[4]:=
Out[7]=
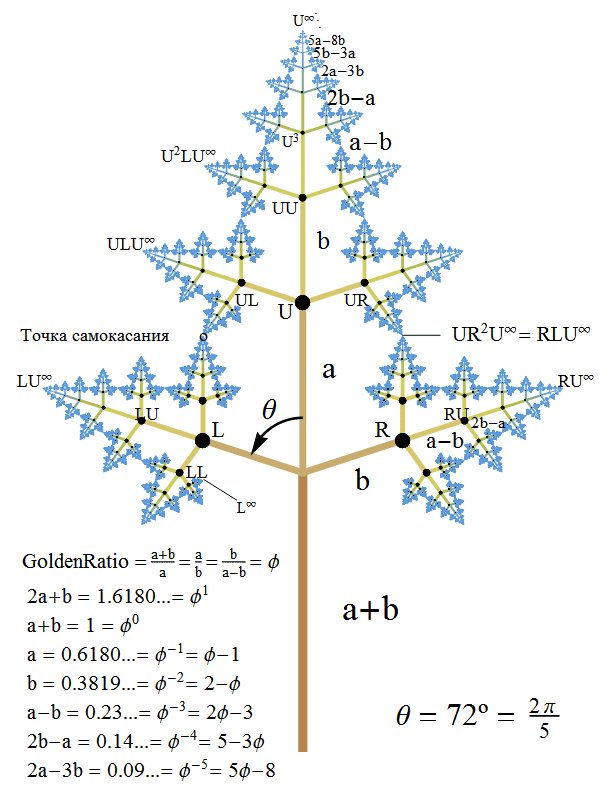
Вслед за обозначениями, предложенными Бенуа Мандельбротом (Benoit Mandelbrot) и Майклом Фрэймом (Michael Frame) для бинарных деревьев, я добавил третью букву U, вместе с которой мы сможем описать все ветви нашего тройного дерева. Буквой L обозначаются ветви, выходящие слева, буквой R — ветви, выходящие справа, а буква U соответствует центральной ветви. Таким образом, строка из этих букв однозначно задаёт каждую ветвь нашего фрактала. В том случае, если такого рода «адрес» имеет бесконечную длину, то мы можем указать конкретную «вершину» нашего фрактального дерева, которую можно рассматривать, по сути, как недостижимую предельную точку, к которой постепенно приближается цепочка ветвей фрактального дерева. Например, бесконечный «адрес» вида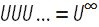 
задаёт «кончик» в самом верху нашего дерева:
In[8]:=
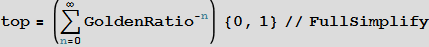
Out[8]=
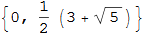
Таким образом, высота нашего дерева равна:
In[9]:=
Out[9]=
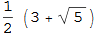
А его ширина равна расстоянию между точками 
и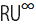 
:
In[10]:=
Out[10]=
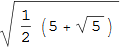
Также весьма интересно, что длина последовательности ветвей дерева может быть выражена с помощью чисел Фибоначчи (в Mathematica для поиска n-го по счёту числа Фибоначчи служит функция Fibonacci[n]). Вы можете найти некоторые выражения, используемые в коде ниже, в нижнем левом углу предыдущего рисунка:
In[11]:=
Out[11]=
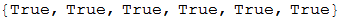
In[12]:=
Out[12]=
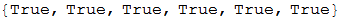
Наконец, для того, чтобы доказать, что это дерево является самокасающимся, нам необходимо показать, что две различные ветви (их вершины) касаются друг друга в одной точке, которая соответствует одновременно двум точкам (вершинам) дерева: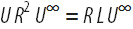 
. При этом тоже самое наблюдается и для зеркально симметричной точки (см. диаграмму ниже). Если это так, то самоподобие дерева будет означать, что в нём отсутствуют вершины, которые не касаются других вершин. Это означает, что можно взять любую вершину, «отрезать» подмножество дерева, содержащее её, которое повторяет по внешнему виду всё дерево, затем изменить соответствующим образом его масштаб, повернуть на нужный угол и мы получим после этого точку касания одного из двух рассмотренных основных типов:
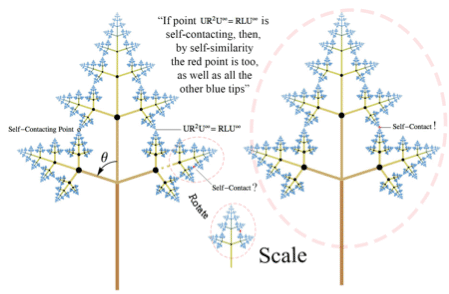Координаты вершины 
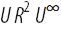можно определить следующим образом:
In[13]:=
Out[13]=
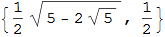
При этом координаты вершины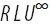 
будут равны:
In[14]:=
Out[14]=
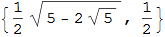
Таким образом, ввиду того, что эти координаты равны, мы можем утверждать, что наше дерево действительно является самокасающимся.
Еще одна потрясающая вещь, связанная с этим «золотым» деревом, заключается в том, что оно создаёт красивый узор с осевой симметрией 5-го порядка, который может быть получен поворотом основного дерева вокруг его основания:
In[15]:=
Out[17]=
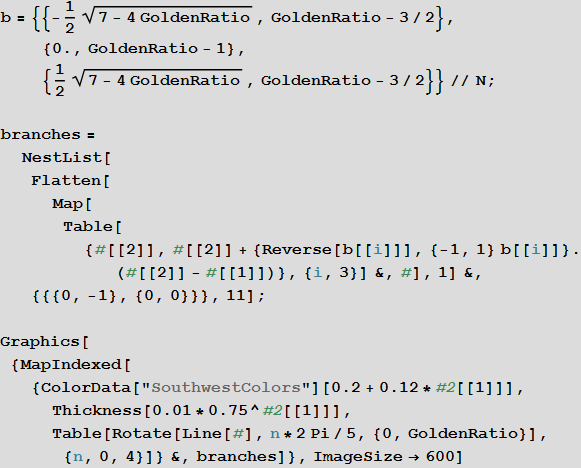
Или же можно создать аналогичный узор, вращая дерево вокруг его основной вершины:
In[18]:=
Out[20]=
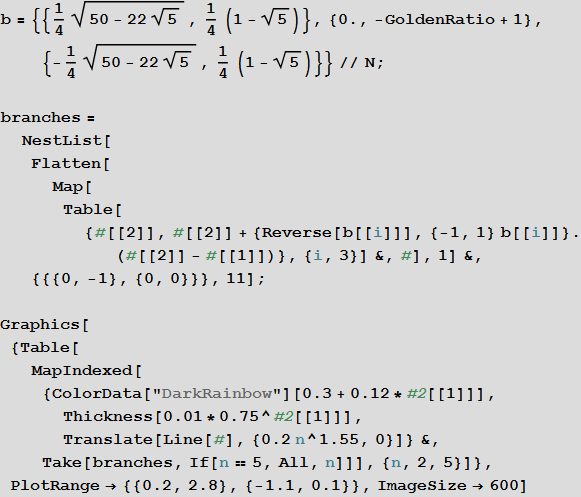
В тот же день я открыл для себя второе тройное «золотое» дерево. Это дерево, в котором центральная ветвь идёт по направлению вниз, её мы обозначим буквой D, а правая R и левая L ветви образуют угол в 36º вместе с центральной ветвью.
In[21]:=
Out[23]=
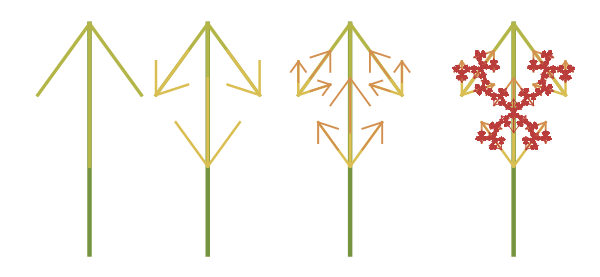
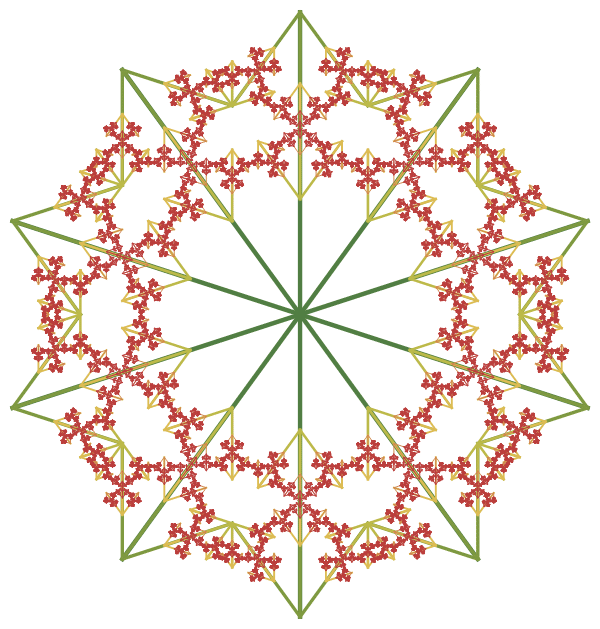
В этом случае, мы можем создать узор с осевой симметрией 10-го порядка, вращая созданное дерево вокруг его основания:
In[24]:=
Out[26]=
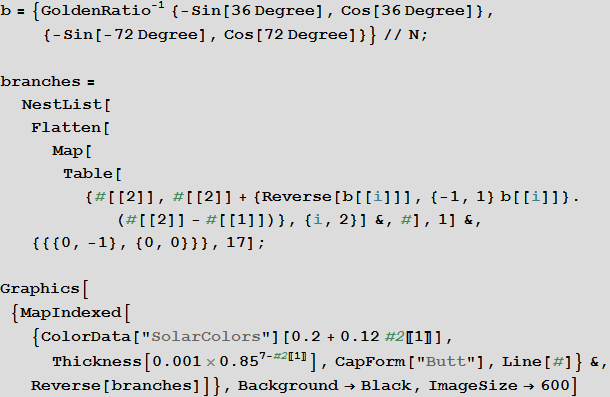
Теперь позвольте представить вам самое первое «золотое» дерево, которое я открыл для себя ещё в 2011 году:
In[27]:=
Out[29]=
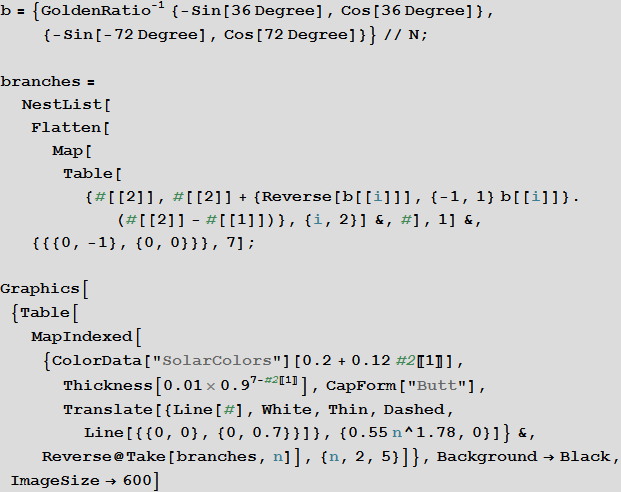
Это бинарное дерево асимметрично. В нём длина ветвей, которые отходят налево, на каждом шаге умножается на коэффициент 
, при этом они образуют с продолжением центральной ветви угол в 36º. Ветви, отходящие направо устроены таким образом, чтобы формировать правильные пятиугольники. Первые четыре итерации приведены ниже:
In[30]:=
Out[32]=
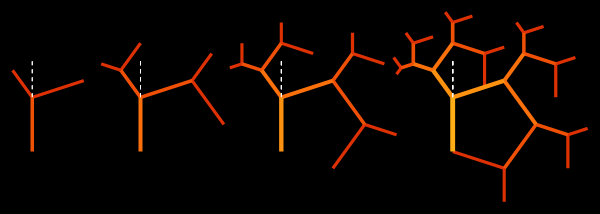
Ещё можно рассмотреть асимметричное дерево, приведённое ниже, которое имеет зеркальную симметрию относительно прямой, проходящей через центральную ветвь:
In[33]:=
Out[37]=
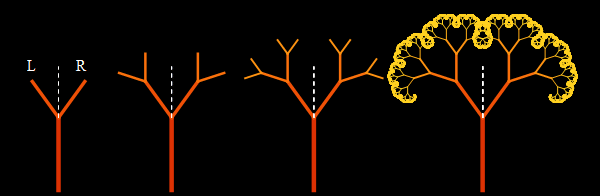
На основе этого дерева можно создать фрактал, имеющий осевую симметрию 5-го порядка:
In[38]:=
Out[42]=
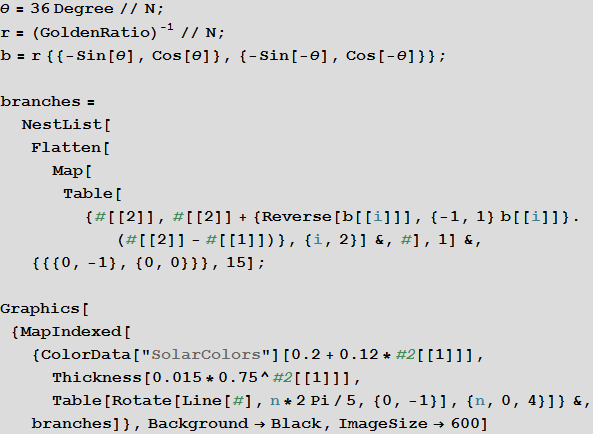
Настоящая магия произошла после того, как я «сложил» это дерево так, как это показано в этой gif-анимации, созданной с помощью Mathematica.
Когда ветви были полностью сложены, вершины дерева образовали «золотую» снежинку Коха. Золотое сечение «выстроило» ветви таким образом, что они сформировали «золотые треугольники» и «золотые гномоны», которые можно увидеть при любой степени увеличения изображения.
In[43]:=
Out[43]=
(посмотреть интерактивную демонстрацию CDF)
После того, как были рассмотрены деревья, у которых концы материнских ветвей движутся четко вдоль отрезка прямой, появилось целое семейство самокасающихся бинарных деревьев (об этом вы можете подробнее прочесть в посте «Автоматическое рисование в Mathematica: Драконовы деревья»).
Затем я начал рассматривать деревья, имеющие более двух ветвей, отходящих от основной ветви. Сборник «Фрактальных мозаик» Роберта Фатхауэра (Robert Fathauer) вдохновил меня на поиск способа отображения всех возможных деревьев, порождающих снежинки Коха, подобно тому дереву, что было рассмотрено ранее, с помощью одной диаграммы. Эта диаграмма была представлена на прошлогодней конференции Bridges conference (статью вы можете найти по ссылке, сама диаграмма — рисунок с подписью figure 4). Эти исследования и наблюдения позволили мне продвинуться вперед и обобщить симметричные самокасающиеся бинарные фрактальные деревья, изученные Бенуа Мандельбротом (Benoit Mandelbrot) и Майклом Фрэймом (Michael Frame) (см. [1]), Тарой Тэйлор (Tara Taylor) (см. [2] [3]), Душаном Пагоном (Dušan Pagon) (см. [4]) и Стивеном Вольфрамом (Stephen Wolfram) (см. [5]). После долгой работы над выяснением того, как связаны между собой «адреса» путей до вершин дерева, в которых оно касается само себя, с углом θ, а также с количеством ветвей дерева, с помощью системы Mathematica мне удалось получить все девять типов уравнений, которые определяют коэффициент самокасания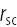 
для n-арных симметричных фрактальных деревьев. Я не буду вдаваться в подробности здесь — вы можете сами изучить самокасающиеся деревья в манипуляторе ниже. Если же вас заинтересовал данный вопрос, вы можете прочитать пост «Девять уравнений, чтобы править ими всеми. Всё семейство фракталов Серпинского» (Nine equations to rule them all. The Sierpinski«s whole family), который был написан для Wolfram Community. В этом посте получены результаты, которые были затем опубликованы в журнале Symmetry (Volume 24, Numbers 1–4, pages 320–338, 2013).
In[44]:=
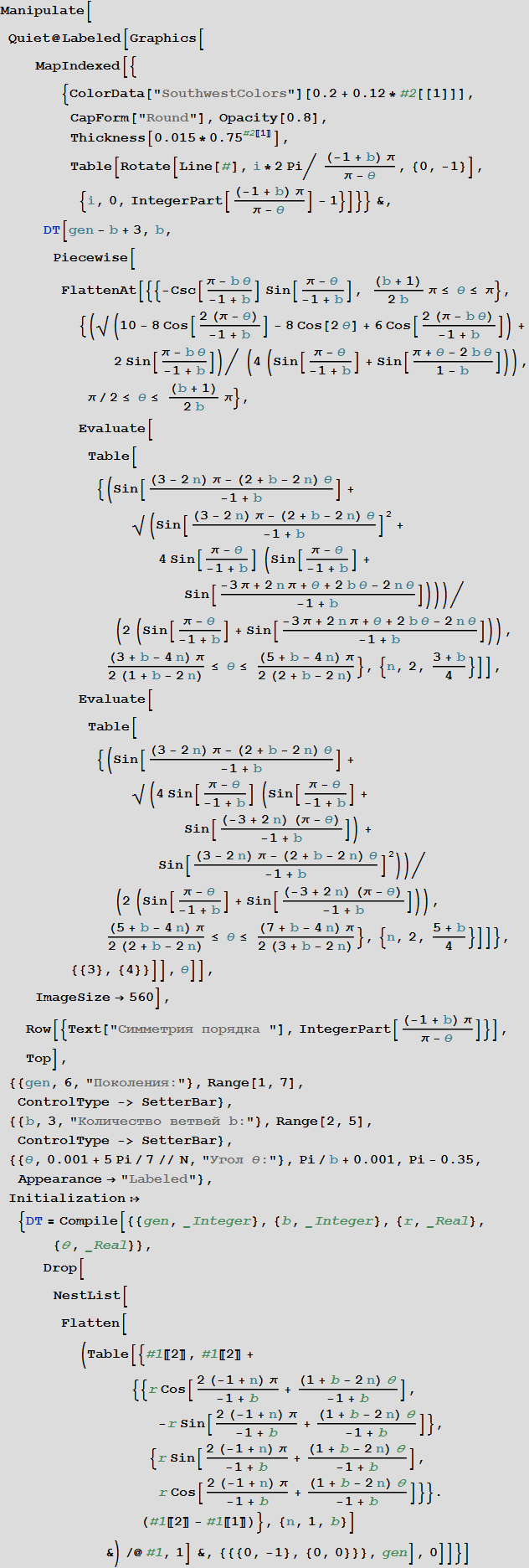
Out[44]=
(посмотреть интерактивную демонстрацию CDF)
Мои исследования не закончились на этом. Прошлым летом, во время первой недели моего пребывания на летней школе Wolfram Science Summer School, я имел счастье открыть пять трёхмерных самокасающихся бесконечных «золотых» деревьев с ветвями, направленными вниз (ниже вы можете видеть одно из таких деревьев, порождающих трёхмерную снежинку кода, которое может быть получено, если взять угол наклона боковых ветвей относительно продолжения центральной ветви равным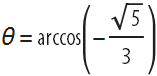 
). Этот момент стал для меня самым выдающимся.
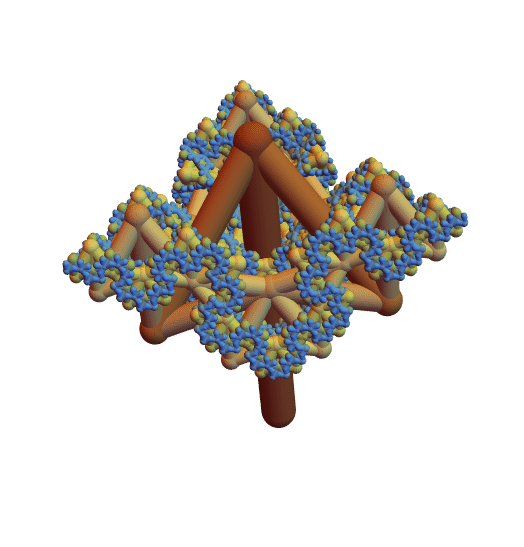Когда я приехал на летнюю школу Wolfram Science Summer School, у меня уже было некоторое смутное видение того, о чём я буду делать проект. Я хотел обобщить уравнения, которые я нашёл для двумерных фрактальных деревьев для трёхмерного случая. Я пробовал проделать это и ранее, но у меня были определённые трудности в применении всевозможных вращений, и я мог создать лишь небольшой набор высокосимметричных деревьев, подобных тетраэдрическому дереву, которое я напечатал на 3D-принтере непосредственно перед тем, как присоединиться к летней школе. Демонстрация «Ветвление деревьев в 4D» Тода Роуланда (Todd Rowland), академического директора летней школы, помогла мне понять основные идеи реализации моего проекта, а мой руководитель, Виталий Кауров (Vitaliy Kaurov), был очень вдохновлен моей целью.
После моего первого разговора со Стивеном Вольфрамом (Stephen Wolfram), все были согласны, что я должен остаться в том же самом Математическом лесу, из которого я пришел и должен постараться перейти к более высокой размерности рассматриваемых деревьев. На протяжении моей первой недели я искал литературу о трёхмерных фрактальных деревьях, и я нашел статью «Симметричные трёхмерные фрактальные деревья» (Symmetric Fractal Trees in Three Dimensions), написанную Фронгилло (Frongillo) и др., а также пример Пола Ниландера (Paul Nylander) генерирования трёхмерных тернарных фрактальных деревьев. После этого я быстро попытался воспроизвести и расширить результаты, представленные в статье, основываясь на моей интуиции и знаниях, полученных во время изучения двумерных деревьев под руководством Сюзанны Кромкер (Susanne Krömker) в Гейдельбергском университете. Окончательные результаты были поразительны и я по-прежнему поражаюсь насколько быстро все эти уравнения были получены всего за три недели. Конечно, та атмосфера, которая стояла в летней школе стала лучшим помощником для выполнения такого проекта.
«Простые правила, применяющиеся бесконечное число раз, являются неиссякаемым источником чудес» — Benoit B.Mandelbrot
In[45]:=
Out[45]=
(посмотреть интерактивную демонстрацию CDF)
(Манипулятор, созданный с помощью функции Manipulate, который вы видите выше, позволит вам изучить «лес» симметричных бинарных фрактальных деревьев. Синяя «карта» на заднем плане представляет собой множество Мандельброта для симметричных бинарных деревьев. В данном случае, множества Жулиа, связанные с этой «картой», являются множествами вершин соответствующих деревьев. Эта «карта», открытая Майклом Барнсли (Michael Barnsley), имеет некоторые общие свойства с точечными картами, открытыми Стивеном Вольфрамом (Stephen Wolfram). Мнимая ось направлена на этом рисунке вверх для того, чтобы деревья «росли» вверх. При этом белая область в центре соответствует тем положениям материнских ветвей, при которых полученные на их основе деревья являются несвязными.)
