[Перевод] Построение кроссвордов с помощью языка Wolfram Language (Mathematica)
Перевод поста Майкла Тротта (Michael Trott), «Constructing Crossword Arrays Faster».Скачать перевод в виде документа Mathematica, который содержит весь код использованный в статье, можно здесь.В главе 6 моей книги Mathematica GuideBook for Programming, в качестве примера работы со списками я обсудил то, как построить массив, представляющий собой кроссворд. Хотя этот пример был хорош для демонстрации продвинутой работы со списками, тем не менее, использование списков не является оптимальным путем построения массива кроссворда. Сложность добавления нового слова в массив с уже размещенными n-1 словами составляла для этого алгоритма 
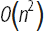, таким образом общая сложность составления массива кроссворда из n слов становилась равной 
.
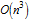На протяжении последних нескольких лет, некоторые пользователи Mathematica спрашивали меня о том, можно ли построить более быстрый алгоритм. Ответ — да, можно. Если мы будем применять методы хеширования, то мы сможем быстро и за одно и тоже время проверять, можно ли использовать некоторый элемент массива и, следовательно, мы сможем снизить общую сложность алгоритма с 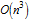до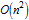 
, что для кроссвордов из тысяч слов даст большую разницу во времени, затрачиваемом на вычисления. Этот алгоритм реализован в данной статье. Когда мы размещаем отдельные буквы слова в некоторой прямоугольной таблице необходимо рассматривать множество различных ситуаций. В результате в статье содержится большее, чем обычно, количество процедурного кода. Хотя некоторые определения функций несколько длинные, благодаря комментариям между шагами вычислений и ветками решений код должен быть довольно простым для чтения и понимания.Для того, чтобы статья была самодостаточна, мы не будем использовать никакие алгоритмы, реализованные в GuideBook.
Вот формулировка задачи, которую мы будем решать:
Предположим, что нам дан список слов в виде строк. Наша задача заключается в том, чтобы вставить их в прямоугольную таблицу, состоящую из квадратов таким образом, чтобы каждое слово было расположено горизонтально (читалось слева-направо) или вертикально (читалось сверху-вниз), при этом слова должны соединяться в квадратах, содержащих одинаковые для них буквы.
Вот пример, который использует фамилии ученых (граждан СССР и России), ставших нобелевскими лауреатами. (В остальной части статьи, мы будем использовать в качестве примеров слова, имеющие прямое отношение к Mathematica.)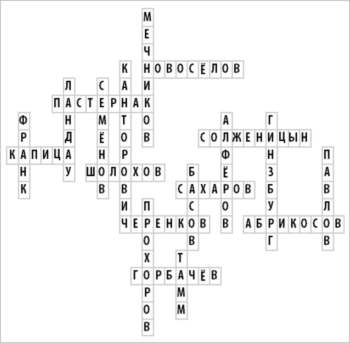
Для улучшения читаемости кроссворда, мы потребуем также, чтобы любые два горизонтальных или любые два вертикальных слова были отделены друг от друга по меньшей мере одним пустым квадратом. В дополнение к этому, никакое горизонтальное слово не должно начинаться или заканчиваться в квадрате, который соседствует с квадратом, занятым буквой вертикального слова, и, аналогично, никакое вертикальное слово не должно начинаться или заканчиваться в квадрате, который соседствует с квадратом, занятым буквой горизонтального слова. (Иными словами, квадраты, примыкающие слева и справа к горизонтальному слову и квадраты, примыкающие сверху и снизу к вертикальному слову должны оставаться пустыми.) Однако, мы разрешаем словам начинаться или заканчиваться в квадратах, занятых другим словом.
Мы будем располагать все слова в квадратной таблице (не ограниченной по размеру), построенной из отдельных квадратов и будем отслеживать содержимое каждого квадрата.
Функция
positionAWord[characterList, k,{i0, j0}, hv]
располагает список символов characterList таким образом, что k-й элемент списка будет располагаться в квадрате {i0, j0} и слово characterList будет расположено в соответствии со значением параметра hv (горизонтально или вертикально, что будет отмечаться »↔» или »↕», соответственно). Мы будем использовать конструкцию вида C[data] для того, чтобы задавать текущий статус квадрата, при этом возможны следующие ситуации:
C[] — квадрат должен оставаться пустым; C[«char»] — квадрат содержит символ char и является частью горизонтального или вертикального слова. C[«char»,»↔»] — квадрат содержит символ char в вертикальном слове и может быть использован также в горизонтальном слове. C[«char»,»↕»] — квадрат содержит символ char в горизонтальном слове и может быть использован также в вертикальном слове. C[_,»↔»] — квадрат не содержит пока что никаких символов и может быть использован в горизонтальном слове. C[_,»↕»] — квадрат не содержит пока что никаких символов и может быть использован в вертикальном слове. Вся эта информация будет ассоциирована с down values функции status. При этом status[{i, j}] будет вычислять текущее состояние квадрата с центром в точке {i, j}. На выходе она выдаст объект вида C[…] или останется в невычисленном виде, если квадрат еще не был использован каким либо способом или же не является соседом для некоторого из уже расположенных в таблице слов.Мы свяжем значение этой функции с текущим содержимым квадратом посредством выражения status[square]=value. Это позволит нам зафиксировать время поиска статуса каждого из нужных квадратов с помощью вычисления выражения status[square].
Функция positionAWord устанавливает значения квадратов в которых размещены символы слова, а также добавляет информацию о потенциальном использовании соседних квадратов в будущем. Например, квадраты расположенные непосредственно над или под горизонтально расположенным словом могут быть в будущем использованы только для вертикальных слов.
Необязательный последний аргумент функции positionAWord служит для создания возмножных побочных эффектов, таких как, скажем, мониторинг порядка добавления слов, который мы будем использовать ниже. В реализации этой функции пришлось рассмотреть большое количество различных ситуаций — это легко увидеть в комментариях к коду ниже.
In[1]:=
В качестве примера, мы расположим слово Mathematica, начиная с квадрата {1,1} горизонтально.
In[2]:=
Ниже приведен список квадратов, которые были помечены.
In[3]:=
Out[3]=
Для того, чтобы увидеть вживую процесс построения, создадим функцию makeCWPGridGraphics, которая будет ракрашивать квадраты в соответствии с их текущим статусом.
In[4]:=
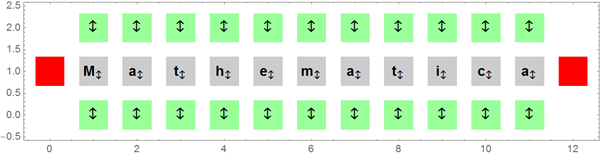
Приведенный ниже график показывает текущий статус квадратов, соседствующих с уже расположенными по квадратам символами.
In[5]:=
Out[5]=
Функция
positioningAWordIsPossibleQ[characterList, k,{i0, j0}, hv]
проверяет, возможно ли список символов characterList расположить таким образом, чтобы k-й элемент списка располагался в квадрате {i0, j0}, а слово characterList было расположено в соответствии со значением параметра hv (горизонтально »↔» или вертикально »↕»). Для того, чтобы сделать это нам потребуется проверить, чтобы каждый из необходимых квадратов был либо доступен, либо же имел необходимый символ уже на месте. Также, соседние квадраты должны быть либо пусты, либо должны иметь буквы из уже расположенного перпендикулярно слова. Вспомогательная функция whileTrueLoops является итеративной функцией, которая заканчивает свою работу, как только с помощью техники Throw-Catch найден первый несовместимый квадрат. В дальнейшем мы всегда будем предполагать, что новое слово размещается только с помощью функции positionAWord и только тогда, когда функция positioningAWordIsPossibleQ выдает значение True.
In[6]:=
In[8]:=
Если мы уже расположили слово Mathematica горизонтально, мы можем расположить еще одну копию слова Mathematica вертикально.
In[9]:=
Out[9]=
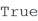
Но мы не можем расположить горизонтально слово Mathematica в той же позиции.
In[10]:=
Out[10]=
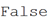
В целом, можно было бы поместить другую копию вдоль уже расположенной, начиная с буквы «t» в позиции {3, 3}.
In[11]:=
Out[11]=
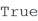
Конечно, мы могли бы поместить другую копию слова Mathematica посередине, скажем, сделать ее вертикальной, проходящей через вторую букву «m» горизонтальной копии слова Mathematica.
In[12]:=
Out[12]=
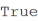
In[13]:=
С помощью кода ниже мы можем наглядно отобразить текущее состояние нашей таблицы.
In[14]:=
Out[14]=
Функция
findAPossiblePositionAndPositionAWord[characterList]
ищет возможное расположение символов слова characterList и затем размещает их. Функция возвращает либо координаты добавляемого символа, либо $Failed, в случае, если никакого способа добавить слово нет. Мы также снабдили эту функцию несколькими довольно очевидными опциями, которые, среди прочего, позволяют располагать слова либо настолько плотно, насколько это возможно, либо наоборот — максимально свободно. Если значение опции AttachmentPosition сделано равным Inner, то функция стремится добавлять каждое новое слово внутри уже размещенных, значение Outer — наоборот, если же используется значение RandomSample, то позиция нового слова выбирается случайным образом.
In[15]:=
In[16]:=
In[17]:=
Наконец, мы создади функцию makeCWPGrid[status], которая будет конструировать, собственно, таблицу из букв на основе down values функции status.
In[18]:=
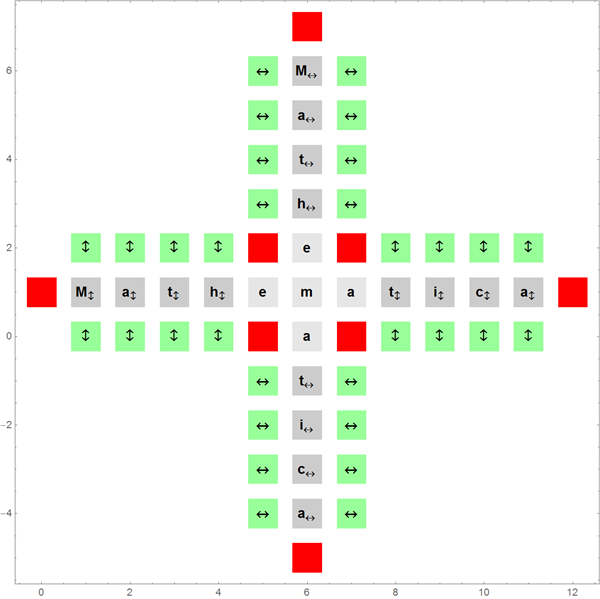
График ниже показывает состояние всех уже добавленных квадратов после того, как слово Mathematica было добавлено 6 раз к первоначальному. Серые квадраты соответствуют уже окончательно размещенным словам; красные — должны оставаться пустыми; зеленые — через них могут быть добавлены новые слова. Стрелками показано в каком направлении можно добавить новые слова.
In[19]:=
Out[22]=
In[23]:=
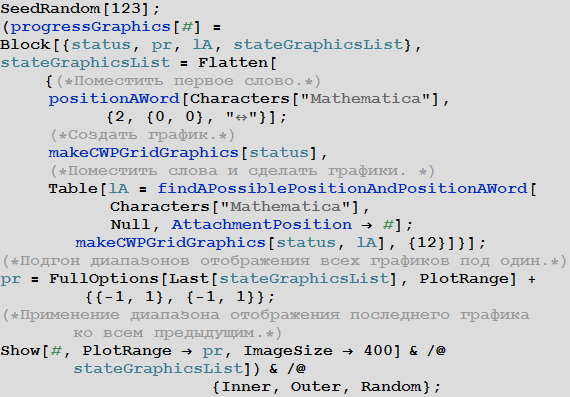
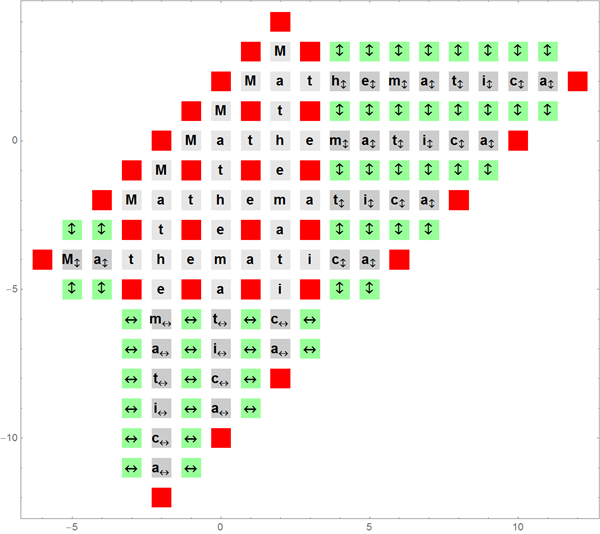
График ниже демонстрирует некоторые шаги процесса построения массива кроссворда. Если внимательно изучить устройство квадратов в каждом из рисунков (для каждой из опций), станет намного более понятно то, как устроены алгоритмы, представленные выше.
In[25]:=
Out[25]=
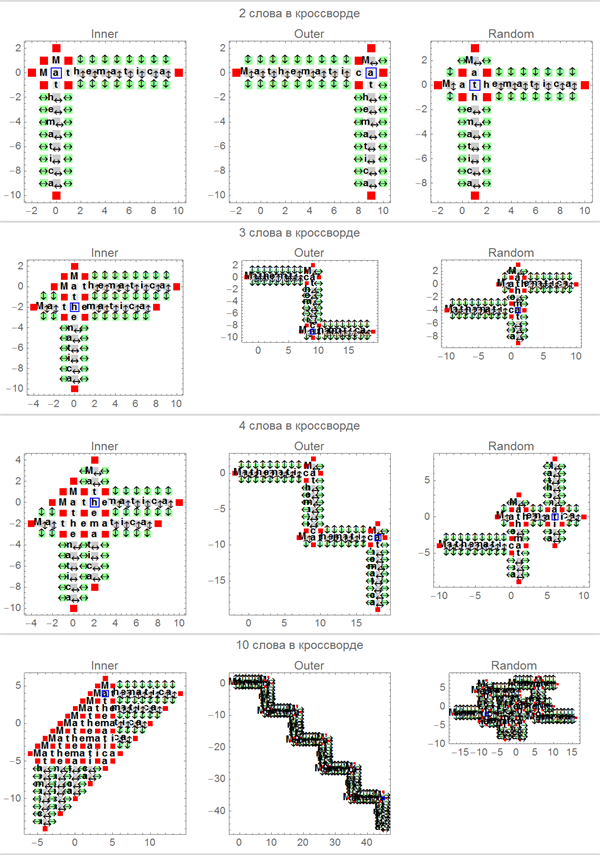
Применяя функцию Manipulate, мы можем с легкостью создать интерактивную версию алгоритма, которая позволит нам проследить за его шагами наглядно и просто. Приведенная ниже интерактивная версия алгоритма позволяет проследить за 12 его первыми шагами для различных значений опций.
In[26]:=
Out[26]=
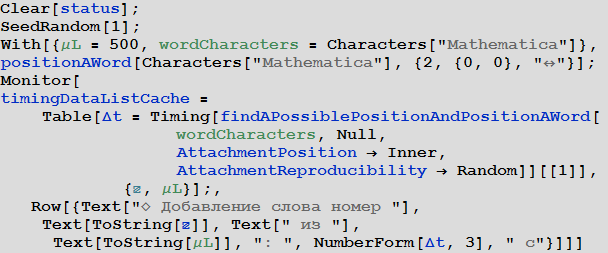
Теперь давайте рассмотрим сложность реализованного метода. Ввиду того, что поиск текущего состояния квадрата является почти постоянной величиной (не зависящей от количества уже заданных квадратов), мы ожидаем линейную сложность O (n) в зависимости от количества слов. В качестве теста, мы найдем размещение 500 слов Mathematica. Для визуализации процесса вычислений мы будем использовать функцию Monitor.
In[27]:=
Теперь изобразим измеренные значения затраченного времени. График справа показывает среднее время на добавление заданного количества слов. Он растет линейно с числом слов, которые необходимо добавить.
In[30]:=
Out[30]=
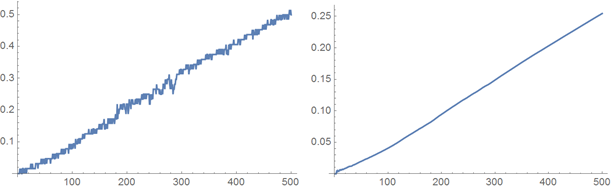
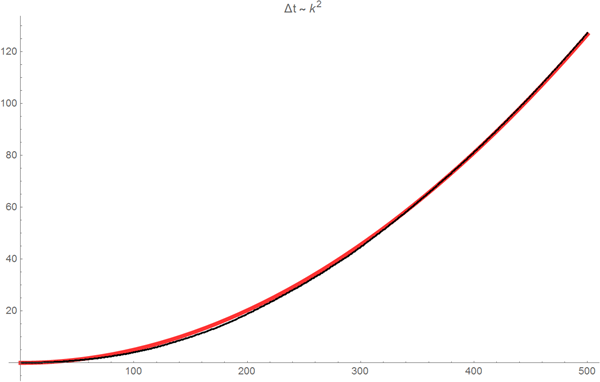
Таким образом, суммарное время формирования массива кроссворда из n слов имеет сложность порядка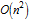 
. График показанный ниже наглядно демонстрирует это (черный — затраченное время, красный — найденная модель вида 
).
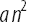In[31]:=
Out[32]=
Ниже представлен полученный массив кроссворда. Мы используем небольшой размер шрифта для того, чтобы отобразить его здесь полностью.
In[33]:=
Out[33]=
Благодаря намного большей скорости работы этого подхода, основанного на хешировании для большого числа слов (скажем, тысяч), мы теперь можем очень быстро составить кроссворд, скажем, из 250 слов. При этом в качестве списка этих слов возьмем 250 выбранных случайно встроенных функций языка Wolfram Language (системы Mathematica).
In[34]:=
Out[38]=
In[39]:=
Out[39]=
График, показанный ниже отображает порядок в котором слова были расположены на плоскости (в таблице). Красные, высокие столбцы соответствуют словам, которые были добавлены в начале, синие, низкие «башенки» — добавленным позже.
In[40]:=
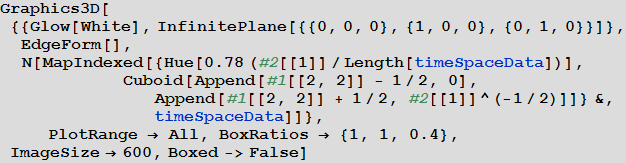
Out[40]=
Теперь построим массив кроссорда, состоящего из названий функций (и их опций), связанных с различными визуализациями в языке Wolfram Language.
In[41]:=
Out[42]=
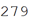
In[43]:=
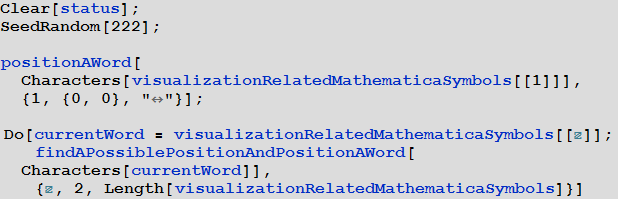
In[47]:=
Out[47]=
Теперь создадим функцию потенциала f для функции positionAWord. Эта функция будет использоваться для определения того, какому именно уже расположенному слову принадлежит тот или иной символ.
In[48]:=
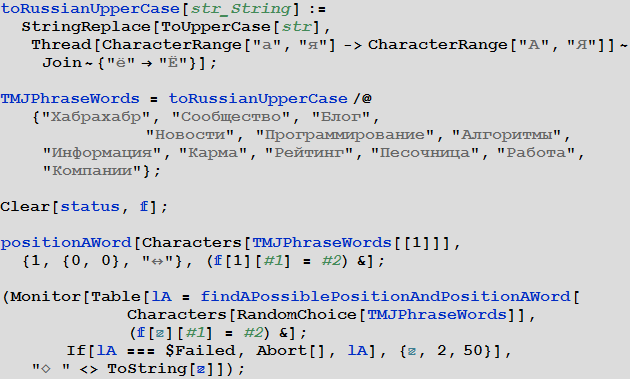
Создадим теперь некоторую вариацию функции makeCWPGrid, которая будет использовать информацию связанную с функцией f для раскрашивания слов.
In[53]:=
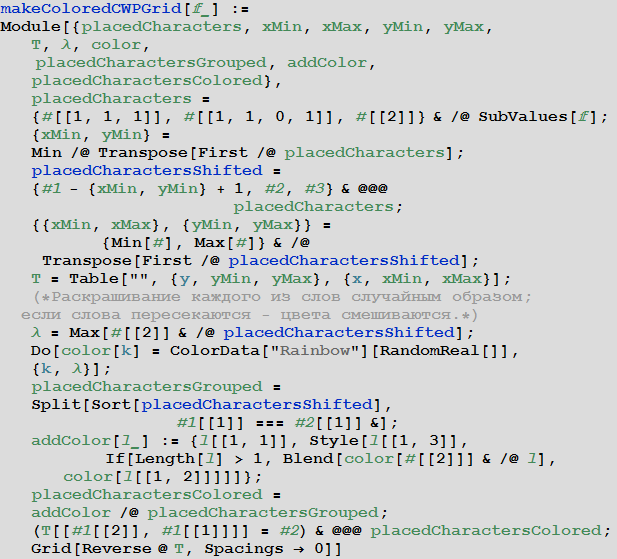
Результат представлен в таблице ниже. Цвет букв стоящих на пересечении слов смешивается.
In[54]:=
Out[54]=
Мы закончим статью, создав единую функцию CrossWordConstructionCached, которая служит для создания кроссворда на основе списка слов, который подается ей на вход.
In[55]:=
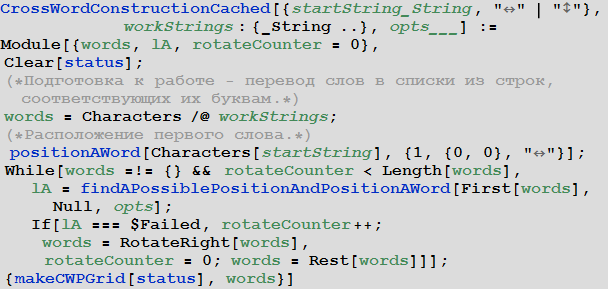
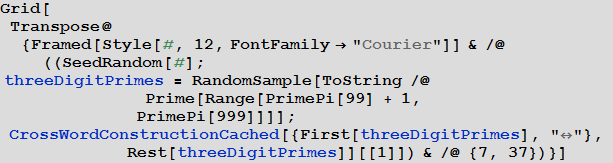
Построенный алгоритм может работать с любыми символами. В качестве примера можно привести два способа составить кроссворд из всех трехзначных простых чисел.
In[56]:=
Out[56]=
Или же можно создать кроссворд из фамилий всех нобелевских лауреатов (граждан России и СССР):
In[57]:=
Out[58]=
