[Перевод] Почему самые сложные уравнения физики такие трудные?
Уравнения Навье-Стокса описывают простые повседневные явления, вроде воды, текущей из садового шланга — однако на них основана задача, решение которой оценили в миллион долларов

В физике есть уравнения, описывающие всё, от растяжения пространства-времени до полёта фотона. Однако же лишь один набор уравнений считается настолько математически сложным, что его выбрали в роли одной из семи «Задач тысячелетия», за решение которых Математический институт Клэя предлагает премию в миллион долларов: это уравнения Навье-Стокса, описывающие течение жидкостей.
Недавно я писал о том, как для этих уравнений был получен новый важный результат. И эта работа свидетельствует о том, что прогресс на пути к «премии тысячелетия» будет более тяжёлым, чем ожидалось. Почему же эти уравнения, описывающие такие знакомые явления, как вода, текущая по шлангу, математически понять гораздо сложнее, чем, допустим, уравнения поля Эйнштейна, включающие в себя такие ошеломляющие объекты, как чёрные дыры?
Ответ, как я понял, кроется в турбулентности. Это явление испытывали мы все, в полёте в неоднородном воздухе на высоте в 10 000 м, или при наблюдении за воронкой от уходящей в слив воды в ванне. Однако из осведомлённости не следует познание: турбулентность — одна из наименее понятных областей физического мира.
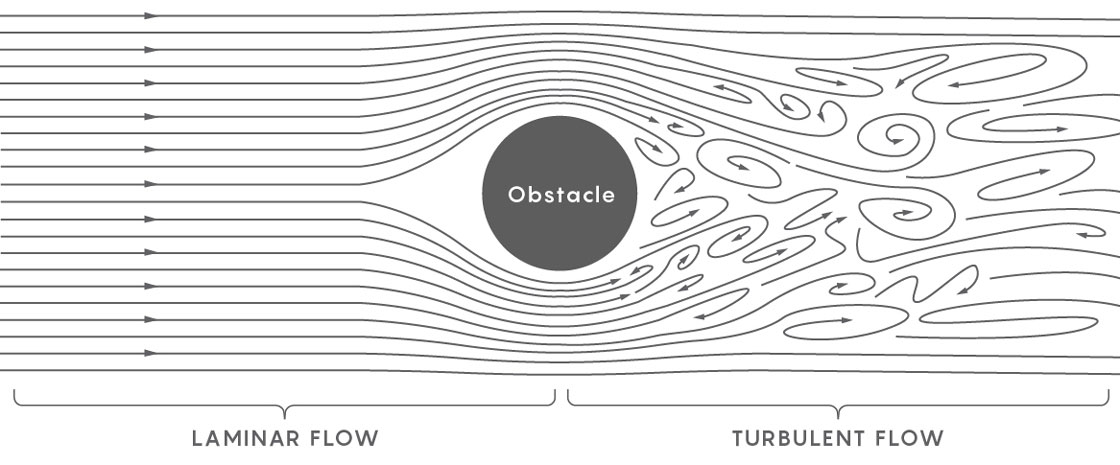
Пример потока без турбулентности — это спокойная река. Каждая её часть движется в одном и том же направлении с одной и той же скоростью. Турбулентная жидкость появляется, когда поток реки ломается так, что разные части потока начинают двигаться в разных направлениях с разными скоростями. Физики описывают формирование турбулентности сперва как появление воронки в гладком потоке, а затем как формирование мелких воронок в первой воронке, и ещё более мелких воронок в этих воронках — море воронок, уходящих внутрь жидкости, так, что жидкость разбивается на дискретные части, каждая из которых взаимодействует друг с другом и движется в своём собственном направлении.
Исследователи хотят понять, как именно гладкий поток разбивается на турбулентные завихрения, и смоделировать будущую форму жидкости, после того, как турбулентность взяла своё. Но Задача тысячелетия формулируется более скромно: нужно лишь доказать, что решения всегда существуют. То есть, вопрос в том, могут ли уравнения описать любую жидкость, с любыми начальными условиями, и до бесконечно далёкого будущего?
«Первый шаг — просто попытаться доказать, что у уравнений есть какие-то решения, — говорит Чарли Фефферман, математик из Принстонского университета. — Это не даёт настоящего понимания поведения жидкостей, но если у вас и этого нет, то вы вообще ничего не знаете».
Так как можно доказать существование решений? Начать нужно с того, чтобы понять, из-за чего их может не оказаться. Уравнения Навье-Стокса подразумевают подсчёт изменения таких величин, как скорость и давление. Математиков беспокоит следующий вариант развития событий: вы прогоняете эти уравнения, и через какое-то конечное время они сообщают вам, что частица жидкости движется с бесконечной скоростью. А это проблема — подсчитать изменение бесконечного значения не проще, чем поделить на ноль. Математики называют такие ситуации «взрывом», и в случае взрыва уравнения перестают работать и решений не находится.

Уравнения Навье-Стокса описывают поток несжимаемой жидкости.
В целом произведение массы (голубая часть) на ускорение (фиолетовая) приравнивается к силам, действующим на жидкость (оранжевая):
- ρ — плотность жидкости;
- dV/dt — изменение скорости по времени;
- V ∇V — скорость и направление движения;
- ∇P — изменение внутреннего давления;
- ρ g — влияние внешних сил (к примеру, гравитации);
- μ ∇2V — влияние внутренних сил (вязкость).
Доказательство отсутствия взрывов (и существования решений) равносильно доказательству того, что максимальная скорость любой частицы жидкости остаётся ограниченной неким конечным значением. Одной из наиболее важных величин оказывается кинетическая энергия жидкости.
Когда вы начинаете моделировать поток при помощи уравнений Навье-Стокса, у вашей жидкости есть некое начальное количество энергии. В турбулентных потоках энергия может начать концентрироваться. Вместо того, чтобы равномерно распространяться по всей реке, кинетическая энергия может собираться в водоворотах произвольно малого размера, и частицы в этих водоворотах (теоретически) могут разогнаться до бесконечной скорости.
«При переходе на всё меньшие и меньшие масштабы, кинетическая энергия становится всё менее и менее полезной для контроля решения. Решение может делать, что угодно, и я не буду знать, как его контролировать», — говорит Влад Викол, математик из Принстонского университета, написавший новую работу вместе с Тристаном Бакмастером.
Математики классифицируют частично дифференциальные уравнения на основании того, до какой степени они могут начать вести себя плохо на бесконечно малых масштабах. Уравнения Навье-Стокса находятся на экстремальном конце этой шкалы. Сложность математики уравнений в каком-то смысле отражает сложность турбулентных потоков, которые они должны уметь описывать.
«Когда вы увеличиваете масштаб в каком-то месте, то с математической точки зрения вы теряете информацию о решении, — говорит Викол. — Но турбулентность должна описывать именно это — передачу кинетической энергии от крупных ко всё более мелким масштабам, поэтому она прямо-таки просит вас увеличивать масштаб».

Говоря о математических свойствах физических уравнений, естественно задаться вопросом:, а изменят ли эти рассуждения то, как мы расцениваем физический мир? В случае с уравнениями Навье-Стокса и Задачей тысячелетия ответ будет одновременно «да» и «нет». После почти 200 лет экспериментов ясно, что уравнения работают: течение, предсказанное Навье-Стоксом, последовательно совпадает с течением, наблюдаемым в экспериментах. Если вы — физик, работающий в лаборатории, вам этого может быть достаточно. Но математикам нужно знать больше — они хотят проверить, можно ли следовать этим уравнениям до упора, чтобы следить за тем, как именно меняется поток, от одного момента времени к другому (для любой начальной конфигурации жидкости), и даже уловить источник турбулентности.
«Поведение жидкостей таит в себе сюрпризы, — говорит Фефферман. — Эти сюрпризы в принципе объясняются фундаментальными уравнениями, управляющие потоками жидкостей, но как перейти от уравнений, управляющих движением жидкости, к описанию того, как на самом деле движется жидкость — это загадка».
