[Перевод] Почему на то, чтобы найти точное значение постоянной Планка, понадобилось 100 лет?

Перевод поста Майкла Тротта (Michael Trott) «An Exact Value for the Planck Constant: Why Reaching It Took 100 Years».
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Полине Сологуб за помощь в переводе и подготовке публикации
Содержание
— Некоторые мысли по случаю Всемирного дня метрологии в 2016 году
— Введение и немного обо мне
— От истоков метрической системы до сегодняшних дней.
— Увеличение числа констант
— Существующая система СИ и проблема килограмма
— Новая СИ
— Секунда
— Моль
— Кельвин
— Ампер
— Кандела
— Почему основных единиц измерения именно 7?
— Путь к изменению определения килограмма
Повествование ведется от имени Жана-Шарля де Борда.
Некоторые мысли по случаю Всемирного дня метрологии в 2016 году
Позвольте мне представиться:
Я человек науки и люблю точность.
Все это время я был где-то рядом.
Я забрал у людей фунт и туаз.
И я был рядом с Людовиком XVI
В минуты его сомнений и боли.
Я чертовски уверен в том, что метрическая рулетка,
Благодаря платиновым стандартам будет установлена раз и навсегда.
Я рад встрече с вами!
Надеюсь, вы угадали, как меня зовут?
Введение и немного обо мне
Если вы еще не догадались, я — Жан-Шарль де Борда: моряк, математик, ученый и член Академии наук. Я родился 4 мая 1733 года в городе Дакс во Франции. Две недели назад я отметил свой двести восемьдесят третий день рождения. А вот и я:
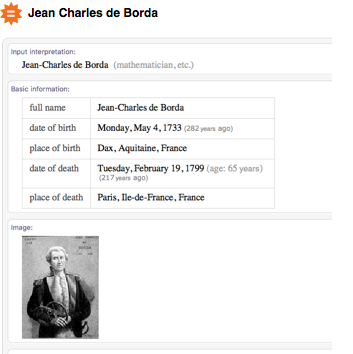
В моем родном городе в честь меня воздвигли памятник. Если вы будете неподалеку, задержитесь, чтобы посмотреть на него. Если вы не знаете, где находится Дакс, вот карта:
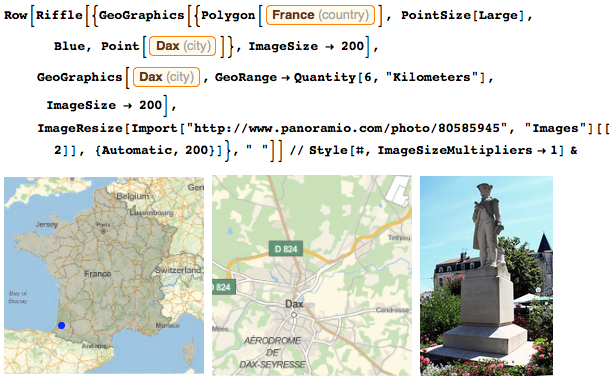
Когда я был мальчиком, Франция выглядела примерно так же, как сейчас. У нас было немного меньше территории с восточной стороны, но зато в Северной Америке моей стране принадлежал хороший кусок земли:
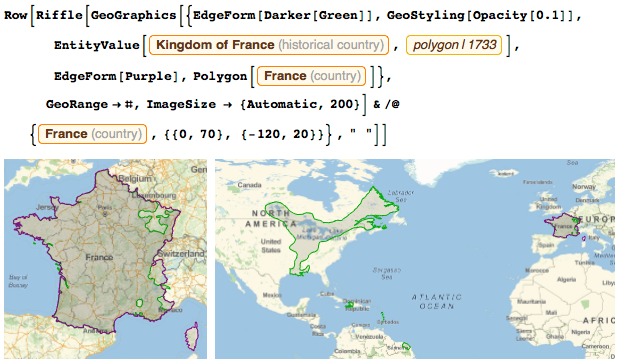
Я вел интересную жизнь. К 32 годам я провел много времени в открытом море, проводя научные исследования. Когда мне было сорок, я уже командовал несколькими кораблями в сражениях Семилетней войны (хотя большую часть своей жизни я все-таки посвятил науке).
Я умер 19 февраля 1799 года в Париже, и никто не знает, где моя могила (я-то знаю, конечно, но не могу рассказать об этом). Мое имя увековечено на северо-восточной стороне Эйфелевой башни:
На протяжении веков многие из моих коллег-французов, чьи имена присоединились к моему, говорили мне, что я заслужил место в Пантеоне. Однако вы не найдете меня ни там, ни на кладбищах Пер-Лашез, Монпарнас или Монмартр.
Но не это не дает мне покоя. Я скромный человек; не дает мне спать по ночам проблема с эталоном килограмма. Правда, скоро я смогу отдохнуть за все бессонные ночи.
Позвольте рассказать вам об этом.
Всю свою жизнь я занимался математикой, геометрией, физикой и гидрологией. Мне нравились измерения. Возможно, вы слышали о системе голосования (метод Борда) — это тоже моё изобретение. Я также значительно усовершенствовал периодический круг (repeating circle). Вот с этого-то и начинается моя история. Периодический круг сыграл решающее значение в определении точного размера Земли (обсуждение моего круга см. здесь).

Я жил во Франции во времена монархии. Это время было трудным для многих людей, и особенно — для крестьян. Отчасти так было потому, что торговля и коммерция были в упадке из-за отсутствия единой системы единиц измерения для страны в целом. Если вам нравится читать на исторические темы, я настоятельно рекомендую вам книгу Кула Люди и измерения — вы сможете представить себе, как обстояли дела с измерениями (прежде всего вес и размер) во Франции в 1790 году. Аналогичная ситуация сложилась и в других странах (см. доклад Иоганна Георга Траллеса о ситуации в Швейцарии).
В августе 1790 года по инициативе Людовика XVI я стал председателем Комиссии мер и весов. И до сих пор меня волнует тот факт, что через 1000 лет после инициативы Шарлеманя по унификации мер и весов началась новая работа в этом направлении. С помощью нашей комиссии была создана метрическая система, которая на сегодняшний день является международной системой единиц, сокращенно обозначаемой СИ (по-французски le Système international d’unités).
В комиссию также входили: Пьер-Симон Лаплас (уравнения Лапласа), Адриен-Мари Лежандр (полиномы Лежандра), Жозеф-Луи Лагранж (функция Лагранжа), Антуан Лавуазье (формулировка закона сохранения массы вещества), и Маркиз де Кондорсе (я всегда говорил Адриену Мари, что ему стоило бы заказать свой портрет, но он отнекивался, говоря, что слишком занят расчетами). За последние десятилетия Адриен-Мари подружился с Жаком-Луи Давидом, который написал целую коллекцию картин с ним; к сожалению, никто из смертных никогда не увидит их. Лагранж, Лаплас, Монж, Кондорсе и я входили в первоначальный состав команды (хотя в самом начале с нами был еще Жером Лаланд, а позже присоединился Луи Лефевр).
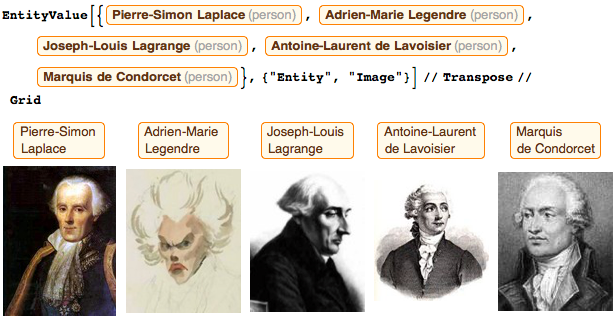
Трое из нас (Монж, Лагранж и Кондорсе) были похоронены или увековечены в Пантеоне. Я очень надеюсь на то, что в один прекрасный день к ним присоединится и Пьер-Симон, который этого заслуживает.
Как я уже говорил, французским гражданам сложно жилось в эту эпоху. Лаплас писал:
В использовании находится чудовищное количество единиц измерения; они неудобны для расчета, их трудно сравнивать; те затруднения, которые они производят в торговле, нельзя рассматривать, не признавая, что принятие измерительной системы (в которой единые ее части легко подвергаются расчету и которые получены по меньшей мере произвольно, причем единицы измерения должны быть указаны самой природой) станет одной из самых важных услуг, которые любое правительство может оказать обществу. Нация, внутри которой появится новая система мер, будет первой пожинать плоды ее преимуществ, а затем следовать ее примеру начнут и другие нации, для которых она, таким образом, станет благодетелем; медленное, но неотвратимое владычество разума, преобладающего над национальной ревностью, увенчает все преодоленные препятствия, противопоставляющие себя преимуществам.
Все пять математиков (Монж, Лагранж, Лаплас, Лежандр и Кондорсе) внесли исторически значимый вклад в математику. Их именами названы математические теоремы, структуры и операции:


В 1979 году Рут Инес Шампань написал диссертацию о влиянии пяти моих сограждан в создании метрической системы (чтобы узнать подробнее о вкладе Лежандра, см. статью Дорис Хеллман). Мне кажется, что на сегодняшний день математики в большинстве своем не интересуются больше единицами измерения, а движущей силой в этой области являются физики. Но я сделал, как в статье Теодора П. Хилла о методе объединения вероятностных распределений, позволяющем объединить знания из различных экспериментов (сразу скажу, что у нас на небе есть мгновенный доступ к arXiv. Скажу больше: прямое соединение с arXiv стало крупнейшим нововведением прошлого тысячелетия).
Наша задача состояла в том, чтобы создать унифицированные единицы измерения времени, длины, объема и массы. Нам нужны были такие единицы измерения, с помощью которых можно было бы измерить как крошечные, так и астрономического масштаба объекты. Принципы нашего подхода были хорошо обобщены Джоном Куинси Адамсом, государственным секретарем Соединенных Штатов, в книге 1821 года »Доклад по мерам и весам».

Первоначально мы (мы называли себя metric men) предложили лишь несколько префиксов: кило-, дека-, гекто-, деци-, санти-, милли- и мириа-, которая больше не используется (в некоторых старых книгах можно найти примеры использования приставки, означающей десять тысяч).
Эта идея использования префиксов довольно рано возникла в процессе разработки новых единиц измерения. Вот наши предложения 1794 года:

В свое время мы также использовали деми- и дабл- (деми-гектолитр (= 50 литров) или двойной декалитр (= 20 литров)).
Время, длина и масса, измеряемые в физике, химии и астрономии, охватывают более 50 порядков. И единицы, созданные нами в бурную эпоху французской революции, выдержали испытание временем:


В будущем для СИ, возможно, потребуется еще несколько префиксов. В недавно открытой обсерватории LIGO длина плеч интерферометра изменялась приблизительно на 10 йоктометров. Датчики массы с разрешением в йоктограммах уже существуют. Один йоктометр равен 10–24 метра. Человечество уже может измерять крошечные силы порядка зептоньютонов.
С другой стороны, астрономии нужны префиксы больше, чем 1024. И однажды они могут стать официальными.

Я человек строгих правил. Меня сводит с ума, когда в двадцать первом веке я вижу людей, которые не соблюдают правила использования префиксов СИ. Недавно я видел, как кто-то пишет на доске, что год состоит из из π декамегасекунд (π daMs):

Пускай это даже хорошее приближение (с отклонением всего 0,4%); только вот когда этот человек узнает, что не следует объединять префиксы?
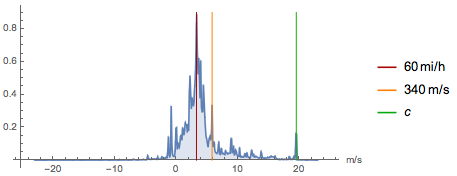
Технологический прогресс в течение последних двух столетий шел быстро. И префиксы мега-, гига-, тера- или нано-, пико- и фемто- в двадцать первом веке стали общеупотребительными. Ниже вы видите вероятностное распределение значений скорости. Некоторые скорости (например скорость звука или скорость света) используются чаще, чем другие, однако в функции распределения можно найти много локальных максимумов:
Вот отчет (который мы предоставили в марте 1791 года), давший начало метрической системе и в котором было описано концептуальное значение метра и килограмма. Он был подписан Лагранжем, Лапласом и Монжем (теперь он доступен даже через то, что современный мир называет «идентификатор цифрового объекта», или DOI, вроде 10.3931 /е-rarа-28950):

Большинство людей думает, что основание 10 тесно связано с метром, секундой и килограммом как единицами измерения. Однако мы решили использовать 10 в качестве основы для деления единиц только 27 октября 1790 года. Мы всерьез рассматривали 12 как основу, потому что делимость на 2, 3, 4 и 6 была удобна для торговли. Сегодня ясно, однако, что мы сделали правильный выбор. Лагранж был прав, когда настаивал на том, чтобы основанием стало число 10. Во время Французской революции мы не шли ни на какие компромиссы. А 5 ноября 1792 года я предложил перевод часов в десятичную систему счисления (Даламбер предложил это еще в 1754 году, подробнее см. эту статью). Человечество оказалось не готовым к таким изменениям; может быть, в двадцать первом веке десятичные часы, наконец, будут признаны гораздо более удобными, чем 24 часа, 60 минут и 60 секунд. Наши десятичные часы были прекрасны. Для меня стало настоящим сюрпризом, что человечество до сих пор делит угол на 90 градусов. В своем периодическом круге я делил прямой угол на 100 градусов.
Мы хотели сделать новые единицы измерения действительно равными для всех людей, а не основывать их, к примеру, на длине предплечья короля. В общем, «для всех времен, для всех народов» («À tous les temps, à tous les peuples). Теперь эта мечта исполнится.
Я уверен, что наступит день, когда предсказанное Менделеевым:
Давайте облегчим всеобщее распространение метрической системы, тем самым содействуя общему благосостоянию и желаемому будущему сближению народов. Оно придет не сразу, но постепенно и совершенно точно.
станет реальностью даже в тех 3 странах мира, которые не пользуются этой системой:

Единицы СИ стали законно использоваться в США с середины двадцатого века, когда обычные для США единицы измерения стали выводиться из определений основных единиц СИ. Граждане могут выбирать, какие единицы измерения они хотят использовать для торговли.
Мы также ввели десятичное исчисление в основу денежной системы, и наш франк был в обращении с 1793 по 2002 год. На сегодняшний день все страны имеют в обращении деньги, основанные на десятичной системе исчисления. Вот «разбивка» номиналов монет по странам:

Мы совершенно серьезно говорили про «всех людей», доказательством чему служит наша работа с нашими заклятыми врагами — Великобританией и новыми Соединенными Штатами (через Томаса Джефферсона лично) по созданию новой системы единиц измерения для всех основных стран. Но, как это часто бывает, в сражении политики и разума победила политика.
Я умер 19 февраля 1799 года, всего за несколько месяцев до первых успехов нашей группы. 22 июня 1799 года мой дорогой друг Лаплас произнес речь о создании новых единиц длины и массы еще до того, как новые образцы были доставлены в архив Республики (где они и находятся до сих пор).
В случае, если читатель заинтересовался моей богатой событиями жизнью, Жан Маскарт написал в 1919 году мою биографию, доступную теперь в виде репринтного издания.
От истоков метрической системы до сегодняшних дней
Двое из моих друзей: Жан-Батист-Жозеф Деламбр и Пьер Мешен отправились во Францию и Испанию для проведения измерений, чтобы определить метр как одну десятимиллионнную расстояния от Северного полюса до экватора Земли. Я рад, что миссия была утверждена. Когда Людовик XVI одобрил финансирование миссии, он уже находился под арестом. Мой дорогой друг Лавуазье назвал свою задачу »самой важной миссией, которая когда-либо была поставлена перед человеком».

Если вы еще не прочитали книгу Кена Олдера Мера всех вещей, советую вам сделать это немедленно. Существует даже немецкий фильм о приключениях двух моих старых друзей. Вооруженные специальным инструментом, который я сконструировал для них, они проделали работу, результатом которой стало создание метра. Несмотря на то, что мы хотели установить длину метра, равную одной десятимиллионной длины половины меридиана, проходящего от полюса до экватора через Париж, я думаю, что сегодня это красивое определение исключительно концептуально. Мы не знали в то время, что Земля не совсем круглая, и ошибки в расчетах уплощения Земли привели к небольшой, но прискорбной ошибке в 0,2 мм. Вот длина половины парижского меридиана, выраженная в метрах:

Если бы учитывались все возвышенности (чего не сделали Деламбре и Мешен, потому что для этого им пришлось бы путешествовать вдоль всего меридиана, чтобы учесть каждую гору и холм!), и использовались 3D-координаты (в том числе высот местности), их метр в конечном итоге стал бы короче на 0,4 мм:

А вот профиль высоты по парижскому меридиану:
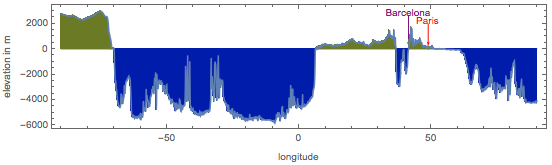
Из-за «фрактальности» поверхности Земли, если взять средство измерения ещё меньше, то ошибка значительно вырастет.
Метр окажется еще на 0,9 мм длиннее, если проводить измерения с помощью линейки длиной в несколько сотен метров:

Более реалистичным было бы следовать высоте уровня моря. Разница между полученными определениями метра составляет всего несколько микрометров:
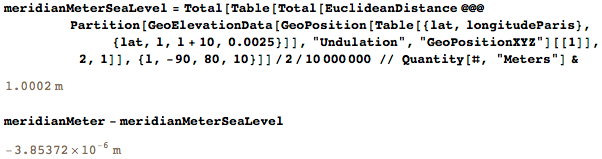
Как минимум, меридиан должен был пройти через Париж (а не через Лондон, как предлагали некоторые британские ученые моего времени). Но в любом случае, нахождение длины меридиана было всего лишь ступенькой на пути к созданию образца метра. После того, как мы получили образец, меридиан нас больше не интересовал.
Вот набросок триангуляции, проведенной Пьером и Жан-Батистом за время их авантюрной шестилетней экспедиции. Благодаря Интернету и различным французским проектам по оцифровке — франкоязычные читатели, заинтересованные в метрологии и истории, могут теперь читать о полученных результатах онлайн и воспроизводить наши расчеты:
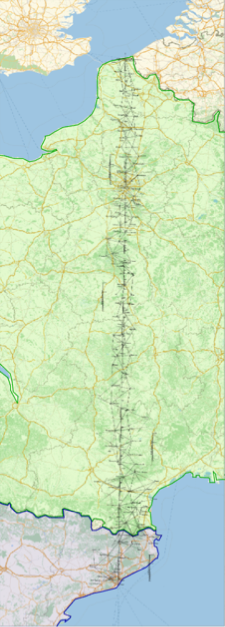
Часть Парижского меридиана (и Парижская обсерватория, отмеченная красным цветом) отмечены маркером: не пропустите их во время вашего следующего визита в Париж! Франсуа Араго переизмерил парижский меридиан. В 1804 году Лаплас получил от Наполеона деньги на повторное измерение меридиана для проверки и улучшения нашей работы:


Вычисляя секунду, мы отталкивались от продолжительности года. А килограмм в качестве единицы массы мы вывели из одного литра воды. Если какая-либо жидкость и является особенной, то это, конечно, вода. Лавуазье и я много спорили по поводу идеальной температуры. Вариантов было два: 0 °С и 4 °С. Первоначально мы думали о 0 °С, потому что лед легко увидеть. Но затем мы остановили свой выбор на 4 °С, потому что именно при такой температуре вода достигает максимальной плотности. Переход к 4 °C был предложен Луи Лефевром-Жане. Объем литра мы определили как куб одной десятой метра. После сравнения с высокоточными измерениями дистиллированной воды 1 кг оказался равным 1.000028 дм3 воды. Заинтересованный читатель может найти намного более подробную информацию о процессе проведения измерений воды и о создании исходной метрической системы. Более краткую историю на английском языке можно найти в недавней книге Уильямса.
Не хочу хвастаться, но мы также придумали само название «метр» (происходящее от греческого metron и латинского metrum), которое мы и предложили 11 июля 1792 года в качестве названия для новой единицы длины.
Чтобы соблюсти историческую точность, хочу отметить: пока я не вошел в небесные сферы, я всегда думал, что наша группа первой осуществила подобное. Я был поражен, когда вскоре после моего прибытия Я-син и Нанкин Юэ рассказали мне о своей экспедиции по определению единицы измерения длины, проходившей с 721 по 725 г., то есть более чем за 1000 лет до нашей.
Я очень рад, что мы определили метр таким образом. Первоначально идея состояла в том, чтобы определить метр с помощью маятника правильной длины с полупериодом в 1 секунду. Но я не хотел, чтобы какие-либо изменения, связанные с секундой, повлияли на длину метра. Так как определенного рода зависимости в системе единиц неизбежны, они должны быть сведены к минимуму.
В то время идея определять метр, основываясь на форме Земли, а секунду — на движении Земли вокруг Солнца, казалась хорошей. Это была даже лучшая идея, которую мы могли реализовать в то время. Мы не знали, как приливы и время изменили форму Земли, или как материки отдалялись друг от друга. Но мы верили в будущее человечества, верили в то, что точность измерений будет возрастать, хотя и не знали, что конкретно изменится. Это были первые наши шаги, предпринятые для точного измерения расстояний во Франции. На сегодняшний день у нас есть высокоточные геокарты:

Лучшие мастера моего времени плавили платину, и мы ковали бруски длиной в метр и образцы килограмма. Это было захватывающее время. Два раза в неделю я останавливался у Марка-Этьена Жанета — там, где он выковывал наши первые образцы килограмма. Плавление платины и придание ей формы не было еще отработано. Жанет — ювелир Людовика XVI — был настоящим мастером в работе с платиной (если быть совсем точным, с платиновыми губками). Всего за несколько лет до этого, 6 июня 1782 года, Лавуазье показал плавление платины в водородно-кислородном пламени будущему царю Павлу I; последний приезжал с визитом к Марии Антуанетте и Людовику XVI. В дальнейшем Этьен Ленуар сделал наш платиновый метр, а Жан-Николя Фортин — платиновый килограмм. Читателям, интересующимся историей платины, я рекомендую книгу Макдональдса и Ханта.
Платина — особый металл: для нее характерны высокая плотность и химическая инертность. Кроме того, она не такая мягкая, как золото. Лучшие на сегодняшний день эталоны килограмма сделаны из платино-иридиевого сплава (добавление иридия к платине действительно улучшает его механические свойства). Ниже приведено сравнение некоторых физических характеристик платины, золота и иридия:

Это звучит просто, но в то время лучшие ученые провели бесчисленное количество часов в расчетах и экспериментах, чтобы найти лучшие материалы, лучшие формы и наилучшие условия для определения новых единиц. Но и новый образец метра, и новый килограммовый цилиндр были макроскопическими телами. Все макроскопические артефакты трудно транспортировать (мы разработали специальные футляры для перевозки); они изменяются совсем немного даже спустя 100 лет использования, абсорбции и десорбции, нагревания и охлаждения. В результате технического прогресса девятнадцатого и двадцатого веков стало возможным измерять время, массу и длину с точностью до одной миллиардной. А измерение времени может быть сделано в миллиард раз лучше.
Я до сих пор очень хорошо помню, что после того, как мы сделали новые эталоны длины и массы, Лавуазье сказал:»ничего более величественного и простого не выходило из рук человека». Я и сейчас так думаю.
Наша цель состояла в том, чтобы создать единицы измерения, удобные для всех. Наш девиз звучал как: «для всех народов — во все времена». Мы разместили копии метра по всему Парижу, чтобы все знали, какой именно длины он был (в следующий раз, когда вы посетите Париж, не забудьте посмотреть на mètre étalon рядом с Люксембургским дворцом). Вот на этой фотографии, которую я недавно нашел, показано, как заинтересованно немецкий турист изучает историю одного из немногих оставшихся эталонов метра:

Это было захватывающее время (пускай даже меня не было рядом, когда комиссия завершила эту работу). Наши единицы измерения использовались в большинстве европейских стран в девятнадцатом и большей части двадцатого века. Мы создали метр, секунду и килограмм. Позже к результатам нашей работы были прибавлены еще четыре основные величины (ампер, кандела, моль и кельвин). С этими обновлениями метрическая система прослужила человечеству более двухсот лет.
На графике ниже изображен резкий взлет частоты использования в книгах слов килограмм, километр и килогерц, случившийся после Метрической конвенции 1875 года:

Мы определили только метр, секунду, литр и килограмм. Сегодня в СИ входит гораздо больше единиц: беккерель, кулон, фарад, грэй, генри, герц, джоуль, катал, люмен, люкс, ньютон, ом, паскаль, сименс, зиверт, тесла, вольт, ватт и вебер. Вот список размерных соотношений (никакого физического смысла не подразумевается) между производными единицами:


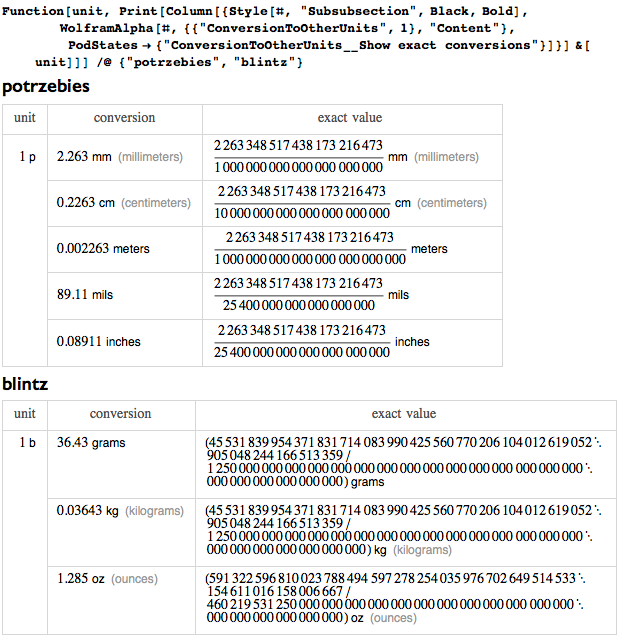
Многие именные единицы, добавленные уже после моей смерти, были связаны преимущественно с электрическими и магнитными явлениями, которые еще не были известны при моей жизни. И хотя я в целом серьезный человек, я люблю шутки и каламбуры. Однако мне не по душе, когда шутят над единицами измерения. Например, существует такая система с единицами измерения: potrzebie, ngogn, blintz, whatmeworry, cowznofski, vreeble, hoo и hah (система введенная Дональдом Кнутом (Knuth’s Potrzebie system of units)). Мало того, что их имена бессмысленны, — их значения так же не имеют смысла:
Или посмотрите на предложение Макса Петерсона касательно единиц измерения для биологии. Названия единиц и префиксы могут показаться смешными, но для меня единицы измерения — слишком серьезный предмет:

Эти названия единиц даже не рифмуются ни с одним из имен собственных:


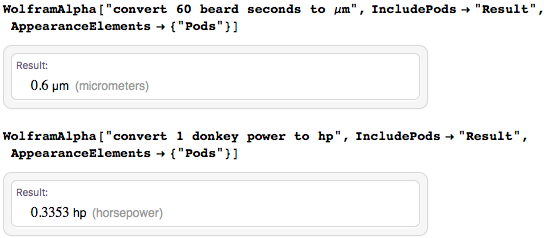
Повторюсь: я люблю иногда пошутить (даже с единицами измерения), но должно быть ясно, что это не всерьез:
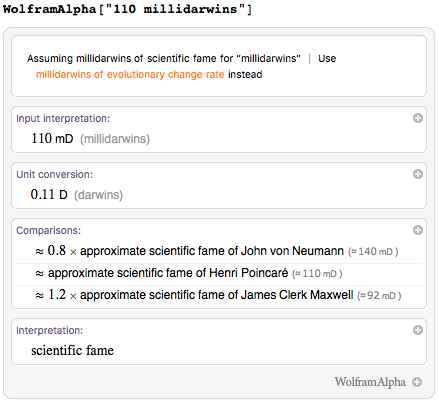
Есть еще явно ненаучные единицы, — такие, как «helens» для красоты, «puppies» для счастья или «darwins» — для славы:


Я очень горжусь тем, что единицы СИ — это не мертвые бумажные символы, а инструменты, которые регулируют современный мир. Хотя я и не любитель комиксов, мне понравилось недавнее представление базовых единиц измерения в виде супергероев от Национального института стандартов и технологий (NIST):

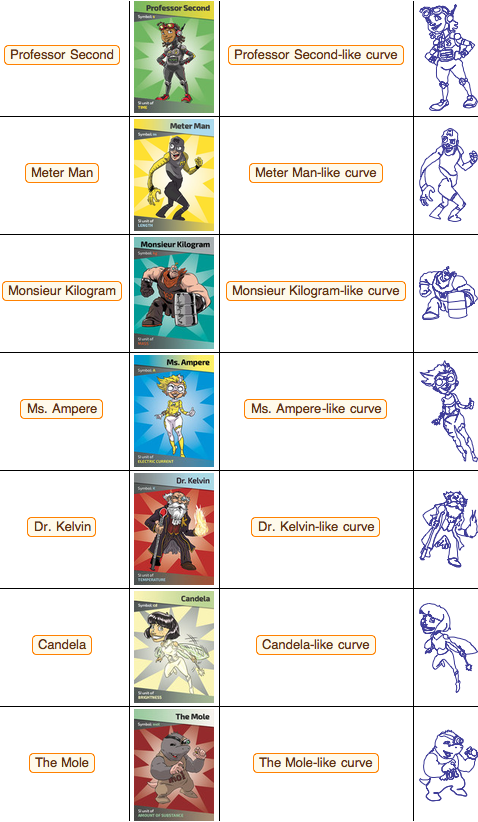
Обратите внимание: чтобы почтить вклад пяти великих математиков в создание метрической системы, кривые в крайнем правом столбце даются в виде математических формул; например, для д-ра Кельвина у нас имеется следующая чисто тригонометрическая параметризация:

Таким образом, мы можем «построить» доктора Кельвина:
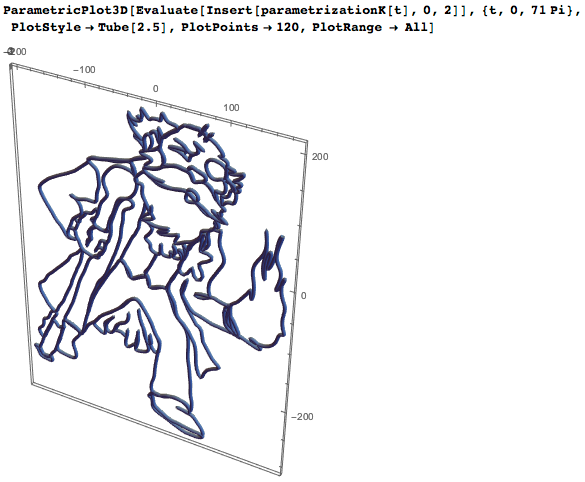
Наличие таких персонажей в параметрической форме — это очень удобно: когда моя семья собирается вместе, малыши занимаются своим любимым делом: раскрашивают супергероев. Я просто распечатываю кривые, а затем дети могут развлекаться (я позаимствовал эту идею пару лет назад из раскраски от NCSA).

И всякий раз, когда выходит новый эпизод, все собираются вместе, чтобы посмотреть его. Как вы понимаете, последний эпизод — наш любимый. Ходят слухи, что предстоящая книга Возвращение метрологов (2018 — станет идеальным годом!) дополняет существующую книгу.
Я рад, что важность измерений и основной метрической системы отмечается на Всемирном дне метрологии — 20 мая.
В то время, когда я жил, люди измеряли только товары: зерно, картофель и другие продукты, а также вино, ткани, дрова и т.д. Так что моей стране действительно нужны были единицы длины, площади, объема, и, конечно, единицы времени. Я всегда знал, что важность измерений будет со временем только расти. Весьма примечательно, что только спустя 200 лет после того, как я вошел в небесные сферы, число измеряемых физических величин достигло нескольких сотен. На сегодняшний день только Международная организация стандартизации (ISO) определяет и описывает, какие физические величины следует использовать. Ниже приводится изображение интерактивной демонстрации (загрузите документ вверху этого поста, чтобы взаимодействовать с ним), на котором графически показаны размерности физических величин для подмножеств выбранных единиц измерения. Сначала выберите два или три измерения (основные единицы измерения). Затем на графике будут показаны сферы с размерами, пропорциональными количеству различных единиц измерения, которые получаются из выбранных. Например, в случае с «метром», «секундой» и «килограммом» диаграмма показывает такие единицы измерения физических величин, как импульс (кг1 м1 с-1) или энергию (кг2 м1 с-2):
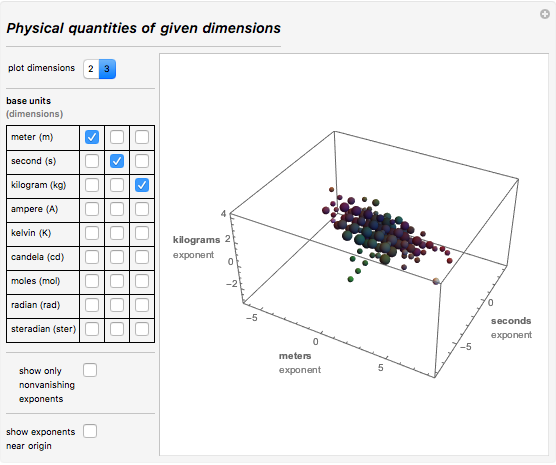
Вот отрывок кода, который я использовал для создания этих графиков. Это все физические величины с размерностями L2 M1 T-1. Последняя из них является слегка экзотической единицей из электродинамики 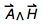 :
:

На сегодняшний день с помощью смартфонов обычные люди замеряют множество физических величин. Я бы сказал, «измерения рулят». Или как мой дорогой друг Уильям Томсон любил говорить:
… Когда вы можете измерить то, о чем вы говорите, и выразить это в цифрах, — вы знаете что-то об этом;, но когда вы не можете выразить это в цифрах, ваши знания скудны и неудовлетворительны; это может быть начало знания, но, независимо от предмета, вы вряд ли добрались до стадии науки.
Вот графическая визуализация физических величин, которые измеряются с помощью наиболее распространенных измерительных приборов:

Электрические и магнитные явления только набирают популярность. Электромагнитные эффекты, связанные с физическими величинами, стали популярными гораздо позже:

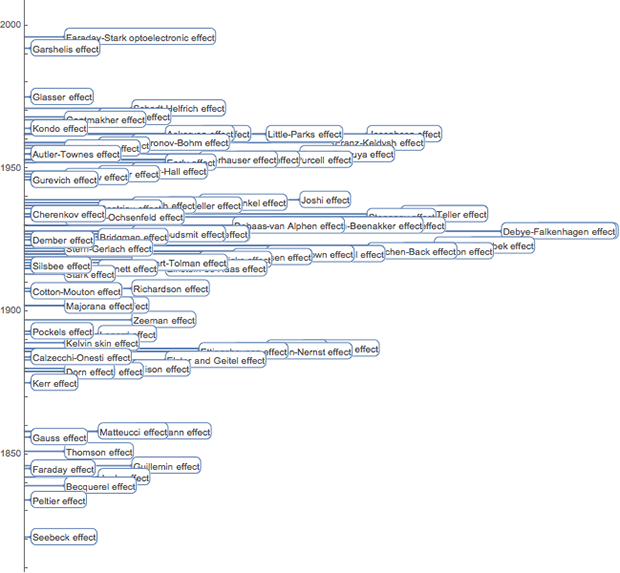
До сих помню, как я был взволнован, когда во второй половине ХIХ века и в начале ХХ века были обнаружены различные физические величины электромагнетизма и поняты их взаимосвязи (и не забудьте про недавнее добавление мемристора). Ниже представлена диаграмма, демонстрирующая наиболее важные электрические/магнитные физические величины qk, которые имеют отношения вида qk = qi qj:

С другой стороны, я был уверен, что явления, связанные с температурой, вскоре будут поняты в полной мере. И действительно: всего 25 лет спустя Карно доказал, что теплота и механическая работа эквивалентны. Теперь я также знаю о замедлении времени и сокращении длины в соответствии с теорией Эйнштейна. Однако человечеству до сих неизвестно, является ли движущееся тело более холодным или более теплым, чем неподвижное (или они имеют одинаковую температуру). Каждую неделю я слышу от Уилларда Гиббса о смежной теме отрицательных температур. А в последнее время он был очень взволнован новостью о том, что значение максимальной температуры для данного объема V выражается через фундаментальные константы:

Максимальная температура одного кубического сантиметра:

Увеличение числа констант
Спустя продолжительное время после моей физической смерти лучшие ученые в области физики 19-го и начала 20-го вв. — Джеймс Максвелл, Джордж Стони и Макс Планк (и Гилберт Льюис) обсуждали единицы измерения времени, длины и массы, основанные на неизменных свойствах микрочастиц и связанных с фундаментальными физическими константами (скорость света, гравитационная постоянная, заряд электрона, постоянная Планка и т.д.):
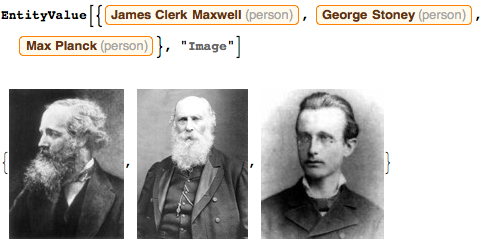
Максвелл писал в 1870 году:
Тем не менее, размеры нашей Земли и время ее вращения характеризуются завидным постоянством. Земля может сжиматься, охлаждаясь, или расширяться за счет слоя метеоритов, падающих на нее, или скорость ее вращения может ослабиться, — и все же она будет такой же планетой, как и раньше.Но молекула, скажем, водорода, если ее масса или время ее вибрации изменятся хотя бы немного, больше не будет молекулой водорода.
Итак, если мы хотим получить стандарты длины, времени и массы, которые должны быть абсолютно постоянными, мы должны искать их не в размерах, или движении, или массе нашей планеты, но в длине волны, периоде вибрации и в абсолютной массе этих нетленных, неизменных и совершенно подобных молекул.
Когда мы видим, что здесь, как и в звездном небе, присутствует неисчислимое множество маленьких тел одинаковой массы, не разделяющихся дальше и вибрирующих одновременно мно
