[Перевод] Почему алгоритмы так ML трудно настраивать?20.02.2021 17:48

В машинном обучении линейные комбинации функций потерь встречаются повсюду. На самом деле, они обычно используются в качестве стандартного подхода, несмотря на то, что это опасная область, полная подводных камней. Особенно в отношении того, как линейные комбинации затрудняют настройку алгоритма.

Возможно, вы уже знаете всё, что мы хотим сказать. Однако у нас сложилось впечатление, что в большинстве учебных программ по машинному обучению не очень хорошо обсуждаются методы оптимизации и, следовательно, градиентный спуск рассматривается как единственный метод решения всех проблем. И главный посыл состоит в том, что, если алгоритм не работает для вашей проблемы, вам нужно потратить больше времени на настройку гиперпараметров. Поэтому мы надеемся, что эта статья поможет устранить некоторую путаницу в том, как решить проблему фундаментальным и принципиальным способом. И, может быть, это поможет вам тратить меньше времени на настройку алгоритмов и больше времени на исследование.

В этом посте мы надеемся изложить следующие аргументы:

• Многие проблемы в машинном обучении следует рассматривать как многоцелевые, а в настоящее время это не так.
• Отсутствие многоцелевого подхода приводит к трудностям настройки гиперпараметров для алгоритмов машинного обучения.
• Практически невозможно обнаружить, когда возникают проблемы, поэтому их сложно обойти.
• Есть методы решения этой проблемы, которые могут быть немного сложными, но не требуют большего, чем несколько строк кода.

Линейные комбинации потерь повсюду

В то время как существуют проблемы с одной целью, эти цели обычно получают дополнительную регуляризацию. Мы выбрали несколько таких целей оптимизации со всей области машинного обучения.

Во-первых, у нас есть регуляризаторы, снижение веса и LASSO. Очевидно, что когда вы добавляете эти регуляризации, вы фактически создаёте многоцелевую потерю для вашей проблемы. В конце концов, что вас действительно волнует, так это то, как исходные потери L0 и регуляризованные потери остаются низкими. И вы настроите баланс между ними с помощью параметра λ.

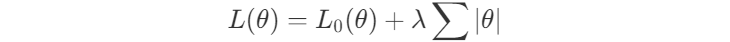
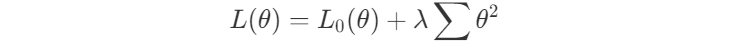
Как следствие, потери, обнаруженные, например, в VAE, фактически являются многоцелевыми, причём первая цель состоит в том, чтобы максимально охватить данные, а вторая — оставаться близким к предыдущему распределению. В этом случае иногда для введения настраиваемого параметра β используется подход KL anneling, чтобы помочь справиться с многоцелевым характером этой потери.

Кроме того, вы можете увидеть такое множество целей в обучении с подкреплением. Мало того, что во многих средах принято просто суммировать очки, полученные за достижение частичных целей. Функции потерь обычно также представляют собой линейную комбинацию потерь. Возьмём в качестве примера потери в PPO, SAC и MPO, энтропийно регуляризованных методов с их перестраиваемым параметром α.

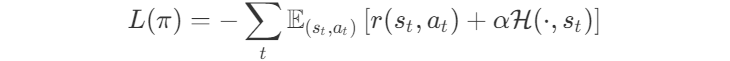
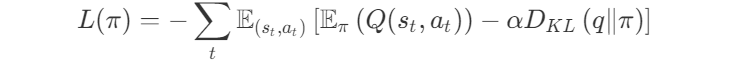
Наконец, GAN-потери — сумма между дискриминатором и потерями генератора:

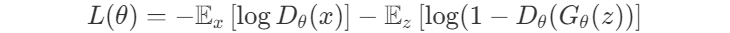
Все эти потери имеют что-то общее, они эффективно пытаются оптимизировать для нескольких целей одновременно и утверждают, что оптимум находится в уравновешивании этих часто противоречащих сил. В некоторых случаях сумма является более подходящими конкретному случаю, и для взвешивания частей друг против друга вводится гиперпараметр. В некоторых случаях существуют чёткие теоретические основы того, почему потери объединяются таким образом, и никакой гиперпараметр не используется для настройки баланса между частями.

В этой статье мы надеемся показать вам, что такой подход к объединению потерь может показаться привлекательным, но эта линейная комбинация на самом деле ненадёжна и коварна. Балансировка часто похожа на хождение по канату.

Наш маленький пример

Рассмотрим простой случай, когда мы пытаемся оптимизировать такую линейную комбинацию потерь. Мы используем подход оптимизации общих потерь, который представляет собой сумму потерь. Мы оптимизируем комбинацию с помощью градиентного спуска и наблюдаем следующее поведение.
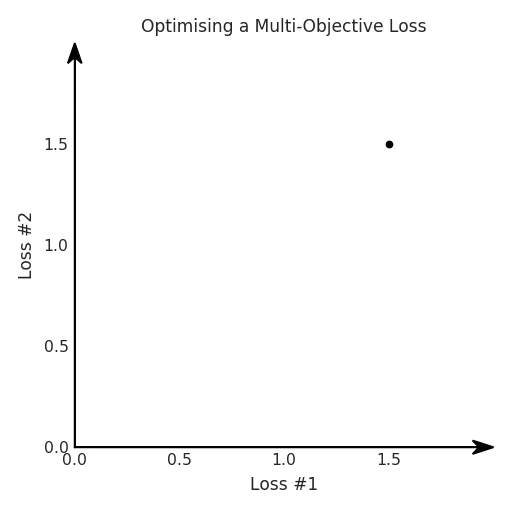
Наш код в Jax будет выглядеть примерно так:

def loss(θ):
  return loss_1(θ) + loss_2(θ)
loss_derivative = grad(loss)
for gradient_step in range(200):
  gradient = loss_derivative(θ)
  θ = θ - 0.02 * gradient

Как это обычно бывает, мы не обрадовались компромиссу между двумя потерями сразу. Поэтому ввели масштабирующий коэффициент α для второй потери и запускаем следующий код:

def loss(θ, α):
  return loss_1(θ) + α*loss_2(θ)
loss_derivative = grad(loss)
for gradient_step in range(200):
  gradient = loss_derivative(θ, α=0.5)
  θ = θ - 0.02 * gradient

Поведение, которое мы надеемся увидеть, заключается в том, что при настройке этого α мы можем выбрать компромисс между двумя потерями и выбрать точку, которая нас больше всего устраивает для нашего приложения. Мы фактически перейдём к циклу настройки гиперпараметров, вручную выберем α, запустим процесс оптимизации, решим, что мы хотели бы, чтобы вторая потеря была ниже, соответственно настроим наш α и повторим весь процесс оптимизации. После нескольких итераций мы останавливаемся на найденном решении и продолжаем писать статьи.

Однако это происходит не всегда. Фактическое поведение, которое мы иногда наблюдаем для нашей проблемы, выглядит следующим образом.

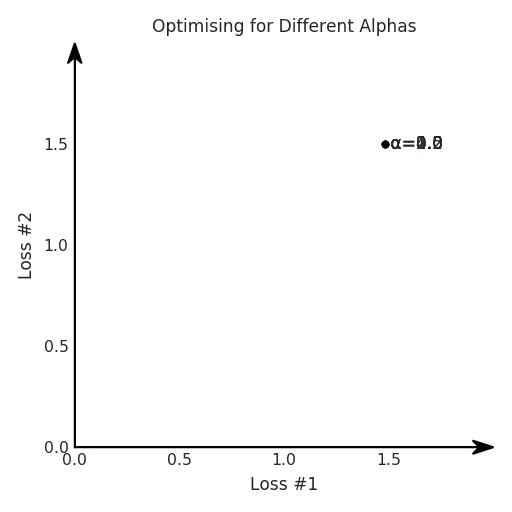
Похоже, что независимо от того, как мы точно настроим наш α-параметр, мы не сможем найти хороший компромисс между нашими двумя потерями

Мы видим два кластера решений: один, где игнорируется первая потеря, и другой, где игнорируется вторая потеря. Однако оба эти решения не полезны для большинства приложений. В большинстве случаев более предпочтительным решением является точка, в которой две потери были более сбалансированы.

На самом деле, эта диаграмма двух потерь в ходе обучения почти никогда не строится, поэтому динамика, показанная на этом рисунке, часто остаётся незамеченной. Мы просто смотрим на кривую обучения, изображающую общую потерю, и можем сделать вывод, что этот гиперпараметр нуждается в дополнительной настройке времени, поскольку он кажется по-настоящему чувствительным. В качестве альтернативы мы могли бы согласиться на подход ранней остановки обучения, чтобы цифры в документах работали. В конце концов, рецензенты любят эффективность данных.

Но где же всё пошло не так? Почему этот метод то работает, то не даёт вам настраиваемый параметр? Для этого нам нужно глубже изучить разницу между этими двумя фигурами.

Обе цифры генерируются для одной и той же задачи, используя одни и те же потери, и оптимизируют эти потери с помощью одного и того же метода оптимизации. Так что ни один из этих аспектов не виноват в разнице. То, что изменилось между этими проблемами, — это модель. Другими словами, влияние параметров модели θ на результат модели различен.

Поэтому давайте создадим и визуализируем то, что обычно не визуализируется, фронт Парето для обеих наших оптимизаций. Это совокупность всех решений, достижимых нашей моделью, в которой не доминирует ни одно, ни другое решение. Другими словами, это набор достижимых потерь, где нет такой точки, в которой все потери лучше. Независимо от того, как вы выбираете компромисс между двумя потерями, предпочтительное решение всегда лежит на фронте Парето. Настраивая гиперпараметр вашей потери, вы обычно надеетесь просто найти другую точку на том же фронте.

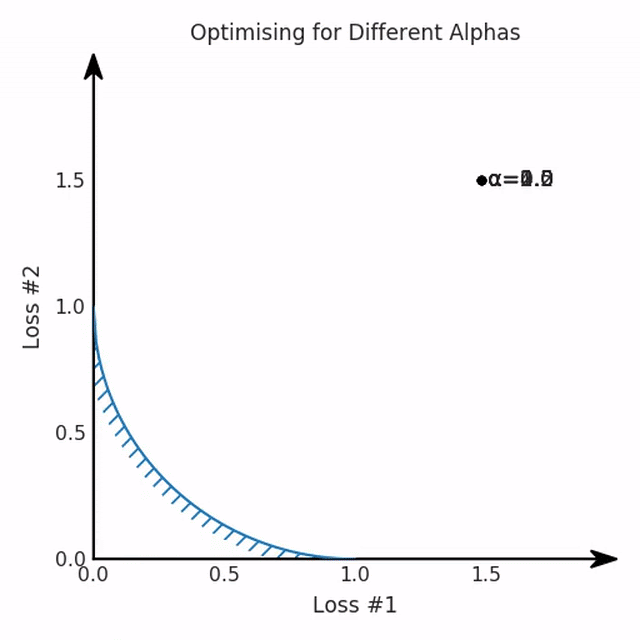
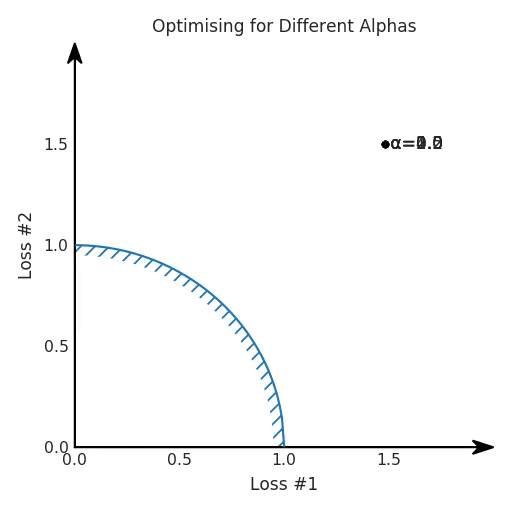
Разница между двумя фронтами Парето — это то, что заставляет настройку хорошо работать в первом случае и ужасно ошибаться после изменения нашей модели. Оказывается, когда фронт Парето выпуклый, мы можем достичь всех возможных компромиссов, настроив наш α-параметр. Однако, когда фронт Парето вогнут, этот подход не работает хорошо.

Почему не удаётся оптимизировать градиентный спуск для вогнутых фронтов Парето?

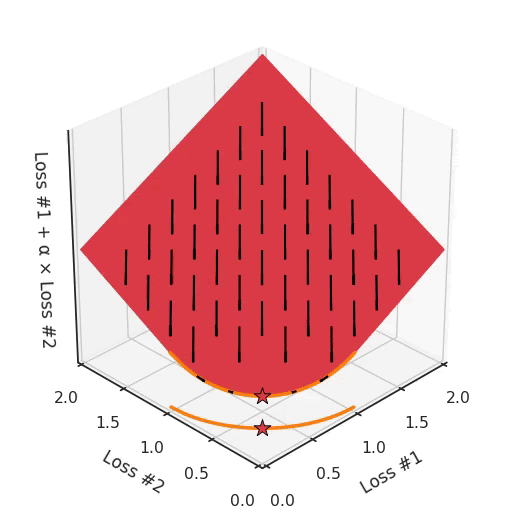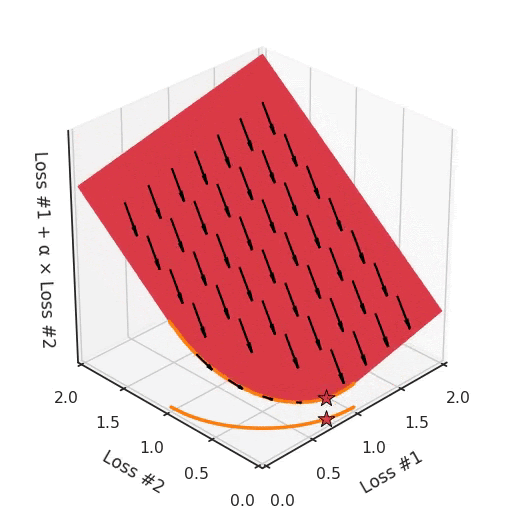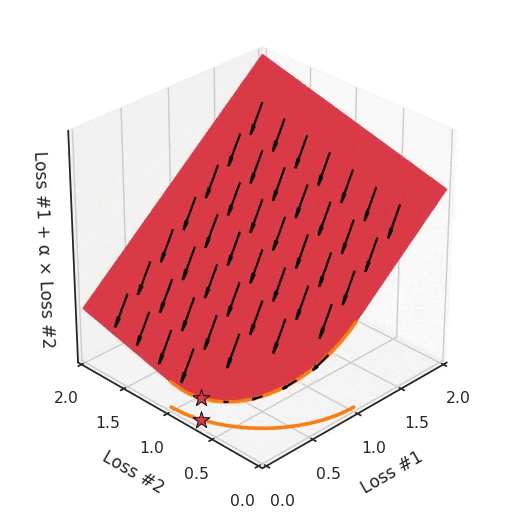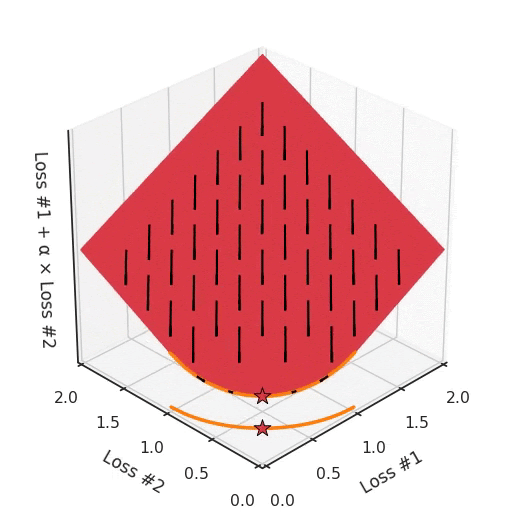
Мы можем проиллюстрировать, почему это так, посмотрев на общую потерю в третьем измерении, потерю, которая фактически оптимизируется с помощью градиентного спуска. На следующем рисунке мы визуализируем плоскость полной потери по отношению к каждой из потерь. В то время как мы фактически спускаемся на эту плоскость, используя градиент относительно параметров, каждый шаг градиентного спуска, который мы делаем, также обязательно будет идти вниз на этой плоскости. Вы можете представить себе процесс оптимизации градиентного спуска как установку сферического камешка на эту плоскость, позволяя ему колебаться под действием силы тяжести, и ждать, пока он не остановится.

Точки, где процесс оптимизации останавливается, являются результатом процесса оптимизации, обозначенного здесь звёздочкой. Как вы можете видеть на следующем рисунке, независимо от того, как вы раскачиваетесь по плоскости, вы всегда будете в оптимальном положении.

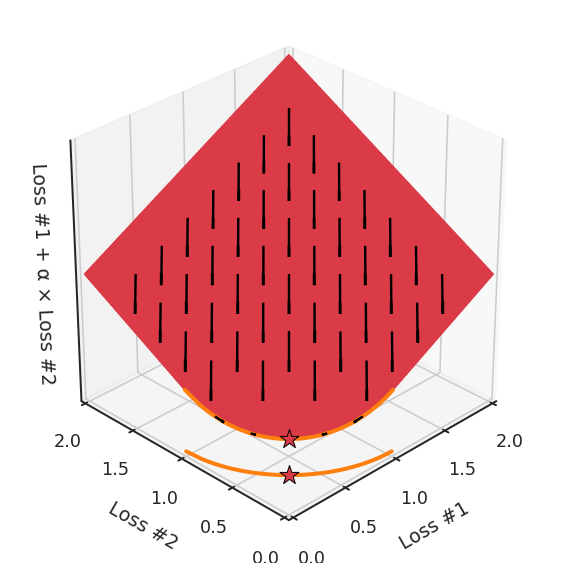
Настраивая α, это пространство остаётся плоскостью. Ведь, изменяя α, мы меняем только наклон этой плоскости. Как видите, в выпуклом случае любое решение на кривой Парето может быть достигнуто настройкой α. Чуть больше α тянет звезду влево, чуть меньше α толкает звезду вправо. Каждая начальная точка процесса оптимизации будет сходиться к одному и тому же решению, и это верно для всех значений α.
Однако, если мы посмотрим на проблему с вогнутым фронтом Парето, смоделированную по-другому, станет очевидно, откуда взялась наша проблема.
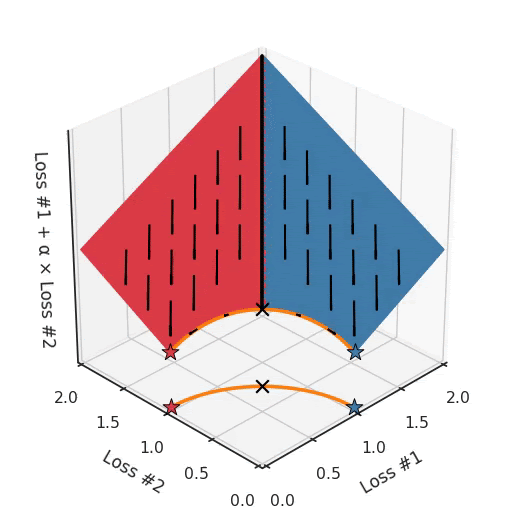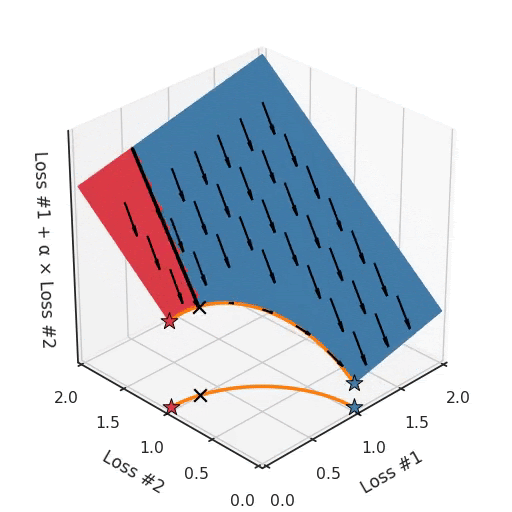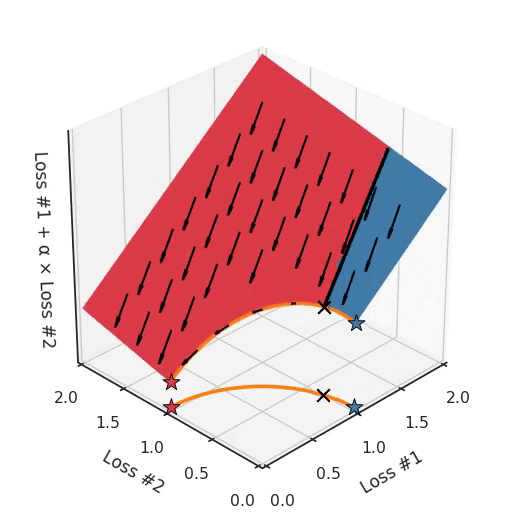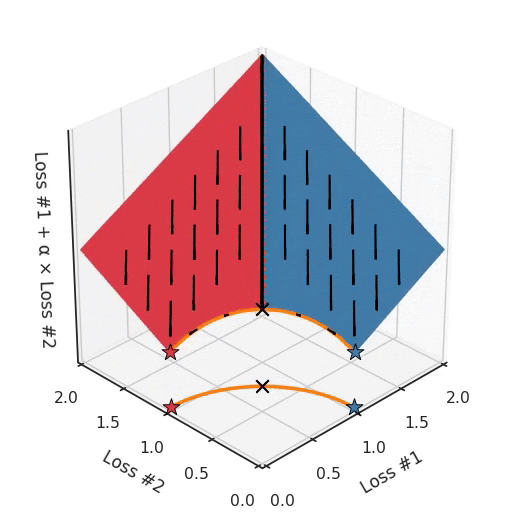
Если мы представим себе, что наш камешек следует градиентам на этой плоскости: иногда он катится больше влево, иногда больше вправо, но всегда катится вниз. Тогда ясно, что он окажется в одной из двух угловых точек — либо красной, либо синей. Когда мы настраиваем α, наша плоскость наклоняется точно так же, как и в выпуклом случае, но из-за формы фронта Парето только две точки на этом фронте будут когда-либо достигнуты, а именно точки на концах вогнутой кривой. Точка × на кривой, которую вы действительно хотели бы достичь, не может быть найдена с помощью методов, основанных на градиентном спуске. Почему? Потому что это седловая точка.

Также важно отметить, что происходит, когда мы настраиваем α. Мы можем наблюдать, что мы настраиваем, сколько из исходных точек в конечном счёте в одном решении против другого, но мы не можем настраивать так, чтобы найти другие решения на фронте Парето.

Какие проблемы вызывают эти линейные комбинации?

В заключение этой статьи мы хотели бы перечислить проблемы, связанные с использованием этого подхода с линейной комбинацией потерь:

• Во-первых, даже если вы не вводите гиперпараметр для взвешивания между потерями, неправильно говорить, что градиентный спуск будет пытаться сбалансировать противодействующие силы. В зависимости от решений, достижимых с помощью вашей модели, она вполне может полностью игнорировать одну из потерь, чтобы сосредоточиться на другой, или, наоборот, в зависимости от того, где вы инициализировали модель.
• Во-вторых, даже когда вводится гиперпараметр, он настраивается методом проб и ошибок. Вы запускаете полный процесс оптимизации, решаете, довольны ли вы, а затем настраиваете свой гиперпараметр. Вы повторяете этот цикл оптимизации, пока не будете довольны производительностью. Это расточительный и трудоёмкий подход, обычно включающий несколько итераций бегового градиентного спуска.
• В-третьих, гиперпараметр не может настраиваться на все оптимумы. Независимо от того, насколько хорошо вы настраиваете гиперпараметры, вы не найдёте промежуточных решений, которые могут вас заинтересовать. Не потому, что они не существуют, а они наверняка существуют, а потому, что был выбран плохой подход для объединения этих потерь.
• В-четвёртых, важно подчеркнуть, что для практических приложений всегда неизвестно, является ли фронт Парето выпуклым и, следовательно, можно ли настраивать эти веса потерь. Являются ли они хорошими гиперпараметрами, зависит от того, как параметризована ваша модель и как это влияет на кривую Парето. Однако визуализировать или анализировать кривую Парето для какого-либо практического применения невозможно. Визуализировать это значительно сложнее, чем нашу первоначальную задачу оптимизации. Так что, если возникнет проблема, она останется незамеченной.
• Наконец, если вы действительно хотите использовать эти линейные веса для поиска компромиссов, вам нужно явное доказательство того, что вся кривая Парето является выпуклой для конкретной используемой модели. Поэтому использования выпуклых потерь по сравнению с выходными данными вашей модели недостаточно, чтобы избежать проблемы. Если ваше пространство параметризации велико, что всегда имеет место, если ваша оптимизация включает веса внутри нейронной сети, вы можете забыть о попытках такого доказательства. Важно подчеркнуть, что демонстрации выпуклости кривой Парето для этих потерь на основе некоторых промежуточных скрытых значений недостаточно, чтобы показать, что у вас есть настраиваемый параметр. Выпуклость действительно должна зависеть от пространства параметров и от того, как выглядит фронт Парето достижимых решений.

Обратите внимание, что в большинстве задач фронты Парето не являются ни выпуклыми, ни вогнутыми, а представляют собой сочетание того и другого. Это усугубляет проблему

Возьмём, к примеру, фронт Парето, где между выпуклыми частями находятся вогнутые части. Каждая вогнутая часть не только гарантирует, что ни одно из её решений не может быть найдено с помощью градиентного спуска, но также разделит пространство инициализации параметров на две части: одна будет находить решения на выпуклой части с одной стороны, а другая — находить решения только с другой. Наличие более чем одной вогнутой части на фронте Парето усугубляет проблему, как показано на рисунке ниже.
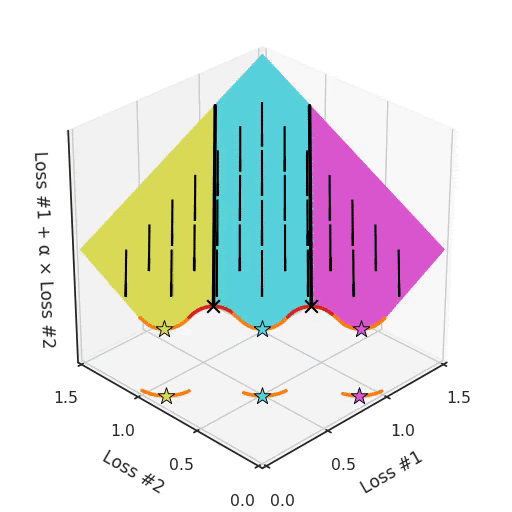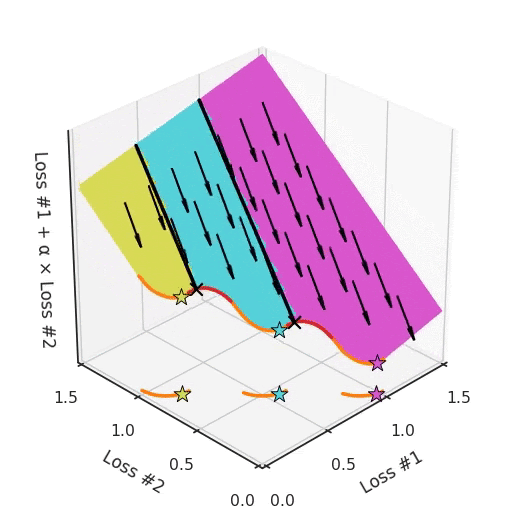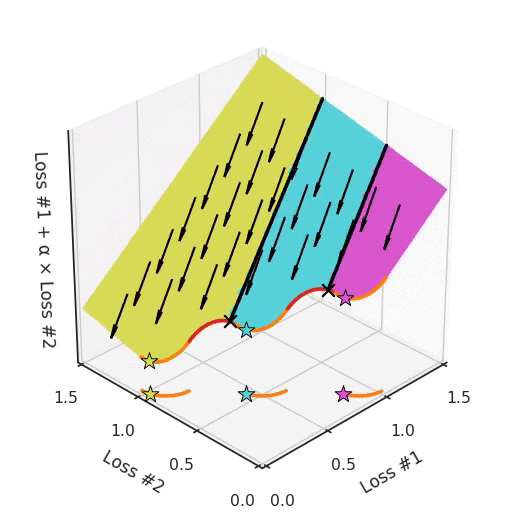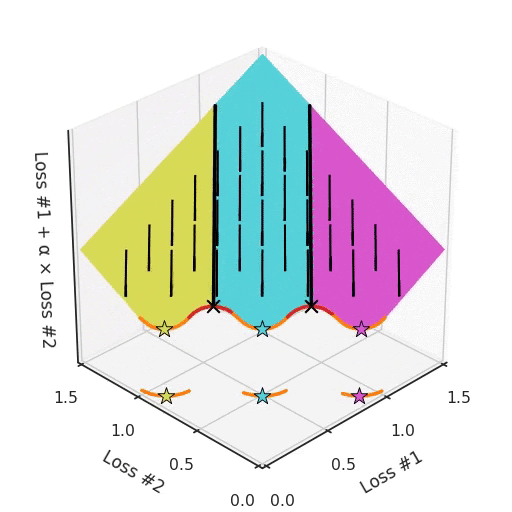
Таким образом, у нас есть не только гиперпараметр α, который не может найти все решения, в зависимости от инициализации он может найти другую выпуклую часть кривой Парето. Чтобы ещё больше усложнить работу, этот параметр и инициализация смешиваются друг с другом запутанным образом. Если вы слегка настроите свой параметр в надежде немного сместить оптимум, вы можете внезапно перейти к другой выпуклой части фронта Парето, даже если сохраните такую же инициализацию.

Все эти проблемы не обязательно должны иметь место. Есть отличные способы решения этой проблемы, способы, которые могут облегчить нашу жизнь, заставив наши оптимизации выдавать лучшие решения даже с первой попытки.

Узнайте подробности, как получить Level Up по навыкам и зарплате или востребованную профессию с нуля, пройдя онлайн-курсы SkillFactory со скидкой 40% и промокодом HABR, который даст еще +10% скидки на обучение: