[Перевод] Планеты и четвёртое измерение
Наверняка вам известно, что планеты движутся вокруг солнца по эллиптическим орбитам. Но почему? На самом деле, они двигаются по окружностям в четырёхмерном пространстве. А если спроецировать эти окружности на трёхмерное пространство, они превращаются в эллипсы.
На рисунке плоскость обозначает 2 из 3 измерений нашего пространства. Вертикальное направление — это четвёртое измерение. Планета движется по кругу в четырёхмерном пространстве, а её «тень» в трёхмерном движется по эллипсу.
Что же это за 4-е измерение? Оно похоже на время, но это не совсем время. Это такое особенное время, которое течёт со скоростью, обратно пропорциональной расстоянию между планетой и солнцем. И относительно этого времени планета двигается с постоянной скоростью по кругу в 4 измерениях. А в обычном времени его тень в трёх измерениях двигается быстрее, когда она находится ближе к солнцу.Звучит странно –, но это просто необычный способ представления обычной ньютоновской физики. Этот способ известен по крайней мере с 1980 года благодаря работе математического физика Юргена Мозера. А я узнал об этом, получив на email работу за авторством Джеспера Горансона под названием «Симметрии в задаче Кеплера» (8 марта 2015).
Самое интересное в этой работе — такой подход объясняет один интересный факт. Если взять любую эллиптическую орбиту, и повернуть её в 4-мерном пространстве, то мы получим другую допустимую орбиту.
Конечно, можно вращать эллиптическую орбиту вокруг солнца и в обычном пространстве, получая допустимую орбиту. Интересно то, что это можно делать в 4-мерном пространстве, например, заужая или расширяя эллипс.
В общем случае любую эллиптическую орбиту можно превратить в любую другую. Все орбиты с одинаковой энергией — это круговые орбиты на одной и той же сфере в 4-мерном пространстве.
Задача Кеплера
Допустим, у нас есть частица, которая двигается по закону обратных квадратов. Уравнением её движения будет

где r — позиция как функция времени, r — расстояние от центра, m — масса, а k определяет силу. Отсюда можно вывести закон сохранения энергии

для некоей константы E, зависящей от орбиты, но не меняющейся со временем. Если эта сила будет притяжением, то k > 0, а на эллиптической орбите E < 0. Будем звать частицу планетой. Планета двигается вокруг солнца, которое настолько тяжело, что его колебаниями можно пренебречь.
Будем исследовать орбиты с одной энергией E. Поэтому единицы массы, длины и времени можно принять любыми. Положим
m = 1, k = 1, E = -½
Это избавит нас от лишних букв. Теперь уравнение движения выглядит как
а закон сохранения говорит

Теперь, следуя идее Мозера, перейдём от обычного времени к новому. Назовём его s и потребуем, чтобы
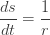
Такое время идёт медленнее по мере удаления от солнца. Поэтому скорость планеты по удалению от солнца увеличивается. Это компенсирует тенденцию планет двигаться по мере удаления от солнца более медленно в обычном времени.
Теперь перепишем закон сохранения при помощи нового времени. Поскольку для производных по обычному времени я использовал точку, давайте будем использовать штрих для производных по времени s. Тогда к примеру:

и

Используя такую производную, Горансон показывает, что сохранение энергии можно записать в виде

А это ни что иное, как уравнение четырёхмерной сферы. Доказательство будет позже. Сейчас поговорим о том, что это для нас значит. Для этого нам надо совместить меж собой координату обычного времени t и пространственные координаты (x, y, z). Точка
(t, x, y, z)
двигается в четырёхмерном пространстве по мере изменения параметра s. То есть, скорость этой точки, а именно

двигается по четырёхмерной сфере. Это сфера радиуса 1 с центром в точке
(1,0,0,0)
Дополнительные расчёты показывают другие интересные факты:

и
t''' = -(t' — 1)
Это обычные уравнения гармонического осциллятора, но с дополнительной производной. Доказательство будет позже, а пока подумаем, что это значит. Словами это можно описать так: 4-мерная скорость v совершает простые гармонические колебания вокруг точки (1,0,0,0).
Но так как v в то же время остаётся на сфере с центром в этой точки, то можно заключить, что v двигается с постоянной скоростью по кругу на этой сфере. А это подразумевает, что среднее значение пространственных компонент 4-мерной скорости равно 0, а среднее t равно 1.
Первая часть понятна: наша планета в среднем не улетает от Солнца, поэтому её средняя скорость равна нулю. Вторая часть посложнее: обычное время t движется вперёд со средней скоростью 1 относительно нового времени s, но скорость его изменения колеблется синусоидально.
Проинтегрировав обе части

мы получим

для некоего постоянного вектора a. Уравнение говорит, что позиция r гармонически осциллирует вокруг точки a. Поскольку a не меняется со временем, это сохраняющаяся величина. Это называется вектором Лапласа—Рунге—Ленца.
Часто люди начинают с закона обратных квадратов, показывают, что угловой момент и вектор Лапласа—Рунге—Ленца сохраняются, и используют эти сохраняющиеся величины и теорему Нётер, чтобы показать наличие 6-мерной группы симметрий. Для решений с отрицательной энергией это превращается в группу поворотов в 4 измерениях, SO (4). Поработав ещё немного, можно увидеть, как задача Кеплера сопряжена с гармоническим осциллятором в 4 измерениях. Это делается через репараметризацию времени.
Мне больше понравился подход Гораснона, потому что он начинается с репараметризации времени. Это позволяет эффективно показать, что эллиптическая орбита планеты — это проекция круговой орбиты в четырёхмерном пространстве на трёхмерное. Таким образом становится очевидна 4-мерная вращательная симметрия.
Горансон переносит этот подход на закон обратных квадратов в n-мерном пространстве. Получается, что эллиптические орбиты в n измерениях — это проекции круговых орбит из n+1 измерений.
Он также применяет этот подход для орбит с положительной энергией, которые представляют собой гиперболы, и для орбит с нулевой энергией (параболы). У гипербол получается симметрия групп Лоренца, а у парабол — симметрия групп Евклида. Это известный факт, однако примечательно, как просто он выводится с помощью нового подхода.
Математические детали
Из-за обилия уравнений я поставлю вокруг важных уравнений рамки. Основные уравнения — сохранение энергии, сила и изменение переменных, которые дают:

Начинаем с сохранения энергии:

затем используем

чтобы получить

Немного алгебры — и получаем

Это показывает, что 4-мерная скорость

остаётся на сфере единичного радиуса с центром в (1,0,0,0).
Следующий шаг — взять уравнение движения

и переписать его, используя штрихи (производные по s), а не точки (производные по t). Начинаем с

и дифференцируем, чтобы получить

Теперь используем другое уравнение для

и получаем

или

поэтому

Теперь хорошо бы получить формулу и для r''. Сначала посчитаем

а затем продифференцируем

Подключим формулу для r», кое-что сократится, и мы получим

Вспомним, что закон сохранения говорит

а мы знаем, что t' = r. Поэтому,

и

Получаем

Поскольку t' = r, то получается

как нам и нужно.
Теперь получим сходную формулу для r'''. Начнём с

и продиффиринцируем

Подключим формулы для r'' и r'''. Кое-что сокращается, и остаётся

Проинтегрируем обе части и получаем

для некоего постоянного вектора a. Это значит, что r гармонически осциллирует относительно a. Занятно, что и вектор r и его норма r осциллируют гармонически.
Квантовая версия планетарной орбиты — атом водорода. Всё, что мы посчитали, можно использовать и в квантовой версии. Подробности см. у Greg Egan, The ellipse and the atom.
Подробности об истории этой задачи см. у John Baez, Mysteries of the gravitational 2-body problem.
И всё это также имеет отношение к квантовой физике, суперсимметрии и йордановой алгебре!
