[Перевод] Обучение с подкреплением: практические рекомендации по обучению сетей Deep Q27.06.2022 12:46

В предыдущем материале из этой серии мы рассказали о сетях Deep Q (Deep Q Network, DQN) и написали алгоритм их обучения на псевдокоде. Хотя такие сети, в принципе, работоспособны, практическая реализация алгоритмов обучения с подкреплением (Reinforcement Learning, RL), выполняемая без понимания их ограничений, может вести к нестабильности создаваемых систем и к плохим результатам обучения. В этом материале мы обсудим два важных ограничения, две проблемы, способных привести к нестабильности Q-обучения.

9f6a54dc4c901eea8f58405192d4a17e.png

Мы поговорим и о том, как, на практике, решать эти проблемы. Вспомните о том, что уравнение Беллмана связывает, с помощью рекурсии, Q-функции для текущего и следующего временных шагов.

Уравнение Беллмана. Оптимальная Q-функция для текущего шага, отбрасывание последнего значения Q, оптимальная Q-функция для следующего шага.Уравнение Беллмана. Оптимальная Q-функция для текущего шага, отбрасывание последнего значения Q, оптимальная Q-функция для следующего шага.

DQN используют нейронные сети для приблизительной оценки Q_t и Q_{t +1}и для минимизации среднеквадратичной ошибки (Mean Squared Error, MSE) между двумя сторонами этого уравнения. Это ведёт нас к первой проблеме.

Проблема №1: ошибка Беллмана представляет собой постоянно меняющуюся величину

Ошибка Беллмана — это всего лишь MSE, вычисленная для двух сторон уравнения Беллмана. Рассмотрим формулу, используемую для вычисления среднеквадратичной ошибки:

MSE(\hat y,y)=\frac{1}{N}\sum_{i=1}^N(\hat y_i-y_i)^2.

Здесь \hat y— это прогнозируемое значение, а y— целевое значение. При решении задачи регрессии с использованием обучения с учителем, y — это фиксированное точное значение. Когда мы прогнозируем значение \hat y— нам не надо заботиться об изменении этого точного значения.

Но при применении Q-обучения формулы \hat y=Q(s_t, a_t)и y=r_t+\gamma(1-d) \max_{a} Q(s_{t+1},a_{t+1}) означают, что целевое значение y — это не точное базовое значение, а тоже спрогнозированное значение. Так как одна и та же сеть прогнозирует и значение y, и значение \hat y, это может привести к нестабильному поведению системы. При изменении Q_t меняется и прогноз для Q_{t+1}, что ведёт к появлению цикла обратной связи.

Проблема постоянно меняющейся величины при глубоком Q-обучении. Одна и та же сеть выдаёт и прогнозируемые, и целевые значения, что ведёт к появлению цикла обратной связи.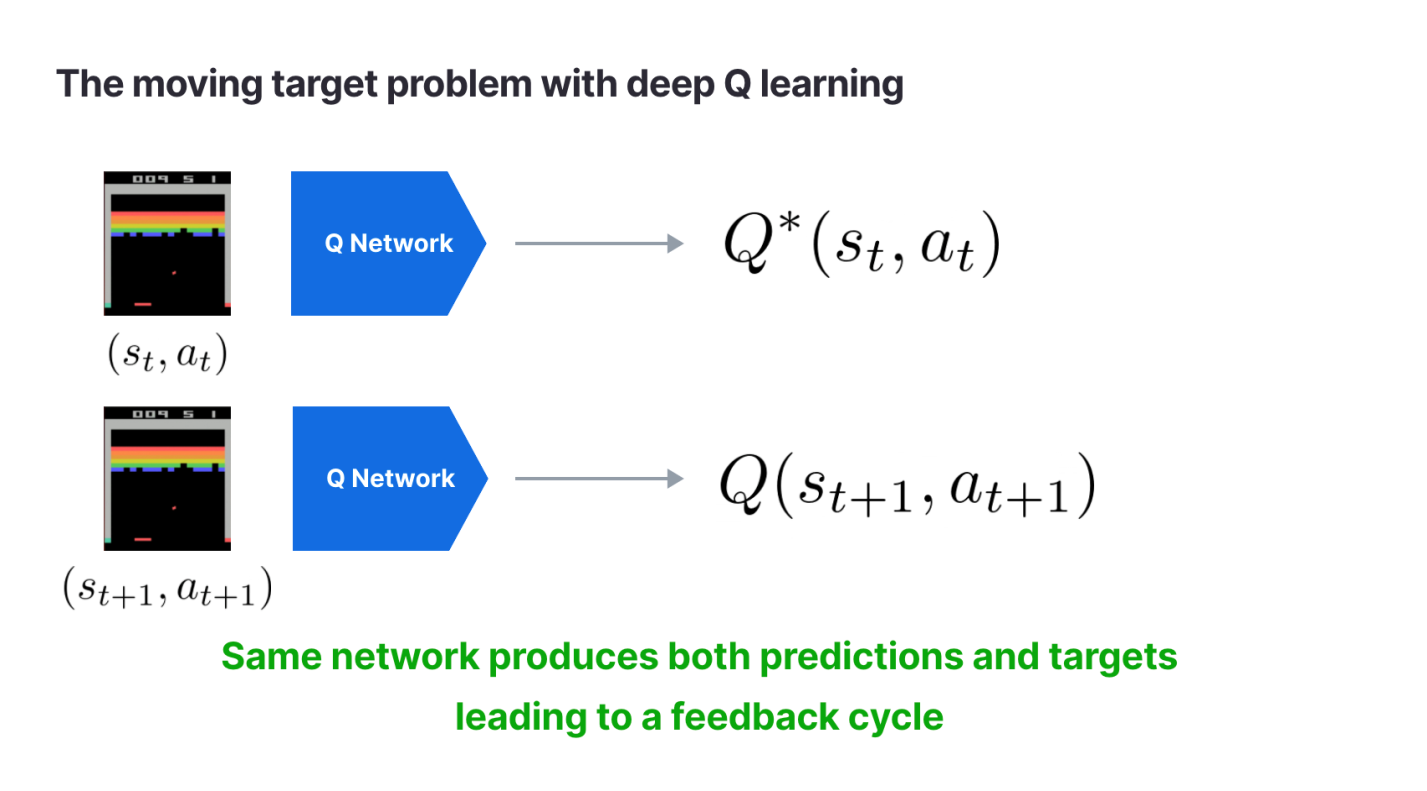Проблема постоянно меняющейся величины при глубоком Q-обучении. Одна и та же сеть выдаёт и прогнозируемые, и целевые значения, что ведёт к появлению цикла обратной связи.

Решение проблемы №1: применение для генерирования целевых значений сети, параметры которой обновляются медленнее, чем у сети, прогнозирующей обычные значения

Практическое решение этой проблемы заключается в использовании двух различных, но схожих сетей для прогнозирования значений \hat y и y. Это позволяет стабилизировать процесс обучения. В первой DQN Q-сеть используется для прогнозирования \hat y. При этом в системе хранится старая копия Q-сети, параметры которой обновляются через фиксированный интервал обучения. Эта копия сети используется для прогнозирования значения y. Это позволяет обеспечить неизменность целевых значений в течение фиксированных периодов времени. Минус этого решения заключается в том, что целевое значение в процессе обучения несколько раз внезапно изменяется.

Ещё одно решение, использованное в более поздней работе, выполненной в рамках проекта DeepMind, заключается в применении сети для прогнозирования целевых значений, веса которой представляют собой экспоненциальное скользящее среднее (Exponential Moving Average, EMA) весов сети, прогнозирующей обычные значения. EMA-веса меняются медленнее, но плавнее, чем обычные веса, что позволяет предотвратить неожиданные скачки целевых значений Q. Стратегия EMA в наши дни используется во многих эталонных RL-системах. Вот как это выглядит в коде: 

"""
Экспоненциальное скользящее среднее
"""
def target_Q_update(pred_net, target_net, beta=0.99):
	target_net.weights = beta * target_net.weights + \
												(1-beta) pred_net.weights
	return target_net

Проблема №2: Q-обучение даёт слишком оптимистичные результаты

Постоянно изменяющиеся значения — это не единственная проблема Q-обучения. Ещё одна проблема заключается в том, что прогнозы, сделанные с помощью Q-функций, оптимизированных с применением ошибки Беллмана, оказываются слишком оптимистичными. Хотя в обществе оптимизм и одобряется, слишком оптимистичные прогнозы способны довести RL-систему до состояния, когда от неё не будет никакой практической пользы. «Оптимизм», с точки зрения обучения с подкреплением, это — когда алгоритм переоценивает то, какой результат R можно получить в будущем. Если вы представляете некую компанию, полагающуюся на RL в принятии важнейших решений, это значит, что, доверяя слишком оптимистичной системе, вы рискуете нажить проблемы.

Что в Q-обучении является источником оптимизма? Как и в случае с проблемой постоянно изменяющихся значений, источником оптимизма является уравнение Беллмана. В начале обучения нейронная сеть точно не знает о том, каким будет реальное значение Q. Поэтому, когда сеть делает прогноз, для него характерна некоторая ошибка. Корень зла тут — операция max. Прогнозирование целевого значения, \max_{a} Q(s_{t+1},a_{t+1}), всегда будет приводить к выбору самого большого значения Q, даже в том случае, если это будет неправильное значение. Для того чтобы было понятнее — рассмотрим пример.

Проблема оптимизма при Q-обучении. При использовании ошибки Беллмана Q-функция будет систематически переоценивать фактическое значение.Проблема оптимизма при Q-обучении. При использовании ошибки Беллмана Q-функция будет систематически переоценивать фактическое значение.

Этот пример демонстрирует тот факт, что в ситуации неопределённости целевая Q-функция всегда будет вести себя оптимистично. Проблема заключается в систематичности этого оптимизма. Это означает, что DQN, из-за использования операции \max_{a}, будет делать больше ошибок из-за оптимистичных оценок, чем из-за пессимистичных. Эта постоянная тяга к оптимизму в процессе обучения быстро превратится в серьёзную ошибку.

Решение проблемы №2: обучать две Q-сети и использовать ту, что даёт более пессимистичные результаты

На решение этой проблемы направлен алгоритм Double Q-learning. Он реализуется путём обучения двух совершенно различных и независимых Q-функций. Для нахождения параметров сети алгоритм выбирает минимальное значение из тех, что выдают две Q-функции. Две Q-сети, используемые в такой системе, можно рассматривать как ансамбль сетей. Каждая сеть отдаёт свой голос за то значение Q_{t+1}, которое она считает правильным. Побеждает голос, отданный за самое пессимистичное значение. В принципе, можно использовать не две, а N таких сетей для того чтобы получить больше голосов, но на практике для решения проблемы оптимистичных оценок достаточно и двух сетей. Вот как выглядят вычисления при использовании алгоритма Double Q-learning: 

def compute_target_Q(target_net1, target_net2):
	target_Q = minimum(target_net1, target_net2, dim=1)
	return target_Q

При использовании этого алгоритма в системе, играющей в игры Atari, получились более консервативные результаты работы Q-функции, чем при применении обычного алгоритма DQN.

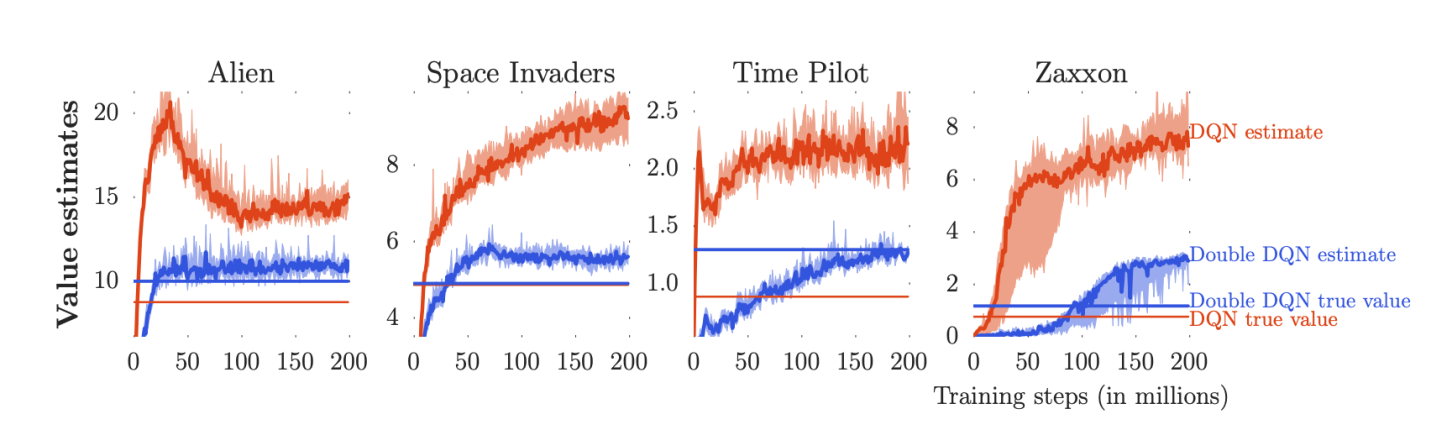Оценки значений, полученные при использовании алгоритмов DQN (красная линия) и Double DQN. Алгоритм DQN склонен к переоцениванию значений, а Double DQN даёт более консервативные оценки. Источник — https://arxiv.org/abs/1509.06461Оценки значений, полученные при использовании алгоритмов DQN (красная линия) и Double DQN. Алгоритм DQN склонен к переоцениванию значений, а Double DQN даёт более консервативные оценки. Источник — https://arxiv.org/abs/1509.06461

Итоги

Мы обсудили две проблемы обучения Q-сетей и поговорили о том, как эти проблемы можно решить. Это — лишь небольшая часть тех сложностей, с которыми можно столкнуться, обучая RL-системы. К счастью, глубокое понимание этих проблем позволяет развить интуитивное представление об RL-системах. Это помогает решать данные проблемы в системах, используемых на практике, приводя в работоспособное состояние проекты, использующие алгоритмы обучения с подкреплением.

О, а приходите к нам работать?

© Habrahabr.ru