[Перевод] Объёмное атмосферное рассеяние света29.12.2017 12:33

Если вы прожили на планете Земля достаточно долго, то наверно задавались вопросом, почему небо обычно синее, но краснеет на закате. Оптическое явление, которое стало (основной) причиной этого, называется рэлеевским рассеянием. В этой статье я расскажу, как смоделировать атмосферное рассеяние, чтобы имитировать многие визуальные эффекты, которые проявляются на планетах. Если вы хотите научиться рендерить физически точные изображения чужих планет, то этот туториал определённо стоит изучить.

GIF

Статья разбита на следующие части:

Часть 1. Объёмное атмосферное рассеяние
Часть 2. Теория атмосферного рассеяния
Часть 3. Математика рэлеевского рассеяния
Часть 4. Путешествие сквозь атмосферу
Часть 5. Атмосферный шейдер
Часть 6. Пересечение атмосферы
Часть 7. Шейдер атмосферного рассеяния

Часть 1. Объёмное атмосферное рассеяние

Введение

Воссоздать атмосферные явления так сложно потому, что небо не является непрозрачным объектом. В традиционных техниках рендеринга предполагается, что объекты — это просто пустые оболочки. Все графические вычисления производятся на поверхностях материалов и не зависят от того, что находится внутри. Это сильное упрощение позволяет очень эффективно выполнять рендеринг непрозрачных объектов. Однако свойства некоторых материалов определяются тем, что свет может проходить сквозь них. Конечный внешний вид просвечивающих объектов становится результатом взаимодействия света с их внутренней структурой. В большинстве случаев такое взаимодействие можно очень эффективно имитировать, как это можно увидеть в туториале «Быстрый шейдер для Subsurface Scattering в Unity». К сожалению, в нашем случае, если мы хотим создать убедительное небо, это не так. Вместо рендеринга только «внешней оболочки» планеты нам придётся симулировать то, что происходит с лучами света, проходящими сквозь атмосферу. Выполнение вычислений внутри объекта называется объёмным рендерингом; эту тему мы подробно рассматривали в серии статей Volumetric Rendering. В этой серии статей я рассказал о двух техниках (raymarching и знаковых функциях расстояния), которые невозможно эффективно использовать для симуляции атмосферного рассеяния. В этой статье мы познакомимся с более подходящей для рендеринга просвечивающих твёрдых объектов техникой, часто называемой единичным объёмным рассеянием.

Единичное рассеяние

В комнате без света мы ничего не увидим. Объекты становятся видимыми, только когда от них отражаются лучи света и попадают в наш глаз. В большинстве игровых движков (таких как Unity и Unreal) предполагается, что свет движется в «вакууме». Это значит, что на свет могут влиять только объекты. На самом же деле, свет всегда движется в среде. В нашем случае такой средой является вдыхаемый нами воздух. Поэтому на внешний вид объекта влияет расстояние, проходимое светом в воздухе. На поверхности Земли плотность воздуха относительно мала, её влияние настолько незначительно, что её стоит учитывать только когда свет проходит большие расстояния. Далёкие горы сливаются с небом, однако на близкие объекты атмосферное рассеяние почти не влияет.

Первым шагом в воссоздании оптического эффекта атмосферного рассеяния будет анализ того, как свет проходит через такие среды, как воздух. Как сказано выше, мы можем увидеть предмет только тогда, когда свет падает в наш глаз. В контексте 3D-графики нашим глазом является камера, используемая для рендеринга сцены. Молекулы, из которых состоит воздух вокруг нас, могут отражать проходящие через них световые лучи. Поэтому они способны менять то, как мы воспринимаем объекты. Если сильно упростить, то существует два способа, которыми молекулы могут повлиять на наше зрение.

Рассеяние наружу
Наиболее очевидный способ взаимодействия молекул со светом заключается в том, что они отражают свет, меняя его направление. Если направленный в камеру луч света отражается, то мы наблюдаем процесс рассеяния наружу.

Реальный источник света может испускать каждую секунду квадрильоны фотонов, и каждый из них с определённой вероятностью может столкнуться с молекулой воздуха. Чем плотнее среда, в которой движется свет, тем вероятнее отражение единичного фотона. Влияние рассеяния наружу также зависит от пройденного светом расстояния.

Рассеяние наружу приводит к тому, что свет постепенно становится всё более тусклым, и это свойство зависит от пройденного расстояния и плотности воздуха.

Рассеяние внутрь
Когда свет отражается частицей, то может случиться так, что он перенаправляется в камеру. Такой эффект противоположен рассеянию наружу, и логично, что он называется рассеянием внутрь.

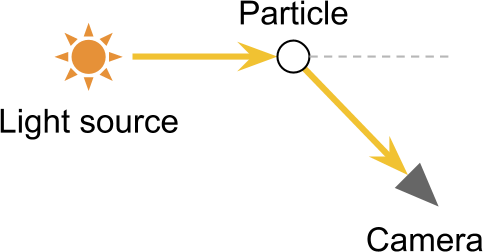
При определённых условиях рассеяние внутрь позволяет увидеть источники света, не находящиеся в прямой области видимости камеры. Наиболее очевидным результатом этого является оптический эффект — световые гало вокруг источников света. Они возникают из-за того, что камера получает из одного источника и прямые, и непрямые лучи света, что де-факто увеличивает количество получаемых фотонов.

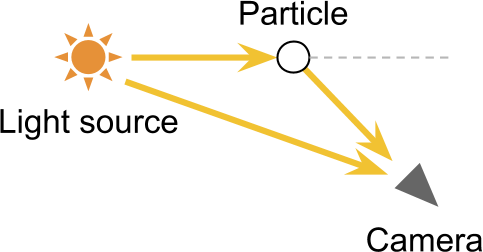
Единичное объёмное рассеяние

Один луч света может отражаться произвольное число раз. Это значит, что прежде чем попасть в камеру. луч может проходить очень сложными маршрутами. Это становится для нас серьёзной сложностью, потому что рендеринг просвечивающих материалов с высоким качеством требует симуляции путей каждого из отдельных лучей света. Эта техника называется трассировкой лучей (raytracing), и в настоящее время она слишком затратна для реализации в реальном времени. Представленная в этом туториале техника единичного рассеяния учитывает единственное событие рассеяния луча света. Позже мы увидим, что такое упрощение всё равно позволяет получать реалистичные результаты всего за небольшую долю расчётов, необходимых для настоящей трассировки лучей.

Основой рендеринга реалистичного неба является симуляция того, что происходит с лучами света при прохождении сквозь атмосферу планеты. На схеме ниже показана камера, смотрящая сквозь планету. Основная идея этой техники рендеринга заключается в вычислении того, как на прохождение света из $A$ в $B$ влияет рассеяние. Это означает, что нужно вычислить влияние, которое имеет рассеяние внутрь и наружу на луч, проходящий к камере. Как сказано выше, из-за рассеяния наружу мы наблюдаем затухание. Количество света, присутствующее в каждой точке $P \in \overline{AB}$ имеет небольшую вероятность отражения в сторону от камеры.

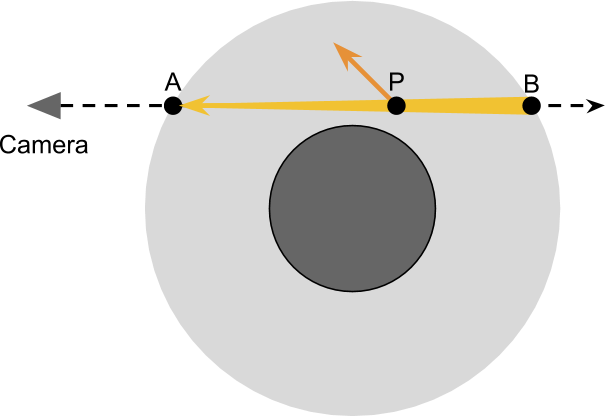
Чтобы корректно учитывать величину рассеяния наружу, происходящего в каждой точке $P$ , нам сначала нужно узнать, какое количество света присутствовало в $P$ . Если считать, что планету освещает только одна звезда, то весь свет, получаемый $P$ , должен поступать от солнца. Часть этого света будет подвержена рассеянию внутрь и отразится в камеру:

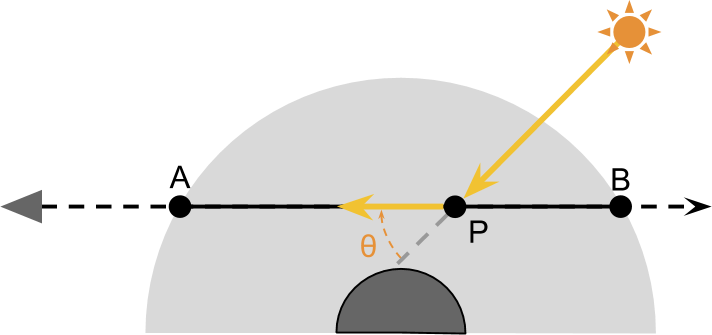
Этих двух этапов достаточно для аппроксимации большинства эффектов, наблюдаемых в атмосфере. Однако всё усложняется тем, что количество света, получаемого $P$ от солнца, тоже подвержено рассеянию наружу, когда свет проходит через атмосферу из $C$ в $P$ .

Подведём итог тому, что нам нужно сделать:

Область видимости камеры входит в атмосферу в и находится в ;
В качестве аппроксимации мы будем учитывать влияние рассеяния внутрь и наружу, когда оно происходит в каждой точке $P \in \overline{AB}$ ;
Величина света, получаемого от солнца;
Величина света, получаемого и подверженного рассеянию наружу при прохождении через атмосферу $\overline{CP}$ ;
Часть света, получаемая и подверженная рассеянию внутрь, которое перенаправляет лучи в камеру;
Часть света из , направляемая в камеру, подвергается рассеянию наружу и отражается от области видимости.

Это не единственный способ, которым лучи света могут попасть в камеру!

Предложенное в этом туториале решение учитывает рассеяние внутрь вдоль области видимости $\overline{AB}$ . Свет, достигающий точки $P$

от солнца, с определённой вероятностью может отразиться в камеру.

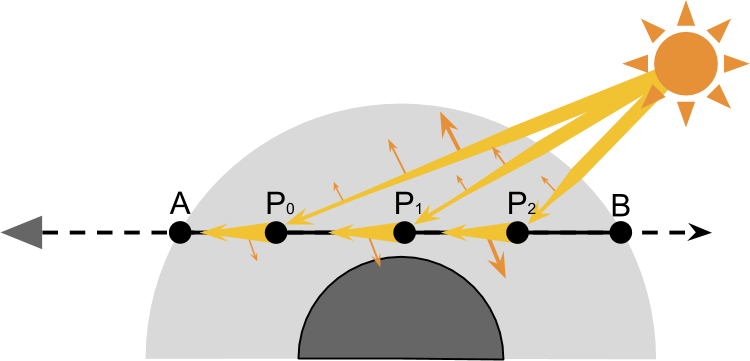
Однако существует множество путей, по которым лучи могут попасть в камеру. Например, один из лучей, рассеянный наружу на пути к $P$ , при втором столкновении может рассеяться обратно, по направлению к камере (см. схему ниже). И могут существовать лучи, достигающие камеры после трёх отражений, или даже четырёх.

Рассматриваемая нами техника называется единичным рассеянием, потому что учитывает только рассеяние внутрь, происходящее вдоль области видимости. Более сложные техники могут расширить этот процесс и учитывать другие способы, которыми луч может достичь камеры. Однако количество возможных путей растёт с увеличением количества рассматриваемых событий рассеяния экспоненциально. К счастью, вероятность попадания в камеру тоже уменьшается экспоненциально.

Часть 2. Теория атмосферного рассеяния

В этой части мы начнём выводить уравнения, управляющие этим сложным, но прекрасным оптическим явлением.

Функция пропускания

Для вычисления величины света, пропускаемого к камере, полезно совершить то же путешествие, которое проходят лучи от солнца. Посмотрев на схему ниже, легко увидеть, что лучи света, достигающие $C$ , проходят через пустое пространство. Поскольку на их пути ничего нет, весь свет достигает $C$ , не подвергаясь никакому эффекту рассеяния. Давайте обозначим переменной $I_C$ количество нерассеянного света, получаемого точкой $C$ от солнца. Во время своего путешествия к $P$ , луч входит в атмосферу планеты. Некоторые лучи сталкиваются с висящими в воздухе молекулами и отражаются в разные стороны. В результате часть света рассеивается с пути. Количество света, достигающего $P$ (обозначенное как $I_P$ ), будет меньше, чем $I_C$ .

Соотношение $I_C$ и $I_P$ называется пропусканием:

$T\left(\overline{CP}\right) = \frac{I_P}{I_C}$

Мы можем использовать его для обозначения процента света, который не был рассеян (то есть был пропущен) при путешествии от $C$ до $P$ . Позже мы исследуем природу этой функции. Пока единственное, что нам нужно знать — оно соответствует влиянию атмосферного рассеяния наружу.

Следовательно, количество света, получаемого $P$ , равно:

$I_P = I_C \, T\left(\overline{CP}\right)$

Функция рассеяния

Точка $P$ получает свет непосредственно от солнца. Однако не весь этот свет, проходящий через $P$ , передаётся обратно в камеру. Чтобы вычислить количество света, на самом деле достигающее камеры, мы введём новую концепцию: функцию рассеяния $S$ . Она будет обозначать количество света, отражённого в определённом направлении. Если мы посмотрим на схему ниже, то увидим, что к камере будут направлены только лучи, отражённые на угол $\theta$ .

Значение $S\left(\lambda, \theta, h\right)$ обозначает долю света, отражённого на $\theta$ радиан. Эта функция — основная наша проблема, и мы исследуем её природу в следующей части. Пока единственное, что нужно знать — что она зависит от цвета получаемого света (определяемого длиной волны $\lambda$ ), угла рассеяния $\theta$ и высоты $h$ точки $P$ . Высота важна потому, что плотность атмосферы изменяется как функция от высоты. А плотность является одним из факторов, определяющих количество рассеиваемого света.

Теперь у нас есть все необходимые инструменты для записи общего уравнения, показывающего количество света, переданного от $P$ к $A$ :

$I_{PA} = \boxed{I_P} \, S\left(\lambda,\theta,h\right) \, T\left(\overline{PA}\right)$

Благодаря предыдущему определению мы можем развернуть $I_P$ :

$I_{PA} = \boxed{I_C \, T\left(\overline{CP}\right)}\, S\left(\lambda,\theta,h\right) \,T\left(\overline{PA}\right)=$

$=\underset{\text{in-scattering}}{ \underbrace{I_C \,S\left(\lambda,\theta,h\right)} }\, \underset{\text{out-scattering}}{\underbrace{T\left(\overline{CP}\right)\, T\left(\overline{PA}\right)}}$

Уравнение говорит само за себя:

Свет проходит от солнца к , не рассеиваясь в вакууме космоса;
Свет входит в атмосферу и проходит от к . В этом процессе из-за рассеяния наружу только часть $T\left(\overline{CP}\right)$ достигает точки назначения;
Часть света, который добрался от солнца до , отражается назад в камеру. Доля света, подверженного рассеянию внутрь равна $S\left(\lambda,\theta,h\right)$ ;
Оставшийся свет проходит от до , и снова проспускается только часть $T\left(\overline{PA}\right)$ .

Численное интегрирование

Если вы внимательно прочитали предыдущие параграфы, то могли заметить, что яркость записывалась по-разному. Символ $I_{PA}$ обозначает количество света, переданного от $P$ к $A$ . Однако величина не учитывает весь свет, который получает $A$ . В этих упрощённых моделях атмосферного рассеяния мы учитываем рассеяние внутрь от каждой точки вдоль области видимости камеры в атмосфере.

Общее количество света, получаемого $A$ ( $I_A$ ), вычисляется сложением влияния всех точек $P \in \overline{AB}$ . С точки зрения математики, на отрезке $\overline{AB}$ есть бесконечное множество точек, поэтому циклический обход их всех невозможен. Однако мы можем разделить $\overline{AB}$ на меньшие отрезки длины $ds$ (см. схему ниже), и суммировать влияние каждого из них.

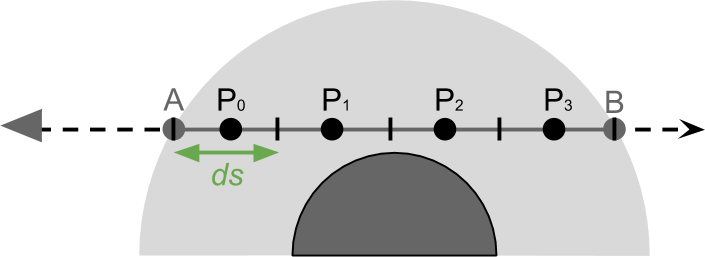
Такой процесс аппроксимации называется численным интегрированием и приводит к следующему выражению:

$I_A = \sum_{P \in \overline{AB}} {I_{PA}\, ds }$

Чем больше точек мы учитываем, тем точнее будет конечный результат. В реальности же в нашем атмосферном шейдере мы просто циклически обойдём несколько точек $P_i$ внутри атмосферы, суммируя их влияние в общий результат.

Почему мы умножаем на ds?

Здесь мы используем аппроксимацию непрерывного явления. Чем больше точек мы рассмотрим, тем ближе будем к реальному результату. Умножая каждую точку на $ds$

, мы придаём её влиянию вес согласно её длине. Чем больше точек у нас есть, тем менее важна каждая из них.

Можно посмотреть на это и иначе: умножая на $ds$ , мы «усредняем» влияние всех точек.

Направленное освещение

Если солнце относительно близко, то его лучше всего моделировать как точечный источник света. В этом случае количество полученного $C$ света зависит от расстояния до солнца. Однако если мы говорим о планетах, то часто предполагаем, что солнце находится так далеко, что его лучи падают на планету под одним углом. Если это справедливо, то мы можем моделировать солнце как направленный источник света. Свет, получаемый от направленного источника света, остаётся постоянным, вне зависимости от пройденного им расстояния. Поэтому каждая точка $C$ получает одинаковое количество света, а направление относительно солнца одинаково для всех точек.

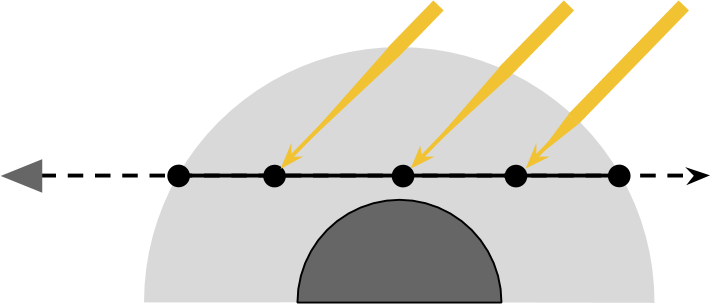
Мы можем использовать это допущение, чтобы упростить наши уравнения.

Давайте заменим $I_C$ константой $I_S$ , которая определяет яркость солнца.

$I_A = \sum_{P \in \overline{AB}} {\boxed{I_{PA}}\, ds } =$

$= \sum_{P \in \overline{AB}} {\boxed{I_C \,S\left(\lambda,\theta,h\right) \,T\left(\overline{CP}\right)\, T\left(\overline{PA}\right)}\, ds }=$

$= I_S \sum_{P \in \overline{AB}} {S\left(\lambda,\theta,h\right) \,T\left(\overline{CP}\right) \, T\left(\overline{PA}\right) \,ds }=$

Есть ещё одна оптимизация, которую мы можем выполнить, она включает в себя функцию рассеяния $S\left(\lambda,\theta,h\right)$ . Если солнечный свет всегда падает с одного направления, то угол $\theta$ становится постоянным. Ниже мы увидим, что из суммы можно исключить направленное влияние $S\left(\lambda,\theta,h\right)$ . Но пока мы его оставим.

Коэффициент поглощения

При описании возможных результатов взаимодействия между светом и молекулами воздуха, мы допустили всего два варианта — или прохождение насквозь, или отражение. Но существует и третья возможность. Некоторые химические соединения поглощают свет. В атмосфере Земли есть множество веществ, обладающих таким свойством. Озон, например, находится в верхних слоях атмосферы и активно взаимодействует с ультрафиолетовым излучением. Однако его присутствие не оказывает практически никакого воздействия на цвет неба, потому что он поглощает свет за пределами видимого спектра. Здесь, на Земле, влияние светопоглощающих веществ часто игнорируется. Но в случае других планет от него отказаться нельзя. Например, обычная окраска Нептуна и Урана вызвана присутствием большого количества метана в их атмосфере. Метан поглощает красный свет, что даёт синий оттенок. В оставшейся части туториала мы будем игнорировать коэффициент поглощения, однако добавим способ «подкрашивания» атмосферы.

Почему Солнце стало красным во время урагана Офелия 2017 года?

Если вы живёте в Великобритании, то могли заметить, что во время урагана Офелия солнце становилось красным. Так происходило потому, что Офелия принесла песок из Сахары. Эти крошечные частицы, висевшие в воздухе, усиливали эффект рассеяния. Как мы увидим в следующей части, синий свет рассеивается сильнее, чем красный.

Если посмотреть на цвета видимого спектра (ниже), то легко увидеть, что если рассеивается достаточное количество синего света, то небо и в самом деле может стать жёлтым или красным.

Есть искушение сказать, что цвет окраски неба связан с оттенком жёлтого сахарского песка. Однако такой же эффект можно увидеть во время больших пожаров из-за частиц дыма, которые обычно близки к чёрному цвету.

Часть 3. Математика рэлеевского рассеяния.

В этой части мы познакомимся с математикой рэлеевского рассеяния — оптического явления, из-за которого небо выглядит голубым. Выведенные в этой части уравнения мы перенесём в код шейдера следующей части.

Введение

В предыдущей части мы вывели уравнение, представляющее собой хорошую основу для аппроксимации атмосферного рассеяния в шейдере. Однако мы упустили то, что одно уравнение не даст нам убедительных результатов. Если нам нужен красиво выглядящий атмосферный шейдер, то нужно немного углубиться в математику.

Взаимодействие между светом и материей невероятно сложно, и нам не удастся полностью описать его лёгким способом. На самом деле, моделирование атмосферного рассеяния очень трудоёмко. Часть проблемы вызвана тем, что атмосфера не является однородной средой. Её плотность и состав значительно меняются как функция от высоты, что делает практически невозможным создание «идеальной» модели.

Именно поэтому в научной литературе приводится несколько моделей рассеяния, каждая из которых предназначена для описания подмножества оптических явлений, возникающих при определённых условиях. Большинство оптических эффектов, демонстрируемых планетами, можно воссоздать, учитывая всего две разные модели: рэлеевского рассеяния и рассеяния света сферической частицей. Эти два математических инструмента позволяют прогнозировать рассеяния света на объектах различного размера. Первая моделирует отражение света молекулами кислорода и азота, составляющими бОльшую часть состава воздуха. Последняя моделирует отражение света в более крупных структурах, присутствующих в нижних слоях атмосферы, таких как пыльца, пыль и загрязнители.

Рэлеевское рассеяние является причиной голубого неба и красных закатов. Рассеяние света сферической частицей придаёт облакам их белый цвет. Если вы хотите знать, как это происходит, то нам придётся глубже погрузиться в математику рассеяния.

Рэлеевское рассеяние

Какова судьба фотона, ударяющегося о частицу? Чтобы ответить на этот вопрос, нам нужно перефразировать его более формально. Представим, что луч света проходит сквозь пустое пространство и внезапно сталкивается с частицей. Результат такого столкновения сильно зависит от размера частицы и цвета светового луча. Если частица достаточно мала (размером с атомы или молекулы), то поведение света лучше прогнозируется с помощью рэлеевского рассеяния.

Что же происходит? Часть света продолжает свой путь, «не ощутив» никакого влияния. Однако небольшой процент этого исходного света взаимодействует с частицей и рассеивается во всех направлениях. Однако не все направления получают одинаковое количество света. Фотоны с большей вероятностью проходят прямо через частицу или отражаются назад. То есть вариант отражения фотона на 90 градусов менее велик. Такое поведение можно увидеть на схеме ниже. Голубой линией показаны наиболее вероятные направления рассеянного света.

Это оптическое явление математически описывается уравнением рэлеевского рассеяния $S \left(\lambda, \theta, h \right )$ , которое даёт нам долю исходного света $I_0$ , отражённую в направлении $\theta$ :

$I = I_0 \, S \left(\lambda, \theta, h\right)$

$S \left(\lambda, \theta, h\right ) = \frac{\pi^2 \left(n^2-1 \right )^2}{2} \underset{\text{density}}{\underbrace{\frac{\rho\left(h\right)}{N}}} \overset{\text{wavelength}}{\overbrace{\frac{1}{\lambda^4}}} \underset{\text{geometry}}{\underbrace{\left(1+\cos^2\theta \right )}}$

Где:

$\lambda$ : длина волны (wavelength) приходящего света;
$\theta$ : угол рассеияния (scattering angle);
: высота (altitude) точки;
: коэффициент преломления воздуха;
$N=2.504 \cdot 10^{25}$ : количество молекул на кубический метр стандартной атмосферы;
$\rho\left(h\right)$ : коэффициент плотности.Это число на уровне моря равно , и экспоненциально уменьшается с увеличением . Об этой функции можно многое сказать, и мы рассмотрим её в следующих частях.

Но это не уравнение рэлеевского рассеяния!

Если вы встречались с рэлеевским рассеянием не в области компьютерной графики, то есть вероятность, что вы видели другое уравнение. Например, представленное в статье «Рэлеевское рассеяни» на Википедии, сильное отличается.

Использованное в этом туториале уравнение взято из научной статьи Display of The Earth Taking into Account Atmospheric Scattering, Нишиты et al.

Откуда взялась эта функция?

Одна из задач этого блога — объяснение вывода всех получаемых величин. К сожалению, это не относится к рэлеевскому рассеянию.

Если вам всё-таки интересно разобраться, почему частицы света так странно отражаются от молекул воздуха, то интуитивное понимание происходящего может дать следующее объяснение.

Причиной рэлеевского рассеяния на самом деле является не «отталкивание» частиц. Свет — это электромагнитная волна, и она может взаимодействовать с неравновесием зарядов, присутствующим в определённых молекулах. Эти заряды насыщаются поглощением получаемого электромагнитного излучения, которое позже испускается снова. Показанная в угловой функции двудольная форма показывает, как молекулы воздуха становятся электрическими диполями, излучающими подобно микроскопическим антеннам.

Первое, что можно заметить в рэлеевском рассеянии — это то, что в некоторых направлениях распространяется больше света, чем в других. Второй важный аспект заключается в том, что количество рассеянного света сильно зависит от длины волны $\lambda$ приходящего света. Показанная ниже круговая диаграмма визуализирует $S \left(\lambda, \theta, 0\right )$ для трёх разных длин волн. Вычисление $S$ при $h=0$ часто называется рассеянием на уровне моря.

На рисунке ниже показана визуализация коэффициентов рассеяния для непрерывного диапазона длин волн/цветов видимого спектра (код доступен в ShaderToy).

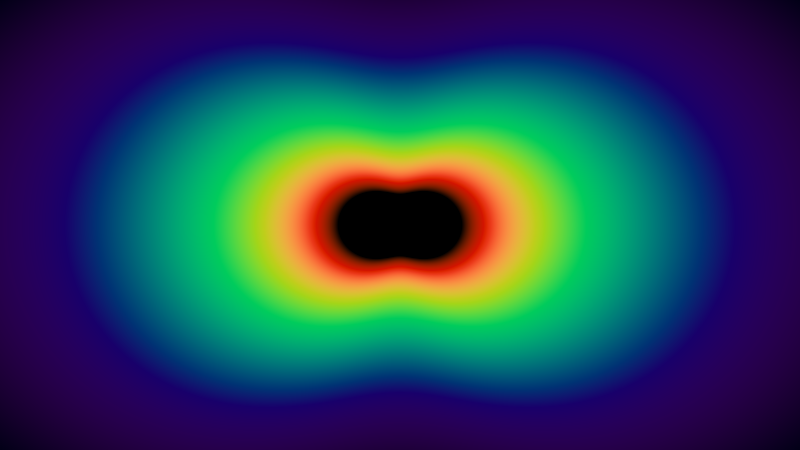
Центр изображения выглядит чёрным, потому что длины волн в этом диапазоне находятся за пределами видимого спектра.

Коэффициент рэлеевского рассеяния

Уравнение рэлеевского рассеяния показывает, какое количество света рассеивается в определённом направлении. Однако оно не говорит нам, сколько энергии всего рассеялось. Для вычисления этого нам нужно учесть рассеивание энергии во всех направлениях. Вывод уравнения нелёгок; если вы не освоили сложный матанализ, то вот результат:

$\beta \left(\lambda, h \right )=\frac{8\pi^3 \left(n^2-1 \right )^2}{3} \frac{\rho\left(h\right)}{N} \frac{1}{\lambda^4}$

Где $\beta \left(\lambda, h \right )$ показывает долю энергии, которая теряется из-за рассеяния после столкновения с одной частицей. Часто эту величину называют коэффициентом рэлеевского рассеяния.

Если вы читали предыдущую часть туториала, то можете догадаться, что $\beta$ на самом деле является коэффициентом затухания, который использовался в определении пропускания $T\left(\overline{AB}\right)$ на отрезке $\overline{AB}$ .

К сожалению, вычисление $\beta$ очень затратно. В шейдере, который мы собираемся написать, я постараюсь экономить как можно больше вычислений. По этой причине полезно будет «извлечь» из коэффициента рассеяния все множители, которые являются константами. Что даёт нам $\beta \left(\lambda\right )$ , который называется коэффициентом рэлеевского рассеяния на уровне моря ( $h=0$ ):

$\beta \left(\lambda \right )=\frac{8\pi^3 \left(n^2-1 \right )^2}{3} \frac{1}{N} \frac{1}{\lambda^4}$

Покажите мне вычисления!

Уравнение рэлеевского рассеяния показывает нам долю энергии, рассеиваемой в определённом направлении. Чтобы вычислить полные потери, нам нужно учитывать все возможные направления. Для суммирования на непрерывном интервале требуется интегрирование.

Можно попробовать проинтегрировать $S \left(\lambda, \theta, h\right )$ по $\theta$ на интервале $\left[0,2\pi\right]$ , но это будет ошибкой.

Несмотря на то, что мы визуализировали рэлеевское рассеяние в двух измерениях, на самом деле это трёхмерное явление. Угол рассеяния $\theta$ может принимать любое направление в 3D-пространстве. Вычисления с учётом полного распределения функции, которое зависит от $\theta$ в трёхмерном пространстве (как $S$ ) называется интегрированием по телесному углу:

$\beta \left(\lambda, h \right ) = \int_{0}^{2\pi} \int_{0}^{\pi} S \left(\lambda, \theta, h \right ) \sin\theta \, d\theta d\phi$

Внутренний интеграл перемещает $\theta$ в плоскости XY, а внешний — поворачивает результат вокруг оси X, чтобы учесть третье