[Перевод] Объясняем p-значения для начинающих Data Scientist’ов
Я помню, когда я проходил свою первую зарубежную стажировку в CERN в качестве практиканта, большинство людей все еще говорили об открытии бозона Хиггса после подтверждения того, что он соответствует порогу «пять сигм» (что означает наличие p-значения 0,0000003).
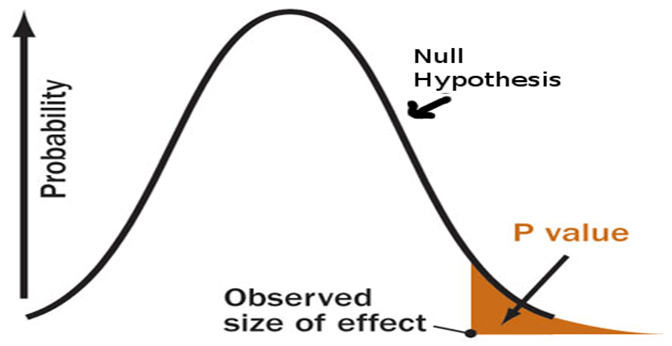
Тогда я ничего не знал о p-значении, проверке гипотез или даже статистической значимости.
Я пошел, чтобы гуглить слово — p-значение, и то, что я нашел в Википедии, заставило меня еще больше запутаться…
При проверке статистических гипотез p-значение или значение вероятности для данной статистической модели-это вероятность того, что при истинности нулевой гипотезы статистическая сводка (например, абсолютное значение выборочной средней разницы между двумя сравниваемыми группами) будет больше или равна фактическим наблюдаемым результатам.
— Wikipedia
Хорошая работа Википедия.
Ладно. Я не понял, что на самом деле означает р-значение.
Углубившись в область науки о данных, я наконец начал понимать смысл p-значения и то, где его можно использовать как часть инструментов принятия решений в определенных экспериментах.
Поэтому я решил объяснить р-значение в этой статье, а также то, как его можно использовать при проверке гипотез, чтобы дать вам лучшее и интуитивное понимание р-значений.
Также мы не можем пропустить фундаментальное понимание других концепций и определение p-значения, я обещаю, что сделаю это объяснение интуитивно понятным, не подвергая вас всеми техническими терминами, с которыми я столкнулся.
Всего в этой статье четыре раздела, чтобы дать вам полную картину от построения проверки гипотезы до понимания р-значения и использования его в процессе принятия решений. Я настоятельно рекомендую вам пройтись по всем из них, чтобы получить подробное понимание р-значений:
- Проверка гипотезы
- Нормальное распределение
- Что такое P-значение?
- Статистическая значимость
Это будет весело.
Давайте начнем!
1. Проверка гипотез
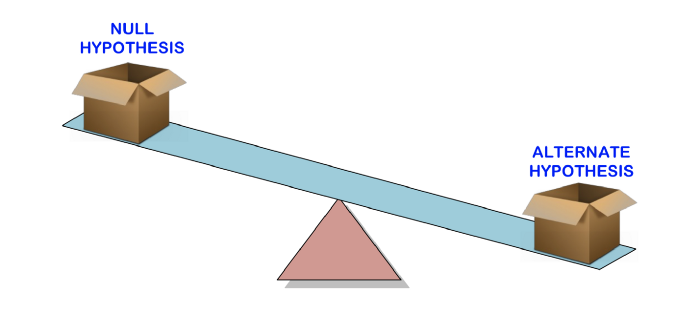
Прежде чем мы поговорим о том, что означает р-значение, давайте начнем с разбора проверки гипотез, где р-значение используется для определения статистической значимости наших результатов.
Наша конечная цель — определить статистическую значимость наших результатов.
И статистическая значимость построена на этих 3 простых идеях:
- Проверка гипотезы
- Нормальное распределение
- P-значение
Проверка гипотез используется для проверки обоснованности утверждения (нулевой гипотезы), сделанного в отношении совокупности с использованием выборочных данных. Альтернативная гипотеза — это та, в которую вы бы поверили, если бы нулевая гипотеза оказалась неверной.
Другими словами, мы создадим утверждение (нулевая гипотеза) и используем пример данных, чтобы проверить, является ли утверждение действительным. Если утверждение не соответствует действительности, мы выберем альтернативную гипотезу. Все очень просто.
Чтобы узнать, является ли утверждение обоснованным или нет, мы будем использовать p-значение для взвешивания силы доказательств, чтобы увидеть, является ли оно статистически значимым. Если доказательства подтверждают альтернативную гипотезу, то мы отвергнем нулевую гипотезу и примем альтернативную гипотезу. Это будет объяснено в следующем разделе.
Давайте воспользуемся примером, чтобы сделать эту концепцию более ясной, и этот пример будет использоваться на протяжении всей этой статьи для других концепций.
Пример. Предположим, что в пиццерии заявлено, что время их доставки составляет в среднем 30 минут или меньше, но вы думаете, что оно больше чем заявленное. Таким образом, вы проводите проверку гипотезы и случайным образом выбираете время доставки для проверки утверждения:
- Нулевая гипотеза — среднее время доставки составляет 30 минут или меньше
- Альтернативная гипотеза — среднее время доставки превышает 30 минут
- Цель здесь состоит в том, чтобы определить, какое утверждение — нулевое или альтернативное — лучше подтверждается данными, полученными из наших выборочных данных.
Мы будем использовать односторонний тест в нашем случае, так как нам важно только, чтобы среднее время доставки превышало 30 минут. Мы не будем учитывать эту возможность в другом направлении, поскольку последствия того, что среднее время доставки будет меньше или равно 30 минутам, еще более предпочтительны. Здесь мы хотим проверить, есть ли вероятность того, что среднее время доставки превышает 30 минут. Другими словами, мы хотим посмотреть, не обманул ли нас пиццерия.
Одним из распространенных способов проверки гипотез является использование Z-критерия. Здесь мы не будем вдаваться в подробности, так как хотим лучше понять, что происходит на поверхности, прежде чем погрузиться глубже.
2. Нормальное распределение
Нормальное распределение — это функция плотности вероятности, используемая для просмотра распределения данных.
Нормальное распределение имеет два параметра — среднее (μ) и стандартное отклонение, также называемое сигма (σ).
Среднее — это центральная тенденция распределения. Оно определяет местоположение пика для нормальных распределений. Стандартное отклонение — это мера изменчивости. Оно определяет, насколько далеко от среднего значения склонны падать значения.
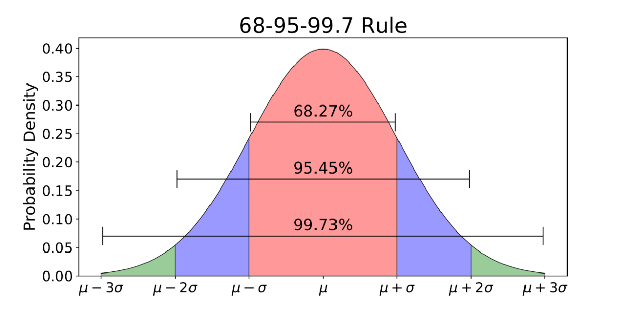
Нормальное распределение обычно связано с правилом 68–95–99.7 (изображение выше).
- 68% данных находятся в пределах 1 стандартного отклонения (σ) от среднего значения (μ)
- 95% данных находятся в пределах 2 стандартных отклонений (σ) от среднего значения (μ)
- 99,7% данных находятся в пределах 3 стандартных отклонений (σ) от среднего значения (μ)
Помните порог «пять сигм» для открытия бозона Хиггса, о котором я говорил в начале? 5 сигм — это около 99,99999426696856% данных, которые должны быть попасть до того, как ученые подтвердили открытие бозона Хиггса. Это был строгий порог, установленный, чтобы избежать любых возможных ложных сигналов.
Классно. Теперь вы можете задаться вопросом: «Как нормальное распределение относится к нашей предыдущей проверке гипотез?»
Поскольку мы использовали Z-тест для проверки нашей гипотезы, нам нужно вычислить Z-баллы (которые будут использоваться в нашей тестовой статистике), которые представляют собой число стандартных отклонений от среднего значения точки данных. В нашем случае каждая точка данных — это время доставки пиццы, которое мы получили.

Обратите внимание, что когда мы рассчитали все Z-баллы для каждого времени доставки пиццы и построили стандартную кривую нормального распределения, как показано ниже, единица измерения на оси X изменится с минут на единицу стандартного отклонения, так как мы стандартизировали переменную, вычитая среднее и деля его на стандартное отклонение (см. формулу выше).
Изучение стандартной кривой нормального распределения полезно, потому что мы можем сравнить результаты теста с «нормальной» популяцией со стандартизированной единицей в стандартном отклонении, особенно когда у нас есть переменная, которая поставляется с различными единицами.
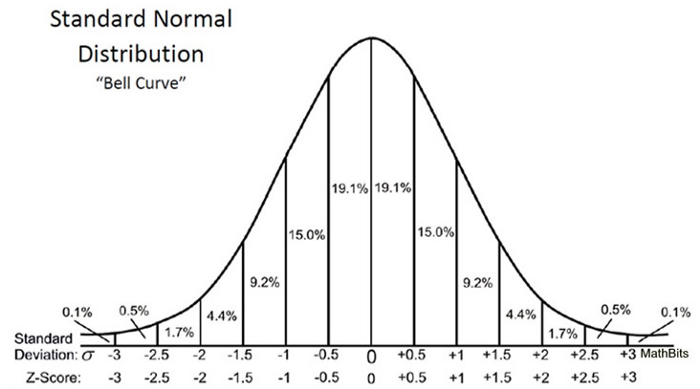
Z-оценка может сказать нам, где лежат общие данные по сравнению со средней популяцией.
Мне нравится, как Уилл Кёрсен выразился: чем выше или ниже Z-показатель, тем менее вероятным будет случайный результат и тем более вероятным будет значимый результат.
Но насколько высокий (или низкий) показатель считается достаточно убедительным, чтобы количественно оценить, насколько значимы наши результаты?
Кульминация
Здесь нам нужен последний элемент для решения головоломки — p-значение, и проверить, являются ли наши результаты статистически значимыми на основе уровня значимости (также известного как альфа), который мы установили перед началом нашего эксперимента.
3. Что такое P-значение?
Наконец… Здесь мы говорим о р-значение!
Все предыдущие объяснения предназначены для того, чтобы подготовить почву и привести нас к этому P-значению. Нам нужен предыдущий контекст и шаги, чтобы понять это таинственное (на самом деле не столь таинственное) р-значение и то, как оно может привести к нашим решениям для проверки гипотезы.
Если вы зашли так далеко, продолжайте читать. Потому что этот раздел — самая захватывающая часть из всех!
Вместо того чтобы объяснять p-значения, используя определение, данное Википедией (извини Википедия), давайте объясним это в нашем контексте — время доставки пиццы!
Напомним, что мы произвольно отобрали некоторые сроки доставки пиццы, и цель состоит в том, чтобы проверить, превышает ли время доставки 30 минут. Если окончательные доказательства подтверждают утверждение пиццерии (среднее время доставки составляет 30 минут или меньше), то мы не будем отвергать нулевую гипотезу. В противном случае мы опровергаем нулевую гипотезу.
Поэтому задача p-значения — ответить на этот вопрос:
Если я живу в мире, где время доставки пиццы составляет 30 минут или меньше (нулевая гипотеза верна), насколько неожиданными являются мои доказательства в реальной жизни?
Р-значение отвечает на этот вопрос числом — вероятностью.
Чем ниже значение p, тем более неожиданными являются доказательства, тем более нелепой выглядит наша нулевая гипотеза.
И что мы делаем, когда чувствуем себя нелепо с нашей нулевой гипотезой? Мы отвергаем ее и выбираем нашу альтернативную гипотезу.
Если р-значение ниже заданного уровня значимости (люди называют его альфа, я называю это порогом нелепости — не спрашивайте, почему, мне просто легче понять), тогда мы отвергаем нулевую гипотеза.
Теперь мы понимаем, что означает p-значение. Давайте применим это в нашем случае.
P-значение в расчете времени доставки пиццы
Теперь, когда мы собрали несколько выборочных данных о времени доставки, мы выполнили расчет и обнаружили, что среднее время доставки больше на 10 минут с p-значением 0,03.
Это означает, что в мире, где время доставки пиццы составляет 30 минут или меньше (нулевая гипотеза верна), есть 3% шанс, что мы увидим, что среднее время доставки, по крайней мере, на 10 минут больше, из-за случайного шума.
Чем меньше p-значение, тем более значимым будет результат, потому что он с меньшей вероятностью будет вызван шумом.
В нашем случае большинство людей неправильно понимают р-значение:
Р-значение 0,03 означает, что есть 3% (вероятность в процентах), что результат обусловлен случайностью — что не соответствует действительности.
Люди часто хотят получить определенный ответ (в том числе и я), и именно поэтому я долго путался с интерпретацией p-значений.
Р-значение ничего не *доказывает*. Это просто способ использовать неожиданность в качестве основы для принятия разумного решения.
— Кэсси Козырков
Вот как мы можем использовать p-значение 0,03, чтобы помочь нам принять разумное решение (ВАЖНО):
- Представьте, что мы живем в мире, где среднее время доставки всегда составляет 30 минут или меньше — потому что мы верим в пиццерию (наше первоначальное убеждение)!
- После анализа времени доставки собранных образцов р-значение на 0,03 ниже, чем уровень значимости 0,05 (предположим, что мы установили это значение перед нашим экспериментом), и мы можем сказать, что результат является статистически значимым.
- Поскольку мы всегда верили пиццерии, что она может выполнить свое обещание доставить пиццу за 30 минут или меньше, нам теперь нужно подумать, имеет ли это убеждение смысл, поскольку результат говорит нам о том, что пиццерия не выполняет свое обещание и результат является статистически значимым.
- Так что же нам делать? Сначала мы пытаемся придумать любой возможный способ сделать наше первоначальное убеждение (нулевая гипотеза) верным. Но поскольку пиццерия постепенно получает плохие отзывы от других людей и часто приводит плохие оправдания, которые привели к задержке доставки, даже мы сами чувствуем себя нелепо, чтобы оправдать пиццерию, и, следовательно, мы решаем отвергнуть нулевую гипотезу.
- Наконец, следующее разумное решение — не покупать больше пиццы в этом месте.
К настоящему времени вы, возможно, уже что-то поняли… В зависимости от нашего контекста, p-значения не используются, чтобы что-либо доказать или оправдать.
По моему мнению, p-значения используются в качестве инструмента для оспаривания нашего первоначального убеждения (нулевая гипотеза), когда результат является статистически значимым. В тот момент, когда мы чувствуем себя нелепо с нашим собственным убеждением (при условии, что р-значение показывает, что результат статистически значим), мы отбрасываем наше первоначальное убеждение (отвергаем нулевую гипотезу) и принимаем разумное решение.
4. Статистическая значимость
Наконец, это последний этап, когда мы собираем все вместе и проверяем, является ли результат статистически значимым.
Недостаточно иметь только р-значение, нам нужно установить порог (уровень значимости — альфа). Альфа всегда должна быть установлена перед экспериментом, чтобы избежать смещения. Если наблюдаемое р-значение ниже, чем альфа, то мы заключаем, что результат является статистически значимым.
Основное правило — установить альфа равным 0,05 или 0,01 (опять же, значение зависит от вашей задачи).
Как упоминалось ранее, предположим, что мы установили альфа равным 0,05, прежде чем мы начали эксперимент, полученный результат является статистически значимым, поскольку р-значение 0,03 ниже, чем альфа.
Для справки ниже приведены основные этапы всего эксперимента:
- Сформулируйте нулевую гипотезу
- Сформулируйте альтернативную гипотезу
- Определите значение альфа для использования
- Найдите Z-показатель, связанный с вашим альфа-уровнем
- Найдите тестовую статистику, используя эту формулу
- Если значение тестовой статистики меньше Z-показателя альфа-уровня (или p-значение меньше альфа-значения), отклоните нулевую гипотезу. В противном случае не отвергайте нулевую гипотезу.
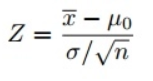
Если вы хотите узнать больше о статистической значимости, не стесняйтесь посмотреть эту статью — Объяснение статистической значимости, написанная Уиллом Керсеном.
Последующие размышления
Здесь много чего нужно переваривать, не так ли?
Я не могу отрицать, что p-значения по своей сути сбивают с толку многих людей, и мне потребовалось довольно много времени, чтобы по-настоящему понять и оценить значение p-значений и то, как они могут быть применены в рамках нашего процесса принятия решений в качестве специалистов по данным.
Но не слишком полагайтесь на p-значения, поскольку они помогают только в небольшой части всего процесса принятия решений.
Я надеюсь, что мое объяснение p-значений стало интуитивно понятным и полезным в вашем понимании того, что в действительности означают p-значения и как их можно использовать при проверке ваших гипотез.
Сам по себе расчет р-значений прост. Трудная часть возникает, когда мы хотим интерпретировать p-значения в проверке гипотез. Надеюсь, что теперь трудная часть станет для вас немного легче.
Если вы хотите узнать больше о статистике, я настоятельно рекомендую вам прочитать эту книгу (которую я сейчас читаю!) — Практическая статистика для специалистов по данным, специально написанная для data scientists, чтобы разобраться с фундаментальными концепциями статистики.

Узнайте подробности, как получить востребованную профессию с нуля или Level Up по навыкам и зарплате, пройдя платные онлайн-курсы SkillFactory:
