[Перевод] Новое доказательство приближает математиков к подтверждению любимой гипотезы Эрдёша
Два математика доказали первый этап любимой гипотезы Эрдёша о закономерностях в последовательностях чисел

Пара математиков доказала первую часть одной из наиболее знаменитых гипотез, касающихся аддитивных свойств целых чисел. Её более 60 лет назад предложил легендарный венгерский математик Пал Эрдёш. Звучит она так: в какой момент в бесконечном списке целых чисел гарантированно появятся закономерности из не менее трёх идущих на одном расстоянии друг от друга чисел — к примеру, 26, 29 и 32.
Эрдёш за свою карьеру сформулировал тысячи задач, однако вопрос того, в каком списке чисел содержатся числа, находящиеся на равных расстояниях друг от друга (то, что математики называют арифметическими прогрессиями), был одним из его любимых. «Думаю, многие люди считали это главной задачей Эрдёша», — сказал Тимоти Гауэрс из Кембриджского университета. Гауэрс, получивший филдсовскую премию в 1998 году, много часов потратил на попытки решить эту задачу. «Практически все достаточно амбициозные специалисты по аддитивной комбинаторике пытались её решить», — сказал он, имея в виду отрасль математики, к которой принадлежит эта гипотеза.
У более плотных списков чисел, как правило, больше шансов содержать арифметическую прогрессию, чем у более разреженных. Поэтому Эрдёш предложил простую проверку на плотность списка: сложить величины, обратные тем, что есть в списке. Если чисел будет достаточно много, чтобы сделать эту сумму бесконечной, то, по предположению Эрдёша, в списке должно будет присутствовать бесконечное количество арифметических прогрессий любой конечной длины — по три, четыре и т.д. чисел подряд.
В работе, опубликованной в онлайне 7 июля Томас Блум из Кембриджа и Олаф Сисаск из Стокгольмского университета доказали эту гипотезу в случае равномерно расставленных троек чисел — таких, как 5, 7 и 9. Эта пара показала, что когда сумма обратных чисел к числам списка бесконечна, в нём должно найтись бесконечно много троек равноотстоящих друг от друга чисел.

Томас Блум из Кембриджа
«Этот результат стал самым примечательным за много лет», сказал Нетс Кац из Калифорнийского технологического университета. «Это значимое событие».
Одно из множеств, сумма обратных чисел к которым устремляется в бесконечность, это простые числа — те, что делятся только на 1 и себя. В 1930-х Йоханнес ван дер Корпут использовал особую структуру простых чисел, чтобы показать, что в них действительно можно найти бесконечное множество равноотстоящих друг от друга троек (к примеру, 17, 23 и 29).
Однако новое открытие Блума и Сисаска означает, что не нужно глубоко разбираться в уникальной структуре простых чисел для того, чтобы доказать, что в них найдётся бесконечное множество троек. Достаточно знать только, что простых чисел достаточно много для того, чтобы сумма обратных к ним значений была бесконечной –, а это математикам известно уже много столетий. «Результат Томаса и Олафа говорит нам о том, что даже если бы их структура совершенно отличалась от той, что у них есть реально, простой факт наличия их большого количества гарантировал бы бесконечность арифметических прогрессий», — написал нам Том Сандерс из Оксфордского университета.
Длина новой работы — 77 страниц, и на тщательную её проверку у математиков уйдёт какое-то время. Однако многие оптимистично считают её верной. «Она реально выглядит так, как должно выглядеть доказательство этого утверждения», — сказал Кац, чьи ранние работы легли в основу данной.
Теорема Блума и Сисаска говорит о том, что если список чисел достаточно плотный, в нём должны проявиться определённые закономерности. Это открытие соответствует фундаментальному девизу математики, как называет его Сара Пилюс из Оксфорда, первые сформулированному Теодором Моцкином: «Абсолютного беспорядка не бывает».
Замаскированная плотность
Довольно легко создать бесконечный список без арифметических прогрессий, если сделать его достаточно разреженным. К примеру, рассмотрим последовательность 1, 10, 100, 1,000, 10 000, … Обратные величины дают в сумме 1,111(1). Расстояние между этими числами так быстро растёт, что ни одной тройки чисел, расположенных на равном расстоянии друг от друга, найти не удастся.
Однако вы можете задаться вопросом: существует ли более плотный список чисел, в котором всё равно нет арифметических прогрессий. Можно, к примеру, идти по числовой прямой и оставлять каждое число, не входящее в арифметические прогрессии. Получим последовательность 1, 2, 4, 5, 10, 11, 13, 14, … которая на первый взгляд выглядит довольно плотной. Однако со временем она становится всё более разреженной — к примеру, когда мы доберёмся до 20-значных чисел, мы будем брать с числовой прямой лишь 0,000009% из всех целых чисел. В 1946 году Феликс Беренд придумал и более плотные примеры, но и они очень быстро становятся ра зреженными — множество Беренда, дойдя до 20-значных чисел, содержит только 0,001% из всех целых.
С другой стороны, если в вашем множестве будут почти все целые числа, то в нём определённо найдутся арифметические последовательности. Но между двумя этими крайностями лежит огромная, почти неразмеченная срединная территория. Насколько разреженным может быть множество, размышляли математики, чтобы там всё равно ещё гарантированно могли найтись арифметические прогрессии?

Олаф Сисаск из Стокгольмского университета
Эрдёш (как говорят, возможно, совместно с венгерским математиком Палом Тураном) дал один возможный ответ. Его условие по поводу суммы обратных величин — это замаскированная плотность. Оказывается, это то же самое, что сказать, что плотность списка вплоть до числа N не меньше, чем единица, делённое на количество цифр в N. Иначе говоря, ваш лист может становиться всё более разреженным по мере продвижения по числовой прямой, но только если это происходит очень медленно. На 5-значных числах плотность вашего списка должна быть не менее 1/5; на 20-значных — не менее 1/20, и так далее. И если это условие выполняется, то, как предположил Эрдёш, в вашем списке должно найтись бесконечное количество арифметических прогрессий любой длины.
В 1953 году Клаус Рот направил математиков на путь, ведущий к доказательству гипотезы Эрдёша. В работе, благодаря которой в том году он получил филдсовскую премию, он определил функцию плотности, гарантирующую наличие равноотстоящих троек чисел. Плотность была не такой низкой, как у Эрдёша, но всё же приближавшейся к нулю при продвижении по числовой прямой. Теорема Рота означала, что в списке чисел, чья плотность в итоге падает ниже 1%, а потом ниже 0,1%, а потом ниже 0,01%, и так далее, обязательно должны найтись арифметические прогрессии, если только его плотность падает достаточно медленно.

Пал Эрдёш читает лекцию »60 лет в математике» в Кембриджском университете в июне 1991 года.
В первую очередь подход Рота основывался на том, что большинству списков с выбранной им плотностью «хочется» иметь арифметические прогрессии — у них есть достаточно разных пар чисел для того, чтобы почти наверняка некоторые из средних точек между этими парами тоже оказались в этом списке, что привело бы к появлению равноотстоящих троек. Хитрость в том, как перейти от списка из «почти всех» чисел к списке «всех» чисел, при том, что вся структура могла быть специально сконструированной таким образом, чтобы избежать арифметических прогрессий.
Получив такой список, Рот придумал, как сделать «дистилляцию» его структуры через разметку его «частотного спектра» при помощи преобразования Фурье. Оно показывает, какие из возникающих закономерностей проявляются особенно сильно — та же математика лежит в основе таких технологий, как рентгеновская кристаллография и радиоспектроскопия.
Некоторые частоты проявляются сильнее других, а эти вариации подчёркивают имеющиеся закономерности — к примеру, частота может говорить о том, что в списке содержится больше нечётных чисел, чем чётных. Если так, то можно сконцентрироваться только на нечётных числах, и получить более плотный список по сравнению со списком, состоящим только из нечётных чисел. Рот смог показать, что после нескольких таких дистилляций получится настолько плотный список, что в нём обязательно должны будут присутствовать арифметические прогрессии.
Подход Рота вдохновил множество работ в аналитической теории чисел за последние пятьдесят лет, говорит Джейкоб Фокс из Стенфордского университета. «Его идеи были очень влиятельными».
Гейм, сет, матч
Однако метод Рота работал только для тех множеств чисел, которые уже изначально были довольно плотными — в противном случае постоянные дистилляции просто испаряли все числа. Другие математики постоянно находили способы использовать этот метод всё более и более эффективно, однако никак не могли приблизиться к плотности, описанной в гипотезе Эрдёша. «Это препятствие выглядело очень сложным», — сказал Фокс.
Затем в 2011 году Кац и Майкл Бейтмэн придумали, как преодолеть это препятствие в более простых условиях: в карточной игре Сет, где игроки ищут наборы из трёх карт, размеченных разными символами. Тройку из игры Сет можно определить как арифметическую прогрессию, и, как и в случае со списком целых чисел, можно задать вопрос, какую долю всех карт нужно выложить на стол, чтобы наверняка нашлась хотя бы одна тройка.
Игра «Сет»
Цель игры — найти особые тройки карт, или «сеты», в колоде из 81 карты. У каждой карты есть свой рисунок с четырьмя свойствами — цвет (красный, фиолетовый, зелёный), форма (овал, ромб, волна), закраска (контур, полоски, полностью закрашенный) и число фигур (одна, две или три). В обычной игре на стол выкладываются 12 карт лицом вверх, и игроки ищут наборы из трёх карт, в которых каждый из четырёх атрибутов либо совпадает у всех карт, либо отличается у всех карт. Если среди 12 карт не находится таких сетов, добавляются ещё карты.
Вся колода
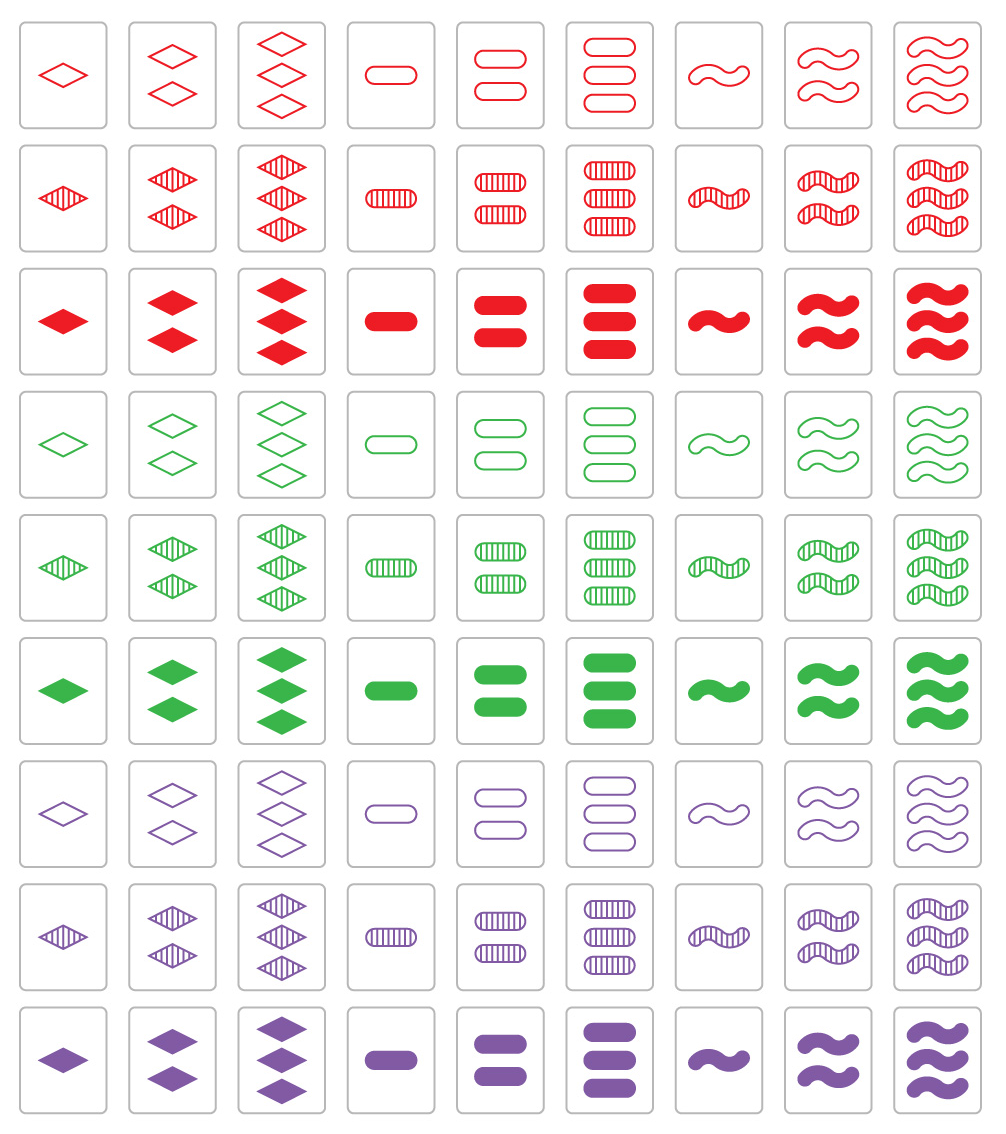
Есть сет, нет сета — примеры
Карты без троек
Простой способ собрать достаточно большой набор карт без троек — брать только карты, в которых есть только два или три варианта выбора для каждого атрибута. Размер этой коллекции составит (2/3)n от всей колоды, где n — количество атрибутов.

Этот вопрос (связанный не только со стандартной игрой Сет, но и с её более крупными вариантами) — естественная модель для изучения соответствующего вопроса, касающегося целых чисел. Поэтому математики понадеялись, что прорыв Бейтмэна и Каца сможет открыть дорогу к доказательству гипотезы Эрдёша, особенно в комбинации с другими недавними прорывами. Вскоре после выхода работы Бейтмэна и Каца Гауэрс запустил «проект эрудит» — массивную совместную коллаборацию, призванную сделать такую попытку.
Однако проект быстро застопорился. «В нём собралось огромное количество технических аргументов, — сказал Гауэрс. — Этот проект больше подходил для одного-двух человек, долго и не спеша работающих над ним».
К счастью, пара математиков как раз готовилась к этому. Блум и Сисаск, сначала по отдельности, уже начали задумываться над гипотезой Эрдёша, пленённые красотой используемых в ней техник. «Это была одна из первых исследовательских задач, с которыми я столкнулся», — сказал Сисаск, которому, как и Блуму, сейчас около 35 лет.
Блум и Сисаск объединили усилия в 2014 году, а к 2016 решили, что близки к решению. Блум даже объявил об этом на своей лекции, и только после этого обнаружил, что некоторые из найденных ими обходных путей оказались неверными. Парочка продолжала работу, погружаясь в метод Бейтмэна и Каца, и в итоге поняла, какие новые идеи позволили бы им перенести этот метод из мира игры Сет в мир целых чисел.
Новая работа, судя по всему, корректна со все сторон, сказал Кац. «Предыдущим их заявлениям я не верил, а этому верю».
Работа Блума и Сисаска — это «огромное достижение», сказал Фокс. Им и другим математикам уже не терпится выяснить, применимы ли техники из новой работы к решению других задач. «Думаю, что эти методы очень сильно повлияют на математику», — сказал Фокс.
Что до гипотезы Эрдёша целиком, работа над ней ещё далека от завершения. Блум и Сисаск доказали эту гипотезу только для равноотстоящих друг от друга троек чисел, но не для более длинных арифметических прогрессий — эта задача пока остаётся вне досягаемости.
И даже вопрос с тройками, который Блум и Сисаск уже закрыли, по мнению многих математиков, не особенно помогает. Как бы ни было трудно доказать, что плотность Эрдёша гарантирует наличие равноотстоящих троек чисел, математики подозревают, что реальная плотность, при которой эта гарантия перестаёт работать, гораздо ниже — возможно, чуть выше, чем плотность множеств, которые конструировал Беренд.
«Нельзя сказать, что мы полностью решили эту задачу, — сказал Блум. — Мы пролили на неё чуть больше света».
Блум и Сисаск, вероятно, выжали из текущих методов всё возможное, сказал Фокс. «Должны появиться какие-то совершенно новые инструменты, которые позволят продвинуться значительно дальше и получить кардинально лучший результат», — сказал он. Однако «это ещё, вероятно, не конец истории».
