[Перевод] Норберт Винер: рассеянный отец кибернетики
Когда мы встретились, я шел в студенческий клуб или из него? Спрашиваю, потому что во втором случае я уже пообедал.
Американский математик Норберт Винер был во всех отношениях своеобразным человеком. Закончив среднюю школу в 11 лет, он поступил в Колледж Тафтса и всего через три года стал бакалавром математики. Еще до наступления совершеннолетия Гарвард удостоил Винера докторской степени за его диссертацию по математической логике. Вот какую характеристику ему дает Сильвия Назар:
Американский Джон фон Нейман, выдающийся эрудит, который сделал потрясающий вклад в чистую математику, а затем начал вторую и столь же поразительную карьеру в прикладной математике.
Винер был тем самым человеком, который ввел современное значение слова «feedback» («обратная связь»), изобретая кибернетику, а кибернетика, в свою очередь, дала жизнь таким революционным понятиям как искусственный интеллект, компьютерное зрение, робототехника, нейрология (в ключе нейросетей) и многим другим.

Но, несмотря на колоссальные достижения на научном поприще, Винер гораздо сильнее запомнился современникам своими необычными личностными качествами. Согласно его биографии, этот великий человек провел 30 лет «блуждая по коридорам MIT утиной походкой». Без сомнения, он был одним из самых рассеянных ученых-математиков в мире.
Его кабинет находился в нескольких шагах по коридору от моего и он часто заходил ко мне, чтобы поговорить. Когда мой кабинет несколько лет спустя перенесли в другое место, он зашел, чтобы представиться. Он не понимал, что я был тем самым человеком, которого он так часто навещал; Я был в новом кабинете, поэтому он думал, что я был кем-то другим.
— Филлис Л. Блок
Однажды он отправился на конференцию, а свою машину оставил на большой стоянке. Когда конференция закончилась, он вышел на улицу, но забыл, где припарковался. Он даже забыл, как выглядела его машина. Поэтому он решил подождать, пока все не разъедутся, после чего забрал оставшийся автомобиль.
— Говард Ив
Примечание. Перевод статьи содержит малозначительные сокращения, которые были произведены с целью сделать материал более интересным и удобным для восприятия. В частности, убраны повторы некоторых фактов и сугубо научные фрагменты. С полным статьи текстом на английском языке вы можете ознакомиться по ссылке на оригинал.
Ранние годы (1894–1909)

Норберт Винер в возрасте семи лет, 1901 год
Норберт Винер родился в 1894 году в штате Миссури, в еврейской семье. Его отец, Лео Винер, к моменту рождения сына уже был достаточно известным ученым историком-языковедом. В 1880 году он закончил университет в Варшаве, а затем берлинский Университет Фридриха Вильгельма. Будучи полиглотом, отец Норберта свободно владел несколькими языками. Как пишет в своей автобиографии «Ex Prodigy» сам Норберт, мультилингвизм во времена детства его отца был едва ли не традицией:
Немецкий был языком семьи, а русский — языком государства. […] Он выучил французский язык как язык культурного общества;, а в Восточной Европе, особенно в Польше, все еще оставались те, кто в лучших традициях ренессанса предпочитал для культурного общения итальянский.
Однако его отец возвел эту традицию в абсолют. К десяти годам Лео уже без проблем мог изъясняться на дюжине языков. В течение своей жизни он освоил порядка 34 языков, включая гэльский, различные индейские диалекты и даже язык африканской группы народов Банту.

Лео и Берта Винеры
Со своей женой и матерью Норберта Лео познакомился, работая учителем в Канзас Сити. В 1883 он сделал ей предложение. Как вспоминают жители городка, в котором поселилась пара, Берта была «невысокой, миловидной женщиной, […] практичной, общительной и хозяйственной». Они поженились в 1893 году, всего за год до рождения Норберта. Имя сыну было дано в честь главного героя драматической поэмы Роберта Браунинга «На балконе».
Одаренный мальчик
Когда ему было всего 18 месяцев, девочка, подрабатывающая у нас няней, развлекалась тем, что рисовала буквы на прибрежном песке. Она обратила внимание, что Норберт внимательно наблюдает за ее действиями и в шутку решила научить его алфавиту. Пару дней спустя она с величайшим удивлением сообщила мне, что Норберт освоил алфавит в совершенстве.

Девятилетний Норберт Винер
Мать Норберта с самого раннего возраста читала ему книги. А к трем годам Норберт уже сам мог читать для нее вслух. Лео, к тому моменту ставший профессором в Гарварде, начал понемногу обучать его предметам из своей области. Юный Норберт очень любил научные книги и в качестве подарка на третий день рождения получил копию «Естественной истории» Вуда, которую буквально проглотил всего за несколько дней.
Обучение под руководством отца началось еще в дошкольном возрасте. Как вспоминал потом Норберт, его уроки состояли преимущественно из неформальных лекций по профилю отца (то есть языки и литература), включая греческих и римских классиков, любимых немецких поэтов Лео и трудов философов, таких как Дарвин и Хаксли. На минуточку, Норберту еще не было даже шести лет от роду!
Несмотря на то, что его сын был чрезвычайно одарен, Лео был требовательным учителем и сразу же задал высокую планку. Когда Норберт ошибался, отец тут же становился «невероятно критичен и суров». Вот что он пишет в своей автобиографии:
Алгебра всегда давалась мне легко, хотя методы, избранные отцом для преподавания, едва ли способствовали моему душевному покою. Каждую ошибку следовало исправлять незамедлительно. Разговор с ним мог начаться в спокойном и доброжелательном тоне —, но ровно до того момента, как я впервые ошибался. Тут же из нежного и любящего отца он превращался в кровного врага.
Несмотря на совсем юный возраст и физическую незрелость, к семи годам отец отдал Норберта на обучение в прогрессивную школу Пибоди (Кембридж, Массачусетс). Без оглядки на возраст он поступил сразу в третий класс, а вскоре был переведен в четвертый, но возникли кое-какие проблемы. Его навыки чтения были безупречны, но, как ни парадоксально, интерес к математике стал угасать. Понимая, что это — следствие того, что Норберту скучно зубрить упражнения, Лео незамедлительно забрал его из школы и в течение еще трех лет продолжал свой «радикальный эксперимент по домашнему обучению».
Самый выдающийся мальчик в мире (1906)

Обложка New York World
Впервые мир узнал о Норберте Винере 7 октября 1906 года, когда портрет мальчика-гения оказался на первой полосе New York World под заголовком «Самый выдающийся мальчик в мире». В статью вошли интервью с Норбертом и его отцом, поданные в тоне явного одобрения нетрадиционного подхода Лео к раннему детскому развитию:
Мальчик Норберт выучил все буквы в восемнадцать месяцев. Под началом своего отца он начал читать [по-английски] в три, по-гречески и на латыни — в пять, а вскоре еще и по-немецки. В семь лет он изучал химию, в девять — алгебру, геометрию, тригонометрию, физику, ботанику и зоологию, а этой осенью, в одиннадцать лет, он поступил в Колледж Тафтса в соседнем городе Медфорд после всего лишь трех с половиной лет формального обучения.
— отрывок из статьи «Самый выдающийся мальчик в мире» в New York World, 7 октября 1906 г.
Отношения между Норбертом и Лео
Мой самый близкий ментор и дражайший противник.
Вот что пишет физик Фриман Дайсон в эссе «Трагическая история гения» в The New York Review of Books, 2005:
Пока он рос, стараясь избежать клейма одаренного малыша из Тафтса и Гарварда, Лео только всё усугублял, крича об успехах Норберта во всех газетах и журналах.

Именно так все и было: отец Лео трубил во все концы о своих идеях в области образования: помимо статьи в New York World, он писал в Boston Evening Record, Американский журнал по педиатрии и American Magazine. Лео Винер даже «не скрывал, что намеренно выращивает из Норберта и его сестер гениев.
Профессор Лео Винер из Гарвардского университета […] считает, что секрет раннего умственного развития заключается в раннем обучении. […] Он отец четверых детей в возрасте от четырех до шестнадцати лет; и у него достаточно смелости, чтобы заявлять, что он хочет сделать их предметами образовательного эксперимента. Результаты […] поразительны, особенно в случае с его старшим сыном, Норбертом.
— выдержка из American Magazine, июль 1911.
Норберт ленив и учится меньше, чем средний мальчишка его возраста.
— Лео Винер, 1906.
Согласно методологии Лео, его публичные заявления существенно разнились с тем, что он говорил собственному сыну. К примеру, если прочитать собственные заметки отца Норберта о том, как его дети стали такими талантливыми, складывается ощущение, что похвала и признание способностей детей в его картине мира играли совсем ничтожную роль.
Глупо заявлять, как это делают многие, что Норберт, Констанс и Берта — необычайно одаренные дети. Ничего подобного. Если они и знают больше, чем другие дети их возраста, то только потому что их учили иначе.

Слева — Лео Винер, справа — посвящение Норберта своему отцу бестселлера «Человеческое использование человеческих существ»
Более того, собственные сочинения Норберта дают понять, что на него негативно повлияли заявления отца:
Я чувствовал, что отец не избежал соблазна давать интервью обо мне и моем обучении […]. В этих интервью он подчеркнул, что я был по сути обычным мальчиком, которого превосходно натаскали.
Ощущение того, что отец буквально «создал» его, в сочетании с отсутствием признания его талантов, усилий и жертв, оставило неизгладимый след на Винере.
Однако из интервью с Лео в статье в New York World становится понятно, что его отец на самом деле понимал, насколько его сын одарен, но ему не хотелось признавать это при Норберте:
Я не люблю говорить о сыне, но вовсе не из-за того, что не горжусь им, а потому, что это может дойти до его ушей и испортить его. У него острый аналитический ум и фантастическая память. Он учится не просто за счет зубрежки, как попугай, а рассуждает.
Образование (1903–1913)
После домашнего обучения у отца в возрасте 9 лет Норберт поступил в среднюю школу Айера, а потом пошел еще дальше:
Вскоре стало ясно, что большая часть моей учебы относится к третьему году старшей школы, поэтому, когда год закончился, я был переведен в старшие классы.
После выпуска в 1906 году отец «решил […] отправить его в Колледж Тафтса, чтобы не подвергать его рискованной нагрузке вступительных экзаменов в Гарвард». Норберт, которому на тот момент было 12, прилежно слушался отца.
Университет Тафтса (1906–1909)
Совсем еще юный Винер поступил в Колледж Тафтса в штате Массачусетс осенью 1906 года. Он изучал там греческий и немецкий языки, физику, математику, а также биологию:
Несмотря на свой интерес к биологии, я получил математическое высшее образование. Я изучал математику каждый год в колледже […], находя исчисления и дифференциальные уравнения довольно легкими. Я имел обыкновение обсуждать их с моим отцом, который отлично разбирался в обычной математической программе колледжа.
Он закончил Тафтс с отличием и получил степень бакалавра в 1909 году, когда ему было 14 лет.

Выпускные фотографии из Колледжа Тафтса в 1909 году и Гарвардского университета в 1913 году
Гарвардский университет (1909–1913)
Мне было почти пятнадцать лет, и я решил попробовать себя в докторантуре по биологии.
После окончания колледжа Винер поступил в аспирантуру Гарвардского университета (где работал его отец) для изучения зоологии. И это несмотря на возражения Лео, который «не давал своего согласия. Он думал, что я мог бы пойти в медицинскую школу». Однако работа в лаборатории в сочетании с плохим зрением Винера сделали зоологию крайне трудным для него делом. «Бунт» Норберта продлился недолго, и через некоторое время он решил последовать совету своего отца и заняться философией.
Как обычно, это решение было принято моим отцом. Он решил, что успех, которого я добился в качестве студента в Университете Тафтса в области философии, ясно говорит о моем истинном поприще. Я должен был стать философом.
Винеру предложили стипендию в Sage School of Philosophy в Корнеллском университете и перевели туда в 1910 году. Однако после этого «черного года», в течение которого он чувствовал себя неуверенно и неуместно, он вернулся в Гарвардский университет. Изначально он собирался работать с философом Джосайей Ройсом (1855–1916) для получения степени доктора философии в математической логике, но из-за болезни последнего Винеру пришлось обратиться к своему бывшему профессору из Колледжа Тафтса, Карлу Шмидту. Шмидт, как позже писал Винер, был тогда «молодым человеком, жадно интересовавшимся математической логикой». Именно он вдохновил Винера провести сравнение реляционной алгебры Эрнста Шредера (1841–1902) и Principia Mathematica Рассела и Уайтхеда.
Его диссертация по философии, в высшей степени математическая, была посвящена формальной логике. Ключевые результаты были опубликованы в следующем 1914 году в статье «Упрощение в логике отношений» в трудах Кембриджского философского общества. На следующую осень Винер отправился в Европу для постдокторской работы в надежде, что в конечном итоге он сможет занять постоянную должность на факультете одного из самых известных университетов Америки.
Постдокторская работа (1913–1915)
Вслед за защитой докторской диссертации и выпуском из Гарварда восемнадцатилетний Винер был удостоен престижной возможности в течение года учиться за рубежом. Он выбрал британский Кембридж.
Кембриджский университет (1913–1914)
Лео Винер за ручку привел сына к Бертрану Расселу
Норберт Винер прибыл в Тринити-Колледж, Кембридж, в сентябре 1913 года. Вместе с ним приехала вся его семья под предводительством отца, Лео, который расценивал шанс присоединиться к сыну в Европе как внеочередной шаббат. Как пишут Конвей и Зигельман, «юный Винер шагнул в ворота Тринити-Колледжа, мекки современной философии и новой математической логики, а следом за ним шел его отец».
Винер отправился в Кембридж, чтобы продолжить изучение философии с одним из авторов Principia Mathematica, которая была объектом его гарвардской диссертации. Лорд Бертран Рассел (1872–1970), на тот момент сорокалетний мужчина, к 1913 году считался самым прогрессивным философом англоамериканского мира, чей монументальный трехтомный труд, написанный совместно с Альфредом Нортом Уайтхедом и опубликованный в 1910, 1912 и 1913 годах, был тепло принят научным сообществом. Principia (или PM, как ее часто сокращенно называют) на тот момент была наиболее полным и последовательным трудом по математической философии.
Несмотря на то, что Норберта воспитывал полиглот Лео, его первое впечатление о Расселе с его свирепым нравом оставляло желать лучшего. Позже он писал своему отцу:
Отношение Рассела [ко мне] кажется мне смесью безразличия и презрения. Думаю, я буду вполне доволен тем, что увижу на его лекциях.
В свою очередь, впечатление Рассела о Винере, ну или по крайней мере то, что он демонстрировал, кажется весьма симметричным. «Очевидно, что молодой Винер не воспринимает информацию не занимается философией так, как это предписывает титан Тринити.»
Выдержка из письма Норберта Винера Лео Винеру (1913):
С моей курсовой работой под руководством мистера Рассела все в порядке, но я совершенно разочарован тем, что я делаю под его руководством в частном порядке. Думаю, что как философ я неудачник […]. Рассел, кажется, очень недоволен […] моими философскими способностями и лично мной. Он говорил о моих взглядах как об «ужасном тумане», […], что изложение моих взглядов даже хуже, чем сами взгляды и […] обвинил меня в чрезмерной, петушиной самоуверенности […] Несмотря на то, что он извинился, это самые жестокие слова.
На самом деле, мнение Рассела о Норберте не было настолько суровым, насколько тому казалось (чего нельзя было, к сожалению, сказать о Лео). В своих личных документах Рассел одобрительно отмечал юношу, а после прочтения диссертации Норберта сказал, что это «очень хорошая техническая работа» и подарил ему копию третьего тома «PM».
Однако самое важное, что вынес Винер из совместной работы с Расселом, не имело отношения ни к физике, ни к философии. По воле божьей Винеру попались на глаза четыре статьи 1905 года физика Альберта Эйнштейна, идеи которых он позже использовал в своей работе. Сам же Винер в свое время выделил Г.Х. Харди (1877–1947) как ученого, оказавшего на него самое глубокое влияние:
Курс Харди […] был откровением для меня […] [в его] внимании к строгости […] За все годы прослушивания лекций по математике я никогда не встречал кого-то равного Харди ни в ясности изложения, ни в увлекательности, ни в интеллектуальной силе. Если уж говорить о ком-то как о моем мастере в области математического мышления, это должен быть Г.Х. Харди.
В частности, Винер выражал Харди благодарность за то, что тот познакомил его с интегралом Лебега, который «привел меня прямиком к главному достижению моей только начинающейся карьеры».
Геттингенский университет (1914)
Приобретя еще одну порцию опыта, в 1914 Винер продолжил учиться уже в Геттингенском университете. Он прибыл туда весной, сделав лишь краткую остановку в Мюнхене, чтобы встретиться с семьей. Отучится там он только один семестр, но этот период будет иметь решающее значение для всего его дальнейшего развития в качестве математика. Винер принимается за изучение дифференциальных уравнений под руководством Дэвида Гильберта (1862–1943), возможно, самого выдающегося математика своей эпохи, которого Винер позже назовет «по-настоящему вселенским гением математики».
Винер оставался в Геттингене до начала Первой мировой войны, до июня 1914 года, а затем решил вернуться в Кембридж и продолжить изучение философии с Расселом.
Карьера (с 1915 года)
До того, как Винера приняли в MIT, где он и оставался до конца своей жизни, ему довелось потрудиться на нескольких случайных работах в разных отраслях промышленности и городах. Официально он вернулся в Соединенные Штаты в 1915 году, некоторое время прожил Нью-Йорке, продолжая изучать философию в Колумбийском университете у философа Джона Дьюи (1859–1952). После этого преподавал курс философии в Гарварде и поступил на работу в качестве младшего инженера в General Electric. После того, как его отец получил там место штатного писателя, «убедившись в том, что с его неуклюжестью он никогда не добьется успеха в инженерном деле», Норберт присоединился к Encyclopedia Americana в Олбани, штат Нью-Йорк. Также в течение какого-то времени Винер работал в Boston Herald.
Когда Америка вступила в Первую мировую войну, Винер захотел внести свою лепту и в 1916 году посетил учебный лагерь для офицеров, но в конечном итоге провалил комиссию. В 1917 году он снова попытался вступить в армию, но снова безуспешно, на сей раз из-за плохого зрения. Через год математик Освальд Веблен (1880–1960) пригласил Винера помочь фронту и поработать над баллистикой в Мэриленде:
Я получил срочную телеграмму от профессора Освальда Веблена с нового испытательного полигона в Абердине, штат Мэриленд. Это был мой шанс заняться настоящей военной работой. Ближайшим поездом я отправился в Нью-Йорк, где пересел на экспресс до Абердина.

Математики на Абердинском полигоне, 1918 год
Опыт на испытательном полигоне, как пишет Дайсон, преобразил Винера. До приезда он был 24-летним математическим вундеркиндом, которого отговаривали от математики из-за неудачного опыта его преподавательской работы в Гарварде. Назад он вернулся воодушевленный тем, как всё, чему он научился, можно применить в решении настоящих мировых проблем:
Мы жили в странной атмосфере, где должность, армейское звание и ученая степень имели [равное] значение, и лейтенант мог обращаться к рядовому, называя его «доктор», или выполнял приказы сержанта. Когда мы не были заняты работой на шумных машинах для ручных вычислений, которые у нас назывались «крашерами», мы часами играли в бридж и на тех же самых машинах записывали результаты. Что бы мы ни делали, мы всегда говорили о математике.
Математика (с 1914 года)
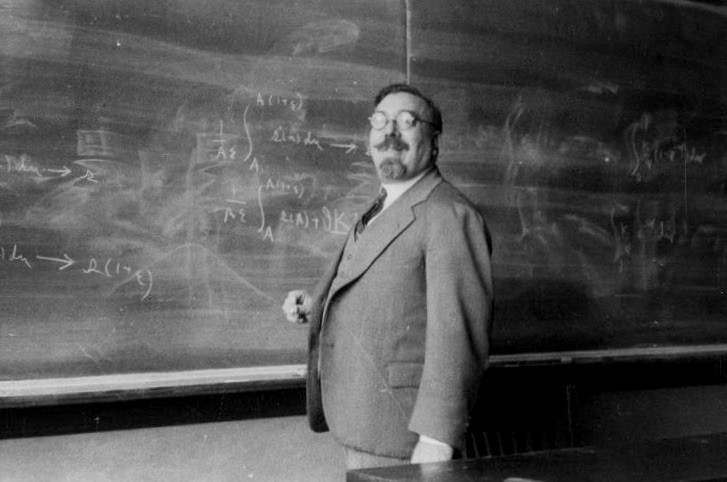
В обширном списке опубликованных работ первые две статьи Винера о математике (на текущий момент вторая утрачена) появились в семнадцатом выпуске Трудов Кембриджского философского общества от 1914 года:
- Wiener, N. (1914). «A Simplification of the Logic of Relations». Proceedings of the Cambridge Philosophical Society 17, pp. 387–390.
- Wiener, N. (1914). «A Contribution to the Theory of Relative Position». Proceedings of the Cambridge Philosophical Society 17, pp. 441–449.
Однако наиболее известные математические работы Винера были написаны им преимущественно в возрасте от 25 до 50 лет, то есть в 1921–1946 гг.
После окончания Первой мировой войны Винер попытался получить положение в Гарварде, но был отвергнут, вероятно, из-за антисемитских настроений, превалирующих в университете в то время, что часто связывают с влиянием Г.Д. Биркгофа (1884–1944). Вместо этого в 1919 году Винер занял должность лектора в MIT. С этого момента результативность его исследований значительно возросла.
За первые пять лет своей карьеры в Массачусетском технологическом институте он опубликовал 29 (!) журнальных статей, заметок и сообщений в различных областях математики, подписанных одним автором. В их числе:
- Wiener, N. (1920). «A Set of Postulates for Fields». Transactions of the American Mathematical Society 21, pp. 237–246.
- Wiener, N. (1921). «A New Theory of Measurement: A Study in the Logic of Mathematics». Proceedings of the London Mathematical Society, pp. 181–205.
- Wiener, N. (1922). «The Group of the Linear Continuum». Proceedings of the London Mathematical Society, pp. 181–205.
- Wiener, N. (1921). «The Isomorphisms of Complex Algebra». Bulletin of the American Mathematical Society 27, pp. 443–445.
- Wiener, N. (1923). «Discontinuous Boundary Conditions and the Dirichlet Problem». Transactions of the American Mathematical Society, pp. 307–314.
Винеровский процесс (1920–23)
Винер впервые заинтересовался броуновским движением, когда учился в Кембридже у Рассела. Он и познакомил Винера с работами Альберта Эйнштейна. В своем труде 1905 года «Uber die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in Ruhended Flüssigkeiten suspendierten Teilchen» Эйнштейн смоделировал необычное движение частицы пыльцы под воздействием отдельных молекул воды. Это «необычное движение» впервые наблюдалось ботаником Робертом Броуном в 1827 году, но еще не было формально исследовано в математике.
Винер подошел к этому феномену с точки зрения того, что «было бы математически интересно разработать меру вероятности для наборов траекторий»:
Прототипом проблемы, рассмотренной Винером, является поступь пьяницы: выпивший мужчина сначала опирается на фонарный столб; затем он делает шаг в каком-то направлении — это может быть короткий или длинный шаг; затем он либо стоит, сохраняя равновесие, либо делает еще один шаг в каком-то направлении; и так далее. Путь, который он выберет, будет сложным, с множество изменений направления. […] Предполагая, что человек не имеет априорных предпочтений к какому-либо определенному направлению или определенному размеру шага и может двигаться быстро или медленно в соответствии со своей прихотью, есть ли способ назначить меру вероятности для любого конкретного набора траекторий?
— выдержка, Джон фон Нейман и Норберт Винер в книге Стива Хеймса, 1980
Винер расширил формулировку броуновского движения Эйнштейна, чтобы описать эти траектории, и таким образом установил связь между мерой Лебега (систематический способ присвоения чисел подмножествам) и статистической механикой. То есть Винер предоставил математическую формулировку для описания одномерных кривых, оставленных броуновскими процессами. Его работа, которую теперь в его честь часто называют винеровским процессом, была опубликована в серии статей, разработанных в период между 1920 и 1923 годом:
- Wiener, N. (1920). «The Mean of a Functional of Arbitrary Elements». Annals of Mathematics 22 (2), pp. 66–72.
- Wiener, N. (1921). «The Average of an Analytic Functional». Proceedings of the National Academy of Sciences 7 (9), pp. 253–260.
- Wiener, N. (1921). «The Average of an Analytic Functional and the Brownian Movement». Proceedings of the National Academy of Sciences 7 (10), pp. 294–298.
- Wiener, N. (1923). «Differential Space». Journal of Mathematics and Physics 2, pp. 131–174.
- Wiener, N. (1924). «The Average Value of a Functional». Proceedings of the London Mathematical Society 22, pp. 454–467.

Норберт Винер и Макс Борн, 1925 год
Возвращение в Геттинген (1924–1926)
В силу особенностей своей работы в начале 1920-х каждым летом с 1924 по 1926 Винер возвращается в Геттинген, причем в последний год — в качестве лауреата стипендии Гуггенхайма. В разгар так называемого золотого века квантовой физики его пребывание в Геттингене совпадало с приездами фон Неймана (которого Винер знал лично и состоял с ним в переписке) и Дж. Роберта Оппенгеймера.
Летом 1925 года Винер читал в Геттингене группе математиков, как студентов, так и вольнослушателей, лекции о своей деятельности, а позже написал домой, что Гильберт сказал о его работе sehr schön («очень хорошая»). К концу пребывания Винера в университете глава математического факультета Ричард Курант (1888–1972) сказал ему, что если он вернется в следующем году, то получит должность приглашенного профессора.
Теорема Винера — Хинчина (1930)
Сразу после Геттингена Винер начал работать в сфере прикладной математики, а в 1930 году — над так называемыми автокорреляционными функциями, которые обеспечивают корреляцию между сигналом и задержанной копией этого сигнала в зависимости от задержки. Теорема Винера — Хинчина показывает, как автокорреляционная функция Rₓₓ (τ) связана со спектральной плотностью мощности Sₓₓ (f) через преобразование Фурье:
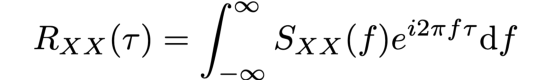
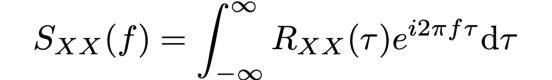
Результат был опубликован в том же году, и Винера повысили до доцента MIT:
- Wiener, N. (1930). «Generalized Harmonic Analysis». Acta Mathematica. 55, pp. 117–258.

Слева — Норберт Винер, справа — оглавление работы «Обобщенный гармонический анализ»
Тауберова теорема Винера (1932)
Несмотря на то, что к началу 30-х годов он уже всерьез занимался обработкой сигналов и первыми разработками в области электротехники, Винер продолжал публиковать статьи по чистой математике, включая работу по анализу пространств Лебега. Тауберова теорема Винера, опубликованная в 1932 году, обеспечивает необходимое и достаточное условие, при котором любая функция в L₁ или L₂ может быть аппроксимирована линейными комбинациями сдвигов данной функции.

Норберт Винер в своем кабинете в MIT
Теоремы Пэли — Винера (1934)
Винер руководил несколькими кандидатами наук. Один из них, Норман Левинсон (1912–1975), рассказывает о своем опыте сотрудничества с великим человеком:
Он был самым вдохновляющим учителем. Работая с доской, он на самом деле продолжал свои собственные исследования. Как только я начал разбираться в его работе, он передал мне рукопись Пэли — Винера на доработку. Я нашел упущение в доказательстве и доказал лемму, чтобы исправить это. Затем Винер сел за пишущую машинку, напечатал мою лемму, поставил мое имя и отправил всё в журнал.
— отрывок, Джон фон Нейман и Норберт Винер, Хеймс, 1980
Кибернетика (с 1947 года)

Информация — это информация, а не материя или энергия.
Область науки, которая теперь неотделима от имени Винера, во многом стала результатом интереса Норберта к стохастическим и математическим шумовым процессам, которые рассматриваются как в электротехнике, так и в теории связи. В лекции, озаглавленной «Люди, машины и мир вокруг них», Винер рассказывает, что его новаторская работа появилась в результате попытки внести свой вклад в военные действия 1940-х годов:
Было два сходящихся потока идей, которые привели меня в кибернетику. Один из них — тот факт, что в ходе последней войны, когда она уже явно шла, но, во всяком случае, до Перл-Харбора, когда мы еще не были вовлечены в конфликт, я пытался выяснить, могу ли я найти свое место в военных действиях того времени.
Как сам Винер заявляет в своей лекции, его первые опыты в зарождающейся тогда теории цифровых вычислений не давали результатов настолько, чтобы быть полезными в ведении этой войны, поэтому Винер начал искать что-то новое. Его вторая инициатива была связана с вооружением, в частности с противовоздушной обороной:
Я оглянулся по сторонам и заметил, что важной в то время темой была противовоздушная оборона. Это было […] время, когда выживание хоть кого-нибудь, кто мог бороться с Германией, казалось, зависело от противовоздушной обороны.
Да, зенитная пушка — очень интересный инструмент. Во время Первой мировой войны зенитное орудие было разработано для стрельбы, однако под рукой все еще нужно было держать таблицы дальности, чтобы выстрелить. Это означало, что требовалось всё рассчитать, пока самолет пролетает прямо над головой. И к тому времени, когда вы оказывались в состоянии что-то сделать, самолет уже пропадал из вида.

Итак, продолжает Винер, «это приводит к очень интересным математическим теориям. У меня нашлись некоторые идеи, доказавшие затем свою пользу». Он работал над этой проблемой с Джулианом Бигелоу (1913–2003).
В начале 1941 года два человека заняли пустую аудиторию на втором этаже математического факультета, корпус 2, комната 244, и принялись за работу на доске. Винер излагал своему новому коллеге проблему управления огнем.
— Конвей и Зигельман, 2005.
Винер и Бигелоу рассматривали наводчика, орудие, самолет и пилота как интегрированную вероятностную систему. Теория вероятности была на стороне пилота: в 1940 году только один из примерно 2500 зенитных снарядов попадал в цель. В предварительном отчете они объяснили, что намереваются «поставить анализ проблемы прогнозирования на чисто статистическую основу, определив, в какой степени движение цели предсказуемо на основе известных фактов и истории наблюдений, а также в какой степени движение цели непредсказуемо.
— отрывок, Turing’s Cathedral by George Dyson, 2012
Аудиозапись лекции Винера «Люди, машины и мир вокруг них» 1950 года, Винер начинает говорить в 13:30.
Фильтр Винера (1942)
Работа Винера над проблемой управления зенитным огнем привела к изобретению фильтра, используемого для вычисления статистической оценки неизвестного сигнала путем получения его на входе и фильтрации на выходе. Фильтр основан на нескольких результатах прошлых работ Винера на тему интегралов и преобразований Фурье. Хотя фильтр был разработан в Радиационной лаборатории MIT, результат был опубликован только в секретном документе. Первый открытый документ, описывающий фильтр, появился в книге Винера 1949 года «Экстраполяция, интерполяция и сглаживание стационарных временных рядов».
Война закончилась, и в 1947 году Винера пригласили на конгресс по гармоническому анализу, который состоялся в Нанси, Франция. Конгресс был организован тайным французским математическим обществом «Бурбаки» в сотрудничестве с математиком Шолемом Мандельбройтом (1899–1983), дядей Бенуа Мандельброта (1925–2010), позднее открывшего множество Мандельброта. Винеру предложили написать работу об «объединяющем характере той части математики, который обнаруживается при изучении броуновского движения и телекоммуникационной инженерии». В следующем году Винер придумал неологизм «кибернетика», чтобы обозначить изучение таких «телеологических механизмов». Его рукопись послужит основой научно-популярной работы «Кибернетика, или Управление и связь в животном и в машине», опубликованной издательством MIT Press / Wiley and Sons в 1948 году. Книга получила следующие рецензии:
Прекрасно написанная книга, ясная, прямая и, несмотря на всю ее сложность, так же понятная дилетанту, как и ученому, если тот готов отказаться от попыток постичь математические формулы.
— The Saturday Review, 1949
Ее масштаб и вовлеченность захватывают дух и заставляют рецензента поверить, что это важный вклад в современное мышление.
— Philosophy of Science 22, 1955
Будучи одной из самых влиятельных книг двадцатого века, «Кибернетика» провозглашается оригинальным произведением, важность которого сравнима трудами Галилея, Мальтуса, Руссо или Милла.
— The New York Times, 1964
Личность
Он едва понимал, где находится.

Винер дает интервью Чарльзу Ромину для образовательного телешоу CBS
Несмотр
