[Перевод] Найдено доказательство того, что все изменения являются смесью порядка и случайностей
Все описания изменений представляют собой уникальную смесь случайностей и детерминизма, если верить радикальному доказательству «слабой гипотезы Пинскера»
Представьте себе сад, где растут все цветы мира — деликатные орхидеи, возвышающиеся подсолнухи, восковые цветы кактуса карнегия и вонючие соцветия аморфофаллуса титанического. Теперь представьте, что всё это растительное многообразие свелось всего к двум вариантам, и что, скрещивая их, вы можете произвести все остальные.
Такова природа одного из самых радикальных доказательств, полученных за последние годы. Его сделал Тим Остин, математик из Калифорнийского университета в Лос-Анджелесе. Но вместо цветов работа Остина связана с одним из наиболее изученных объектов в математике: математическим описанием изменений.
Эти описания, известные, как динамические системы, применимы ко всему, от движения планет до колебаний рынка акций. Где бы ни возникала динамическая система, математикам хочется понять её основы. И один из базовых фактов состоит в том, что любую сколь угодно сложную динамическую систему можно разбить на случайные и детерминистские элементы.
Этот вопрос является темой «слабой гипотезы Пинскера», которую впервые сформулировали в 1970-х. Доказательство гипотезы, представленное Остином, даёт элегантно интуитивный метод размышления над всяческими непонятными явлениями. Он показал, что по своей сути каждая из этих динамических систем является смесью случайности и детерминизма.
Судьба и случайность
Динамическая система начинается с неких входных данных, например, с положения маятника, применяет некие правила, например, законы движения Ньютона, и выдаёт некий результат, например, положение маятника через одну секунду. Что важно, динамические системы позволяют вам повторять этот процесс: можно взять новое положение маятника, применить те же правила, и получить его положение ещё через секунду.
Также динамические системы бывают и чисто математическими. Можно выбрать начальное число, применить правило «умножить число на два» и получить новое. Эта система также позволяет вам ввести итоговое число обратно в обработчик правил и получить ещё больше чисел.
Определённые типы динамических систем можно выразить в виде комбинации двух более простых динамических систем. Две эти системы работают независимо друг от друга, но их можно объединить, сформировав более сложную. Для примера, представьте динамическую систему, двигающую точку по поверхности цилиндра. Вы вводите положение точки, применяете правила и получаете другую точку.
Эту систему можно разобрать на две простые. Первая — динамическая система, двигающая точку по окружности. Вторая — система, двигающая точку вверх и вниз по вертикали. Скомбинировав две системы — движение по окружности и движение по прямой — мы получим более сложное движение точки по цилиндру.
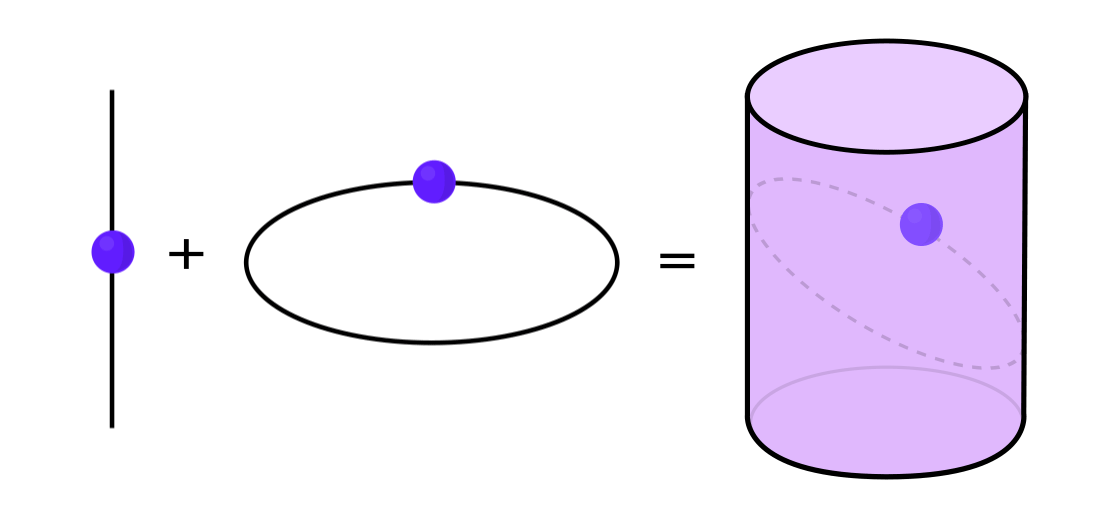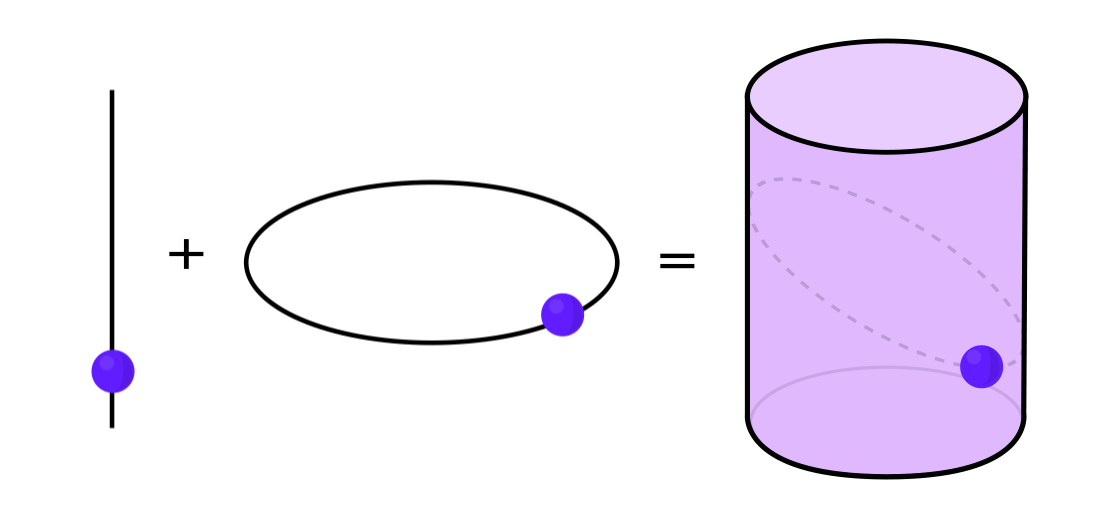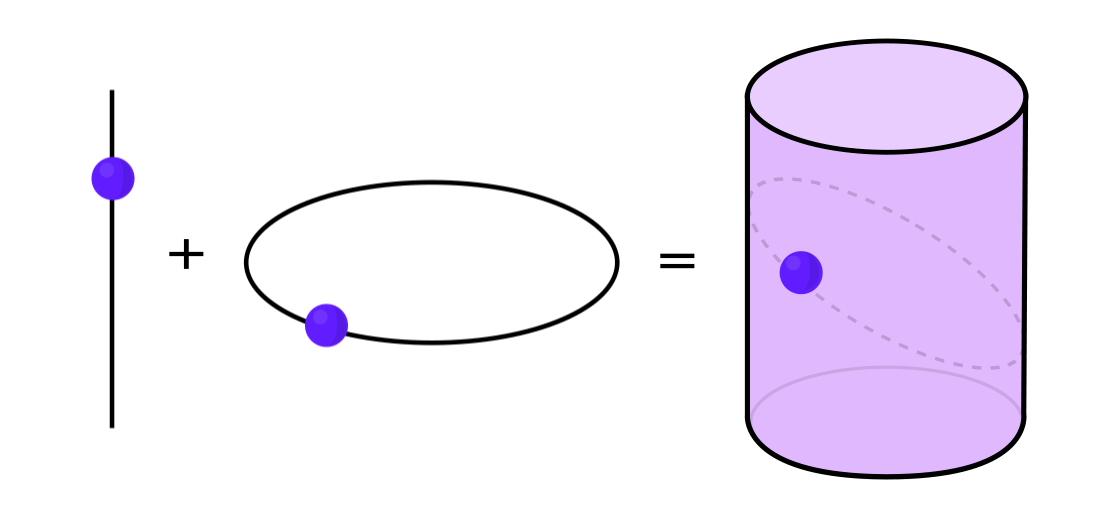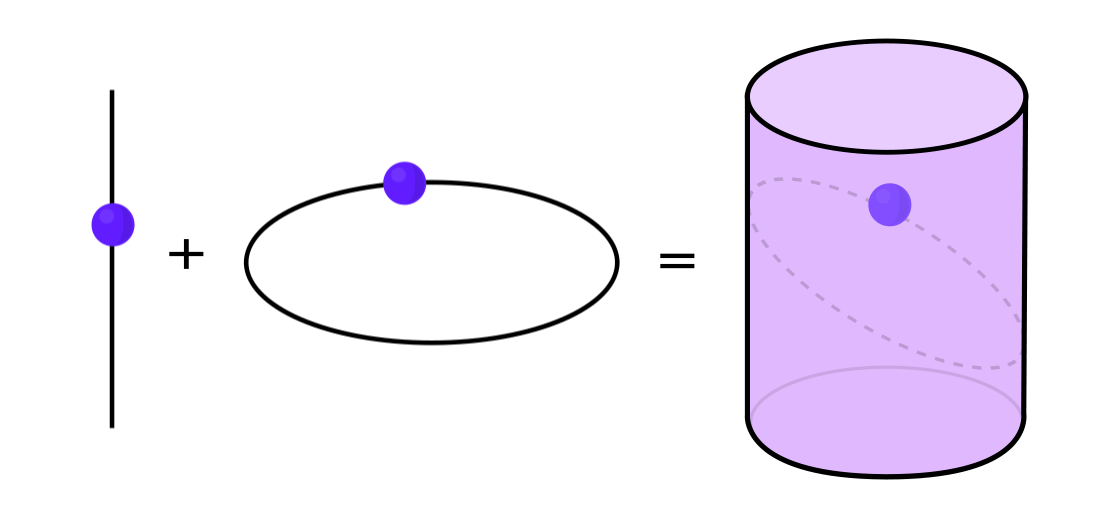
«Вместо того, чтобы изучать всю динамическую систему целиком, вам надо разбить её на части, мелкие части, которые имеет смысл изучать», — сказала Кэтрин Линдси, математик из Бостонского колледжа.
На роль этих строительных блоков есть два естественных кандидата. Первые — полностью детерминированные динамические системы, как наш пример с маятником. Если вы знаете положение маятника в какой-то момент времени, вы можете предсказать его в любой момент будущего.

Жан-Поль Тувено в 1975 году, за два года до формулирования слабой гипотезы Пинскера
Второй тип динамических систем — совершенно случайные. К примеру, представьте динамическую систему с таким правилом: подбросьте монетку. Если будет орёл, сделайте шаг влево; если решка, вправо. Итоговый путь будет совершенно случайным, то есть, даже если вы будете знать всё о предыдущем пути, эта информация никак не поможет вам предсказать следующий шаг.
Некоторые динамические системы совершенно случайные, иные полностью детерминированные, а большинство находится где-то между ними — они являются гибридом обеих. К примеру, представьте немного изменённую версию нашей случайной прогулки. Мы ходим вдоль пути, по краю которого посажены цветы, причём их цвета тоже случайные. Правило остаётся тем же: если выпадает орёл, идём влево; если решка, вправо. Какой будет последовательность цветов цветков?
Сначала вы скажете, что случайной. Ведь цвета-то и сами выбирались случайно, и ваше движение тоже случайно. Однако после того, как вы прошли мимо одного цветка, вероятность того, что вы пройдёте мимо него в будущем, повышается, просто потому, что вы находитесь недалеко от него. Последовательность цветов цветков будет уже не совсем случайной.
«Если вы стоите рядом с красным, это увеличивает шансы, что через два шага вы опять встретитесь с красным, поскольку может случиться так, что вы шагнёте влево, затем вправо, и вернётесь в то же место», — сказал Остин.
Такая «случайная прогулка по случайному пейзажу» выдаёт выходные данные — последовательность цветов — частично случайные, а частично — нет. В 1960 году математик Марк Пинскер предположил, что у определённого большого класса динамических систем есть следующее свойство: они представляют собой смесь случайной динамической системы с детерминированной.
Гипотеза Пинскера применима к классу динамических систем, у которых есть важное общее свойство. Точки в них не отходят далеко друг от друга и не сжимаются в процессе развитии системы. Точнее, если нарисовать петлю вокруг набора точек в вашем пространстве (при этом пространством может быть что-то вроде поверхности цилиндра), запустить развитие динамической системы на большой промежуток времени, а потом нарисовать петлю вокруг получившегося набора точек, то область, которую займут точки в конце, совпадёт с областью, которую они занимали вначале. Такие системы называются «сохраняющими меру»
«Если бы изначальная гипотеза Пинскера оказалась верной, это было бы удивительное описание мира», — сказал Ассаф Наор, математик из Принстонского университета. Но Пинскер ошибался. В 1973 году Дональд Орнстейн опроверг его гипотезу. «Формулировка была слишком амбициозной», — сказала Брина Кра, математик из Северо-западного университета.
В математике часто бывает так, что после того, как общую гипотезу опровергают, математики пытаются сформулировать более скромный её вариант. В 1977 году математик Жан-Поль Тувено предложил слабую гипотезу Пинскера. Он смягчил изначальную формулировку, предположив, что динамические системы, которые имел в виду Пинскер, являются результатом комбинирования чисто случайной системы с системой, почти полностью детерминистской.
Уточнение «почти» отличает гипотезу Тувено от гипотезы Пинскера. Он имел в виду, что у простой детерминистской системы должен быть какой-то след случайности. Этот след может быть исчезающее малым, но должен быть там. И пока он есть, заявил Тувено, идея Пинскера будет работать.
«Это было близко к изначальной гипотезе, и Тувено показал, что если это так, то у гипотезы будет огромное количество прекрасных вариантов применения», — сказал Наор.
В последующие десятилетия математики не достигли больших успехов в деле доказательства слабой гипотезы Пинскера. Отсутствие продвижения заставило Тувено подумать, что даже его ослабленная формулировка окажется неверной. «В один момент я думал, что всё окажется противоположным, что она не будет универсальной», — сказал он.
А потом появился Тим Остин.
Ступенчатое решение
Для доказательства слабой гипотезы Пинскера потребовалось найти точный способ просеивать динамическую систему — такой, который позволил бы отделять её случайные и почти детерминированные части. Предыдущие работы установили, что сложнее всего будет изолировать элементы с небольшой случайностью.
«Небольшие случайные факторы отловить гораздо тяжелее, и это центральная часть доказательства — найти способ обнаружить небольшую случайную структуру», — сказал Тувено.

Тим Остин, математик из Калифорнийского университета в Лос-Анджелесе
Остин сумел разобраться с небольшими случайными элементами динамической системы путём изменения перспективы. Динамические системы работают на непрерывном пространстве, типа точки, двигающейся по поверхности цилиндра, или маятника, качающегося в пространстве. В этих пространствах точки движутся по непрерывным дугам сообразно правилам динамической системы. Также эти системы работают на бесконечном количестве шагов — они могут действовать вечно.
Но в своём доказательстве Остин отказался от непрерывного гладкого пространства и вечной работе динамических систем. Вместо этого он начал анализировать, что произойдёт, если позволить им работать дискретное время, например, миллион шагов. Таким образом он применял метод, придуманный Тувено.
«Главным вкладом Тувено было то, что он понял, что если выполнить правильные математические действия с длинными конечными строками», можно доказать свойства динамической системы, сказал Остин. «Моим главным вкладом было то, что я доказал то, что было нужно для длинных конечных строк».
Остин представил себе динамическую систему выдающей последовательность единиц и нулей. Если динамическая система — это подбрасывание монетки, то это легко себе представить: решка будет 1, а орёл — 0. Но любую динамическую систему можно использовать для генерации двоичной последовательности, просто разделив пространство, в котором она работает, на две (не обязательно равные) части.
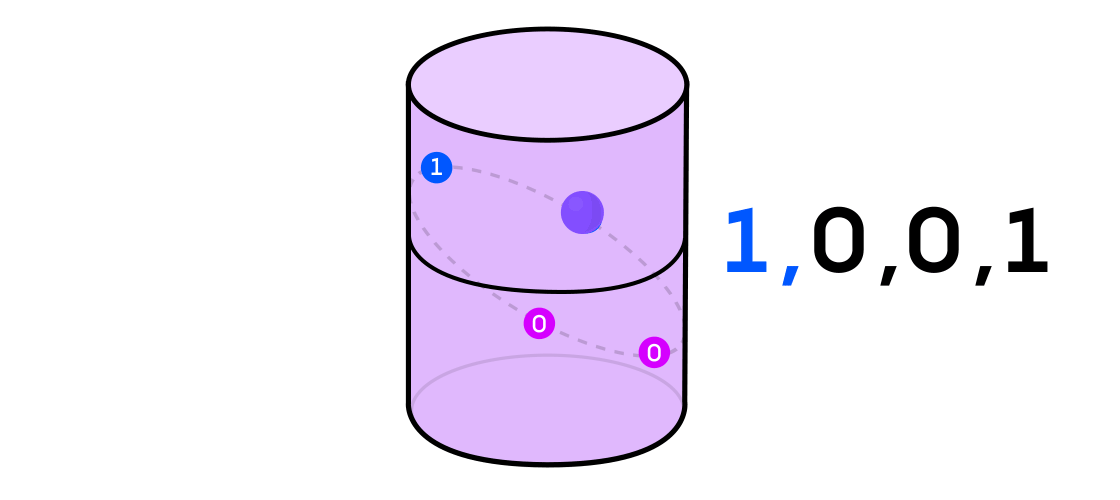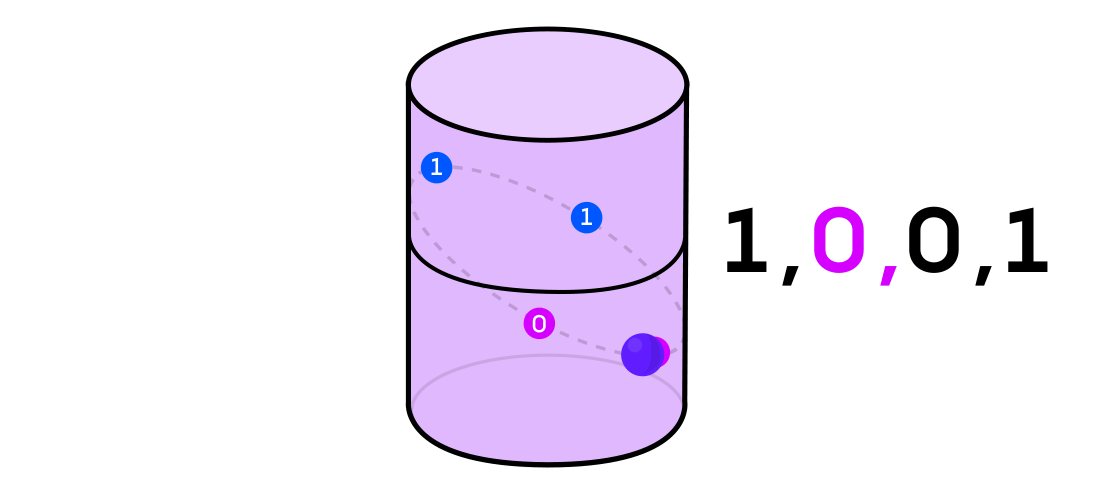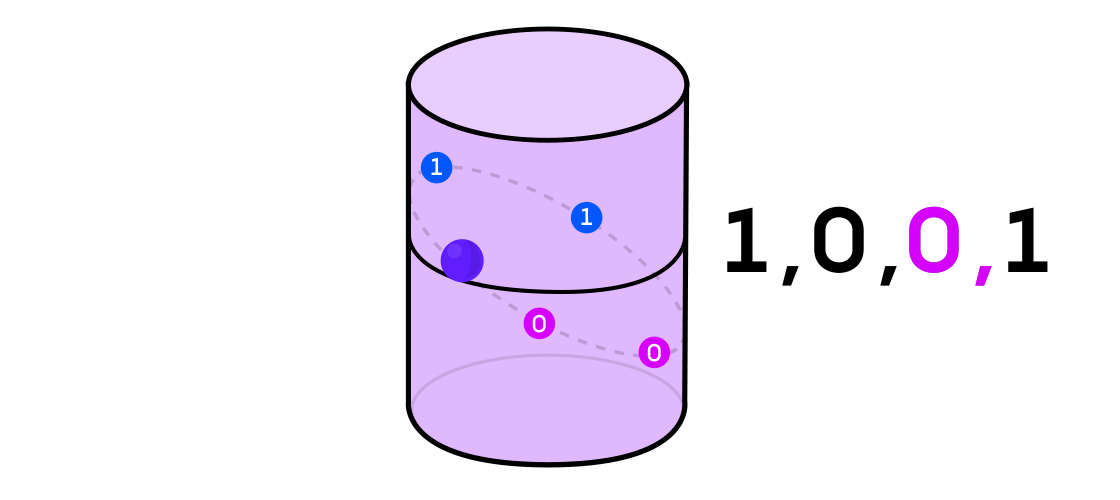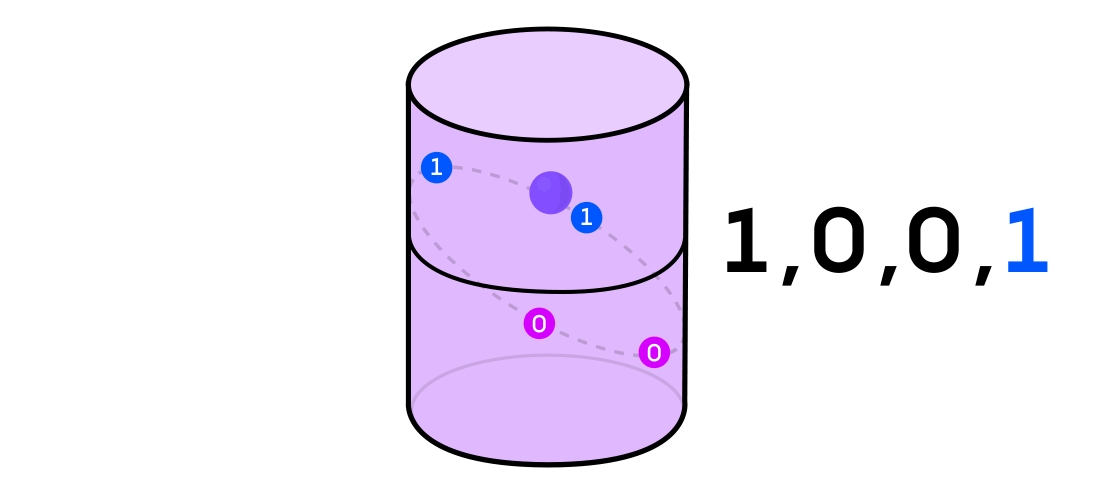
Возвращаясь к примеру динамической системы на цилиндре, если точка оказывается на одной части цилиндра, вы обозначаете выходное значение системы 1, а если на другой — то 0.
Остин проанализировал эти двоичные последовательности при помощи инструмента из теории информации под названием «кубы Хэмминга». Представьте куб из вершин, соединённых рёбрами. Каждой вершине назначают двоичные числа — допустим, 001 или 101. Каждый раз при переходе с одной вершины на другую меняется одна из трёх цифр.
Кубы Хэмминга могут быть гораздо сложнее, чем наш, у них может быть куда как больше рёбер и вершин в большем числе измерений, чем три –, но у всех них есть свойство, благодаря которому расстояние между двумя любыми вершинами — или количество рёбер, которые нужно пройти, чтобы перейти от одной вершины к другой — равно количеству мест, в которых различаются информационные строки, соответствующие этим вершинам. Поэтому 000 находится на расстоянии одного ребра от 001, двух рёбер от 011 и трёх от 111.

Чтобы изолировать случайные и детерминированные элементы, составляющие сложную динамическую систему, Остин думал о том, насколько часто динамическая система может выдавать заданную последовательность нулей и единиц, представленных на кубе Хэмминга. Он доказал, что эти последовательности распределены по кубу определённым образом. Они скапливаются в небольшом количестве подрегионов куба — и это скопление отражает детерминированность системы — однако распределены среди последовательностей в рамках этих кластеров случайным образом, что отражает случайность системы.
Такой окольный путь оказался необходимым для решения задачи, не поддававшейся прямым наскокам.
«Меня удивило не столько сама истинность или ложность слабой гипотезы Пинскера, сколько то, что её получилось доказать, поскольку эта задача казалась такой коварной, — сказал Льюис Боуэн, математик из Техасского университета в Остине. — До появления доказательства мы, по большому счёту, не представляли, можно ли вообще это сделать».
Результат Остина придаёт базовую структуру широкому спектру динамических систем. Математикам, которые часто вращаются среди объектов, которые кажутся взаимосвязанными, пусть и непонятно, каким образом, доказательство выдаёт их точную географию. Теперь у них есть путеводитель для этих динамических систем, хотя к каким именно открытиям это приведёт, пока неизвестно.
«Математиков всегда интересуют строительные блоки, из которых что-либо состоит, — сказала Линдси. — Доказательство Остина — отличный результат, которому, вероятно, найдётся множество применений в чистой математике, однако я не могу сказать, какими они будут».
