[Перевод] Наибольшие малые многогранники: новые решения в комбинаторной геометрии
Перевод поста Ed Pegg Jr.«Biggest Little Polyhedron—New Solutions in Combinatorial Geometry».Скачать файл, содержащий текст статьи, интерактивные модели многогранников и код, приведенный в статье, можно здесь.Выражаю огромную благодарность Кириллу Гузенко за помощь в переводе.
Во многих областях математики ответом будет единица 1. Возведение числа в квадрат, которое больше или меньше единицы, даст большее или меньшее число соответственно. Иногда для того, чтобы определить, является ли что-то «большим», необходимо выяснить, больше ли единицы наибольший размер этого объекта. К примеру, гигансткий гексагон Сатурна с длиной стороны в 13,800 км можно было-бы отнести к большим. «Малый многоугольник» — это тот, у которого максимальное расстояние между вершинами равно единице. В 1975 году Рон Грэм открыл наибольший малый шестиугольник, который, как показано ниже, имеет большую площадь, чем у правильного шестиугольника. Красные диагонали имеют единичную длину. Все остальные (непроведённые) диагонали имеют меньшую длину.
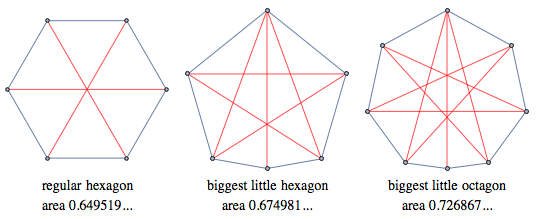Мне всегда было интересно, как будет выглядеть самый большой малый многогранник. В Mathematica 10 был представлен новый функциональный объект Volume[ConvexHullMesh[points]], и я подумал, что можно было бы решить эту задачу, выбирая случайные точки. Ниже представлен код для выбора, вычисления и визуализации случайного малого многогранника. Тысячи раз прокрутив этот код, можно будет получить неплохое приближение в лучшем из результатов. Вот, тут я три раза запускал код. Один из результатов, вероятно, лучше остальных.
Ниже на изображении приведены наилучшие решения, которые были получены через случайно выбранные точки. Я выложил это в Wolfram Community в обсуждении наибольший малый многогранник (далее — НММ) и получил несколько полезных комментариев от Робина Хьюстона и Тодда Роланда. Для поиска решений я решил использовать результаты «визуализации задачи Томпсона». В задаче Томсона электроны отталкиваются друг от друга на сфере. 12 отталкивающихся друг от друга точек стремятся к вершинам икосаэдра, что не эффективно для НММ, так как наибольшие расстояния проходят через центр сферы, так же как и для правильных шестиугольников в двумерном случае. Я изменил код для задачи Томпсона так, что точки отскакивали друг друга и ото всех противолежащих, и это дало неплохие начальные значения.
Для правильного тетраэдра с объёмом в 
/12= 0.117851 потребуется четыре точки.
Для правильной пирамиды с единичным перпендикуляром потребуется 5 точек, а её объём равен 
/12 = 0.1443375; это решение было получено в 1976-ом году [1].
Я буду использовать термин 6-НММ для обозначения наибольшего малого многогранника с шестью точками. В 2003-ем году объём 6-НММ был вычислен с точностью до четырёх знаков [2,3]. Ниже представлены 6-НММ и 7-НММ, единичные диагонали выделены красным.
Для того, чтобы найти их самостоятельно, сперва я выбрал наилучшие варианты из более чем тысячи, а затем использовал алгоритм имитации отжига (simulated annealing) (вероятностная задача поиска хорошего приближения к глобальному оптимуму данной функции в широком пространстве поиска — прим. пер.) для улучшения результатов. Для каждой из точек оптимальных решений я перебирал пространство вокруг этих точек для поиска лучшего решения, ненамного их смещая. Затем я ещё более уменьшал пространство поиска, и так из раза в раз. Некоторые из решений, казалось, стремятся к взаимной симметричности. К примеру, для семи точек лучшее решение стремилось к этому многограннику со значением r около половины, который представляет относительный размер верхнего треугольника △456.
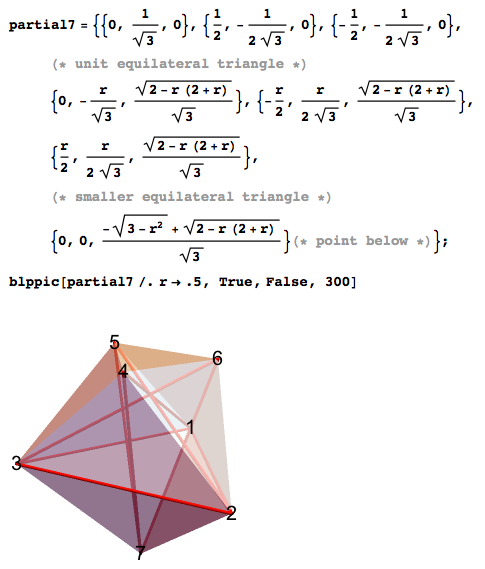
Точный объём можно получить через тетраэдр, который определяется через точки {{2,3,4,7}, {2,4,6,7}, {5,4,7,6}}, а объём первых двух следует утроить из соображений симметрии. Посмотрите на объёмы тетраэдров, и замените любую пару чисел в тетраэдре так, чтобы получился отрицательный объём.
После того, как мы изменили соотношение в последнем тетраэдре, мы можем вычислить точное значение r, которое даст точный и оптимальный объём. Этим же методом воспользуемся и для других случаев.
Решение для 16-НММ занимает более минуты, так что мне пришлось разбить его.
Первое значение в решениях — оптимальный объём, является объектом Root, а второе является оптимальным значением r. Вот, эта таблица будет поаккуратнее.
И это далеко за пределами того, что я смог бы сделать вручную. С помощью случайной выборки точек, алгоритма симуляции отжига, поиска симметрии, Solve[] и Maximize[] мне удалось найти точные значения объёмов n-НММ (наибольших малых многогранников) для n = 6, 7, 8, 9 и 16.
Вид 8-НММ с нескольких сторон, где красным выделены единичные диагонали.
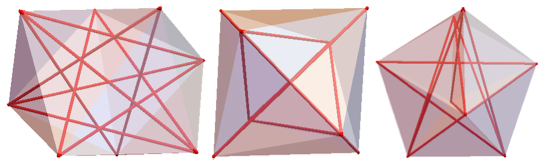
Вид 9-НММ с нескольких сторон:
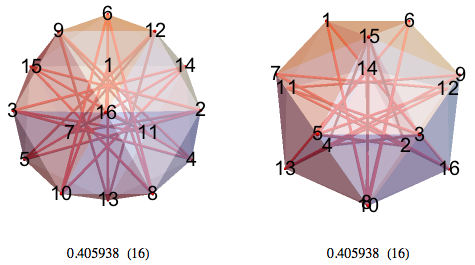
Вид 16-НММ с нескольких сторон:
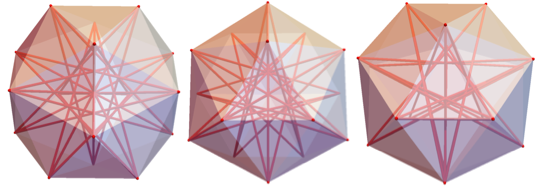
Указанный ниже 8-НММ содержит единичные перпендикуляры 1–2 и 3–4 над и под основанием соответственно. Представленный ниже 9-НММ содержит треугольники △123, △456 и △789.
Приведённый ниже 16-НММ представляет собой усечённый тетраэдр, состоящий из точек 1–12 с дополнительными точками 13–16.
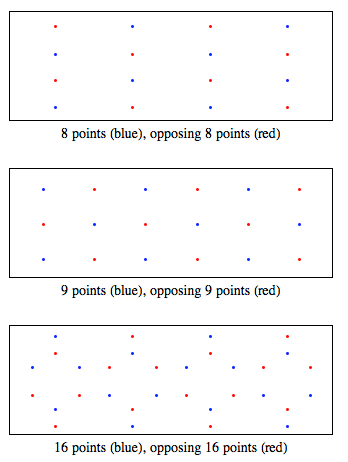
Довольно сложно, не так ли? С помощью метода выбора точек на сфере, случайными числами в промежутках [–Pi; Pi] и [–1; 1] на единичной сфере можно задать равномерное распределение точек. Точки на единичной сфере могут быть отображены обратно в точки в прямоугольнике [–Pi; Pi]x[–1; 1]. Вот, что произойдёт для решений 8,9,16-НММ.
Для 10-НММ мне не удалось найти точное решение, однако я могу представить численное решение с любой степенью точности. Свяжитесь со мной, если у Вас есть догадки, как тут найти root object. В исполняемой версии этой статьи на Wolfram Language в разделе инициализации можно найти это весьма нелёгкое выражение.
Тут представлены два вида 10-НММ с двух разных точек обзора.
Численное решение для 11-НММ можно найти схожим образом.
Вид 11-НММ с двух сторон:
Действительно ли я получил верные решения? Может быть и нет. Для этих симметрий я уверен, что я нашёл локальный максимум. Например, вот функция с локальным максимумом 5 при значении 1.
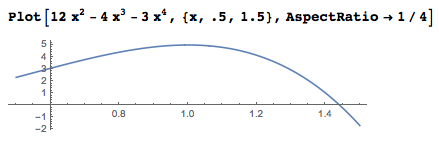
А если заглянуть в графике чуть дальше, то можно будет найти глобальный максимум 32 при значении в -2.
В схожей задаче Томпсона имеется доказательство для 12 вершин икосаэдра, находясь в которых система из 12 электронов находится в потенциальном минимуме. Но для 7, 8, 9, 10, 11 и 13+ электронов задача считается нерешённой. В гипотезе Кеплера предполагается, что гексагональная плотная упаковка есть плотнейшая упаковка для сфер, однако строгое доказательство было получено Томасом Хейлзом лишь 10-го августа 2014-го года. Плотнейшая упаковка для правильных тетраэдров — с отношением 4000/4671 = 0.856347… — была открыта лишь 27-го июля 2010-го года, однако до сих пор не имеет строгого доказательства. Любые заявления о найденном решении следует воспринимать с определённой долей скептицизма; геометрические задачи максимизации, как известно, очень сложны.
Несколько месяцев моё лучшее решение для 11 точек было в асимметричном локальном максимуме. Некоторые (или большинство) из этих решений, скорее всего, локальные, а не глобальные, но какие из них? С этой оговоркой можно посмотреть на самые известные решения для 12-ти и более точек.
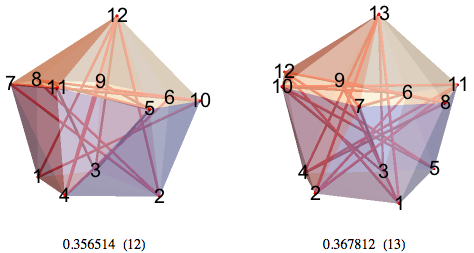
12-НММ имеет вершину в точке 12 и содержит в себе несколько кривоватый семиугольник 11–6–7–10–8–5–9 и четырёхугольник 1–4–3–2.
13-НММ имеет вершину в точке 13 и содержит в себе несколько кривоватый семиугольник 12–8–10–6–7–9–11 и такой же пятиугольник 1–2–3–4–5.
Мои попытки добавить симметрию привели к фигурам с меньшим объёмом.
По идее, решения для 14-НММ должны быть весьма симметричны, однако они у меня пока-что не получились. Я потратил некоторое время на оптимизацию системы вершина-пятиугольник-пятиугольник для 15-НММ, однако методом случайных точек было получено лучшее решение, в котором симметрия была принесена в жертву объёму.
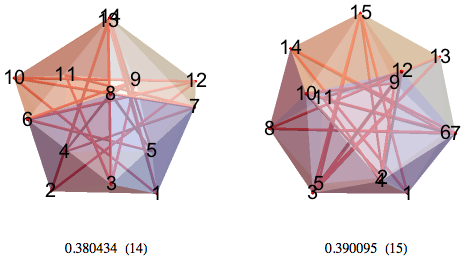
17-НММ, 18-НММ — я надеюсь, что в первом всё в порядке с симметрией.
Что касается 19-НММ и 20-НММ, то 20-НММ — не додекаэдр, так как единичные линии из центра — не лучший вариант.
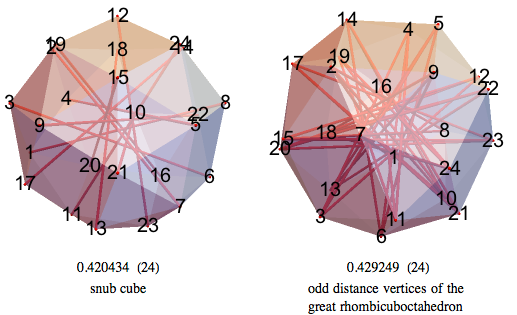
Как «курносый куб» (snub cube), так и половина огромного ромбокубоктаэдра — все имеют меньший объём, чем 24-НММ.
21-НММ и 22-НММ содержат множество семи- и девятиконечных звёзд.
23-НММ, 24-НММ — мой лучший 24-НММ имеет тетраэдрическую симметрию.
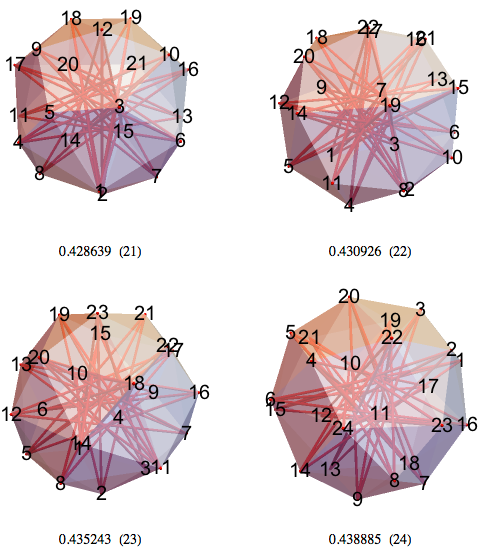
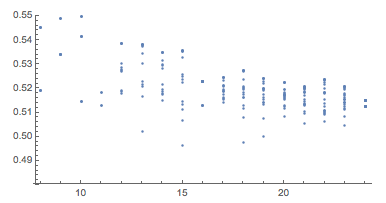
Вот некоторые симметрии в текущем лучшем 24-НММ. Отрезки 1–12 и 13–24 имеют соответствующие длины 0.512593 и 0.515168.
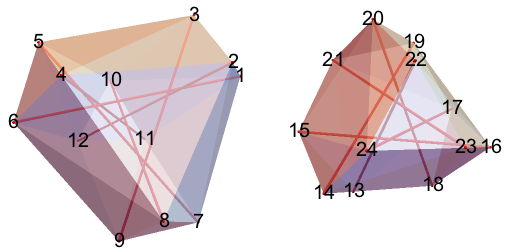
В 16-НММ и 17-НММ единичные отрезки определяют многоугольники. 16-НММ содержит множество семиконечных звёзд.
Ниже представлены те же самые многогранники, представленные как сплошные тела, посредством ConvexHullMesh[], для НММ 9–10–11–12, 13–14–15–16, 17–18–19–20, 21–22–23–24, соответственно.
Здесь представлена таблица наилучших известных на данный момент значений.
Вот лучшие решения, которые я нашёл на данный момент, для 4–24 точек.
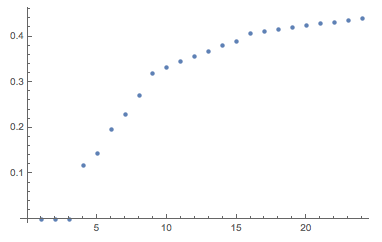
Пусть точки будут расположены так, чтобы максимальное расстояние от начала координат было как можно меньше. Распределение, представленное ниже, указывает на расстояния от начала координат до вершин каждого многогранника, в каждом из которых от 8 до 24 вершин.
С помощью Mathematica 10.1 удалось получить точные значения для 6,7,8,9-НММ и 16-НММ. Так же с её помощью были найдены очень точные, но численные значения для 10-НММ и 11-НММ и удалось серьёзно продвинуться с 24-НММ. Таким образом, мы получили решения семи ранее нерешённых задач в комбинаторной геометрии — все, благодаря комбинации Volume[ConvexHullMesh[points]]. А какие нововведения в Mathematica 10 помогли лично Вам?
Список литературы [1] B. Kind and P. Kleinschmidt, «On the Maximal Volume of Convex Bodies with Few Vertices,» Journal of Combinatorial Theory, Series A, 21(1) 1976 pp. 124–128.doi:10.1016/0097–3165(76)90056-X[2] A. Klein and M. Wessler, «The Largest Small n-dimensional Polytope with n+3 Vertices,» Journal of Combinatorial Theory, Series A, 102(2), 2003 pp. 401–409.doi:10.1016/S0097–3165(03)00054–2[3] A. Klein and M. Wessler, «A Correction to «The Largest Small n-dimensional Polytope with n+3 Vertices,» Journal of Combinatorial Theory, Series A, 112(1), 2005 pp. 173–174.doi:10.1016/j.jcta.2005.06.001
