[Перевод] Музыкальная теория для гиков
Кто-то считает музыку уделом избранных талантов, кто-то — набором физических закономерностей. Автор материала делает попытку объяснить знакомые каждому музыкальные термины, такие как тон, интервал, амплитуда, нота, октава, партитура, аккорд и так далее с помощью расчетов и технических обоснований. Ниже перевод оригинального текста.
Я ничего не знаю о музыке. Я знаю, что в музыке есть знаковые обозначения, но иногда у них вырастают закорючки. Я знаю, что увеличение октавы удваивает высоту звука. Я знаю, что для того, чтобы написать песню в стиле поп достаточно всего четырех аккордов. Вот, пожалуй, и все.
Все остальные правила для меня выглядят совершенно, ну просто абсолютно произвольно. Почему у нас есть 12 нот, но для их обозначения применяются только 7 букв? Откуда взялись знаки при ключе? Почему ни одну статью по музыке в Википедии просто невозможно понять, не прочитав сперва все остальные?
Несколько дней назад кое-что из всего этого, наконец, прояснилось. Я чувствую себя идиоткой из-за того, что не понимала этого раньше, но я полагаю, все дело в том, что все пытаются объяснить тебе музыку с использованием, кхм, музыкальной нотации, что едва ли имеет хоть какой-то смысл, пока вы не понимаете, почему все устроено именно так, а не иначе.
Здесь я расскажу вам о выводах, которые я сделала с позиции человека, чьи музыкальные уроки ограничились попыткой научиться играть 4 ноты с помощью магнитофона во втором классе. Подчеркну, что я ничего не знаю о музыке. Если вы умеете хотя бы свистеть, пожалуйста, не читайте этот пост, иначе будете надо мной смеяться.
Звуки и волны
Музыка — разновидность звука. Звук — это волна давления.
Представьте, что происходит, когда вы бьете в барабан. Когда вы бьете по нему, его мембрана, сделанная из упругого материала, деформируется сначала вовнутрь, а затем отскакивает наружу, потом снова вовнутрь и так далее до тех пор, пока не потеряет всю энергию. Если в этот момент вы будете наблюдать за точкой в центре мембраны, ее движение будет очень похоже на то, что получается, когда вы держите игрушечную шагающую пружинку (слинки) за один конец и отпускаете другой.
Когда мембрана отскакивает наружу, она выталкивает воздух перед собой. Этот воздух толкает еще больший объем воздуха у себя на пути, который повторяет то же действие с окружающими уже его воздушными молекулами, создавая трехмерную рябь, исходящую от барабана. Тем временем мембрана уже отскакивает вовнутрь, оставляя после себя вакуум, стремительно заполняемый окружающим воздухом, оставляющим за собой другой вакуум и так далее… В результаты молекулы воздуха вокруг барабана двигаются вперед назад по отношению к своему начальному положению, прямо как сама мембрана или пружина слинки.
В конечном счете волна давления достигает ваших барабанных перепонок, которые вибрируют таким же образом и вы интерпретируете эти колебания как музыку. Ну или как шум, в зависимости от ваших вкусов.
С радостью привела бы иллюстрацию этого процесса, но дело в том, что она выглядела бы как рябь на поверхности пруда, волны которой при этом двигаются вверх. Звуковые колебания происходят в трех измерениях, движение направляется вперед / от источника колебания, и это, на мой взгляд, очень важное отличие.
Так что вместо иллюстраций давайте лучше перейдем сразу к графикам и для начала взглянем на синусоидальную волну.

Неважно, что такое синусоидальная волна. Просто ее очень легко изображать на графике и поэтому удобно приводить в качестве типичного примера волны.
На графиках вроде этого время начинается с нуля и возрастает слева направо, а волна показывает насколько сильно воздух (или ваши перепонки, или другая среда) сдвинулась со своего начального положения. Полную тишину на этом графике можно отобразить в виде прямой линии, проходящей слева направо на уровне нуля.
Все звуки, которые вы когда-либо слышали, можно представить в виде такого же графика. Вот так вот просто. Если вы «откроете» песню в Audacity и приблизите график, вы увидите волну. Выглядеть она, скорее всего, будет несколько сложнее, но она по-прежнему будет волной.
Любую волну можно определить с помощью нескольких характеристик: частоты, амплитуды и формы. Всякий звук, который вы слышите, обладает некоторой формой, которая позволяет нам безошибочно различать звучание гитары и скрипки. Музыканты называют это свойство тембром.
Синусоидальная волна звучит примерно вот так:
Амплитуда — это расстояние между наивысшей и наинизшей точками волны. Ну или некоторые спецы определяют ее как половину этой величины, то есть расстояние между наивысшей точкой и нулем. Для нашего уха амплитуда — это громкость того или иного звука, что вполне логично, поскольку в терминах физики, амплитуда — наибольший численный показатель отклонения среды от начального состояния. Если стукнуть мембрану легонько, она отреагирует коротким колебанием, а звук будет тихим. Если же начать играть в полную силу, то колебания мембраны станут хорошо заметны, а барабан зазвучит гораздо громче.
Частота позволяет понять, насколько часто в буквальном смысле повторяется волна. Если волны на графике очень худые, тогда она повторяется чаще, то есть ее частота выше. Если гребни волны широкие, значит волна повторяется реже и ее частота ниже. Музыканты называют частоту высотой звука. Немузыканты, наверное, назовут ее просто нотой или тоном, что вызовет насмешки со стороны музыкантов, но что с них взять.
Частота измеряется в Гц (герцах). Это такая забавная замена словосочетанию «в секунду». Если на то, чтобы добраться из одной точки волны на графике в ту же самую точку следующий волны требуется полсекунды, то это 2 Гц, потому что за секунду по графику «пробегают» 2 волны. На приведенной выше записи вы слышали звук частотой 440 Гц. (Частота волны на графике, конечно же не такая. На нем изображена совершенно неизменная синусоидальная волна, сгенерированная wxMaxima, поэтому ее частота составляет 1/τ = 1/(2π)).
Важное свойство человеческого уха, определяющее многие другие музыкальные закономерности, заключается в том, что если вы увеличите или уменьшите частоту звука вдвое, то получившийся звук покажется вам в каком-то смысле «таким же». Очевидно, что вы будете воспринимать его как более высокий или более низкий, и тем не менее вы «почувствуете», что он очень похож на изначальный звук. Я конечно могу только догадываться о физической природе этого явления, но это правило так или иначе очень условно.
Сравните эти три синусоидальные волны, если хотите. Первая — это та же самая, изображенная ранее. Частота второй в 1.5 раза больше чем у первой, а у третьей частота увеличена вдвое. Первая и третья гораздо более близки друг другу по звучанию, нежели вторая по отношению к ним обоим.
Волна частотой 440 Hz
Волна частотой 660 Hz
Волна частотой 880 Hz
Ноты и октавы
Сложность с музыкальной теорией заключается в том, что только половина правил в ней имеет под собой логическое обоснование, но другая половина при этом весьма произвольна, и увидеть различие между этими двумя категориями с первого взгляда невозможно.
Давайте начнем со следующего факта о человеческих органах слуха: если прослушать сначала звук одной высоты, а потому удвоить его высоту (т. е. частоту), то второй вариант прозвучит для нас «так же» как и первый, но объяснить, откуда берется эта схожесть мы не можем. Таким образом, для любого начального тона f вы можете создать бесконечное количество других тонов, звучащих «также»: ½f, 2f, ¼f, 4f и так далее. Конечно, в диапазон восприятия человеческого уха попадет лишь некоторое, конечное их количество. Все эти тоны вместе взятые обладают неким общим качеством, поэтому давайте будем называть их группу нотой.
Нотой также можно назвать и отдельный тон. Введение такого понятия, как «класс тонов» устранило бы эту двусмысленность, но я все же буду и дальше применять термин «нота» как собирательный.
Если мы принимаем, что частота 440 Гц воспроизводит ноту под названием A, тогда 880 Гц, 220 Гц, 1760 Гц, 110 Гц и другие также будут соответствовать ноте под названием A. Отсюда следует важный вывод: диапазона частот 440 Гц и 880 Гц достаточно, чтобы определить все ноты, которые мы только можем придумать. Частоту любой другой высоты можно увеличивать или уменьшать вдвое до тех пор, пока полученное значение не попадет в этот диапазон и не станет соответствовать своей ноте в нем.
Подобный диапазон называется октавой. Почему он называется так мы увидим немного позже. Всякая нота может существовать только в пределах данной октавы, как бы вы ее ни называли. Например, самый нижний тон f — та же нота, что и 2f, который, таким образом, относится уже к следующей октаве.
И это хорошие новости! Это значит, что мы можем выбрать некую группу тонов, частоты которых лежат в пределах малого диапазона — любого малого диапазона размером f — 2f и увеличивать или уменьшать их частоты вдвое до тех пор, пока не получим стандартный набор нот, охватывающий весь диапазон человеческого слуха.
В связи с этим возникает другой вопрос: по какому правилу мы будем выбирать эти тоны? Вы можете предложить простой, на первый взгляд, подход. Например, взять все высоты от f до 2f с шагом 0.1f и получить последовательность f, 1.1f, 1.2f, 1.3f, 1.4f и так далее. Что может быть проще и понятнее равномерного шага?
Отличный план! К сожалению, на практике он работает не очень хорошо. Попробуйте сами и убедитесь, что разница в звучании между f и 1.1f — совсем не та же, что разница между 1.9f и 2f.
Человеческое ухо различает высоту звука на основании определенных пропорций (коэффициентов), что, в частности, объясняет и эффект удвоения или деления частоты пополам. Разница между f и 1.1f составляет 10%, тогда как 1.9f и 2f отличаются друг от друга всего лишь на ~5%.
То есть, выходит, нам нужен набор тонов, обладающих одинаковыми соотношениями звучания между друг другом, а не одинаковыми разницей в численном измерении. Если нам нужны n тонов, тогда нам требуется найти такое число, умножив которое n раз мы может пройти весь диапазон от f до 2f.
f × x × x × x × … × x = 2f
fxⁿ = 2f xⁿ = 2 x = ⁿ√2
Надо же. Нам нужен n-й корень из двух. Немного странно и необычно, потому что результат, так или иначе, окажется иррациональным для любого n > 1.
Интервалы в западной музыке
В западной музыке есть 12 различных тонов. Выбор этой величины в немалой степени произволен. То есть у двенадцати есть, конечно, несколько приятных математических свойств, но все ничего выдающегося в нем нет. Вы могли бы запросто придумать свой набор нот с 11-ю тонами, или 17-ю, или сотней или пятью. Что и делают некоторые другие музыкальные формы, используемые в других частях мира.
Коэффициент умножения между последовательными тонами в западной музыке, таким образом, равен корню 12-й степени из 2, или ¹²√2 ≈ 1.0594631. Взяв, например, частоту 440 Гц и последовательно умножая ее на этот коэффициент, мы получим 12 тонов, частота которых не превышает величину в 880 Гц.

На деле же никто не хочет работать с этими числами. Когда эта система придумывалась, никто про них просто не знал. Вместо этого на практике музыкальная терминология опирается на соотношения.
Соотношение между двумя тонами называется интервалом, а интервал размером корня 12-й степени из двух — полутоном. Использование интервалов позволяет выбросит все эти ужасные иррациональные числа куда подальше, а мы получаем возможность большую часть времени разговаривать на языке целых чисел.
На деле же мы работаем с логарифмической шкалой. По факту это всего лишь означает, что понятие «прибавить» превращается в «умножить».
А теперь вспомним, что человеческое ухо любит пропорции. Особенно ему милы пропорции, состоящие из небольших целых чисел, вот почему удвоение тона звучит «похоже»: в этом случае образуется соотношение 2 к 1, наименьшее из всех целочисленных, которое вы только сможете придумать.
Несмотря на тот факт, что корень 12-й степени из 2 — число иррациональное, оно тем не менее почти идеально подходит для создания нескольких замечательных пропорций. Не знаю почему именно 12 обладает таким эффектом, получается ли то же самое с какими-либо другими корнями, но это, вероятно, и есть та самая причина, по которой западная музыка остановилась на 12. Давайте приведем данные о тонах всех 12 нот и о том, как они соотносятся с первым тоном звукоряда. Некоторые из этих величин очень близки к правильным дробям.

Не считая октавы, мы получаем семь приятных на вид дробей.
Хм. Семь. Какое примечательное число.
Гаммы
Сюрприз! Это приятные на вид соотношения образуют мажорную гамму. Если начать с ноты C (то есть до), мы получим хорошо знакомые нам «натуральные» ноты, образующие гамму до мажор (C major). Используя знак ♯ (так называемый диез), который означает «повышение на один полутон», и ♭ (так называемый бемоль), то есть «понижение на один полутон», мы можем обозначить и все остальные ноты.

Не знаю наверняка, но я точно не удивлюсь, если узнаю, что именно такая логика, которую я здесь описала, и привела к появлению современной системы именования звуков.
Теперь вы можете видеть, откуда взялись названия некоторых интервалов. Чистая квинта (лат. quinta — пятая) — интервал между первой и пятой нотами гаммы. Октава от (лат. Octava — восьмая) охватывает в общей сложности восемь нот. Точно так же самый малый интервал получил название полутона, поскольку расстояние между большинством нот было названо целым тоном, а сами они находятся в двух шагах друг от друга.
Интервалы между следующими друг за другом нотами могут быть записаны в виде тон-тон-полутон-тон-тон-тон-полутон. Поскольку октавы повторяются по кругу, вы можете создавать семь разных вариаций, выбирая в качестве начала последовательности любую из семи нот. Полученные таким образом гаммы называются диатоническими, а выбор начальной позиции получил название лада или тональности. Приведу здесь все семь вариантов. Римские цифры указывают на порядковый номер ступени С-мажора, принятой за первую в том или ином столбце. Полученные в итоге ноты выглядят «натурально».

Обратите внимание, что два столбца выделены. В столбце номер I вы видите мажорный звукоряд (гамма), а в столбце VI — натуральный минорный звукоряд (гамма). Теперь мы можем объяснить и происхождение названий остальных интервалов: малая (minor, англ.) терция — промежуток между первой и третьими нотами минорной гаммы, тогда как большая (major, англ.) терция — промежуток между первой и третьими нотами в гамме мажорной. Что касается четвертой и пятой нот, то расстояние между ними и первой нотой в обоих видах гамм одинаково.
(То же самое и с интервалом между второй и первой нотами, и поэтому происхождение «малой (minor, англ.) секунды» мне ясно).
Чтобы создать мажорную или минорную гамму, вы можете начать с любой ноты. Важно лишь сохранять тот же рисунок интервалов. Наличие 12 нот позволяет создать в общей сложности двадцать четыре мажорные и минорные гаммы, которых хватит на целую большую и скучную диаграмму. Приведу вам несколько других мажорных гамм.

Если «повернуть по кругу» эти мажорные гаммы так, чтобы они начинались с C, они будут выглядеть так:

А вот несколько минорных гамм, записанных в том же виде:

Так так, что мы видим? Да, каждая мажорная гамма эквивалентна минорной, если начинать отсчет с предпоследней ноты. Такие гаммы приходятся друг другу параллельным мажором и параллельным минором.
А еще у этой нотации одна маленькая проблема. Она заключается в том, что записанная в партитурах музыка просто ужасна.
Партитура и ключевые знаки
Если вы знаете что-нибудь о нотном письме, вы наверняка заметили, что под запись бемолей и диезов не отводится никакого определенного места.
То есть если вы хотите добавить другие, повышенные или пониженные ноты, вы делаете это на той же линейке, но с ♯ или ♭ рядом с ними. Поэтому ноты из D мажора, в числе которых есть F♯ и C♯ пишутся на той же линейке, что и просто F или C, но с добавлением ♯, брошенного прямо перед ними. Дописывать этот знак каждый раз не очень удобно, поэтому вы можете поставить его в виде знака при ключе в самом начале. Такая запись выглядит как несколько ♯ или ♭, записанных в определенных местах с целью указания на то, какие ноты следует повышать или понижать. После этого всякая, не украшенная подобным обозначением нота, будет считаться повышенной или пониженной по умолчанию.
А сами ноты могут изображаются далеко не только так, как показано выше. У них к тому же бывают закорючки, которые могут соединять их с другими нотами сверху или снизу, что отчасти зависит еще и от того, как были нарисованы соседние ноты.
Что ж… Полагаю… это удобно? Если ваша музыка почти полностью основывается на применении семи нот определенной гаммы, тогда будет компактнее иметь партитуру, рассчитанную только на 7 нот и подстраивать их обозначение под эту систему, когда понадобится… да?
Однако такой подход совершенно опровергает соотношение между тонами. Глядя на некоторые партитуры, вы не сможете даже с легкостью сказать, в какой тональности они написаны, не говоря уже о том, чтобы выучить все это наизусть. В приведенном выше примере присутствуют ♯ для C и F. Однако как именно, глядя на это обозначение, вы должны понять, что речь идет о тональности «D мажор»?
Так или иначе, я затронула эту тему только для того, чтобы обратить ваше внимание на систему нотации. Давайте снова взглянем на C♯ мажор:

Получается, что две пары нот используют одинаковое буквенное обозначение — C и C♯, F и F♯ и занимают поэтому одну и ту же линейку в партитуре. Описанная мною только что схема добавления знаков при ключе не позволяет так делать.
Чтобы исправить эту ситуацию, композиторы прибегают к небольшой уловке. C находится на полтона выше B, поэтому ее можно также записать как B♯. F находится на полтона выше E, поэтому вместо F вы также можете писать E♯. То есть вот так C♯ будет выглядеть в итоге:

Благодаря этому все семь букв будут использоваться в ней только один раз.
Я не думаю, что до конца понимаю смысл этого подхода, потому что он кажется мне слишком изощренным. То есть вам нужно в уме превратить C в C♯, а после этого еще и перевести C♯ в ту ноту, которая на самом деле играется на вашем инструменте в данном случае. Чего пытались добиться авторы этого метода? Пожалуй, единственное разумное объяснение этому, которое приходит мне в голову, заключается в желании сохранить компактность партитурной записи и уложиться ровно в 7 нот.
Полагаю, что поменяв ключевые знаки, можно изменить звучание всего музыкального произведения. Иногда этого вполне достаточно, то есть после этого действия вам вообще не придется выполнять какие-либо дополнительные манипуляции. Интересно, как это отразится на музыке, в которой также применяются ноты, выходящие за рамки используемой гаммы? Впрочем, это уже скорее вопрос композиции, в которой я совершенно точно ничего не понимаю.
Что-то там, что-то там и аккорды
Начнем потихоньку выбираться из дебрей.
Как я и говорила, мажорные и минорные гаммы «ходят парой»: каждая мажорная гамма имеет «родственную» минорную, обладающую совершенно одинаковым набором нот и наоборот. Так, C мажор идентична А минор. Зачем нам сразу две одинаковые гаммы? И что еще важнее, как мы вообще можем сказать, какая из них используется в том или ином музыкальном произведении, если у них обоих одинаковый набор знаков при ключе?
Многие люди пытались объяснить мне, что параллельные гаммы отличаются настроением, у них разное звучание и много еще чего такого, но все эти аргументы скорее создают новые вопросы, чем отвечают на уже заданные. Я пришла к выводу, что правильный ответ состоит из двух частей.
Первая часть. При написании музыки композитор отталкивается от ключа, который включает в себя как гамму, так и типовые аккорды, а кроме того и много еще чего другого. Аккорд — это несколько нот, звучащих одновременно или почти одновременно. Вы можете создать множество разных аккордов, однако самые популярные из них — мажорные аккорды и минорные аккорды, которые состоят из первой, третьей и пятой нот гаммы. Аккорд C мажор (который часто по непонятной причине записывают просто как C), таким образом, состоит из C, E и G, тогда как аккорд A минор (записывается как Am) — из A, C и E.
Мажорные аккорды состоят из какого-либо основного тона, и двух нот, отстоящих от него на 4 и на 7 полутонов вверх, или, если еще проще, то {0, 4, 7}. Минорные аккорды имеют вид {0, 3, 7}. Первые и последние ноты в обоих видах аккордов отделены друг от друга 7 полутонами, то есть чистой квинтой — тем самым приятным соотношением 3:2. Мажорные и минорные аккорды с одинаковым основным тоном похожи по звучанию, однако слегка пониженная средняя нота минорного аккорда делает его звучание несколько более драматичным или угрюмым.
Кстати, если вы сравните мажорную и минорную гаммы, начинающиеся с одной и той же ноты, вы заметите кое-что интересное. Они очень похожи друг на друга, за исключением того, что в мажоре три ноты звучат на полтона выше.

Для каждой мажорной и минорной гаммы можно составить семь аккордов такой формы, по одному на каждую ноту. К примеру второй аккорд в гамме C мажор — это группа нот D-F-A, или просто D минор. Да, именно минор. Это тот же порядок нот, что и в первом аккорде гаммы D минор.
Иногда вы встретите аккорды, записанные с помощью римских цифр. В таких случаях прописные (большие) символы применяются для обозначения нот, из которых состоят мажорные аккорды данной тональности, а строчные (малые) — для минорных. Аккорды мажорной гаммы записываются в виде I, ii, iii, IV, V, vi, и vii, аккорды минорной гаммы — i, ii, III, iv, v, VI, and VII. Цифра «I» всего лишь означает, что аккорд строится от первой ноты гаммы и так далее. Эта система обозначений позволяет говорить, например, об аккордовых последовательностях, не беспокоясь при этом о знаках при ключе.
Так или иначе, возвращаясь к вопросу о том, почему мы используем как A минор, так и C мажор, мы подошли ко…
Второй части ответа. Это просто обычай. В западной музыке наблюдается тенденция писать произведения согласно некоторым общепринятым нормам и хорошо разбирающиеся в них люди могут распознать о какой именно гамме идет речь в том или ином случае. Записанная в C мажоре музыка будет часто начинаться с C или заканчиваться на эту ноту или даже аккорд C мажор. Музыка, написанная в A минор, нередко будет начинаться с A или заканчиваться на эту ноту или аккорд A минор.
Полагаю, что преимущество этого подхода такое же, как и в случае с любыми другими общепринятыми нормами: ваша работа будет более доступна для других людей из вашей сферы деятельности. Транспонирование музыки из одного ключа в другой, к примеру, по-настоящему имеет смысл, только если вы можете с уверенностью сказать, какой ключевые знаки использовались изначально. Кстати, недавно мне скинули интересную ссылку на исполнение Für Elise в А мажоре, вместо A минора, в котором она изначально была написана.
А если бы вы сыграли ее в С мажоре, она прозвучала бы как… э… стоп, я запуталась.
Разумеется, не стоит удивляться тому, что эта общепринятая норма проявляет себя в огромном количестве самых разных нюансов. Например, существует гармоническая минорная гамма, седьмая нота в которой приподнята вверх на полтона. В мелодической минорной гамме корректировки вносятся сразу в несколько нот, но только в восходящем порядке, а не в нисходящем. Существуют и увеличенные аккорды (и интервалы), самые высокие ноты которых поднимаются на полутон, и уменьшенные аккорды (и интервалы), самые высокие ноты которых, напротив, понижаются на полутон. И еще много всякого такого. Все эти нюансы довольно-таки беспорядочно наслаиваются друг на друга и создают множество конфликтующих названий для одних и тех же понятий. Сами они при этом больше похоже на попытки описать человеческие намерения, нежели объективную форму звуковых колебаний.
Есть такая штука под названием «квинтовый круг», которая представляет собой графическое отображение всех мажорных и минорных гамм, где они расположены по кругу. Оказывается, что если вы назовете их и расположите в правильном порядке, каждая гамма будет обладать разным количеством диезов и бемолей. При этом вы не найдете ни одной гаммы, которая применяла бы как диезы, так и бемоли одновременно. Под «правильным порядком» подразумевается последовательная попарная запись первых нот параллельных мажорной и минорной тональностей. Расстояние между каждой парой при этом составляет 7 полутонов (отсюда и слово «квинта» в названии). Диезы или бемоли используются в тех или иных тональностях в зависимости от того, какой символ позволит всем их звукам «вписаться» в 7-ми буквенную систему без повторений и таким образом сделать так, чтобы на партитуре все выглядело компактно и приятно. Я уверена, что модульная арифметика может объяснить, почему все это так хорошо работает на практике, но не могу предоставить его вот так сразу.
Ах да, что касается целочисленных соотношений, то они, не зря так нравятся человеческому уху, поскольку влияют в том числе на периодическую стройность суммарных волн. Вот как выглядит чистая квинта. Двое звуков сверху — это A4 и E5, использующие не совсем идеальный корень 12-й степени из двух. Однако благодаря тому факту, что соотношение между ними составляет весьма приятную величину 3:2, их совмещение создает повторяющуюся последовательность из 6 волн, которая сама по себе напоминает волну.
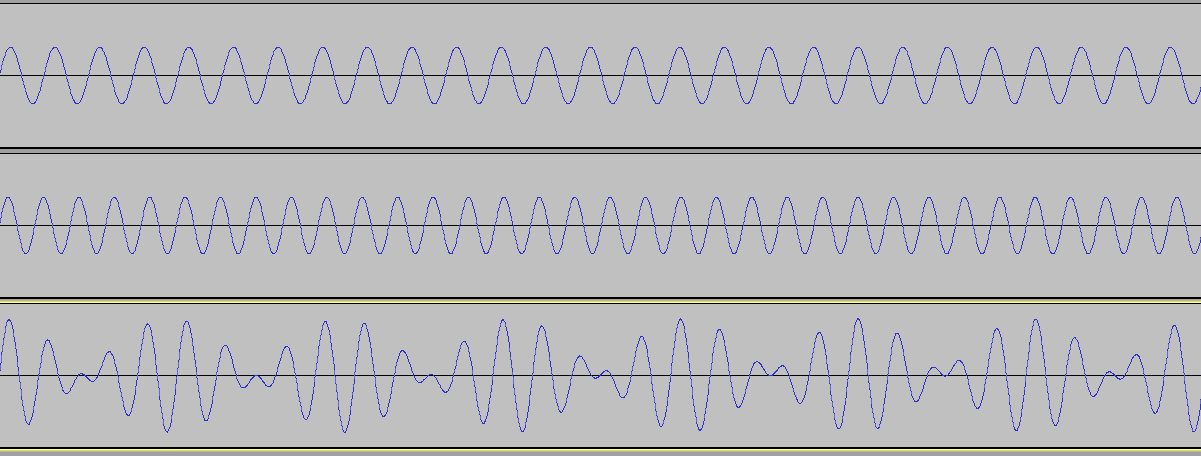
A4 — нота A четвертой октавы. Четвертая октава начинается с С, расположенной в середине клавиатуры фортепиано. A четвертой октавы имеет частоту 440 Гц и эта величина используется в качестве общепринятого звукового ориентира для настройки инструментов.
И, наконец, ноты с «одинаковым названием» могут на самом деле звучать по-разному, в зависимости от настройки отдельно взятого инструмента. Различные применяемые сегодня схемы настройки основываются на точных целочисленных отношениях, а не приблизительных. А еще, помимо E♯ существуют также и другие «липовые» ноты. Ходят слухи, что существует в музыке и такая дичь, как нота G♯ или «G-дубль-диез», которую я бы скорее назвал просто A. Подозреваю, что два этих явления как-то связаны, но вот только точно не знаю как.
Вот и все, что я знаю. Больше я на эту тему ничего рассказать не могу.
В заключение
Музыкальная нотация — худшая из всех систем обозначения или жаргонов, с которыми я когда-либо сталкивалась.
Я занялась изучением всего этого только потому, что хотела сочинить немного своей музыки и почувствовала себя абсолютно бессильной, поскольку вообще не поняла эту систему. Не уверена, оказалось ли полезным для меня, все что я здесь описала, но по крайней мере теперь эта тема не вызывает у меня откровенного недоумения.
Мне кажется вообще все в этом предмете, что нельзя выразить в виде чистой математики или волновой теории в высшей степени условно. Вы можете выбрать любой набор из 12 нот, какой только пожелаете и создать с их помощью музыку. Один из моих собеседников как-то отметил, что если вы будете использовать только черные клавиши фортепиано (то есть не натуральные ноты), получится пентатоника, сочинять в которой можно вообще почти все что угодно, не боясь получить ужасное звучание, поскольку интервал между каждой парой нот в ней составляет как минимум целый тон. Вы также можете использовать высоты, не входящие в набор из 12 нот, как это делают многие джазовые, незападные и другие, действующие вне рамок классической школы, музыканты.
У меня возникает чувство, что любые попытки относиться ко всей этой системе ключей или аккордов, как к единому набору правил можно сравнить с изучением живописи эпохи Возрождения и желанием решить, что именно это и есть настоящее искусство. Но это не так. Делайте, что хотите, главное чтобы звучало хорошо. Именно этим я и займусь. Для себя я решила, что истинная сущность музыки, как и всякой формы искусства, заключается в умении правильно изобразить контрасты.
Если же вы, в отличие от меня, еще не готовы забросить западную музыкальную традицию, вот вам немного полезных ссылок, которые люди давали мне, пока я пыталась разобраться во всем этом в режиме реального времени в своем твиттере.
- This Week«s Finds in Mathematical Physics — математика музыки на основе теории групп.
- Music — урок от Тоби Фокса, создателя саундтрека к Undertale, да и вообще всего Undertale.
- Musimathics: The Mathematical Foundations of Music — книга за 33 доллара, рекомендованная мне несколько раз, но так пока что мной и не купленная.
- How Music Really Works — книга, которая прямо с обложки хвастается, что в ней нет никакой музыкальной нотации и предлагает первые 6 глав бесплатно. Обзоры к ней говорят о том, что она особенно полезна для сочинения музыки, так что, возможно, ее стоит почитать.
- Combinatorial Music Theory — попытка описать теории музыки. По всей видимости, ее автор — математик, который забыл как объяснять что-либо без применения сложных математических понятий.
- The Geometry of Musical Rhythm: What Makes a «Good» Rhythm Good? — книга, название которой полностью передает суть ее содержимого.
- An answer from the music Stack Exchange предпринимает попытки разобраться почему музыкальная теория такая, какой мы ее знаем.
- A Geometry of Music рекомендована в предыдущем ответе со Stack Exchange в качестве лучшего варианта для новичка.
