[Перевод] Логика, объяснимость и будущее понимания
Открытие, связанное с логикой
Логика служит основой множества вещей. Но каковы основы самой логики?
В символьной логике вводятся символы вроде p и q, обозначающие утверждения (или «пропозиции») типа «это интересное эссе». Ещё есть определённые правила логики, к примеру, для любого p и любого q выражение NOT (p AND q) аналогично (NOT p) OR (NOT q).
Но откуда берутся эти «правила логики»? Логика — система формальная. Как и евклидову геометрию, её можно построить на аксиомах. Но что такое аксиомы? Можно начать с таких утверждений, как p AND q = q AND p, или NOT NOT p = p. Но сколько аксиом требуется? Насколько они могут быть простыми?
Этот вопрос довольно давно был мучительным. Но в 20:31 в воскресенье, 29 января 2000 года, на экране моего компьютера появилась единственная аксиома. Я уже показал, что проще ничего быть не может, но вскоре установил, что этой единственной небольшой аксиомы было достаточно, чтобы создать всю логику:
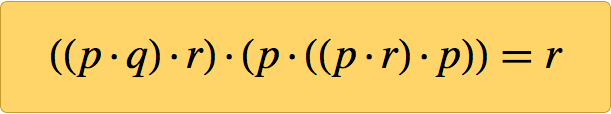
Откуда мне было знать, что она верна? Потому что я заставил компьютер доказать её. И вот доказательство, распечатанное мною в книге «Новый тип науки» (уже доступной в репозитории Wolfram Data):

Используя последнюю версию Wolfram Language любой способен сгенерировать это доказательство не более, чем за минуту. И каждый его шаг легко проверить. Но почему результат будет верным? Как его объяснить?
Подобные вопросы всё чаще задают по поводу всяческих вычислительных систем и приложений, связанных с машинным обучением и ИИ. Да, мы видим, что происходит. Но можем ли мы это понять?
Я думаю, что этот вопрос глубок по своей сути — и критически важен для будущего науки и технологии, и для будущего всего интеллектуального развития.
Но перед тем, как мы будем говорить об этом, давайте обсудим аксиому, обнаруженную мною.
История
Логика как формальная дисциплина происходит от Аристотеля, жившего в 4-м веке до нашей эры. В рамках работы своей жизни по каталогизации вещей (животных, причин, и т.п.) Аристотель составлял каталог допустимых форм аргументов и создавал символические шаблоны для них, которые, по сути, обеспечили главное содержание логики на две тысячи лет вперёд.
Однако к XV веку изобрели алгебру, а с ней появилось более ясное представление вещей. Но только в 1847 году Джордж Буль, наконец, сформулировал логику так же, как алгебру, с логическими операциями типа AND и OR, работающими по правилам, похожим на правила алгебры.
Через несколько лет люди уже записывали аксиоматические системы для логики. Типичным примером было:
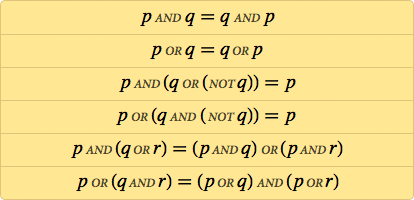
Но нужны ли на самом деле для логики AND, OR и NOT? После первого десятилетия XX века несколько людей обнаружили, что достаточно будет единственной операции, которую мы теперь называем NAND, и, к примеру, p OR q можно вычислить, как (p NAND p) NAND (q NAND q). «Функциональная полнота» NAND могла навеки остаться диковиной, если бы не разработка полупроводниковой технологии — она реализует все миллиарды логических операций в современном микропроцессоре при помощи комбинации транзисторов, выполняющих лишь функцию NAND или связанную с ней NOR.
Ну хорошо, так как же выглядят аксиомы логики в терминах NAND? Вот первый известный их вариант, записанный Генри Шеффером в 1913 году (здесь точка обозначает NAND):
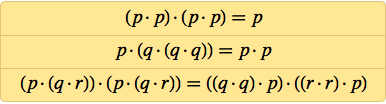
В 1910-м Principia Mathematica, трёхтомный труд по логике и философии математики Альфреда Норта Уайтхеда и Бертрана Рассела, популяризовал идею о том, что, возможно, всю математику можно вывести из логики. Учитывая это, довольно интересно было изучить вопрос того, насколько простыми могут быть аксиомы логики. Наиболее значимые работы в этой области проводили во Львове и Варшаве (тогда эти города были в составе Польши), в частности, Ян Лукасевич (в качестве побочного эффекта своей работы в 1920-м изобрёл «польскую» запись, не требующую скобок). В 1944 году в возрасте 66 лет Лукасевич бежал от наступающей советской армии и в 1947-м оказался в Ирландии.
Тем временем ирландец Кэрью Мередит, учившийся в Винчестере и Кембридже, и ставший преподавателем математики в Кембридже, из-за своего пацифизма был вынужден вернуться в Ирландию в 1939-м. В 1947-м Мередит попал на лекцию Лукасевича в Дублине, что вдохновило его заняться поисками простых аксиом, чем он и занимался, по большей части, всю оставшуюся жизнь.
Уже к 1949 Мередит обнаружил двухаксиомную систему:
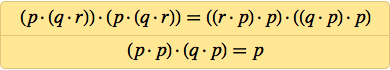
Почти 20 лет работы спустя, в 1967 ему удалось упростить это до:
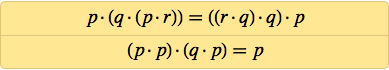
А можно ли упростить это и далее? Мередит годами возился с этим, выясняя, где ещё можно убрать лишние NAND. Но после 1967-го дальше он уже не продвинулся (и умер в 1976), хотя в 1969-м он нашёл трёхаксиомную систему:
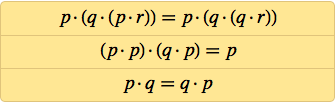
Когда я начал изучать аксиомные системы логики, я ничего не знал о работе Мередита. Я увлёкся этой темой в рамках попыток понять, какое поведение может вырастать из простых правил. В 1980-х я сделал неожиданное открытие, что даже клеточные автоматы с простейшими из возможных правил — таких, как моё любимое правило 30 — могут приводить к невероятно сложному поведению.
Проведя 1990-е в попытках понять общность этого явления, я в итоге захотел посмотреть, как его можно применить к математике. В математике мы, по сути, начинаем работать с аксиом (допустим, в арифметике, в геометрии, в логике), а потом на их основе пытаемся доказать целый набор сложных теорем.
Однако насколько простыми могут быть аксиомы? Именно это я хотел установить в 1999-м. В качестве первого примера я решил изучить логику (или, что то же самое, булеву алгебру). Опровергая все мои ожидания, мой опыт с клеточными автоматами, машинами Тьюринга и другими системами — включая даже дифференциальные уравнения в частных производных — говорит о том, что можно просто начать перечислять наиболее простые случаи из возможных, и в какой-то момент увидеть кое-что интересное.
Но можно ли таким способом «открыть логику»? Был лишь один способ сказать это. И в конце 1999 я устроил всё так, чтобы начать изучать пространство всех возможных систем аксиом, начиная с самых простых.
В каком-то смысле, любая система аксиом задаёт набор ограничений, допустим, на p · q. Она не говорит, что такое p · q, она только даёт свойства, которым должно удовлетворять p · q (к примеру, она может заявить, что q · p = p · q). Тогда вопрос в том, можно ли из этих свойств вывести все теоремы логики, выполняющиеся, когда p · q является Nand[p, q]: ни больше, ни меньше.
Кое-что можно проверить напрямую. Можно взять систему аксиом и посмотреть, какие формы p · q удовлетворяют аксиомам, если p и q будут, допустим, означать true и false. Если система аксиом состоит в том, что q · p = p · q, тогда да, p · q могут быть Nand[p, q] –, но не обязательно. Оно может также быть And[p, q] или Equal[p, q], или ещё многими другими вариантами, не удовлетворяющими тех же самых уровней, как функция NAND в логике. Но к тому времени, когда мы доходим до системы аксиом {((p · p) · q) · (q · p) = q}, мы доходим до состояния, в котором Nand[p, q] (и эквивалент Nor[p, q]) остаются единственными работающими моделями p · q — по крайней мере, если предположить, что у q и p бывает только два возможных значения.
Является ли тогда это системой аксиом для логики? Нет. Потому что оно подразумевает, к примеру, существование варианта, когда у p и q есть три значения, а в логике такого нет. Однако тот факт, что эта система аксиом из одной аксиомы близко подходит к тому, что нам нужно, говорит о том, что стоит поискать единую аксиому, из которой воспроизводится логика. Именно это я и сделал в январе 2000 (в наше время эта задача облегчилась, благодаря достаточно новой и очень удобной функции Wolfram Language, Groupings).
Было довольно легко проверить, что аксиомы, в которых было 3 или меньше NAND (или «оператора точка») не работали. К 5 утра в воскресенье, 29 января (ага, тогда я был совой), я обнаружил, что не сработают и аксиомы, содержащие 4 NAND. Когда я прекратил работу, примерно к 6 утра, у меня на руках было 14 кандидатов с пятью NAND. Но продолжив работу вечером в воскресенье и проведя дополнительные испытания, пришлось отбросить их все.
Незачем и говорить, что следующим шагом стала проверка аксиом с 6 NAND. Их оказалось 288 684. Но мой код работал эффективно, и прошло не так много времени перед тем, как на экране появилось следующее (да, из Mathematica Version 4):

Сначала я не понял, что у меня получилось. Я только знал, что у меня есть 25 неэквивалентных аксиом с 6 NAND, которым удалось продвинуться дальше, чем аксиомам с 5 NAND. Но были ли среди них аксиомы, порождающие логику? У меня был эмпирический метод, способный отбрасывать ненужные аксиомы. Но единственным способом точно узнать правильность конкретной аксиомы было доказать, что она успешно способна воспроизвести, допустим, аксиомы Шеффера для логики.
Потребовалось немного поиграться с программами, но по прошествии нескольких дней я обнаружил, что большая часть из полученных 25 аксиом не работает. В итоге выжили две:
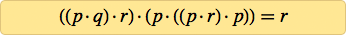

И к моей великой радости, я сумел при помощи компьютера доказать, что обе являются аксиомами для логики. Использованная техника гарантировала отсутствие более простых аксиом для логики. Поэтому я знал, что пришёл к цели: после века (а может, и пары тысячелетий) поисков мы, наконец, можем заявить, что нашли простейшую аксиому для логики.
Вскоре после этого я обнаружил системы из двух аксиом с 6 NAND в целом, которыке, как я доказал, способны воспроизводить логику:
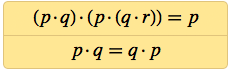
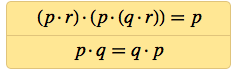
А если принять коммутативность p · q = q · p, как само собой разумеющееся, тогда логику можно получить из аксиомы, содержащей всего 4 NAND.
Почему это важно
Ладно, допустим, очень прикольно иметь возможность сказать, что кто-то «завершил дело, начатое Аристотелем» (или хотя бы Булем) и обнаружил простейшую из возможных систему аксиом для логики. Это просто диковинка, или у данного факта есть важные последствия?
До платформы, разработанной мною в книге A New Kind of Science, думаю, было бы сложно считать этот факт чем-то большим, чем просто диковинка. Но теперь должно быть видно, что он связан со всяческими базовыми вопросами, вроде того, нужно ли считать математику открытием или изобретением.
Та математика, которой занимаются люди, основана на горстке определённых систем аксиом — каждая из которых определяет особую область математики (логика, теория групп, геометрия, теория множеств). Но говоря абстрактно, есть бесконечное множество систем аксиом — каждая из которых определяет область математики, которую можно изучать, даже если люди ещё этим не занимались.
До книги A New Kind of Science я, видимо, подразумевал, что всё, существующее «где-то там» в вычислительной вселенной, должно быть «менее интересным» чем то, что люди создали и изучили. Но мои открытия, касающиеся простых программ, указывают что в системах, которые просто «где-то там» существуют, скрыты не менее богатые возможности, чем в системах, тщательно отобранных людьми.
Так что насчёт системы аксиом для математики? Чтобы сравнить существующее «где-то там» с тем, что изучали люди, нужно знать, лгут ли системы аксиом для существующих областей математики, изученных нами. И, основываясь на традиционных системах, созданных людьми, можно заключить, что они должны быть где-то очень, очень далеко — и вообще их можно найти, только если уже знать, где вы находитесь.
Но моё открытие системы аксиом ответило на вопрос «Как далеко находится логика?» Для таких вещей, как клеточный автомат, довольно просто пронумеровать (как сделал я в 1980-х) все возможные клеточные автоматы. Чуть сложнее сделать это с системами аксиом –, но не сильно. В одном из подходов мою аксиому можно обозначить, как 411;3;7;118 — или, на языке Wolfram Language:
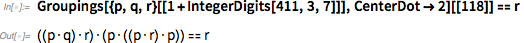
И, по крайней мере, в пространстве возможных функциональных форм (не учитывая разметку переменных) существует визуальное представление местонахождения этой аксиомы:

Учитывая фундаментальное значение логики для такого большого количества формальных систем, которые изучают люди, можно было подумать, что в любом разумном представлении логика соответствует одной из наипростейших из возможных систем аксиом. Но, по крайней мере в презентации, использующей NAND, это не так. Для неё всё ещё существует очень простая система аксиом, но это, вероятно, окажется стотысячная система аксиом из всех возможных, которые встретятся, если просто начать нумеровать системы аксиом, начиная с самой простой.
Учитывая это, очевидным следующим вопросом будет: что насчёт всех остальных систем аксиом? Как они ведут себя? Именно этот вопрос и исследует книга A New Kind of Science. И в ней я утверждаю, что такие вещи, как системы, наблюдаемые в природе, чаще всего лучше описываются этими самыми «другими правилами», которые мы можем найти, нумеруя возможности.
Что до систем аксиом, то я сделал картину, представляющую происходящее в «областях математики», соответствующих различным системам аксиом. Ряд показывает последствия определённой системы аксиом, а квадратики обозначают истинность определённой теоремы в данной системе аксиом (да, в какой-то момент вступает в силу теорема Гёделя, после чего становится невероятно сложно доказывать или опровергать заданную теорему в заданной системе аксиом; на практике, с моими методами это происходит чуть правее того, что изображено на картинке).

Есть ли что-то фундаментально особенное в областях математики, «исследованных людьми»? Судя по этой и другим картинкам, ничего очевидного в голову не приходит. Я подозреваю, что особенность у этих областей лишь одна — исторический факт того, что изучали именно их. (Можно делать заявления типа того, что «они описывают реальный мир» или «связаны с тем, как работает мозг», но результаты, описанные в книге, утверждают обратное).
Ну хорошо, а каково значение моей системы аксиом для логики? Её размер даёт почувствовать итоговое информационное наполнение логики как аксиоматической системы. И заставляет считать — по крайней мере, пока — что нам нужно считать логику больше «конструкцией, изобретённой человеком», чем «открытием», случившимся по «естественным причинам».
Если бы история шла по-другому, и мы бы постоянно искали (как это делается в книге) множество возможных простейших систем аксиом, то мы, возможно, «открыли» бы систему аксиом для логики, как ту систему, чьи свойства нам кажутся интересными. Но поскольку мы изучили такое небольшое количество из всех возможных систем аксиом, думаю, разумно будет считать логику «изобретением» — специально созданной конструкцией.
В каком-то смысле в Средние века логика так и выглядела — когда возможные силлогизмы (допустимые виды аргументов) представлялись в виде латинской мнемоники вроде bArbArA и cElErAnt. Поэтому сейчас интересно находить мнемоническое представление того, что мы знаем сейчас, как простейшую систему аксиом для логики.
Начиная с ((p · q) · r) · (p · ((p · r) · p)) = r, можно представить каждую p · q в виде префикса или польской записи (обратной к «обратной польской записи» калькулятора HP) в виде Dpq — поэтому всю аксиому можно записать, как =DDDpqrDpDDprpr. Есть ещё английская мнемоника на эту тему — FIGure OuT Queue, где роли p, q, r играют u, r, e. Или можно смотреть на первые буквы слов в следующем предложении (где B — оператор, а в роли p, q, r выступают a, p, c): «Bit by bit, a program computed Boolean algebra«s best binary axiom covering all cases» [понемногу вычисленная при помощи программы лучшая бинарная аксиома булевой алгебры описывает все случаи].
Механика доказательства
Ладно, так как же доказать корректность моей системы аксиом? Первое, что приходит в голову — показать, что из неё можно вывести известную систему аксиом для логики — например, систему аксиом Шеффера:
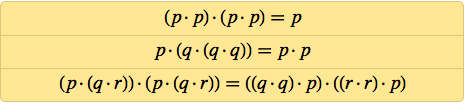
Здесь присутствуют три аксиомы, и нам надо вывести каждую. Вот, что можно сделать для вывода первой, при помощи последней версии Wolfram Language:
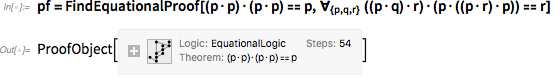
Примечательно, что сейчас стало возможным сделать это. В «объекте доказательства» записано, что для доказательства было использовано 54 шага. Исходя из этого объекта мы можем сгенерить «notebook », описывающий каждый из шагов:
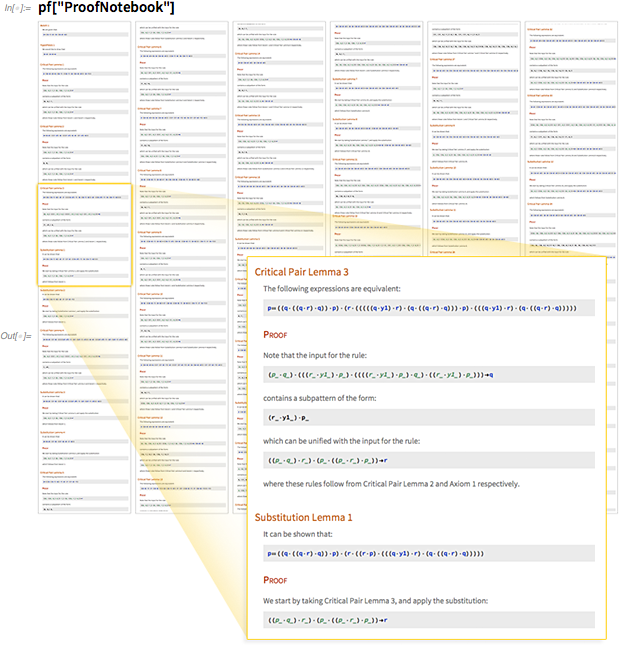
В общем здесь доказывается вся последовательность промежуточных лемм, что позволяет в итоге вывести конечный результат. Между леммами существует целая сеть взаимных зависимостей:
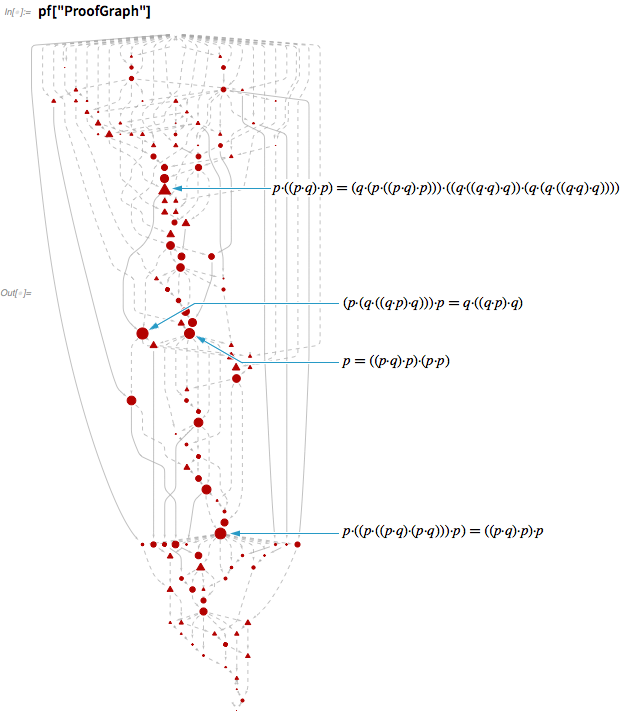
А вот сети, участвующие в выводе всех трёх аксиом в системе аксиом Шеффера — для последней используются невероятные 504 шага:

Да, очевидно, что эти сети довольно запутаны. Но перед тем, как обсудить, что означает эта сложность, поговорим о том, что происходит на каждом шаге этих доказательств.
Главная идея проста. Представим, что у нас есть аксиома, которая просто записывается, как p · q = q · p (математически это означает, что оператор коммутативен). Точнее, аксиома говорит, что для любых выражений p и q, p · q эквивалентно q · p.
Хорошо, допустим мы хотим вывести из этой аксиомы, что (a · b) · (c · d) = (d · c) · (b · a). Это можно сделать, используя аксиому для превращения d · c в c · d, b · a в a · b, и, наконец, (c · d) · (a · b) в (a · b) · (c · d).
FindEquationalProof делает по сути то же самое, хотя она выполняет эти шаги не совсем в том же порядке, и изменяет как левую часть уравнения, так и правую.
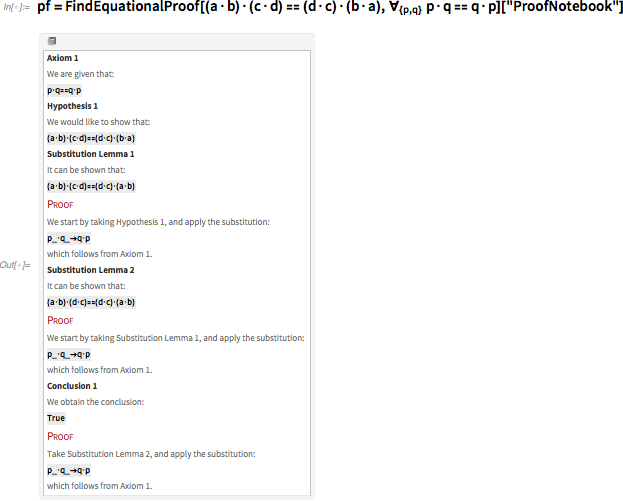
Получив такое доказательство, можно просто отследить каждый шаг и проверить, что они выдают заявленный результат. Но как найти доказательство? Существует множество возможных последовательностей подстановок и преобразований. Как найти последовательность, успешно доводящую до конечного результата?
Можно было бы решить: почему бы не попробовать все возможные последовательности, и если среди них есть рабочая, то она должна в итоге найтись? Проблема в том, что можно быстро прийти к астрономическому количеству последовательностей. Основная часть искусства автоматического доказательства теорем состоит из поиска способов уменьшения количества последовательностей для проверки.
Это быстро скатывается в технические подробности, но основную идею легко обсудить, если знать азы алгебры. Допустим, мы пытаемся доказать алгебраический результат вроде
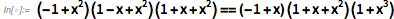
Существует гарантированный способ сделать это: просто применив правила алгебры для раскрытия каждой из сторон, можно сразу увидеть их сходство:
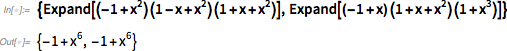
Почему это работает? Потому, что существует способ работы с такими выражениями, систематически уменьшающий их до тех пор, пока они не примут стандартную форму. А можно ли проделать такую же операцию в произвольных системах аксиом?
Не прямо сразу. В алгебре это работает, поскольку у неё есть особое свойство, гарантирующее, что всегда можно «продвигаться» по пути упрощения выражений. Но в 1970-х разные учёные несколько раз независимо друг от друга открыли (под названиями вроде алгоритм Кнута-Бендикса или базис Грёбнера), что даже если у системы аксиом нет необходимого внутреннего свойства, потенциально можно обнаружить «дополнения» этой системы, у которых оно есть.
Именно это происходит в типичных доказательствах, которые выдаёт FindEquationalProof (основанная на системе Валдмейстера, «master of trees»). Существуют т.н. «леммы критических пар», которые напрямую не продвигают доказательство, но делают возможным появление путей, способных на это. Усложняется всё из-за того, что, хотя окончательное выражение, которые мы хотим получить, довольно короткое, на пути к нему, возможно, приходится проходить через куда как более длинные промежуточные выражения. Поэтому, к примеру, у доказательства первой аксиомы Шеффера есть такие промежуточные шаги:
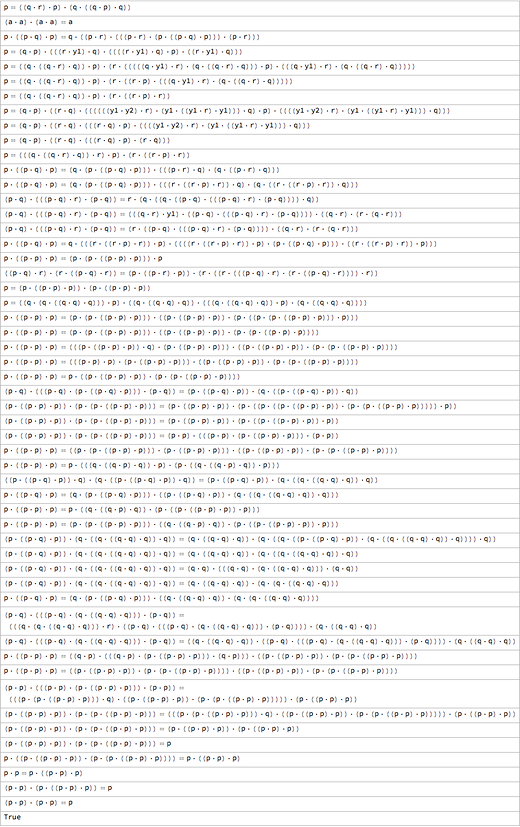
В данном случае крупнейший из шагов оказывается в 4 раза больше оригинальной аксиомы:
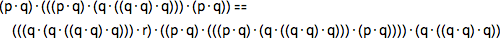
Такие выражения можно представлять в виде дерева. Вот его дерево, в сравнении с деревом первоначальной аксиомы:
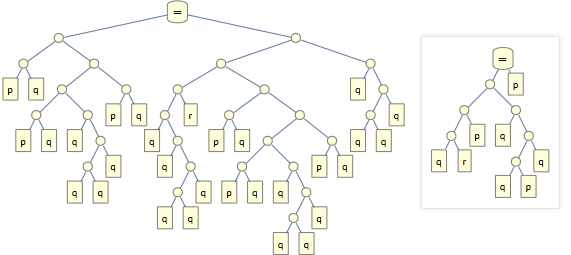
И вот как размеры промежуточных шагов развиваются в ходе доказательств каждой из аксиомы Шеффера:

Почему это так сложно?
Так ли удивительно, что эти доказательства настолько сложны? На самом деле, не особенно. Ведь нам хорошо известно, что математика бывает сложной. В принципе, могло быть и так, что все истины в математике было бы легко доказать. Но один из побочных эффектов теоремы Гёделя 1931 года состоит в том, что даже у тех вещей, у которых есть доказательства, путь к ним может быть сколь угодно длинным.
Это симптом гораздо более общего явления, которое я называю вычислительной несводимостью. Рассмотрим систему, управляемую простым правилом клеточного автомата (конечно, в любом моём эссе где-то обязательно будут клеточные автоматы). Запустим эту систему.
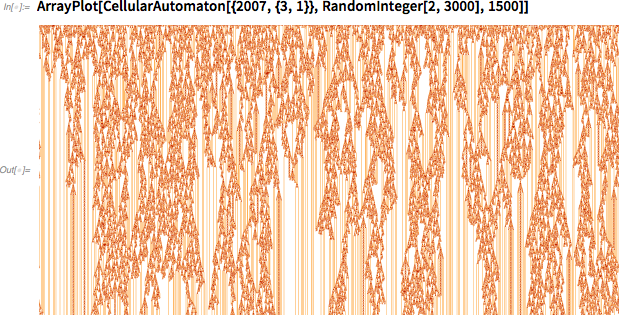
Можно было бы решить, что если в основе системы лежит простое правило, то должен быть быстрый способ понять, что делает система. Но это не так. Согласно моему принципу вычислительной эквивалентности, работа системы часто соответствует вычислениям, сложность которых совпадает с любыми вычислениями, которые мы могли бы провести, чтобы понять поведение системы. Это значит, что реальное поведение системы, по сути, соответствует такому количеству вычислительной работы, которое в принципе нельзя уменьшить.
Касательно картинки выше: допустим, мы хотим узнать, умрёт ли в итоге закономерность. Мы могли бы продолжать её выполнять, и если нам повезёт, она в итоге выродится во что-то, судьба чего будет очевидной. Однако в общем не существует верхней границы на то, сколько времени нам придётся потратить, по сути, на доказательство.
Когда что-то такое происходит с логическими доказательствами, оно происходит немного по-другому. Вместо того, чтобы запустить нечто, работающее по определённым правилам, мы спрашиваем, существует ли способ прийти к определённому результату, пройдя через несколько шагов, каждый из которых подчиняется определённому правилу. И эта задача, как практическая вычислительная задача, оказывается гораздо сложнее. Но суть сложности — это то же явление вычислительной несводимости, и это явление говорит о том, что не существует общего способа кратко обойти процесс изучения того, что сделает система.
Излишне говорить, что в мире существует множество вещей — особенно в технологии и научном моделировании, а также в областях, где присутствуют различные формы правил — традиционно разработанных так, чтобы избежать вычислительной несводимости, и работать так, чтобы результат их работы был сразу же виден, без необходимости проводить неуменьшаемое количество вычислений.
Но одно из следствий моего принципа вычислительной эквивалентности состоит в том, что эти случаи единичны и неестественные — он утверждает, что вычислительная несводимость существует во всех системах вычислительной вселенной.
А что же насчёт математики? Может, правила математики специально выбраны так, чтобы продемонстрировать вычислительную сводимость. И в некоторых случаях это так и есть (и в каком-то смысле это бывает и в логике). Но по большей части кажется, что системы аксиом математики не являются нетипичными для пространства всех возможных систем аксиом — где неизбежно буйствует вычислительная несводимость.
Зачем нужны доказательства?
В каком-то смысле, доказательство нужно, чтобы знать истинность чего-либо. Конечно, особенно в наше время, доказательство отошло на второй план, уступив место чистым вычислениям. На практике гораздо чаще встречается желание сгенерировать что-либо вычислениями, чем желание «отойти назад» и сконструировать доказательство истинности чего-либо.
В чистой математике, тем не менее, часто приходится сталкиваться с понятиями, включающими в себя, хотя бы номинально, бесконечное количество случаев («истинно для всех простых чисел», и т.п.), для которых вычисления «в лоб» не подойдут. А когда встаёт вопрос о подтверждении («может ли эта программа завершиться с ошибкой?» или «можно ли потратить эту криптовалюту дважды?») чаще разумнее попытаться до казать это, чем просчитать все возможные случаи.
Но в реальной математической практике, доказательство — это нечто большее, чем установление истины. Когда Евклид писал свои «Начала», он просто указывал результаты, а доказательства «оставлял читателю». Но, так или иначе, особенно за последнее столетие, доказательство превратилось в нечто, что не просто происходит за кулисами, а является основным носителем, через которые необходимо транслировать понятия.
Мне кажется, что в результате какой-то причуды истории доказательства сегодня предлагаются как предмет, который должны понять люди, а программы считаются просто чем-то, что должен исполнять компьютер. Почему так случилось? Ну, по крайней мере, в прошлом, доказательства можно было представлять в текстовом виде — поэтому, если их кто и использовал, то только люди. А программы практически всегда записывались в виде компьютерного языка. И очень долго эти языки создавались такими, чтобы их можно было более-менее напрямую транслировать в низкоуровневые операции компьютера — то есть, компьютер их понимал сразу, а люди — не обязательно.
Но одной из основных целей моей деятельности за последние несколько десятилетий было изменить такое положение вещей, и разработать в Wolfram Language настоящий «язык вычислительного общения», в котором вычислительные идеи можно передавать так, что их смогут понять и компьютеры, и люди.
У такого языка есть много последствий. Одно из них — изменение роли доказательства. Допустим, мы смотрим на какой-то математический результат. В прошлом единственным правдоподобным способом довести его до понимания было выдать доказательство, читаемое людьми. Но теперь возможно и другое: можно выдать программу для Wolfram Language, подсчитывающую результат. И это во многих смыслах гораздо более богатый способ донести истинность результата. Каждая часть программы представляет собой нечто точное и недвусмысленное — каждый желающий может её запустить. Нет такой проблемы, как попытки понять какую-то часть текста, требующие заполнять некие пробелы. Всё указано в тексте совершенно чётко.
Что насчёт доказательств? Есть ли недвусмысленные и точные способы писать доказательства? Потенциально да, хотя это не особенно легко. И хотя основа Wolfram Language существует уже 30 лет, только сегодня появился разумный способ представлять с его помощью такие структурно прямолинейные доказательства, как одна из моих аксиом выше.
Можно представить себе создание доказательств в Wolfram Language так же, как люди создают программы — и мы работаем над тем, чтобы предоставить высокоуровневые версии такой функциональности, «помогающей с доказательствами». Однако доказательство моей системы аксиом никто не создавал — его нашёл компьютер. И это уже больше похоже на выходные данные программы, чем на саму программу. Однако, как и программу, доказательство в некотором смысле тоже можно «запустить» для проверки результата.
Создавая понятность
Большую часть времени люди, использующие Wolfram Language, или Wolfram|Alpha, хотят что-то подсчитать. Им нужно получить результат, а не понять, почему они получили именно такие результаты. Но в Wolfram|Alpha, особенно в таких областях, как математика и химия, популярной среди студентов функцией является построение «пошаговых» решений.
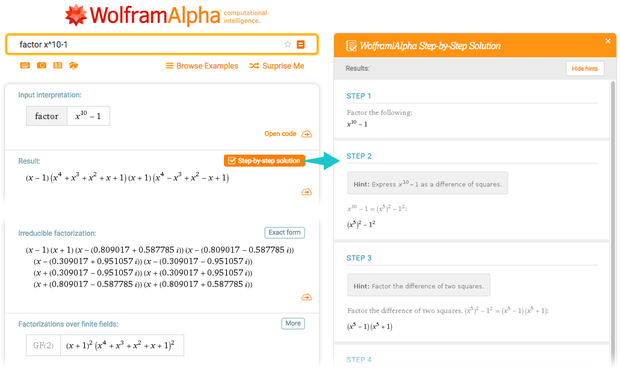
Когда систему Wolfram|Alpha вычисляет, например, интеграл, она использует всякие мощные алгоритмические техники, оптимизированные для получения ответов. Но когда её просят показать этапы расчётов, она делает нечто другое: ей нужно объяснить по шагам, почему получен именно такой результат.
Пользы в том, чтобы объяснить, как результат был получен на самом деле, не было бы; это очень неподходящий для человека процесс. Ей нужно понять, какие операции, выученные людьми, можно использовать для получения результата. Часто она придумывает какой-нибудь полезный трюк. Да, у неё есть систематический способ для этого, который всегда работает. Но в нём слишком много «механических» этапов. А «трюк» (подстановка, частичное интегрирование, и т.п.) не сработает в общем случае, но в данном конкретном он выдаст более быстрый путь к ответу.
А что же насчёт получения понятных версий других вещей? Например, работы программ в общем случае. Или доказательства моей системы аксиом.
Начнём с программ. Допустим, мы написали программу и хотим объяснить, как она работает. Один из традиционных подходов — включить в код комментарии. Если мы пишем на традиционном языке низкого уровня, это может быть лучшим выходом. Но вся суть Wolfram Language как языка вычислительного общения состоит в том, что сам язык должен позволять транслировать идеи, без необходимости включения дополнительных кусков текста.
Нужно затрачивать усилия на то, чтобы программа на Wolfram Language была хорошим описанием процесса, как и на то, чтобы простой текст на английском языке был хорошим описанием процесса. Однако можно получить такой кусок кода на Wolfram Language, который очень чётко объясняет, как всё работает, сам по себе.
Конечно, часто бывает так, что реальное выполнение кода приводит к таким вещам, которые не следуют очевидно из программы. Я вскоре упомяну о таких экстремальных случаях, как клеточные автоматы. Но пока что давайте представим, что мы создали программу, по которой можно представить, что она в целом делает.
В таком случае я обнаружил, что вычислительные эссе, представленные в виде Wolfram Notebooks, являются прекрасным инструментом для пояснения происходящего. Важно, что Wolfram Language, это позволяет запускать даже самые мелкие части программ по отдельности (с соответствующими символическими выражениями в роли входных и выходных данных). После этого можно представить себе последовательность шагов программы как последовательность элементов диалога, формирующего основу вычислительной записной книжки.
На практике часто необходимо создавать визуализации входных и выходных данных. Да, всё можно выразить в виде однозначного символического представления. Но людям гораздо проще понимать визуальное представление вещей, чем какую-нибудь одномерную языкоподобную строчку.
Конечно, создание хороших визуализаций сродни искусству. Но в Wolfram Language мы проделали большую работу по автоматизации этого искусства — часто при помощи довольно сложного машинного обучения и других алгоритмов, выполняющих такие вещи, как раскладка сетей или графических элементов.
Что насчёт того, чтобы начать с простого отслеживания работы программы? Это тяжело сделать. Я десятилетиями экспериментировал с этим, и никогда не был полностью удовлетворён результатами. Да, можно увеличить масштаб и увидеть множество деталей происходящего. Но я так и не обнаружил достаточно хороших техник, позволяющих понять всю картину целиком, и автоматически выдающих какие-то особенно полезные вещи.
На каком-то уровне эта задача похожа на реверс-инжиниринг. Вам демонстрируют машинный код, схему чипа, что угодно. А вам надо сделать шаг назад и воссоздать высокоуровневое описание, от которого отталкивался человек, которое каким-то образом «скомпилировалось» в то, что вы видите.
В традиционном подходе к инженерному делу, когда люди создают продукт по шагам, всегда имея возможность предвидеть последствия того, что они создают, этот подход в принципе может сработать. Но если вместо этого просто бродить по вычислительной вселенной в поисках оптимальной программы (так, как я искал воз
