[Перевод] Лабиринты: классификация, генерирование, поиск решений29.03.2019 13:05

Идеальный: для создания стандартного идеального лабиринта обычно необходимо «выращивать» его, обеспечив отсутствие петель и изолированных областей. Начинаем с внешней стены и случайным образом добавляем касающийся её фрагмент стены. Продолжаем случайным образом добавлять в лабиринт сегменты стен, но проверяем, что каждый новый сегмент касается с одного конца существующей стены, а его другой конец находится в ещё несозданной части лабиринта. Если вы добавляете сегмент стены, оба конца которого отделены от остального лабиринта, то это создаст несоединённую стену с петлёй вокруг, а если добавить сегмент, оба конца которого касаются лабиринта, то это создать недостижимую область. Это метод добавления стен; почти аналогично ему вырезание проходов, при котором части проходов вырезаются таким образом, чтобы существующего прохода касался только один конец.

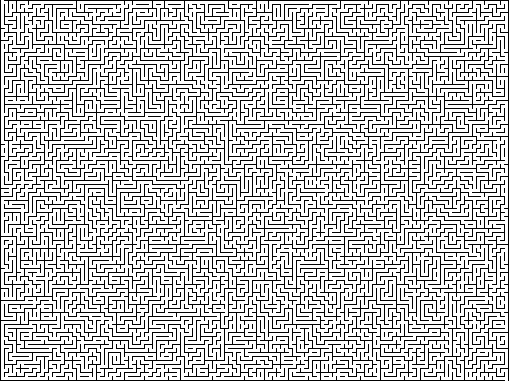
Плетёный: для создания лабиринта без тупиков по сути нужно добавлять в лабиринт сегменты стен случайным образом, но делать так, чтобы каждый новый добавляемый сегмент не приводил к созданию тупика. Я создаю их за четыре этапа: (1) начинаю с внешней стены, (2) обхожу лабиринт и добавляю отдельные сегменты стены, касающиеся каждой вершины стены, чтобы в лабиринте не было открытых комнат или небольших стен-«столбов», (3) обхожу все возможные сегменты стен в случайном порядке, добавляя стену там, где она не создаст тупика, (4) или запускаю процедуру удаления изолированных областей в конце, чтобы лабиринт был правильным и имел решение, или поступаю умнее на этапе (3) и делаю так, чтобы стена добавлялась только тогда, когда она не может привести к изолированной области.

Одномаршрутный: один из способов создания случайного одномаршрутного лабиринта — создать идеальный лабиринт, закрыть выход, чтобы остался только один вход, а затем добавлять стены, разделяющие каждый проход на две части. Это превращает каждый тупик в U-образный поворот, и у нас получится одномаршрутный проход, начинающийся и заканчивающийся в начале исходного лабиринта, который будет следовать по тому же пути, как и перемещение вдоль стены исходного лабиринта. Новый одномаршрутный лабиринт будет иметь удвоенный относительно исходного идеального лабиринта размер. Можно добавить небольшие хитрости, чтобы начало и конец не всегда находились друг рядом с другом: при создании идеального лабиринта мы никогда не будем добавлять сегменты, соединяющиеся с правой или нижней стенами, поэтому получившийся лабиринт будет иметь простое решение, следующее вдоль стены. Поставим вход в правом верхнем углу, и после разбиения пополам для создания одного маршрута удалим правую и нижнюю стены. В результате получится одномаршрутный лабиринт, начинающийся в правом верхнем углу и заканчивающийся в левом нижнем.

Разреженный:

разреженные лабиринты создаются решением не выращивать лабиринт в областях, которые будут нарушать правило разреженности. Для целостной реализации этого нужно при выборе новой вырезаемой ячейки сначала проверять все ячейки, находящиеся в полукруге выбранного радиуса ячеек, расположенных впереди от текущего направления. Если какая-то из этих ячеек уже является частью лабиринта, то мы не позволяем рассматривать эти ячейки, потому что в противном случае они будут слишком близко к существующей ячейке, а значит, превратят лабиринт в неразреженный. 3D: трёхмерные лабиринты и лабиринты большей размерности можно создавать точно так же, как стандартный двухмерный идеальный лабиринт, только из каждой ячейки можно случайным образом двигаться в шесть, а не в четыре ортогональные ячейки. Из-за дополнительных размерностей в этих лабиринтах обычно используется вырезание проходов.

Переплетённый: переплетённые лабиринты по сути создаются как идеальные лабиринты с вырезанием проходов, только при вырезании проходов мы не всегда ограничены существующим проходом, потому что у нас есть возможность пройти под ним и всё равно сохранить идеальность лабиринта. В монохромном растровом изображении переплетённый лабиринт можно представить четырьмя строками на проход (двух строк на проход достаточно для стандартного идеального лабиринта): одна строка для самого прохода, а остальные три строки недвусмысленно показывают, когда другой соседний проход идёт под ним, а не просто образует тупик рядом с первым проходом. Ради эстетичности перед вырезанием под уже готовым проходом можно заглядывать вперёд, чтобы убедиться. что можно продолжить вырезание, находясь под ним; так можно избежать тупиков, расположенных прямо под другими проходами. Также после вырезания под проходом можно инвертировать соседние с пересечением пиксели, чтобы новые проходы проходили над старыми, а не под ними.

Crack: Crack-лабиринты по сути создаются как идеальные лабиринты с добавлением стен, только в них нет отчётливой тесселяции, за исключением случайного расположения пикселей. Выбираем пиксель, который уже поставлен как стена, выбираем ещё одну случайную локацию, и «стреляем» или начинаем рисовать стену в сторону второй локации. Однако нужно останавливаться, не доходя до уже существующих стен, чтобы не создать изолированности. Завершаем работу, если какое-то время не можем добавить новых значимых стен. Учтите, что случайные локации для рисования могут находится в любом месте лабиринта, поэтому по лабиринту будет проходить несколько прямых линий и множество пропорционально меньших стен; количество стен ограничено только пиксельным разрешением. Это делает лабиринт очень похожим на поверхность листа, то есть по сути это фрактальный лабиринт.

Омега: для лабиринтов в стиле «омега» необходимо задать некую сетку, способ соединения ячеек друг с другом и привязку к экрану вершин, окружающих каждую ячейку. Например, для треугольного дельта-лабиринта с соединяющимися треугольными ячейками: (1) есть сетка, в которой количество ячеек в каждой следующей строке увеличивается на две. (2) Каждая ячейка соединяется с ячейками, соседними с ней в этом ряду, за исключением третьего прохода, который соединён с соответствующей ячейкой строкой выше или ниже, в зависимости от того, нечётный или чётный этот столбец (т.е. смотрил ли треугольник вверх или вниз). (3) Каждая ячейка использует математику треугольников, чтобы определить, где отрисовывать его на экране. Можно заранее отрисовать все стены на экране и вырезать в лабиринте проходы, или хранить в памяти некий изменяемый массив и рендерить всё после завершения.

Гиперлабиринт: гиперлабиринт — это 3D-среда, похожая на обратную версию стандартного трёхмерного не-гиперлабиринта, в котором блоки становятся открытыми пространствами, и наоборот. Хотя стандартный 3D-лабиринт состоит из дерева проходов через сплошную площадь, гиперлабиринт состоит из дерева полос или лиан, проходящих по открытой площади. Для создания гиперлабиринта мы начинаем со сплошных верхней и нижней граней, а затем выращиваем извилистые лианы из этих граней для заполнения пространства между ними, чтобы усложнить прохождение отрезка прямой между этими двумя гранями. Если каждая лиана соединяется с верхней или нижней частью, то гиперлабиринт будет иметь хотя бы одно простое решение. Если ни одна лиана не соединяется и с верхней, и с нижней частями (что создаст непроходимый столбец), то пока в верхней и нижней частях нет петель лиан, которые заставляют их неразрывно соединяться друг с другом подобно цепи, гиперлабиринт будет оставаться решаемым.

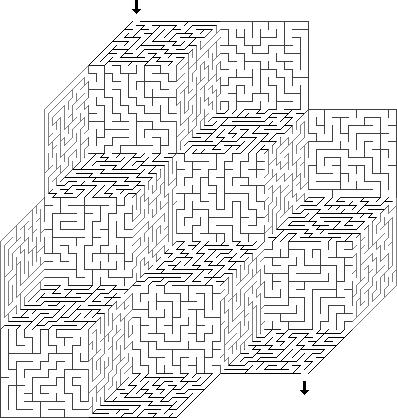
Planair: Planair-лабиринты с необычной топологией обычно создаются как массив из одного или нескольких лабиринтов или частей лабиринтов, в которых определён способ соединения краёв друг с другом. Лабиринт на поверхности куба — это всего лишь шесть квадратных частей лабиринта. Когда создаваемая часть доходит до края, то она перетекает в следующую часть и в правый край.

Шаблон:

лабиринты, основанные на шаблонах, создаются, начиная с базового изображения-шаблона, а затем запускается устранитель изолированных областей, обеспечивающий наличие решения лабиринта, за которым следует устранитель петель, повышающий сложность лабиринта. В результате создаётся идеальный лабиринт, очень похожий на исходное изображение. Например, для создания лабиринта, состоящего из пересекающихся спиралей нужно просто создать случайные спирали, не волнуясь о том, являются ли они лабиринтом, а затем пропустить их через устранители изолированных областей и петель.

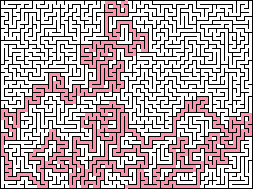
Recursive backtracker: он в чём-то похож на метод решения лабиринтов recursive backtracker, и требует стека, объём которого может доходить до размеров лабиринта. При вырезании он ведёт себя максимально жадно, и всегда вырезает проход в несозданной части, если она существует рядом с текущей ячейкой. Каждый раз, когда мы перемещаемся к новой ячейке, записываем предыдущую ячейку в стек. Если рядом с текущей позицией нет несозданных ячеек, то извлекаем из стека предыдущую позицию. Лабиринт завершён, когда в стеке больше ничего не остаётся. Это приводит к созданию лабиринтов с максимальным показателем текучести, тупиков меньше, но они длиннее, а решение обычно оказывается очень долгим и извилистым. При правильной реализации он выполняется быстро, и быстрее работают только очень специализированные алгоритмы. Recursive backtracking не может работать с добавлением стен, потому что обычно приводит к пути решения, следующему по внешнему краю, когда вся внутренняя часть лабиринта соединена с границей одним проходом.

Алгоритм Краскала: это алгоритм, создающий минимальное связующее дерево. Это интересно, потому что он не «выращивает» лабиринт подобно дереву, а скорее вырезает сегменты проходов по всему лабиринту случайным образом, и тем не менее в результате создаёт в конце идеальный лабиринт. Для его работы требуется объём памяти, пропорциональный размеру лабиринта, а также возможность перечисления каждого ребра или стены между ячейками лабиринта в случайном порядке (обычно для этого создаётся список всех рёбер и перемешивается случайным образом). Помечаем каждую ячейку уникальным идентификатором, а затем обходим все рёбра в случайном порядке. Если ячейки с обеих сторон от каждого ребра имеют разные идентификаторы, то удаляем стену и задаём всем ячейкам с одной стороны тот же идентификатор, что и ячейкам с другой. Если ячейки на обеих сторонах стены уже имеют одинаковый идентификатор, то между ними уже существует какой-то путь, поэтому стену можно оставить, чтобы не создавать петель. Этот алгоритм создаёт лабиринты с низким показателем текучести, но не таким низким, как у алгоритма Прима. Объединение двух множество по обеим сторонам стены будет медленной операцией, если у каждой ячейки есть только номер и они объединяются в цикле. Объединение, а также поиск можно выполнять почти за постоянное время благодаря использованию алгоритма объединения-поиска (union-find algorithm): помещаем каждую ячейку в древовидную структуру, корневым элементом является идентификатор. Объединение выполняется быстро благодаря сращиванию двух деревьев. При правильной реализации этот алгоритм работает достаточно быстро, но медленнее большинства из-за создания списка рёбер и управления множествами.

Алгоритм Прима (истинный): этот алгоритм создаёт минимальное связующее дерево, обрабатывая уникально случайные веса рёбер. Объём требуемой памяти пропорционален размеру лабиринта. Начинаем с любой вершины (готовый лабиринт будет одинаковым, с какой бы вершины мы ни начали). Выполняем выбор ребра прохода с наименьшим весом, соединяющим лабиринт к точке, которая ещё в нём не находится, а затем присоединяем её к лабиринту. Создание лабиринта завершается, когда больше не осталось рассматриваемых рёбер. Для эффективного выбора следующего ребра необходима очередь с приоритетом (обычно реализуемая с помощью кучи), хранящая все рёбра границы. Тем не менее, этот алгоритм достаточно медленный, потому что для выбора элементов из обработка кучи требует времени log (n). Поэтому лучше предпочесть алгоритм Краскала, который тоже создаёт минимальное связующее дерево, ведь он быстрее и создаёт лабиринты с идентичной структурой. На самом деле при одинаковом случайном seed алгоритмами Прима и Краскала можно создавать одинаковые лабиринты.

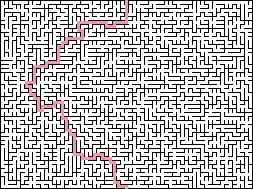
Алгоритм Прима (упрощённый): этот алгоритм Прима создаёт минимальное связующее дерево. Он упрощён таким образом, что все веса рёбер одинаковы. Для него требуется объём памяти, пропорциональный размеру лабиринта. Начинаем со случайной вершины. Выбираем случайным образом ребро прохода, соединяющее лабиринт с точкой, которая ещё не в нём, а затем присоединяем её к лабиринту. Лабиринт оказывается завершённым, когда больше не остаётся рассматриваемых рёбер. Так как рёбра не имеют веса и не упорядочены, их можно хранить как простой список, то есть выбор элементов из списка будет очень быстрым и занимает постоянное время. Поэтому он намного быстрее истинного алгоритма Прима со случайными весами рёбер. Создаваемая текстура лабиринта будет иметь меньший показатель текучести и более простое решение, чем у истинного алгоритма Прима, потому что распространяется из начальной точки равномерно, как пролитый сироп, а не обходит фрагменты рёбер с более высоким весом, которые учитываются позже.

Алгоритм Прима (модифицированный): этот алгоритм Прима создаёт минимальное связующее дерево, изменённое так, что все веса рёбер одинаковы. Однако он реализован таким образом, что вместо рёбер смотрит на ячейки. Объём памяти пропорционален размеру лабиринта. В процессе создания каждая ячейка может иметь один из трёх типов: (1) «внутренняя»: ячейка является частью лабиринта и уже вырезана в нём, (2) «граничная»: ячейка не является частью лабиринта и ещё не вырезана в нём, но находится рядом с ячейкой, которая уже является «внутренней», и (3) «внешняя»: ячейка ещё не является часть лабиринта, и ни один из её соседей тоже не является «внутренней» ячейкой. Начинаем с выбора ячейки, делаем её «внутренней», а для всех её соседей задаём тип «граничная». Выбираем случайным образом «граничную» ячейку и вырезаем в неё проход из одной из соседних «внутренних» ячеек. Меняем состояние этой «граничной» ячейки на «внутреннюю» и изменяем тип всех её соседей с «внешней» на «граничную». Лабиринт завершён, когда больше не остаётся «граничных» ячеек (то есть не осталось и «внешних» ячеек, а значит, все стали «внутренними»). Этот алгоритм создаёт лабиринты с очень низким показателем текучести, имеет множество коротких тупиков и довольно прямолинейное решение. Полученный лабиринт очень похож на результат упрощённого алгоритма Прима, за незначительным отличием: пустоты в связующем дереве заполняются, только если случайным образом выбирается граничная ячейка, в отличие от утроенной вероятности заполнения этой ячейки через одну из граничных ячеек, ведущих в неё. Кроме того, алгоритм очень быстр, быстрее упрощённого алгоритма Прима, потому что ему не нужно составлять и обрабатывать список рёбер.

Алгоритм Олдоса-Бродера: интересно в этом алгоритме то, что он однородный, то есть он с равной вероятностью создаёт все возможные лабиринты заданного размера. Кроме того, ему не требуется дополнительной памяти или стека. Выбираем точку и случайным образом перемещаемся в соседнюю ячейку. Если мы попали в невырезанную ячейку, то вырезаем в неё проход из предыдущей ячейки. Продолжаем двигаться в соседние ячейки, пока не вырежем проходы во все ячейки. Этот алгоритм создаёт лабиринты с низким показателем текучести, всего немного выше, чем у алгоритма Краскала. (Это значит, что для заданного размена существует больше лабиринтов с низким показателем текучести, чем с высоким, потому что лабиринт со средней равной вероятностью имеет низкий показатель.) Плохо в этом алгоритме то, что он очень медленный, так как не выполняет интеллектуального поиска последних ячеек, то есть по сути не имеет гарантий завершения. Однако из-за своей простоты он может быстро проходить по множеству ячеек, поэтому завершается быстрее, чем можно было бы подумать. В среднем его выполнение занимает в семь раз больше времени, чем у стандартных алгоритмов, хотя в плохих случаях оно может быть намного больше, если генератор случайных чисел постоянно избегает последних нескольких ячеек. Он может быть реализован как добавляющий стены, если стену границы считать единой вершиной, т.е., например, если ход перемещает нас к стене границы, мы телепортируемся к случайной точке вдоль границы, а уже потом продолжаем двигаться. В случае добавления стен он работает почти в два раза быстрее, потому что телепортация вдоль стены границы позволяет быстрее получать доступ к дальним частям лабиринта.

Алгоритм Уилсона: это усовершенствованная версия алгоритма Олдоса-Бродера, он создаёт лабиринты точно с такой же текстурой (алгоритмы однородны, то есть все возможные лабиринты генерируются с равной вероятностью), однако алгоритм Уилсона выполняется гораздо быстрее. Он занимает память вплоть до размеров лабиринта. Начинаем со случайно выбранной начальной ячейки лабиринта. Выбираем случайную ячейку, которая ещё не является частью лабиринта и выполняем случайный обход, пока не найдём ячейку, уже принадлежащую лабиринту. Как только мы наткнёмся на уже созданную часть лабиринта, возвращаемся к выбранной случайной ячейке и вырезаем весь проделанный путь, добавляя эти ячейки к лабиринту. Конкретнее, при возврате по пути мы в каждой ячейке выполняем вырезание в том направлении, в котором проходил случайный обход при последнем выходе из ячейки. Это позволяет избежать появления петель вдоль пути возврата, благодаря чему к лабиринту присоединяется один длинный проход. Лабиринт завершён, когда к нему присоединены все ячейки. Алгоритм имеет те же проблемы со скоростью, что и Олдос-Бродер, потому что может уйти много времени на нахождение первого случайного пути к начальной ячейке, однако после размещения нескольких путей остальная часть лабиринта вырезается довольно быстро. В среднем он выполняется в пять раз быстрее Олдоса-Бродера, и менее чем в два раза медленнее лучших алгоритмов. Стоит учесть, что в случае добавления стен он работает в два раза быстрее, потому что вся стена границы изначально является частью лабиринта, поэтому первые стены присоединяются гораздо быстрее.

Алгоритм Hunt and kill: этот алгоритм удобен, потому что не требует дополнительной памяти или стека, а потому подходит для создания огромных лабиринтов или лабиринтах на слабых компьютерах благодаря невозможности исчерпания памяти. Так как в нём нет правил, которым нужно следовать постоянно, его также проще всего модифицировать и создавать с его помощью лабиринты с разной текстурой. Он почти схож с recursive backtracker, только рядом с текущей позицией нет несозданной ячейки. Мы входим в режим «охоты» и систематично сканируем лабиринт, пока не найдём несозданную ячейку рядом с уже вырезанной ячейкой. На этом этапе мы снова начинаем вырезание в этой новой локации. Лабиринт завершён, когда в режиме «охоты» просканированы все ячейки. Этот алгоритм склонен к созданию лабиринтов с высоким показателем текучести, но не таким высоким, как у recursive backtracker. Можно заставить его генерировать лабиринты с более низким показателем текучести, чаще входя в режим «охоты». Он выполняется медленнее из-за времени, потраченного на охоту за последними ячейками, но не намного медленее, чем алгоритм Краскала. Его можно реализовать по принципу добавления стен, если время от времени случайным образом телепортироваться, чтобы избежать проблем, свойственных recursive backtracker.

Алгоритм выращивания
дерева (Growing tree algorithm): это обобщённый алгоритм, способный создавать лабиринты с разной текстурой. Требуемая память может достигать размера лабиринта. При каждом вырезании ячейки мы добавляем её в список. Выбираем ячейку из списка и вырезаем проход в несозданную ячейку рядом с ней. Если рядом с текущей нет несозданных ячеек, удаляем текущую ячейку из списка. Лабиринт завершён, когда в списке больше ничего нет. Интересно в алгоритме то, что в зависимости от способа выбора ячейки из списка можно создавать множество разных текстур. Например, если всегда выбирать последнюю добавленную ячейку, то этот алгоритм превращается в recursive backtracker. Если всегда выбирать ячейки случайно, то он ведёт себя похоже, но не идентично алгоритму Прима. Если всегда выбирать самые старые ячейки, добавленные в список, то мы создадим лабиринт с наименьшим возможным показателем текучести, даже ниже, чем у алгоритма Прима. Если обычно выбирать самую последнюю ячейку, но время от времени выбирать случайную ячейку, то лабиринт будет иметь высокий показатель текучести, но короткое и прямое решение. Если случайно выбирать одну из самых последних ячеек, то лабиринт будет иметь низкий показатель текучести, но долгое и извилистое решение.

Алгоритм выращивания леса (Growing forest algorithm): это более обобщённый алгоритм, сочетающий в себе типы, основанные на деревьях и множествах. Он является расширением алгоритма выращивания дерева, по сути включающего в себя несколько экземпляров, расширяющихся одновременно. Начинаем со всех ячеек, случайным образом отсортированных в список «новых»; кроме того, у каждой ячейки есть собственное множество, как в начале алгоритма Краскала. Сначлаа выбираем одну или несколько ячеек, перемещая их из списка «новых» в список «активных». Выбираем ячейку из «активного» списка и вырезаем проход в соседнюю несозданную ячейку из «нового» списка, добавляя новую ячейку в список «активных» и объединяя множества двух ячеек. Если предпринята попытка выполнить вырезание в существующую часть лабиринта, то разрешить её, если ячейки находятся в разных множествах, и объединить ячейки, как это делается в алгоритме Краскала. Если рядом с текущей ячейкой нет несозданных «новых» ячеек, то перемещаем текущую ячейку в список «готовых». Лабиринт завершён, когда становится пустым список «активных». В конце выполняем объединение всех оставшихся множеств, как в алгоритме Краскала. Периодически можно создавать новые деревья, перемещая одну или несколько ячеек из списка «новых» в список «активных», как это делалось в начале. Управляя количество изначальных деревьев и долей новых создаваемых деревьев, можно сгенерировать множество уникальных текстур, сочетающихся с и так уже гибкими параметрами алгоритма выращивания дерева.

Алгоритм Эллера: это особый алгоритм, потому что он не только быстрее всех остальных, но и не имеет очевидной смещённости или недостатков; кроме того, при его создании память используется наиболее эффективно. Для него даже не требуется, чтобы в памяти находился весь лабиринт, он использует объём, пропорциональный размеру строки. Он создаёт лабиринт построчно, после завершения генерации строки алгоритм больше её не учитывает. Каждая ячейка в строке содержится во множестве; две ячейки принадлежат одному множеству, если между ними есть путь по уже созданному лабиринту. Эта информация позволяет вырезать проходы в текущей строке без создания петель или изолированных областей. На самом деле это довольно похоже на алгоритм Краскала, только здесь формируется по одной строке за раз, в то время как Краскал просматривает весь лабиринт. Создание строки состоит из двух частей: случайным образом соединяем соседние в пределах строки ячейки, т.е. вырезаем горизонтальные проходы, затем случайным образом соединяем ячейки между текущей и следующей строками, т.е. вырезаем вертикальные проходы. При вырезании горизонтальных проходов мы не соединяем ячейки, уже находящиеся в одном множестве (потому что иначе создастся петля), а при вырезании вертикальных проходов мы должны соединить ячейку, если она имеет единичный размер (потому что если её оставить, она создаст изолированную область). При вырезании горизонтальных проходов мы соединяем ячейки, если они находятся в одинаковом множестве (потому что теперь между ними есть путь), а при вырезании вертикальных проходов когда не соединяемся с ячейкой, помещаем её в отдельное множество (потому что теперь она отделена от остальной части лабиринта). Создание начинается с того, что перед соединением ячеек в первой строке каждая ячейка имеет собственное множество. Создание завершается после соединения ячеек в последней строке. Существует особое правило завершения: к моменту завершения каждая ячейка должна находиться в одинаковом множестве, чтобы избежать изолированных областей. (Последняя строка создаётся объединением каждой из пар соседних ячеек, ещё не находящихся в одном множестве.) Лучше всего реализовывать множество с помощью циклического двусвязного списка ячеек (который может быть просто массивом, привязывающим ячейки к парам ячеек с обеих сторон того же множества), позволяющего выполнять за постоянное время вставку, удаление и проверку нахождения соседних ячеек в одном множестве. Проблема этого алгоритма заключается в несбалансированности обработки разных краёв лабиринта; чтобы избежать пятен в текстурах нужно выполнять соединение и пропуск соединения ячеек в правильных пропорциях.

Рекурсивное деление (Recursive division):

этот алгоритм чем-то похож на recursive backtracking, потому что в них обоих применяются стеки, только он работает не с проходами, а со стенами. Начинаем с создания случайной горизонтальной или вертикальной стены, пересекающей доступную область в случайной строке или столбце, и размещаем вдоль неё случайным образом пустые места. Затем рекурсивно повторяем процесс для двух подобластей, сгенерированных разделяющей стеной. Для наилучших результатов нужно добавить отклонение в выборе горизонтали или вертикали на основе пропорций области, например, область, ширина которой вдвое больше высоты, должна более часто делиться вертикальными стенами. Это самый быстрый алгоритм без отклонений в направлениях, и часто он может даже соперничать с лабиринтами на основе двоичных деревьев, потому что он создаёт одновременно несколько ячеек, хоть и имеет очевидный недостаток в виде длинных стен, пересекающих внутренности лабиринта. Этот алгоритм является разновидностью вложенных фрактальных лабиринтов, только вместо постоянного создания лабиринтов ячеек фиксированного размера с лабиринтами одного размера внутри каждой ячейки, он случайным образом делит заданную область на лабиринт случайного размера: 1×2 или 2×1. Рекурсивное деление нельзя использовать для вырезания проходов, потому что это приводит к созданию очевидного решения, которое или следует вдоль внешнего края, или иначе напрямую пересекает внутреннюю часть.

Лабиринты на основе двоичных деревьев: по сути, это самые простые и быстрые из возможных алгоритмов, однако создаваемые лабиринты имеют текстуру с очень высокой смещённостью. Для каждой ячейки мы вырезаем проход или вверх, или влево, но никогда не в обоих направлениях. В версии с добавлением стен для каждой вершины добавляется сегмент стены, ведущий вниз или вправо, но не в обоих направлениях. Каждая ячейка независима от всех других ячеек, потому что нам не нужно при её создании проверять состояние каких-то других ячеек. Следовательно, это настоящий алгоритм генерации лабиринтов без памяти, не ограниченный по размерам создаваемых лабиринтов. По сути, это двоичное дерево, если рассматривать верхний левый угол как корень, а каждый узел или ячейка имеет один уникальный родительский узел, являющийся ячейкой сверху или слева от неё. Лабиринты на основе двоичных деревьев отличаются от стандартных идеальных лабиринтов, потому что в них не может существовать больше половины типов ячеек. Например, в них никогда не будет перекрёстков, а все тупики имеют проходы, ведущие вверх или влево, и никогда не ведущие вниз или вправо. Лабиринты склонны иметь проходы, ведущие по диагонали из верхнего левого в нижний правый угол, и по ним гораздо проще двигаться из нижнего правого в верхний левый угол. Всегда можно перемещаться вверх или влево, но никогда одновременно в оба направления, поэтому всегда можно детерминированно перемещаться по диагонали вверх и влево, не сталкиваясь с барьерами. Иметь возможность выбора и попадать в тупики вы начнёте, перемещаясь вниз и вправо. Учтите, что если перевернуть лабиринт двоичного дерева вниз головой и считать проходы стенами, и наоборот, то результатом по сути будет другое двоичное дерево.

Лабиринты Sidewinder:

этот простой алгоритм очень похож на алгоритм двоичного дерева, но немного более сложен. Лабиринт генерируется по одной строке за раз: для каждой ячейки случайным образом выбирается, нужно ли вырезать проход, ведущий вправо. Если проход не вырезан, то мы считаем, что только что завершили горизонтальный проход, образованный текущей ячейкой и всеми ячейками слева, вырезавшими проходы, ведущими в неё. Случайным образом выбираем одну ячейку вдоль этого прохода и вырезаем проход, ведущий из неё вверх (это должна быть текущая ячейка, если соседняя ячейка не вырезала проход). В 

© Habrahabr.ru