[Перевод] Книга Алана Тьюринга и загадочная записка — Научный детектив

Оригинал перевода в моём блоге
Как ко мне попала эта книга?
В мае 2017 года я получил электронное письмо от моего старого учителя средней школы по имени Джордж Раттер, в котором он писал:»У меня есть копия большой книги Дирака на немецком языке (Die Prinzipien der Quantenmechanik), которая принадлежала Алану Тьюрингу, и после того как я прочел вашу книгу Создатели идей (Idea Makers), мне показалось само собой разумеющимся, что вы именно тот человек, которому она нужна». Он объяснил мне, что получил книгу от другого (к тому времени умершего) моего школьного учителя Нормана Рутледжа, о котором я знал, что он был другом Алана Тьюринга. Джордж закончил свое письмо фразой:»Если вам нужна эта книга, я мог бы вручить ее вам в следующий раз, когда вы приедете в Англию».
Спустя пару лет в марте 2019 года я действительно прибыл в Англию, после чего договорился с Джорджем о встрече за завтраком в небольшом отеле в Оксфорде. Мы ели, болтали и ждали, пока еда уляжется. Затем настал подходящий момент для обсуждения книги. Джордж сунул руку в портфель и вытащил довольно скромно оформленный, типичный академический томик середины 1900-х годов.

Я открыл обложку, размышляя, не может ли на ней быть с обратной стороны надписи:»Собственность Алана Тьюринга» или чего-то в этом духе. Но, к сожалению, это оказалось не так. Тем не менее к ней была приложена достаточно выразительная записка на четырех листах от Нормана Рутледжа к Джорджу Раттеру, написанная в 2002 году.
Я знал Нормана Рутледжа, когда еще был учеником средней школы в Итоне в начале 1970-х годов. Он был учителем математики по прозвищу «Чокнутый Норман». Он был приятным во всех отношениях преподавателем и рассказывал бесконечные байки о математике и о всяких других занимательных вещах. Он был ответственным за то, чтобы школа получила компьютер (программируемый с помощью перфоленты шириной с парту) — это был самый первый компьютер, который я когда-либо использовал.
В те времена я ничего не знал о прошлом Нормана (помните, что это было задолго до появления Интернета). Я знал только о том, что он был «Доктором Рутледжем». Он достаточно часто рассказывал истории о людях из Кембриджа, но в своих рассказах он никогда не упоминал Алана Тьюринга. Конечно, Тьюринг тогда еще не был достаточно знаменит (хотя, как выясняется, я уже слышал о нем от кого-то, кто знал его в Блетчли-Парке (особняк в котором во время Второй мировой войны располагался шифровальный центр)).
Алан Тьюринг не был знаменит вплоть до 1981 года, когда я впервые начал изучать простые программы, хотя тогда еще в контексте клеточных автоматов, а не машин Тьюринга.
Как вдруг однажды, просматривая каталог карточек в библиотеке Калифорнийского технологического института, я наткнулся на книгу «Алан М. Тьюринг», написанную его мамой Сарой Тьюринг. В книге было много информации, в том числе о неопубликованных научных трудах Тьюринга по биологии. Однако я ничего не узнал о его отношениях с Норманом Рутледжем, так как в книге ничего не упоминалось о нем (хотя, как я выяснил, Сара Тьюринг переписывалась с Норманом об этой книге, и Норман даже в итоге написал рецензию к ней).

Десять лет спустя, настроенный с крайним любопытством к Тьюрингу и его (тогда еще неопубликованным) работам по биологии, я посетил архив Тьюринга в Королевском колледже в Кембридже. Вскоре, ознакомившись с тем, что у них было из работ Тьюринга, и потратив на это некоторое время, я подумал, что заодно могу попросить посмотреть также и его личную переписку. Просматривая её, я обнаружил несколько писем от Алана Тьюринга к Норману Рутледжу.
К тому времени вышла в свет биография Эндрю Ходжеса, которая так много сделала для того, чтобы Тьюринг наконец стал знаменитым, в ней подтвердилось — Алан Тьюринг и Норман Рутледж действительно были друзьями, а также то, что Тьюринг был научным консультантом Нормана. Я хотел спросить Рутледжа о Тьюринге, но к тому времени Норман уже был на пенсии и вел уединенный образ жизни. Тем не менее, когда я завершил работу над книгой »Новый вид науки» в 2002 году (после моего десятилетнего затворничества), я разыскал его и послал ему копию книги с подписью «Моему последнему учителю математики». Затем мы с ним немного попереписывались, и в 2005 году я снова приехал в Англию и договорился встретиться с Норманом попить чайку в роскошном отеле в центре Лондона.
Мы мило побеседовали о многом, в том числе и об Алане Тьюринге. Норман начал нашу беседу с рассказа о том, что действительно знал Тьюринга, по большей части поверхностно, 50 лет тому назад. Но все же ему было что рассказать и о нем лично:»Он был нелюдим».»Он много хихикал».»Он не мог по-настоящему говорить с нематематиками».»Он всегда боялся расстроить свою мать».»Он уходил днем и пробегал марафон».»Он не был слишком амбициозным». Затем разговор вернулся к личности Нормана. Он сказал, что, несмотря на то, что он уже как 16 лет ушел на пенсию, он по-прежнему пишет статьи для «Математической газеты», чтобы, по его словам,»доделать все свои научные труды прежде чем перейти в мир иной», где, как он добавил с едва заметной улыбкой,»все математические истины обязательно будут раскрыты». Когда чаепитие закончилось, Норман надел свою кожаную куртку и направился к своему мопеду, совершенно не обращая внимания на взрывы, которые нарушили движение транспорта в Лондоне в тот день.
Это был последний раз, когда я видел Нормана, он умер в 2013 году.
Шесть лет спустя я сидел за завтраком с Джорджем Раттером. Со мной была записка от Рутледжа, написанная им в 2002 году его характерным почерком:

Сначала я бегло прочитал записку. Она как обычно была экспрессивной:
Я получил книгу Алана Тьюринга от его друга и душеприказчика Робина Гэнди (в Королевском колледже было в порядке вещей раздавать книги из собрания умерших товарищей, и я выбрал собрание стихов А.Э. Хаусмана из книг Айвора Рамсея в качестве подходящего подарка (он был деканом и спрыгнул с часовни [в 1956 году])…
Позже в короткой записке он пишет:
Вы спрашиваете, куда, в конце концов, должна была попасть эта книга — по моему мнению, она должна попасть тому, кто ценит все, что связано с работами Тьюринга, так что ее судьба зависит от вас.Стивен Вольфрам прислал мне свою впечатляющую книгу, но я недостаточно глубоко окунулся в нее…
В заключение он поздравил Джорджа Раттера с тем, что у него хватило смелости переехать (как оказалось, временно) в Австралию после ухода на пенсию, сказав, что он сам »поиграл бы в переезд в Шри-Ланку как пример дешевого и лотосоподобного существования», но добавил, что »события, происходящие сейчас там, указывают на то, что он не должен был этого делать» (по-видимому, имея в виду гражданскую войну в Шри-Ланке).
Так что же скрывается в недрах книги?
Итак, что же я сделал с копией книги на немецком языке, написанной Полем Дираком, которая когда-то принадлежала Алану Тьюрингу. Я не читаю по-немецки, но у меня была копия этой же книги на английском языке (который является языком ее оригинала) издания 1970-х годов. Тем не менее, однажды за завтраком мне показалось правильным, что я должен внимательно просмотреть книгу постранично. В конце концов, это общепринятая практика, когда имеют дело с антикварными книгами.
Следует отметить, что меня поразила элегантность изложения Дирака. Книга была опубликована в 1931 году, но ее чистый формализм (и, да, несмотря на языковой барьер, я мог читать математику, которая изложена в книге) почти такой же, как если бы ее написали сегодня. (Я не хочу здесь слишком акцентироваться на Дираке, но мой друг Ричард Фейнман сказал мне, что, по крайней мере, по его мнению изложение Дирака односложно. Норман Рутледж сказал мне, что он дружил в Кембридже с приемным сыном Дирака, который стал теоретиком в области графов. Норман довольно часто бывал в доме Дирака и рассказывал, что «великий человек» иногда лично отходил как бы на второй план, тогда как на первом всегда было множество математических головоломок. Я сам, к сожалению, никогда не встречал Поля Дирака, хотя мне сказали, что после того, как он, наконец, ушел из Кембриджа и отправился во Флориду, он утратил большую часть своей прежней жесткости и стал довольно общительным человеком).
Но вернемся к книге Дирака, которая принадлежала Тьюрингу. На странице 9 я заметил подчеркивания и небольшие пометки на полях, написанные простым карандашом. Я продолжал листать страницы. После нескольких глав пометки исчезли. Но затем, внезапно, я обнаружил вложенную в страницу 127 записку следующего содержания:
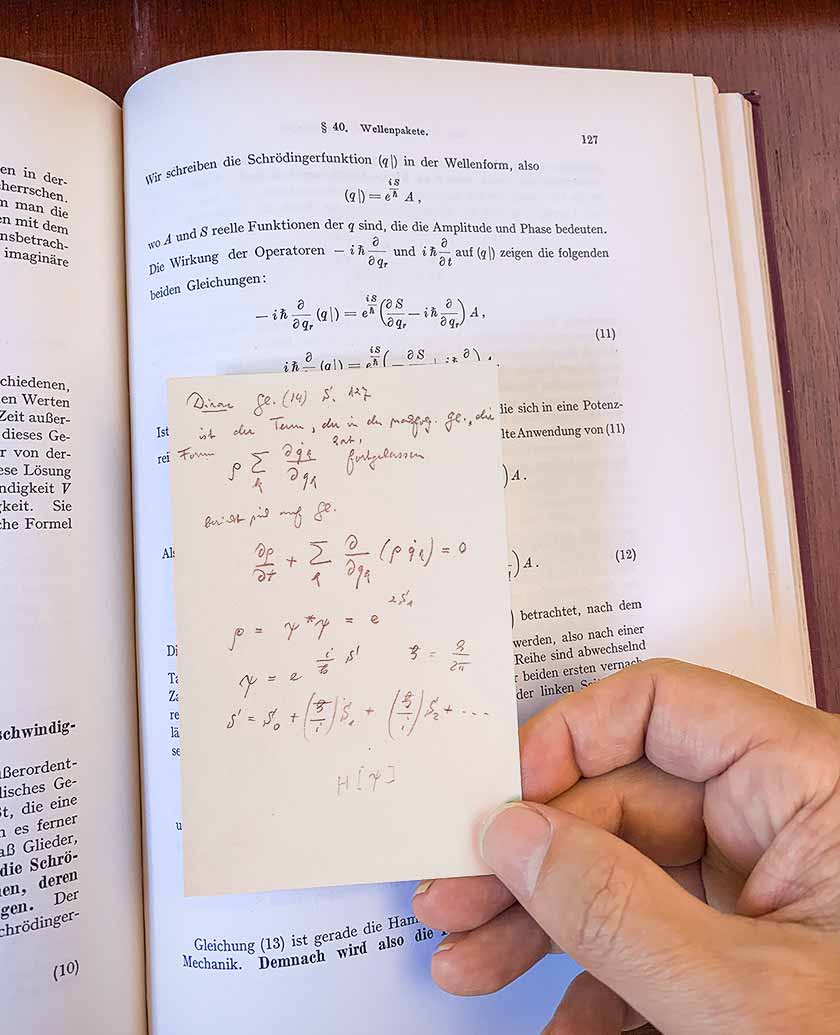
Она была написана на немецком языке стандартным немецким почерком. И похоже на то, что она как-то могла быть связана с лагранжевой механикой. Я подумал, что, вероятно, кто-то владел данной книгой до Тьюринга, и это, должно быть, записка, написанная этим человеком.
Я продолжал листать книгу. Заметки отсутствовали. И я подумал, что больше не смогу ничего найти. Но затем, на странице 231 я обнаружил, фирменную закладку — с отпечатанным текстом:

Обнаружу ли я в итоге что-нибудь еще? Я продолжал листать книгу. Затем, в конце книги, на странице 259, в разделе, посвященном релятивистской теории электронов, я обнаружил следующее:

Я развернул этот лист бумаги:
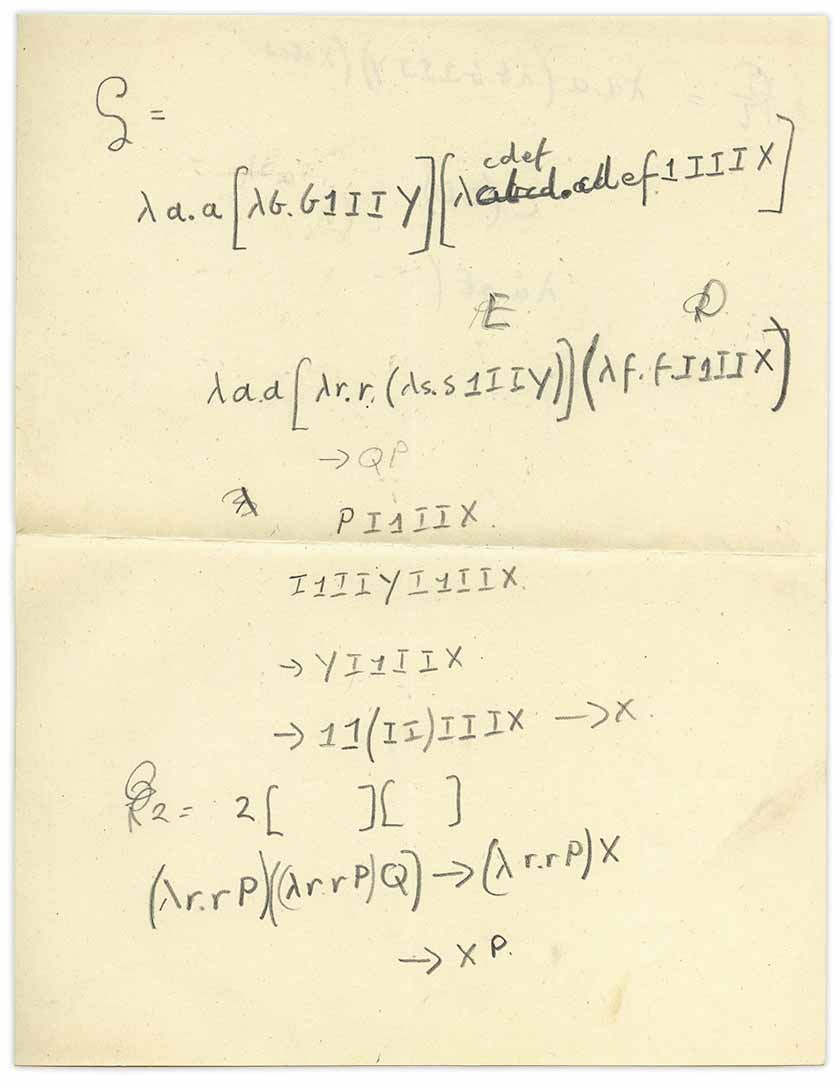
Я сразу понял, что это лямбда-исчисление с примесью комбинаторов, но как же этот лист тут оказался? Напомним, что данная книга является книгой о квантовой механике, но во вложенном листке речь идет о математической логике, или о том, что сейчас называется теорией вычислений. Это является типичным для трудов Тьюринга. Мне стало интересно, написал ли лично Тьюринг эту записку?
Даже во время завтрака я искал в Интернете образцы почерка Тьюринга, но не нашел примеров в виде расчетов, поэтому не смог сделать заключений о точной принадлежности почерка. И вскоре надо было идти. Я бережно упаковал книгу, готовую раскрыть тайну того, что это была за страница и кто ее написал, и взял ее с собой.
О книге
Прежде всего давайте обсудим саму книгу. «Принципы квантовой механики» Поля Дирака были опубликованы на английском языке в 1930 году и вскоре были переведены на немецкий язык. (Предисловие Дирака датировано 29 мая 1930 года; оно принадлежит переводчику — Вернеру Блоху — 15 августа 1930 года.) Книга стала вехой в развитии квантовой механики, систематически устанавливая четкий формализм для выполнения вычислений, и среди прочего, объясняя предсказание Дирака о позитроне, который будет открыт в 1932 году.
Почему у Алана Тьюринга была книга на немецком, а не на английском? Я не знаю этого точно, но в те дни немецкий язык был ведущим языком науки, и мы знаем, что Алан Тьюринг умел на нем читать. (В конце концов, в названии его знаменитой машинной работы Тьюринга «О вычислимых числах с приложением к Проблеме разрешения (Entscheidungsproblem)» было очень длинное немецкое слово — и в основной части статьи он оперирует довольно непонятными готическими символами в виде «немецких букв», которые он использовал, взамен, например, греческих символов).
Алан Тьюринг купил эту книгу сам или ему ее передали? Я не знаю. На внутренней стороне обложки книги Тьюринга есть карандашное обозначение »20/-», которое было стандартным обозначением »20 шиллингов», аналогично £1. На правой странице есть стёртое »26.9.30», предположительно означающее 26 сентября 1930 года — возможно, дату, когда книга была впервые приобретена. Затем, в крайнем правом углу, стертая цифра »20». Возможно, это снова цена. (Может ли это быть цена в рейхсмарках, если предположить, что книга была продана в Германии? В те времена 1 рейхсмарка стоила примерно 1 шиллинг, немецкая цена, вероятно, была бы записана как, например,»20 RM».) Наконец, на внутренней стороне задней обложки есть «c 5/-» — может быть это, (с большой скидкой) цена за книгу, бывшую в употреблении.
Давайте рассмотрим основные даты жизни Алана Тьюринга. Алан Тьюринг родился 23 июня 1912 года (по совпадению, ровно за 76 лет до выпуска Mathematica 1.0). Осенью 1931 года он поступил в Королевский колледж в Кембридже. Он получил степень бакалавра после стандартных трех лет обучения, в 1934 году.
В 1920-х и начале 1930-х годов квантовая механика была животрепещущей темой, и Алан Тьюринг безусловно интересовался ей. Из его архивов мы знаем, что в 1932 году, как только книга была опубликована, он получил «Математические основы квантовой механики» Джона фон Неймана (на немецком языке). Нам также известно, что в 1935 году Тьюринг получил задание от кембриджского физика Ральфа Фаулера по тематике изучения квантовой механики. (Фаулер предложил вычислить диэлектрическую проницаемость воды, что на самом деле является очень сложной задачей, требующей полноценного анализа с взаимодействующей квантовой теорией поля, которая до сих пор является не полностью решенной).
И все же, когда и как Тьюринг заполучил свой экземпляр книги Дирака? Учитывая, что на книге есть пробитая цена, Тьюринг предположительно купил ее уже подержанной. Кто же был первым владельцем книги? Заметки в книге, кажется, касаются в первую очередь логической структуры, отмечается, что некоторую логическую взаимосвязь следует считать аксиомой. Тогда как же насчет записки, вложенной на странице 127?
Что ж, возможно это совпадение, но как раз на странице 127 — Дирак говорит о квантовом принципе наименьшего действия и закладывает основу для интеграла по пути Фейнмана — что является основой всего современного квантового формализма. Что содержится в записке? Там содержится расширение уравнения 14, которое является уравнением для временной эволюции квантовой амплитуды. Автор записки заменил Дираковскую А для амплитуды на ρ, возможно, отражая тем самым более раннюю (аналогия плотности жидкости) немецкую запись. Затем автор пытается расширить действие по степеням ℏ (постоянная Планка, деленная на 2π, которую иногда называют постоянной Дирака).
Но, похоже, из того, что содержится на странице, можно мало что почерпнуть полезного. Если держать страницу на свету, в ней содержится небольшой сюрприз — водяной знак с надписью «Z f. Physik. Chem. B»:

Это сокращенная версия Zeitschrift für physikalische Chemie, Abteilung B — немецкого журнала по физической химии, который стал издаваться с 1928 года. Возможно, записка была написана редактором журнала? Вот заголовок журнала за 1933 год. Удобно, что редакторы перечислены с указанием их местожительства, и один из них выделяется: «Борн · Кембридж».

Это и есть Макс Борн который является автором правила Борна и много чего еще другого в теории квантовой механики (а также дедушкой певицы Оливии Ньютон-Джон). Итак, эта записка, возможно, была написана Максом Борном? Но, к сожалению, это не так, потому что почерк не совпадает.
А как насчет закладки на странице 231? Вот она с двух сторон:

Закладка является странной и довольно красивой. Но когда она была изготовлена? В Кембридже существует книжный магазин Хефферса, хотя теперь он является частью Блэквелла. В течение более 70 лет (до 1970 года) Хефферс находился по адресу, как показывает закладка, 3 и 4 по Petty Cury.
В данной закладке находится важный ключ — это номер телефона «Тел. 862». Так вышло, что в 1939 году большая часть Кембриджа (включая Хефферс) перешла на четырехзначные номера, и, безусловно, к 1940 году закладки печатались с «современными» телефонными номерами. (Английские телефонные номера постепенно становились все длиннее; когда я рос в Англии в 1960-х годах, наши телефонные номера были «Оксфорд 56186» и «Кидмор-Энд 2378». Отчасти я помню эти цифры потому, что, как бы странно это теперь не выглядело, я всегда называл свой номер при ответе на входящий звонок).
Закладка в таком виде печаталась до 1939 года. Но как задолго до этого? В Интернете можно найти довольно много сканов старых рекламных объявлений Heffers, по крайней мере, с 1912 года (наряду с «Мы просим вас удовлетворить ваши запросы…») они дописывают «Телефон 862», добавляя »(2 строки)». Также существует некоторые закладки с похожим оформлением, которые можно найти в книгах еще с 1904 года (хотя неясно, были ли они оригинальными для этих книг (то есть напечатанными в тоже время). В целях нашего расследования, кажется, мы можем сделать вывод, что данная книга пришла из магазина Хефферс (который, кстати, был главным книжным магазином в Кембридже) где-то между 1930 и 1939 годами.
Страница с лямбда-исчислениями
Итак, теперь мы знаем кое-что о том, когда же книга была куплена. Но как насчет «страницы с лямбда-исчислениями»? Когда это было написано? Ну, естественно к тому времени лямбда-исчисление должно было быть уже изобретено. И это было сделано Алонзо Черчем, математиком из Принстона, в первоначальной форме в 1932 году и в окончательной форме в 1935 году. (Существовали работы ученых предшественников, но они не использовали обозначение λ).
Существует сложная связь между Аланом Тьюрингом и лямбда-исчислением. В 1935 году Тьюринг заинтересовался «механизацией» математических операций, и изобрел идею машины Тьюринга с использованием ее для решения задач основ математики. Тьюринг отправил статью на эту тему во французский журнал (Comptes rendus), но она был утеряна на почте;, а потом оказалось, что адресата, которому он послал ее, все равно не было на месте, поскольку он переехал Китай.
Но в мае 1936 года, еще до того как Тьюринг мог отправить свою статью куда-либо еще, из США прибыла работа Алонзо Черча. Тьюринг до этого уже сетовал на то, что когда в 1934 году он разработал доказательство центральной предельной теоремы, то обнаружил, что существует норвежский математик, который уже представил доказательство в 1922 году.
Нетрудно понять, что машины Тьюринга и лямбда-исчисление фактически эквивалентны в тех видах вычислений, которые они могут представлять (и это является началом тезиса Черча-Тьюринга). Однако Тьюринг (и его учитель Макс Ньюман) убедились, что подход Тьюринга был достаточно отличным для того, чтобы это заслуживало отдельной публикации. В ноябре 1936 года (а с исправленными опечатками в следующем месяце) в трудах Лондонского математического общества была опубликована знаменитая статья Тьюринга «О вычислимых числах…».
Чтобы немного восполнить временную шкалу: с сентября 1936 года по июль 1938 года (с перерывом в три месяца летом 1937 года) Тьюринг находился в Принстоне, поехав туда, с целью стать аспирантом Алонзо Черча. В этот период в Принстоне Тьюринг, по-видимому, полностью сконцентрировался на математической логике — написал несколько трудных для чтения статей, полных лямбда-исчислениями Черча, — и, скорее всего, у него не было с собой книги по квантовой механике.
Тьюринг вернулся в Кембридж в июле 1938 года, но уже к сентябрю того же года он работал на полставки в Правительственной школе кодов и шифров, а год спустя он переехал в Блетчли-Парк, с целью работать там полный рабочий день над вопросами, связанными с криптоанализом. После окончания войны в 1945 году Тьюринг переехал в Лондон для того, чтобы работать в Национальной физической лаборатории над разработкой проекта создания компьютера. 1947–8 учебный год он провел в Кембридже, но затем переехал в Манчестер для того, чтобы разработать там первый компьютер.
В 1951 году Тьюринг начал серьезно заниматься теоретической биологией. (Лично для меня данный факт является в некотором роде ироничным, потому как мне кажется, что Тьюринг всегда подсознательно считал, что биологические системы должны моделироваться дифференциальными уравнениями, а не чем-то дискретным, как машины Тьюринга или клеточные автоматы). Также он снова обратил свой интерес к физике, и к 1954 году даже написал своему другу и ученику Робину Гэнди, что:»я пытался изобрести новую квантовую механику» (хотя он добавил:»но на самом деле не факт, что получится»). Но, к сожалению, все внезапно оборвалось 7 июня 1954 года, когда Тьюринг внезапно умер. (Я полагаю, что это не было самоубийством, но это уже совсем другая история.)
Итак, вернемся к странице лямбда-исчисления. Поднесем ее к свету, и снова увидим водяной знак:

Видно, что это листок бумаги британского производства, и мне кажется маловероятным, чтобы его использовали в Принстоне. Но можем ли мы точно датировать его? Что ж, не без некоторой помощи Британской ассоциации историков производителей бумаги, мы знаем, что официальным производителем бумаги были Spalding&Hodge, Papermakers, оптовые и экспортные компании «Друри Хауз», Рассел-стрит в районе Друри Лейн, Ковент-Гарден, Лондон. Это может нам помочь, но не очень сильно, так как можно предположить, что их марка бумаги Excelsior, кажется, была включена в каталоги поставки с 1890-х по 1954 год.
О чем говорится в этой страничке?

Итак, давайте рассмотрим более подробно, что находится на двух сторонах листочка. Начнем с лямбд.
Здесь представлен способ определения «чистых» или «анонимных» функций, и они являются основным понятием в математической логике, а сейчас и в функциональном программировании. Эти функции достаточно распространены в языке Wolfram Language, и их задание довольно легко объяснить. Например, кто-то пишет f[x], чтобы обозначить функцию f, примененную к аргументу x. И есть много именованных функций f таких как Abs или Sin или Blur. Но что, если кто-то захочет, чтобы f[x] было 2x +1? Здесь нет непосредственного названия (имени) для этой функции. Но существует ли другая форма задания, f[x]?
Ответ да: вместо f мы пишем Function[a,2a+1]. А на языке Wolfram Function [a,2a+1][x] применяет функции к аргументу x, выдавая в итоге 2x+1. Function[a,2a+1] является «чистой» или «анонимной» функцией, которая представляет собой чистую операцию умножения на 2 и прибавления 1.
Итак, λ в лямбда-исчислении является точным аналогом Function в языке Wolfram Language — и поэтому, например, λa.(2 a+1) эквивалентно Function[a, 2a + 1]. (Стоит отметить, что функция, скажем, Function[b,2b+1] эквивалентна; «связанные переменные» a или b являются просто местами подстановки аргумента функции —, а в языке Wolfram Language их можно избежать, используя альтернативные варианты определения чистой функции (2# +1)&).
В традиционной математике функции обычно рассматриваются как объекты, которые отображают входные данные (например, целые числа) и выходные данные (которые также являются, например, целыми числами). Но что это за объект Function (или λ)? По сути это есть структурный оператор, который принимает выражения и превращает их в функции. Это может показаться немного странным с точки зрения традиционной математики и математической формы записи, но если кому-то необходимо выполнять манипулирование произвольными символами, что гораздо более естественно, даже если сначала это кажется немного абстрактным. (Следует отметить, что когда пользователи изучают язык Wolfram Language, я всегда могу сказать, что они преодолели определенный порог абстрактного мышления, когда они получают представление о Function).
Лямбды — это только часть того, что присутствует на странице. Есть и другая, еще более абстрактная концепция — это комбинаторы. Рассмотрим довольно неясную строку PI1IIx? Что это может значить? По сути, это последовательность комбинаторов, или, некая абстрактная композиция символьных функций.
Обычную суперпозицию функций, довольно знакомую по математике, на языке Wolfram Language можно записать в виде: f[g[x]] — что означает «применить f к результату применения g к x». Но действительно ли нужны для этого скобки? На языке Wolfram f@g@ x — альтернативная форма записи. В этой записи мы полагаемся на определение в языке Wolfram Language: оператор @ ассоциируется с правой частью, поэтому f@g@x эквивалентно f@(g@x).
Но что будет означать запись (f@g)@x? Это эквивалентно f[g][x]. И если бы f и g были обычными функциями в математике, это было бы бессмысленно, но если f — функция высшего порядка, то f[g] сама по себе может быть функцией, которая вполне может быть применена к x.
Отметим здесь есть еще некоторую сложность. В f[х] — f является функцией одного аргумента. И f[х] эквивалентно записи Function[a, f[a]][x]. Но как быть в случае функции двух аргументов, скажем, f[x,y]? Это может быть записано в виде Function[{a,b},f[a, b]][x, y]. Но как быть в случае Function[{a},f[a,b]]? Что это? Здесь присутствует «свободная переменная» b, которая просто передается в функцию. Function[{b},Function[{a},f[a,b]]] свяжет эту переменную, а затем Function[{b},Function[{a},f [a, b]]][y][x] дает f[x,y] снова. (Задание функции так, чтобы она имела один аргумент, называется «каррирование» в честь ученого логика по имени Хаскелл Карри).
Если существуют свободные переменные, то есть много различных сложностей относительно того, как функции могут быть заданы, но если мы ограничимся объектами Function или λ, которые не имеют свободных переменных, то они в основном могут быть заданы свободно. Такие объекты называются комбинаторами.
Комбинаторы имеют длинную историю. Известно, что они были впервые предложены в 1920 году учеником Дэвида Гилберта — Моисеем Шенфинкелем.
В ту пору, только совсем недавно было обнаружено, что не нужно использовать выражения And, Or и Not для представления выражений в стандартной логике высказываний: достаточно было использовать единственный оператор, который мы теперь будем называть Nand (потому что, например, если писать Nand как ·, то Or[a,b] примет вид (a·a)·(b·b)). Шенфинкель хотел найти такое же минимальное представление логики предикатов или, по сути, логики, включая функции.
Он придумал два «комбинатора» S и K. В языке Wolfram Language это запишется в виде
K[x_][y_] → x и S[x_][y_][z_] → x[z][y[z]].
Является примечательным, что оказалось возможным использовать эти два комбинатора для выполнения любых вычислений. Так, например,
S[K[S]][S[K[S[K[S]]]][S[K[K]]]]
можно использовать как функцию для добавления двух целых чисел.
Все это, мягко говоря, довольно абстрактные объекты, но теперь, когда мы понимаем, что такое машины Тьюринга и лямбда-исчисление, можно увидеть, что комбинаторы Шенфинкеля фактически предвосхитили концепцию универсальных вычислений. (И что еще более примечательно, определения S и K 1920 года минимально просты, и напоминают очень простую универсальную машину Тьюринга, которую я предложил в 1990-х годах, универсальность которой была доказана в 2007 году).
Но вернемся к нашему листочку и строке PI1IIx. Символы, записанные здесь, являются комбинаторами, и все они предназначены для задания функции. Здесь определение заключается в том, что суперпозиция функций должна быть левоассоциативной, так что fgx следует трактовать не как f@g@x или f@(g@x) или f[g[x]], а скорее, как (f@g)@x или f[g][x]. Переведем эту запись в вид, удобный для использования Wolfram Language: PI1IIx примет вид p[i][one][i][i][x].
Зачем писать что-то подобное? Для того, чтобы объяснить это, нам необходимо обсудить понятие цифр Черча (названных в честь Алонзо Черча). Допустим, мы просто работаем с символами и с лямбдами или комбинаторами. Существует ли способ использовать их для задания целых чисел?
Как насчет того, чтобы просто сказать, что число n соответствует Function[x, Nest[f,x,n]]? Или, другими словами, что (в более коротких обозначениях):
1 — это f[#]&
2 — это f[f[#]]&
3 — это f[f[f[#]]]& и так далее.
Все это может показаться несколько более неясным, но причина, по которой это представляет интерес, в том, что она позволяет нам делать все полностью символьным и абстрактным, без необходимости явно говорить о чем-то типа целых чисел.
При таком методе задания чисел, представим себе, например, добавление двух чисел: 3 можно представить в виде f[f[f[#]]]& и 2 — это f[f[#]]&. Можно сложить их, просто применив одно из них к другому:
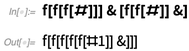
Но что же из себя представляет объект f? Это может быть все что угодно! В некотором смысле, «переходить к lambda» до конца и представлять числа с помощью функций, которые принимают f в качестве аргумента. Другими словами, представим 3, например, как Function[f,f[f[f[#]]] &] или Function[f,Function[x,f[f[f[x]]]]. (когда и как вам необходимо называть переменные — загвоздка в лямбда-исчислении).
Рассмотрим фрагмент статьи Тьюринга 1937 года «Вычислимость и λ- диффинируемость», которая настраивает объекты именно так, как мы только что обсуждали:

Здесь запись может несколько сбить с толку. x Тьюринга — это наша f, а его x' (наборщик совершил ошибку вставив пробел) — это наш x. Но здесь используется точно такой же подход.
Итак, давайте посмотрим на строку сразу после сгиба в передней части листка. Это I1IIYI1IIx. По форме записи Wolfram Language это будет i[one][i][i][y][i][one][i][i][x]. Но здесь i — тождественная функция, поэтому i[one] выдает просто one. Между тем, one — это числовое представление Черча для 1 или Function[f,f[#]&]. Но с этим определением one[а] становится a[#]& и one[a][b] становится a[b]. (Кстати, i[а][b], или Identity[а][b] также является а[b]).
Будет намного понятнее, если мы запишем правила замены для i и one, вместо прямого применения лямбда-исчисления. Результат будет такой же. Примените эти правила явно, мы получим:

И это точно то же самое, что представлено на первой сокращенной записи:
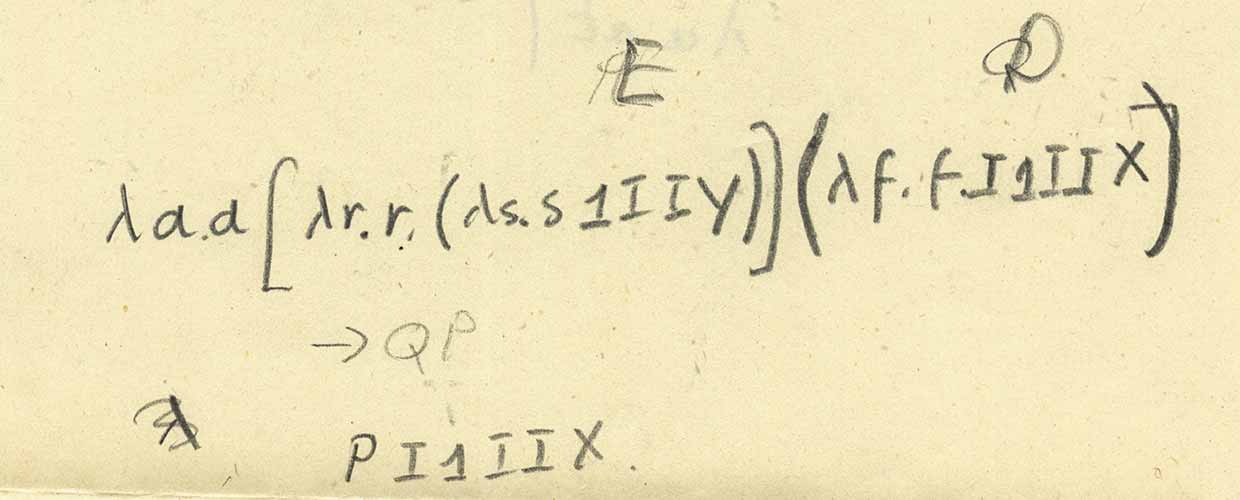
Давайте теперь посмотрим на листок снова, в его верхнюю часть:
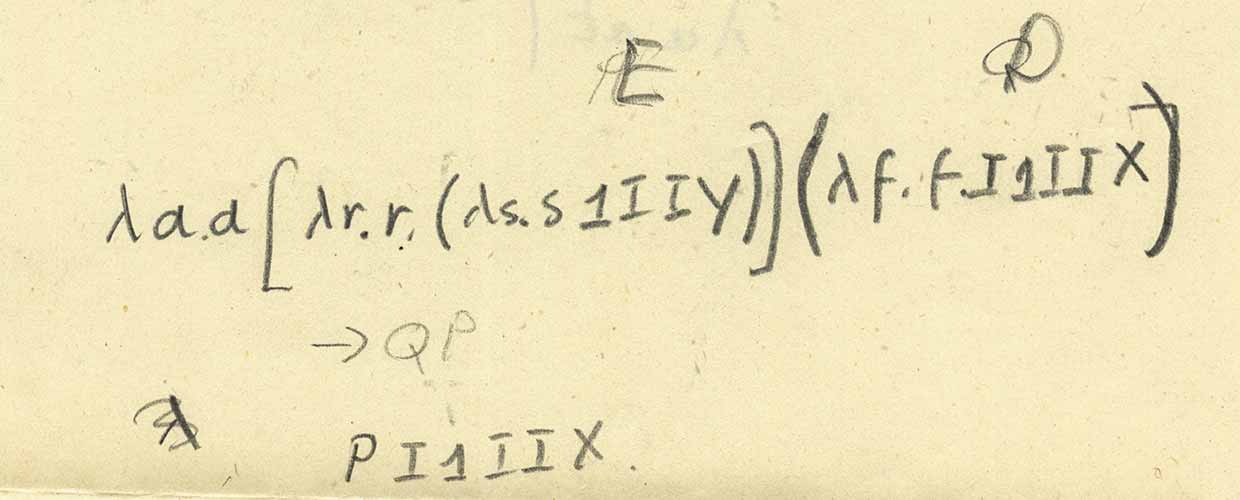
Здесь присутствуют довольно запутанные и непонятные объекты «E» и «D», но под ними имеется в виду «P» и «Q», поэтому мы можем выписать выражение и вычислить его (обратите внимание, что здесь — после некоторой путаницы с самым последним символом — «таинственный ученый» ставит […] и (…) для представления приложения функции):

Итак, это первое показанное сокращение. Чтобы увидеть больше, давайте подставим определения для Q:

Мы получаем точно следующее показанное сокращение. Что будет если подставить выражения для P?
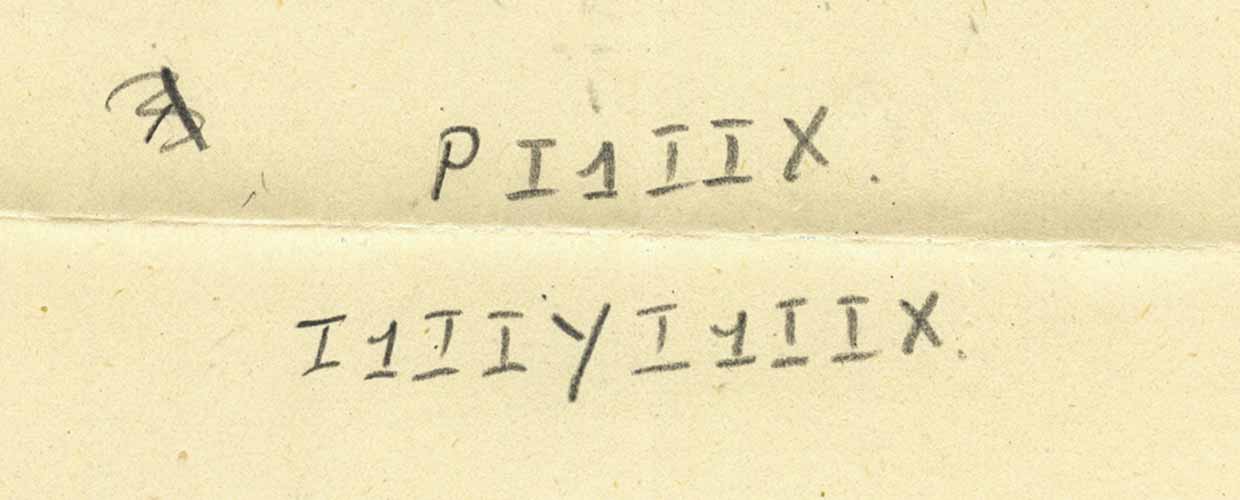
Вот результат:

И теперь, используя тот факт, что i — это функция, выдающая на выходе сам аргумент, мы получаем:

Оооопс! Но это же не следующая записанная строка. Есть ли тут ошибка? Непонятно. Потому что, в конце концов, в отличие от большинства других случаев, нет стрелки, указывающей, что следующая строка следует из предыдущей.
Здесь какая-то загадка, но давайте перейдем к нижней части листка:
Здесь 2 — это число Черча, определяемое, например, шаблоном two[a_] [b_] → a[a[b]]. Обратите внимание, что это на самом деле форма второй строки, если a рассматривать как Function[r,r[р]] и b как q. Итак, мы ожидаем, что результат вычислений будет следующим:

Тем не менее, лежащее внутри выражение а[b] может быть записано как x (вероятно, отличается от x ранее записанного на листке) — в итоге получим окончательный результат:

Итак, мы можем расшифровать немногое из того, что происходит на этом листке, но по крайней мере одна загадка, которая до сих пор остается, — это то, чем должен быть Y.
На самом деле в комбинаторной логике есть стандартный Y-комбинатор: так называемый комбинатор с фиксированной точкой. Формально он определяется тем, что Y[f] должно быть равно f[Y[f]], или, другими словами, что Y[
