[Перевод] Кластеризуем лучше, чем «метод локтя»

Кластеризация — важная часть конвейера машинного обучения для решения научных и бизнес-задач. Она помогает идентифицировать совокупности тесно связанных (некой мерой расстояния) точек в облаке данных, определить которые другими средствами было бы трудно.
Однако процесс кластеризации по большей части относится к сфере машинного обучения без учителя, для которой характерен ряд сложностей. Здесь не существует ответов или подсказок, как оптимизировать процесс или оценить успешность обучения. Это неизведанная территория.
Поэтому неудивительно, что популярный способ кластеризации методом k-среднего не даёт полностью удовлетворяющего нас ответа на вопрос: «Как нам сначала узнать количество кластеров?» Этот вопрос крайне важен, потому что кластеризация часто предшествует дальнейшей обработке отдельных кластеров, и от оценки их количества может зависеть объём вычислительных ресурсов.
Худшие последствия могут возникать в сфере бизнес-анализа. Здесь кластеризация применяется для сегментации рынка, и возможно, что сотрудников маркетинга будут выделять в соответствии с количеством кластеров. Поэтому ошибочная оценка этого количества может привести к неоптимальному распределению ценных ресурсов.
При кластеризации методом k-средних количество кластеров чаще всего оценивают с помощью «метода локтя». Он подразумевает многократное циклическое исполнение алгоритма с увеличением количества выбираемых кластеров, а также последующим откладыванием на графике балла кластеризации, вычисленного как функция от количества кластеров.
Что это за балл, или метрика, которая откладывается на графике? Почему называют методом локтя?
Характерный график выглядит так:
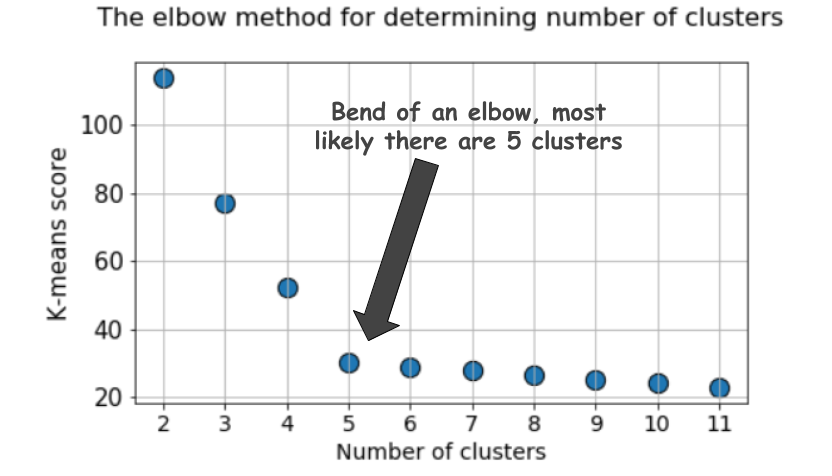
Балл, как правило, является мерой входных данных по целевой функции k-средних, то есть некой формой отношения внутрикластерного расстояния к межкластерному расстоянию.
Например, этот метод балльной оценки сразу доступен в средстве оценки по методу k-средних в Scikit-learn.
Но взгляните ещё раз на этот график. В нём чувствуется что-то странное. Какое оптимальное количество кластеров у нас получилось, 4, 5 или 6?
Непонятно, не правда ли?
Коэффициент «силуэт» вычисляется с помощью среднего внутрикластерного расстояния (a) и среднего расстояния до ближайшего кластера (b) по каждому образцу. Силуэт вычисляется как (b - a) / max(a, b). Поясню: b — это расстояние между a и ближайшим кластером, в который a не входит. Можно вычислить среднее значение силуэта по всем образцам и использовать его как метрику для оценки количества кластеров.
Вот видео, в котором объясняется эта идея:
Допустим, мы сгенерировали случайные данные с помощью функции make_blob из Scikit-learn. Данные расположены в четырёх измерениях и вокруг пяти кластерных центров. Суть проблемы в том, что данные сгенерированы вокруг пяти кластерных центров. Однако алгоритм k-средних об этом не знает.
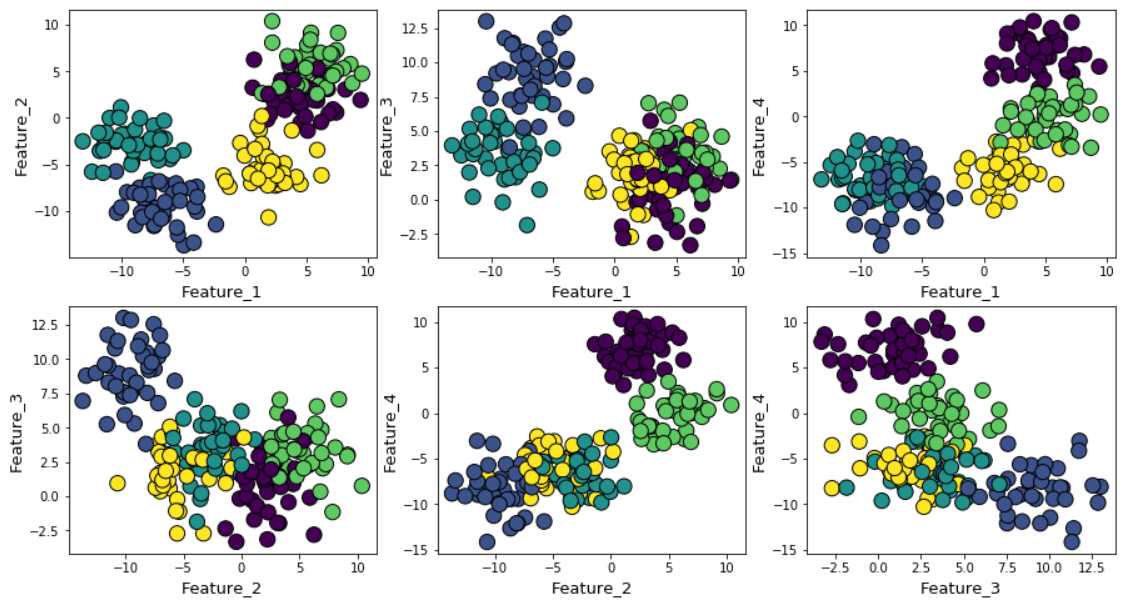
Кластеры можно отобразить на графике следующим образом (попарные признаки):
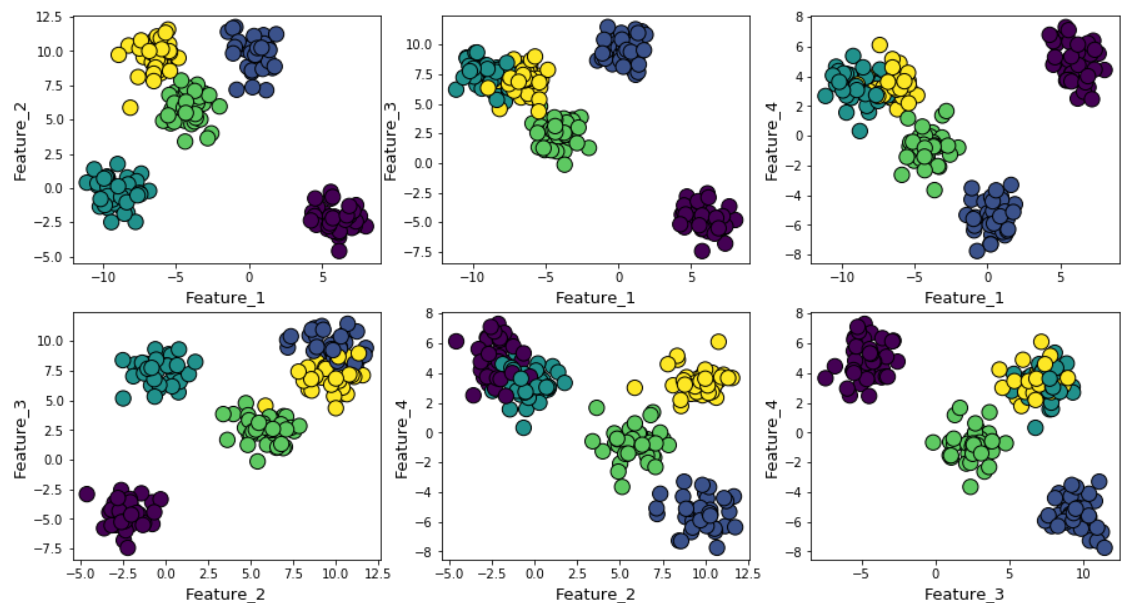
Затем прогоним алгоритм k-средних со значениями от k=2 до k=12, а затем вычислим метрику по умолчанию к k-средних и среднее значение силуэта для каждого прогона, с выводом результатов в двух соседних графиках.
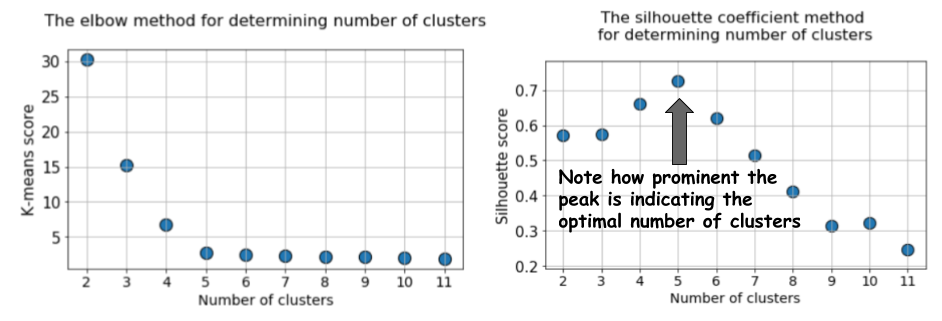
Разница очевидна. Среднее значение силуэта возрастает до k=5, а затем резко снижается для более высоких значений k. То есть мы получаем выраженный пик при k=5, это количество кластеров, сгенерированных в исходном датасете.
График силуэта имеет пиковый характер, в отличие от мягко изогнутого графика при использовании метода локтя. Его проще визуализировать и обосновать.
Если увеличить гауссов шум при генерировании данных, то кластеры будут сильнее накладываться друг на друга.
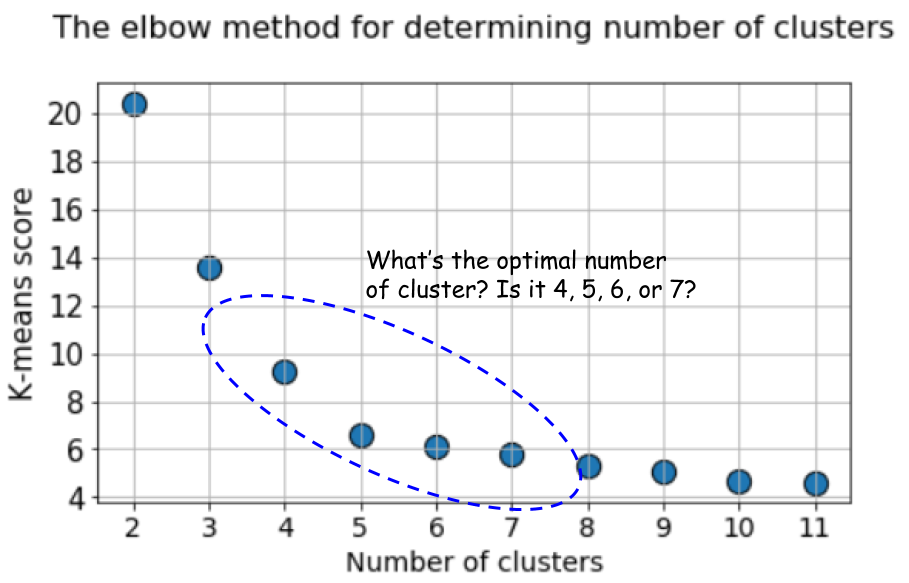
В этом случае вычисление k-средних по умолчанию с применением метода локтя даёт ещё более неопределённый результат. Ниже показан график метода локтя, на котором трудно выбрать подходящую точку, в которой линия на самом деле изгибается. Это 4, 5, 6 или 7?
При этом график силуэта всё ещё демонстрирует пик в районе 4 или 5 кластерных центров, что существенно облегчает нам жизнь.
Если вы посмотрите на накладывающиеся друг на друга кластеры, то увидите, что, несмотря на то, что мы сгенерировали данные вокруг 5 центров, из-за высокой дисперсии структурно можно выделить только 4 кластера. Силуэт легко выявляет это поведение и показывает оптимальное количество кластеров между 4 и 5.

Есть и другие замечательные метрики для определения истинного количества кластеров, например, байесовский информационный критерий (BIC). Но их можно применять лишь в том случае, если нам нужно перейти от метода k-средних к более обобщённой версии — смеси нормальных распределений (Gaussian Mixture Model (GMM)).
GMM рассматривает облако данных как суперпозицию многочисленных датасетов с нормальным распределением, с отдельными средними значениями и дисперсиями. А затем GMM применяет алгоритм максимизации ожиданий, чтобы определить эти средние и дисперсии.

BIC для регуляризации
Вы уже могли сталкиваться с BIC в статистическом анализе или при использовании линейной регрессии. BIC и AIC (Akaike Information Criterion, информационный критерий Акаике) используются в линейной регрессии в качестве методик регуляризации для процесса отбора переменных.
Аналогичная идея применяется и в случае с BIC. Теоретически, крайне сложные кластеры можно смоделировать как суперпозиции большого количества датасетов с нормальным распределением. Для решения этой задачи можно применять неограниченное количество таких распределений.
Но это аналогично увеличению сложности модели в линейной регрессии, когда для соответствия данным любой сложности может использоваться большое количество свойств, лишь для того, чтобы потерять возможность обобщения, поскольку излишне сложная модель соответствует шуму, а не настоящему паттерну.
Метод BIC штрафует многочисленные нормальные распределения и пытается сохранить модель достаточно простой, чтобы она описывала заданный паттерн.
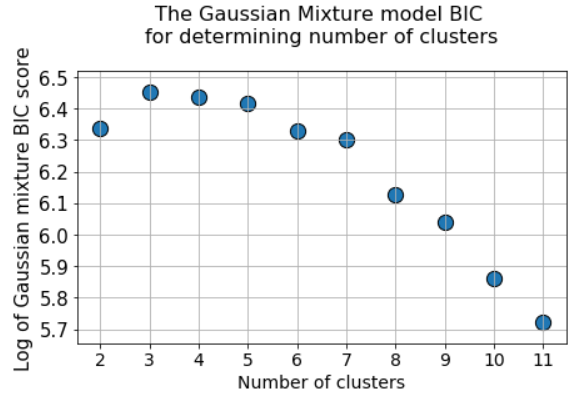
Следовательно, можно прогнать алгоритм GMM для большого количества кластерных центров, и значение BIC вырастет до какой-то точки, а затем начнёт снижаться по мере роста штрафа.
Вот Jupyter notebook для этой статьи. Можете свободно форкать и экспериментировать.
Мы обсудили пару альтернатив популярному методу локтя с точки зрения выбора правильного количества кластеров при обучении без учителя с применением алгоритма k-средних.
Мы убедились, что вместо метода локтя для визуального определения оптимального количества кластеров лучше использовать коэффициент «силуэт» и значение BIC (из GMM-расширения для k-средних).
