[Перевод] Карты из шестиугольников в Unity: неровности, реки и дороги
Начало: части 1–3.
Оглавление
- Сэмплируем текстуру шума.
- Перемещаем вершины.
- Сохраняем плоскостность ячеек.
- Подразделяем рёбра ячеек.
Пока наша сетка являлась строгим узором из сот. В этой части мы добавим неровности, чтобы карта выглядела естественнее.

Больше никаких ровных шестиугольников.
Шум
Чтобы добавить неровности, нам нужна рандомизация, но не истинная случайность. Мы хотим, чтобы при изменении карты всё оставалось согласованным. В противном случае при внесении любого изменения объекты будут скакать. То есть нам нужна некая форма воспроизводимого псевдослучайного шума.
Хорошим кандидатом является шум Перлина. Он воспроизводим в любой точке. При комбинировании нескольких частот он также создаёт шум, который может сильно варьироваться на больших расстояниях, но остаётся почти одинаковым на малых расстояниях. Благодаря этому можно создавать относительно плавные искажения. Находящиеся рядом друг с другом точки обычно остаются рядом, а не разбрасываются в противоположных направлениях.
Мы можем генерировать шум Перлина программно. В туториале Noise я объясняю, как это сделать. Но также мы можем выполнять сэмплирование из заранее сгенерированной текстуры шума. Преимущество использования текстуры заключается в том, что это проще и намного быстрее, чем вычисление многочастотного шума Перлина. Её недостаток в том, что текстура занимает больше памяти и покрывает только небольшую область шума. Поэтому она должна быть бесшовно соединяющейся и достаточно большой, чтобы повторения не бросались в глаза.
Текстура шума
Мы воспользуемся текстурой, поэтому туториал Noise вам изучать необязательно. Значит, нам нужна текстура. Вот она:

Бесшовно соединяемая текстура шума Перлина.
Показанная выше текстура содержит бесшовно соединяемый многочастотный шум Перлина. Это изображение в оттенках серого. Его среднее значение равно 0.5, а крайние значения стремятся к 0 и 1.
Но постойте, на каждую точку приходится только одно значение. Если нам нужно трёхмерное искажение, то потребуется как минимум три псевдослучайных сэмпла! Поэтому нам необходимы ещё две текстуры с разным шумом.
Мы можем создать их или хранить разные значения шума в каждом из цветовых каналов. Это позволит нам хранить до четырёх паттернов шума в одной текстуре. Вот эта текстура.

Четыре в одном.
Скачайте эту текстуру и импортируйте её в проект Unity. Так как мы собираемся сэмплировать текстуру через код, она должна быть читаемой. Переключите Texture Type на Advanced и включите Read/Write Enabled. Это сохранит данные текстуры в памяти и к ним можно будет получить доступ из кода на C#. Задайте для Format значение Automatic Truecolor, иначе ничего не сработает. Мы не хотим, чтобы сжатие текстур уничтожило наш паттерн шума.
Можно отключить Generate Mip Maps, потому что они нам не потребуются. Также включите Bypass sRGB Sampling. Это нам не понадобится, но так будет правильно. Этот параметр обозначает, что текстура не содержит данных цвета в гамма-пространстве.
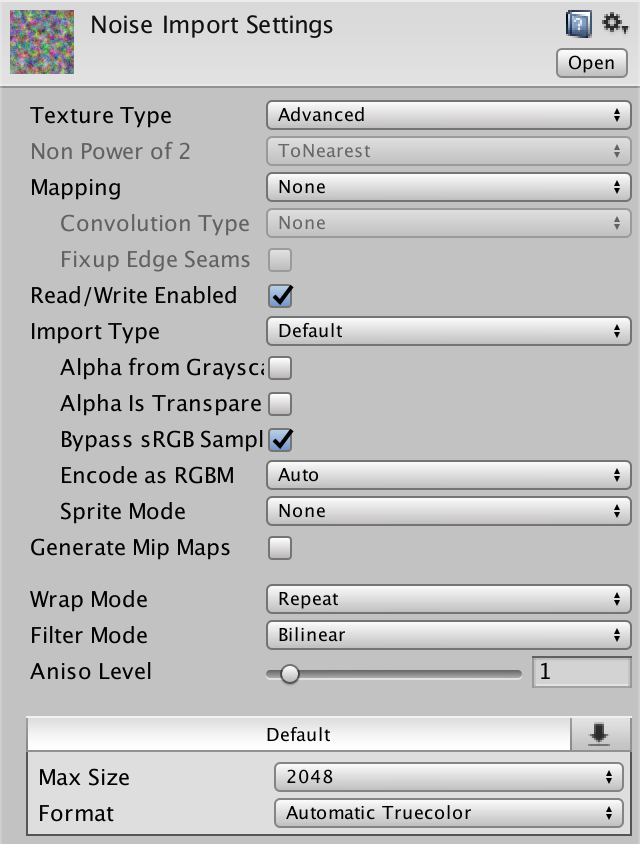

Импортированная текстура шума.
Если бы мы хотели использовать текстуру в шейдере, то это имело бы значение. При использовании режиме Linear rendering сэмплирование текстуры автоматически преобразует цветовые данные из гаммы в линейное цветовое пространство. В случае нашей текстуры шума это приведёт к неверным результатам, поэтому нам этого не нужно.
Их изменили после того, как был написан этот туториал. Нужно использовать настройки 2D-текстуры по умолчанию, sRGB (Color Texture) должно быть отключено, а для Compression должно быть задано значение None.
Сэмплирование шума
Давайте добавим функционал сэмплирования шума в HexMetrics, чтобы можно было использовать его в любом месте. Это значит, что HexMetrics должен содержать ссылку на текстуру шума.
public static Texture2D noiseSource;
Так как это не компонент, мы не можем назначить ему текстуру через редактор. Поэтому в качестве посредника мы используем HexGrid. Так как HexGrid будет действовать первым, будет вполне нормально, если мы передадим текстуру в начале его метода Awake.
public Texture2D noiseSource;
void Awake () {
HexMetrics.noiseSource = noiseSource;
…
}
Однако такой подход не переживёт рекомпиляции в режиме Play. Статические переменные не сериализуются движком Unity. Чтобы решить эту проблему, переназначим текстуру и в методе события OnEnable. Этот метод будет вызываться после рекомпиляции.
void OnEnable () {
HexMetrics.noiseSource = noiseSource;
}
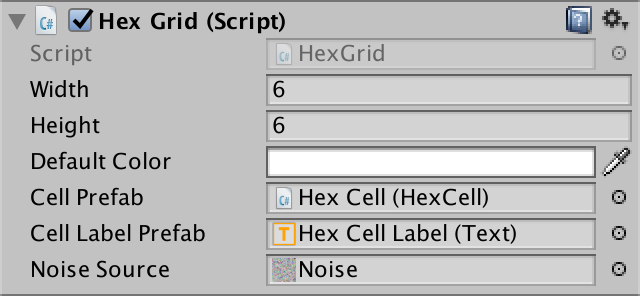
Назначаем текстуру шума.
Теперь, когда HexMetrics имеет доступ к текстуре, давайте добавим к нему удобный метод сэмплирования шума. Этот метод получает позицию в мире и создаёт 4D-вектор, содержащий четыре сэмпла шума.
public static Vector4 SampleNoise (Vector3 position) {
}
Сэмплы созданы сэмплированием текстуры с помощью билинейной фильтрации, при которой в качестве UV-координат использовались координаты мира X и Z. Так как наш источник шума двухмерный, мы игнорируем третью координату мира. Если бы источник шума был трёхмерным, мы бы использовали и координату Y.
В результате мы получаем цвет, который можно преобразовать в 4D-вектор. Такое приведение может быть косвенным, то есть мы можем вернуть непосредственно цвет, не включая явным образом (Vector4).
public static Vector4 SampleNoise (Vector3 position) {
return noiseSource.GetPixelBilinear(position.x, position.z);
}
unitypackage
Перемещение вершин
Мы исказим нашу ровную сетку из сот, по отдельности переместив каждую из вершин. Для этого давайте добавим к HexMesh метод Perturb. Он берёт неперемещённую точку и возвращает перемещённую. Для этого он использует неперемещённую точку при сэмплировании шума.
Vector3 Perturb (Vector3 position) {
Vector4 sample = HexMetrics.SampleNoise(position);
}
Давайте просто сложим сэмплы шума X, Y и Z непосредственно с соответствующими координатами точки и используем это как результат.
Vector3 Perturb (Vector3 position) {
Vector4 sample = HexMetrics.SampleNoise(position);
position.x += sample.x;
position.y += sample.y;
position.z += sample.z;
return position;
}
Как нам быстро изменить HexMesh, чтобы переместились все вершины? Изменением каждой вершины при добавлении в список вершин в методах AddTriangle и AddQuad. Давайте так и сделаем.
void AddTriangle (Vector3 v1, Vector3 v2, Vector3 v3) {
int vertexIndex = vertices.Count;
vertices.Add(Perturb(v1));
vertices.Add(Perturb(v2));
vertices.Add(Perturb(v3));
…
}
void AddQuad (Vector3 v1, Vector3 v2, Vector3 v3, Vector3 v4) {
int vertexIndex = vertices.Count;
vertices.Add(Perturb(v1));
vertices.Add(Perturb(v2));
vertices.Add(Perturb(v3));
vertices.Add(Perturb(v4));
…
}
Скорее всего нет. Они состоят из двух треугольников, которые больше не будут лежать в одной плоскости. Однако поскольку эти треугольники имеют две общих вершины, нормали этих вершин будут сглажены. Это значит, что у нас не будет резких переходов между двумя треугольниками. Если искажение не слишком велико, то мы по-прежнему будем воспринимать четырёхугольники плоскими.

Вершины то ли перемещены, то ли нет.
Пока изменения не очень заметны, только пропали метки ячеек. Это произошло потому, что мы добавили к точкам сэмплы шума, а они всегда являются положительными. Поэтому в результате все треугольники поднялись над своими метками, закрывая их. Мы должны отцентрировать изменения, чтобы они происходили в обоих направлениях. Сменим интервал сэмпла шума с 0–1 на −1–1.
Vector3 Perturb (Vector3 position) {
Vector4 sample = HexMetrics.SampleNoise(position);
position.x += sample.x * 2f - 1f;
position.y += sample.y * 2f - 1f;
position.z += sample.z * 2f - 1f;
return position;
}

Центрированные перемещения.
Величина (сила) перемещения
Теперь очевидно, что мы исказили сетку, но эффект едва заметен. Изменение составляет в каждом измерении не более 1 единицы. То есть теоретический максимум смещения равен √3 ≈ 1.73 единиц, что будет происходить чрезвычайно редко, если вообще произойдёт. Так как внешний радиус ячеек равен 10 единицам, то перемещения относительно малы.
Решение заключается в добавлении к HexMetrics параметра силы, чтобы можно было отмасштабировать перемещения. Давайте попробуем использовать силу 5. При этом теоретический максимум смещения будет равен √75 ≈ 8.66 единиц, что гораздо заметнее.
public const float cellPerturbStrength = 5f;
Применим силу, умножив её на сэмплы в HexMesh.Perturb.
Vector3 Perturb (Vector3 position) {
Vector4 sample = HexMetrics.SampleNoise(position);
position.x += (sample.x * 2f - 1f) * HexMetrics.cellPerturbStrength;
position.y += (sample.y * 2f - 1f) * HexMetrics.cellPerturbStrength;
position.z += (sample.z * 2f - 1f) * HexMetrics.cellPerturbStrength;
return position;
}

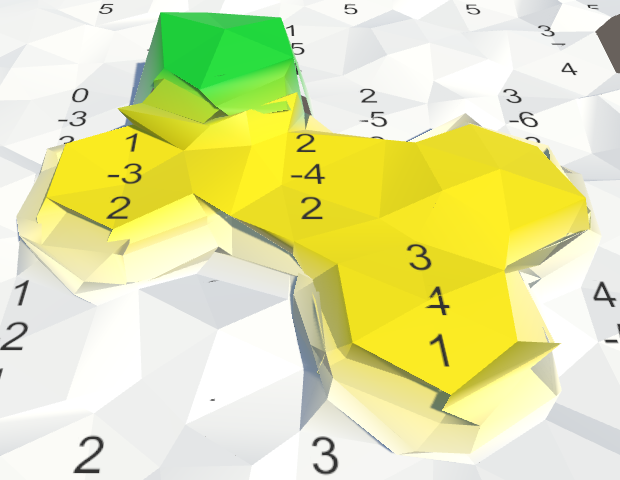
Увеличенная сила.
Масштаб шума
Хотя до изменения сетка выглядит хорошо, всё может пойти не так после появления уступов. Их вершины могут искажаться в непредсказуемо разных направлениях, создавая хаос. При использовании шума Перлина этого происходить не должно.
Проблема возникает потому, что для сэмплирования шума мы используем непосредственно координаты мира. Из-за этого текстура тайлится через каждую единицу, а ячейки гораздо больше этой величины. По сути, текстура сэмплируется в произвольных точках, разрушая существующую у неё целостность.
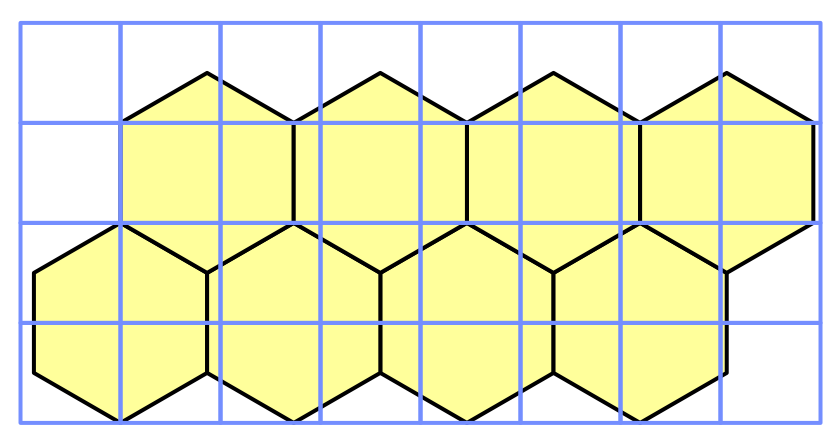
Строки сетки 10 на 10 перекрывают соты.
Нам придётся отмасштабировать сэмплирование шума, чтобы текстура покрывала гораздо бОльшую площадь. Давайте добавим этот масштаб в HexMetrics и присвоим ему значение 0.003, а затем отмасштабируем координаты сэмплов на этот коэффициент.
public const float noiseScale = 0.003f;
public static Vector4 SampleNoise (Vector3 position) {
return noiseSource.GetPixelBilinear(
position.x * noiseScale,
position.z * noiseScale
);
}
Внезапно оказывается, что наша текстура покрывает 333 ⅓ квадратных единиц, и её локальная целостность становится очевидной.
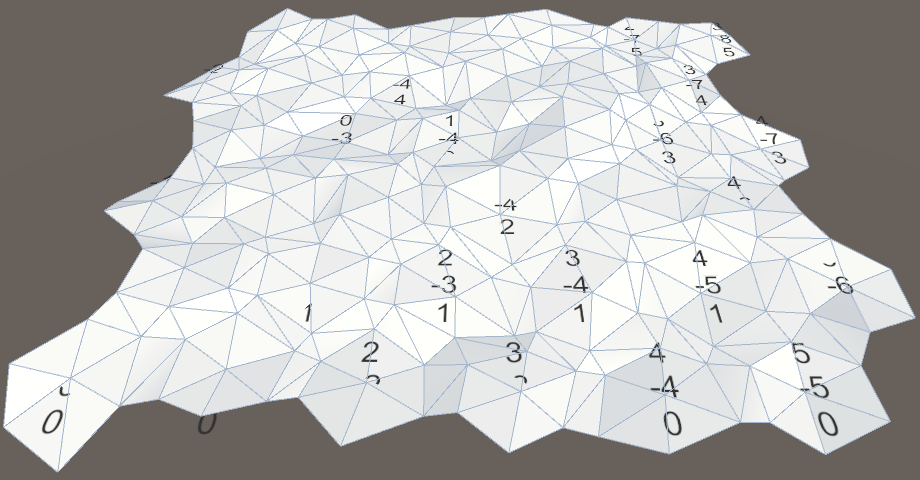
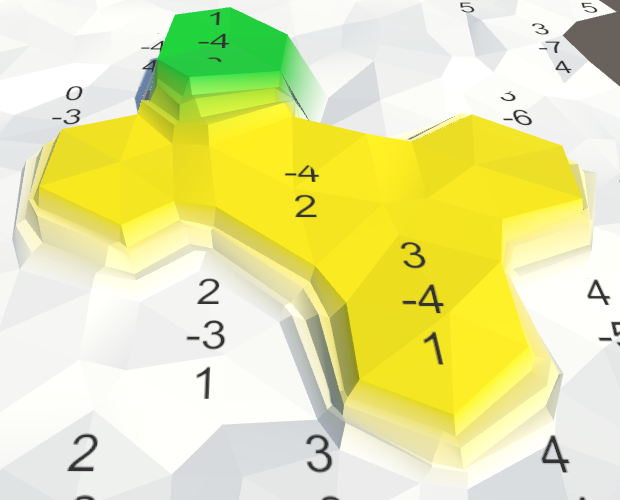
Отмасштабированный шум.
Кроме того, новый масштаб увеличивает расстояния между стыками шума. На самом деле, так как ячейки имеют внутренний диаметр 10√3 единиц, он никогда не будет ровно тайлиться в измерении X. Однако из-за локальной целостности шума, при бОльшем масштабе мы всё равно сможем распознать повторяющиеся паттерны, примерно через каждые 20 ячеек, даже если детали не будут совпадать. Но они будут очевидны только на карте без прочих характерных особенностей.
unitypackage
Выравнивание центров ячеек
Перемещение всех вершин придаёт карте более естественный вид, но возникает несколько проблем. Так как ячейки теперь неровные, их метки пересекаются с мешем. А в местах соединений уступов с обрывами возникают трещины. Трещины мы оставим на потом, а сейчас сосредоточимся на поверхностях ячеек.
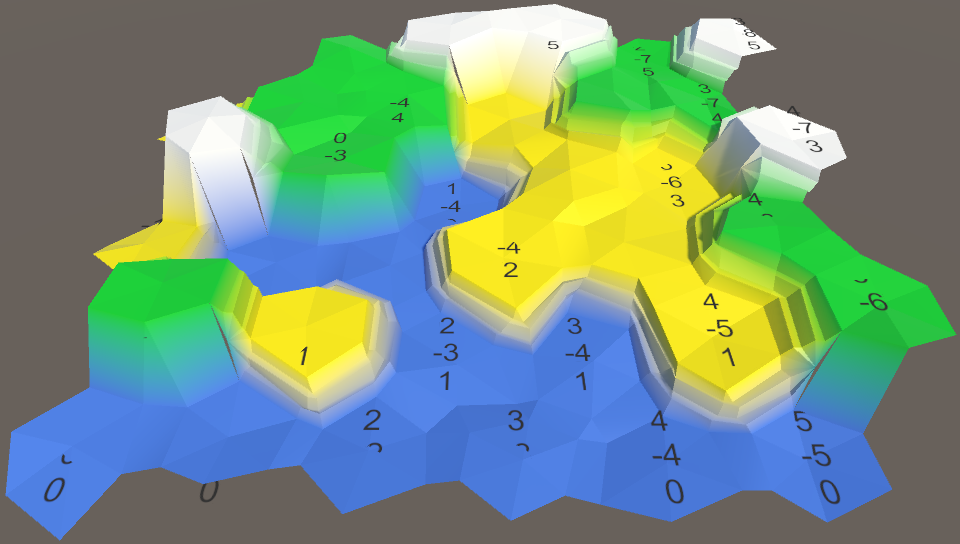
Карта стала менее строгой, но появилось больше проблем.
Проще всего решить проблему пересечений — сделать центры ячеек плоскими. Давайте просто не будем изменять координату Y в HexMesh.Perturb.
Vector3 Perturb (Vector3 position) {
Vector4 sample = HexMetrics.SampleNoise(position);
position.x += (sample.x * 2f - 1f) * HexMetrics.cellPerturbStrength;
// position.y += (sample.y * 2f - 1f) * HexMetrics.cellPerturbStrength;
position.z += (sample.z * 2f - 1f) * HexMetrics.cellPerturbStrength;
return position;
}
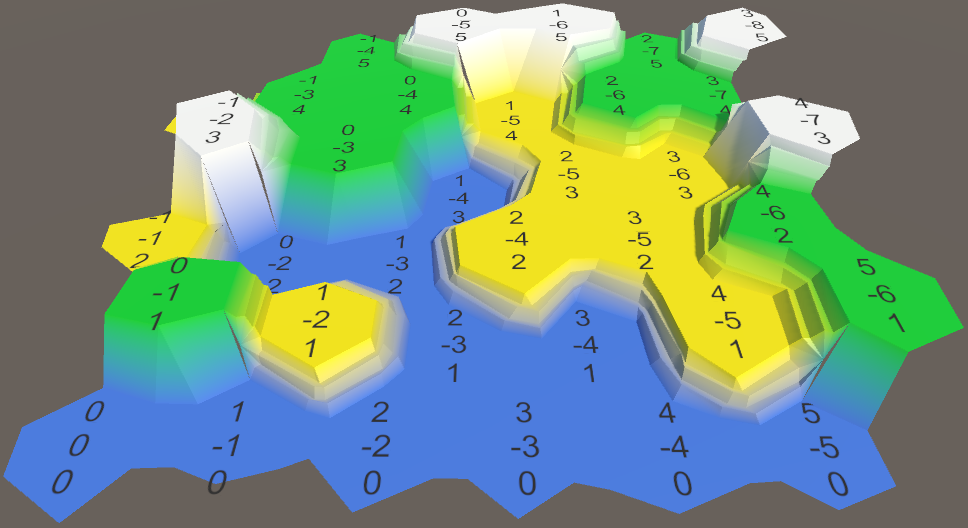
Выровненные ячейки.
При таком изменении все вертикальные позиции останутся неизменными, и у центров ячеек, и у ступенек уступов. Стоит учесть, что это снижает максимальное смещение до √50 ≈ 7.07 только в плоскости XZ.
Это неплохое изменение, потому что оно упрощает идентификацию отдельных ячеек и не позволяет уступам становиться слишком хаотичными. Но было бы всё равно неплохо добавить небольшое вертикальное перемещение.
Перемещение высоты ячейки
Вместо того, чтобы применять вертикальное перемещение к каждой вершине, мы можем применить его к ячейке. В этом случае каждая ячейка останется плоской, но между ячейками всё равно сохранится вариативность. Логично будет также использовать для перемещения высоты другой масштаб, поэтому добавим его в HexMetrics. Сила в 1.5 единиц создаёт небольшую вариативность, примерно равную высоте одной ступени уступа.
public const float elevationPerturbStrength = 1.5f;
Изменим свойство HexCell.Elevation так, чтобы оно применяло это перемещение к вертикальной позиции ячейки.
public int Elevation {
get {
return elevation;
}
set {
elevation = value;
Vector3 position = transform.localPosition;
position.y = value * HexMetrics.elevationStep;
position.y +=
(HexMetrics.SampleNoise(position).y * 2f - 1f) *
HexMetrics.elevationPerturbStrength;
transform.localPosition = position;
Vector3 uiPosition = uiRect.localPosition;
uiPosition.z = -position.y;
uiRect.localPosition = uiPosition;
}
}
Чтобы перемещение применялось сразу же, нам нужно явным образом задавать высоту каждой ячейки в HexGrid.CreateCell. В противном случае сетка изначально будет плоской. Сделаем это в конце, после создания UI.
void CreateCell (int x, int z, int i) {
…
cell.Elevation = 0;
}
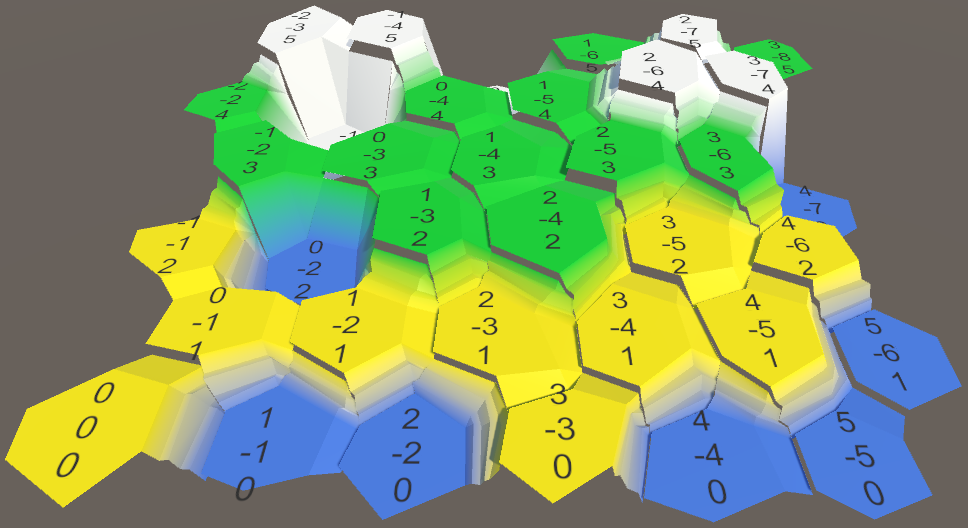
Перемещённые высоты с трещинами.
Использование одинаковых высот
В меше появилось множество трещин, потому что при триангуляции меша мы не используем одинаковые высоты ячеек. Давайте добавим в HexCell свойство для получения её позиции, чтобы можно было использовать её где угодно.
public Vector3 Position {
get {
return transform.localPosition;
}
}
Теперь мы можем использовать это свойство в HexMesh.Triangulate для определения центра ячейки.
void Triangulate (HexDirection direction, HexCell cell) {
Vector3 center = cell.Position;
…
}
И мы можем использовать его в TriangulateConnection при определении вертикальных позиций соседних ячеек.
void TriangulateConnection (
HexDirection direction, HexCell cell, Vector3 v1, Vector3 v2
) {
…
Vector3 bridge = HexMetrics.GetBridge(direction);
Vector3 v3 = v1 + bridge;
Vector3 v4 = v2 + bridge;
v3.y = v4.y = neighbor.Position.y;
…
HexCell nextNeighbor = cell.GetNeighbor(direction.Next());
if (direction <= HexDirection.E && nextNeighbor != null) {
Vector3 v5 = v2 + HexMetrics.GetBridge(direction.Next());
v5.y = nextNeighbor.Position.y;
…
}
}
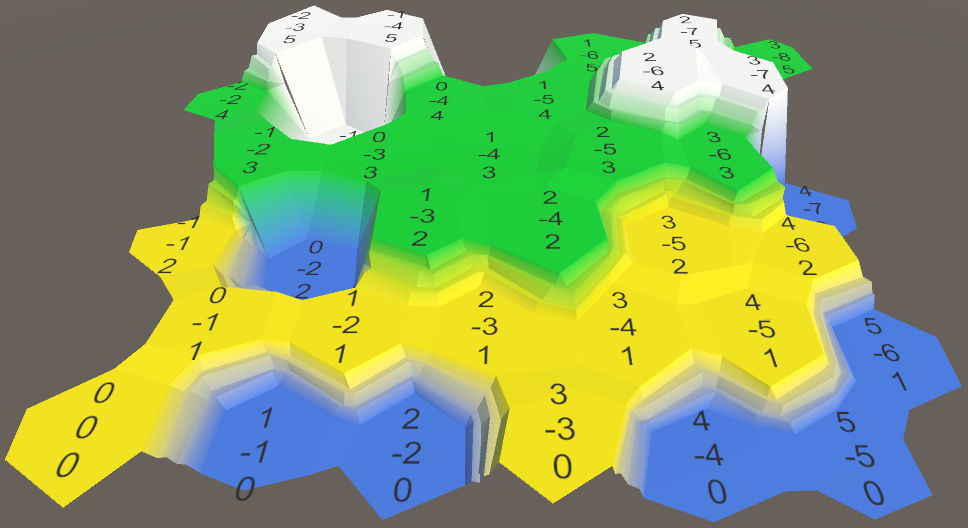
Согласованное использование высоты ячеек.
unitypackage
Подразделение рёбер ячеек
Хотя у ячеек и появилась красивая вариативность, они по-прежнему выглядят как очевидные шестиугольники. Само по себе это не проблема, но мы можем улучшить их внешний вид.
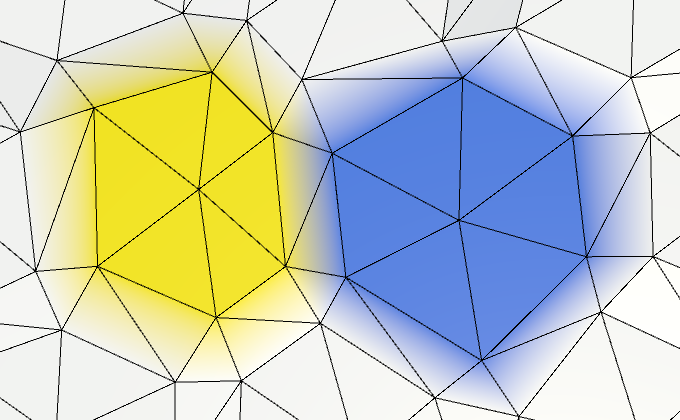
Чётко видимые шестиугольные ячейки.
Если бы у нас было больше вершин, то появилась бы бОльшая локальная вариативность. Так что давайте разобьём каждое ребро ячейки на две части, добавив вершину ребра посередине между каждой парой углов. Это значит, что HexMesh.Triangulate должен добавлять не один, а два треугольника.
void Triangulate (HexDirection direction, HexCell cell) {
Vector3 center = cell.Position;
Vector3 v1 = center + HexMetrics.GetFirstSolidCorner(direction);
Vector3 v2 = center + HexMetrics.GetSecondSolidCorner(direction);
Vector3 e1 = Vector3.Lerp(v1, v2, 0.5f);
AddTriangle(center, v1, e1);
AddTriangleColor(cell.color);
AddTriangle(center, e1, v2);
AddTriangleColor(cell.color);
if (direction <= HexDirection.SE) {
TriangulateConnection(direction, cell, v1, v2);
}
}
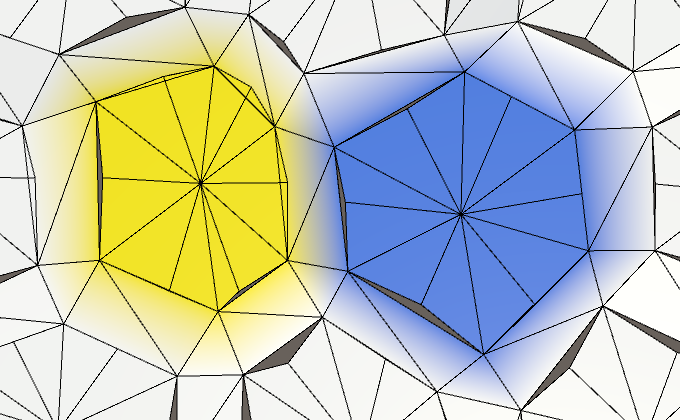
Двенадцать сторон вместо шести.
Удвоение вершин и треугольников добавляет рёбрам ячейки бОльшую вариативность. Давайте сделаем их ещё более неровными, утроив количество вершин.
Vector3 e1 = Vector3.Lerp(v1, v2, 1f / 3f);
Vector3 e2 = Vector3.Lerp(v1, v2, 2f / 3f);
AddTriangle(center, v1, e1);
AddTriangleColor(cell.color);
AddTriangle(center, e1, e2);
AddTriangleColor(cell.color);
AddTriangle(center, e2, v2);
AddTriangleColor(cell.color);
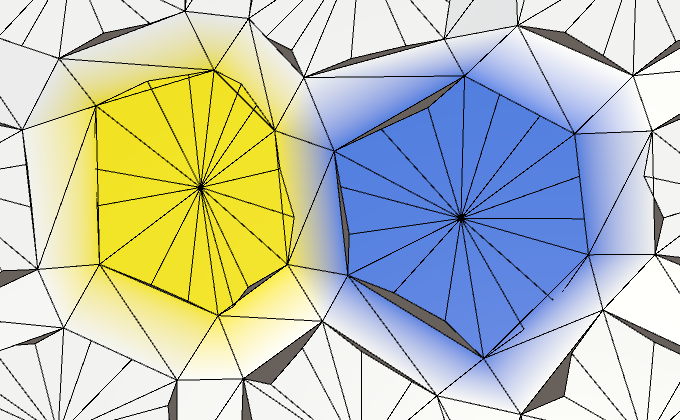
18 сторон.
Подразделение соединений рёбер
Разумеется, нам нужно также подразделить и соединения рёбер. Поэтому передадим новые вершины рёбер в TriangulateConnection.
if (direction <= HexDirection.SE) {
TriangulateConnection(direction, cell, v1, e1, e2, v2);
}
Добавим соответствующие параметры в TriangulateConnection, чтобы он мог работать с дополнительными вершинами.
void TriangulateConnection (
HexDirection direction, HexCell cell,
Vector3 v1, Vector3 e1, Vector3 e2, Vector3 v2
) {
…
}
Также нам нужно вычислить дополнительные вершины рёбер для соседних ячеек. Мы можем их вычислить после соединения мостом с другой стороной.
Vector3 bridge = HexMetrics.GetBridge(direction);
Vector3 v3 = v1 + bridge;
Vector3 v4 = v2 + bridge;
v3.y = v4.y = neighbor.Position.y;
Vector3 e3 = Vector3.Lerp(v3, v4, 1f / 3f);
Vector3 e4 = Vector3.Lerp(v3, v4, 2f / 3f);
Далее нам нужно изменить триангуляцию ребра. Пока мы проигнорируем склоны с уступами, просто добавим вместо одного quad три.
if (cell.GetEdgeType(direction) == HexEdgeType.Slope) {
TriangulateEdgeTerraces(v1, v2, cell, v3, v4, neighbor);
}
else {
AddQuad(v1, e1, v3, e3);
AddQuadColor(cell.color, neighbor.color);
AddQuad(e1, e2, e3, e4);
AddQuadColor(cell.color, neighbor.color);
AddQuad(e2, v2, e4, v4);
AddQuadColor(cell.color, neighbor.color);
}

Подразделённые соединения.
Объединение вершин рёбер
Так как для описания ребра нам теперь нужно четыре вершины, то логично будет объединить их в набор. Это удобнее, чем работать с четырьмя независимыми вершинами. Создадим для этого простую структуру EdgeVertices. Она должна содержать четыре вершины, идущие в порядке по часовой стрелке по ребру ячейки.
using UnityEngine;
public struct EdgeVertices {
public Vector3 v1, v2, v3, v4;
}
Мы будем использовать эту структуру только при триангуляции. На этом этапе нам не нужно хранить вершины рёбер, поэтому сериализуемыми их делать необязательно.
Добавим ей удобный метод-конструктор, который займётся вычислением промежуточных точек ребра.
public EdgeVertices (Vector3 corner1, Vector3 corner2) {
v1 = corner1;
v2 = Vector3.Lerp(corner1, corner2, 1f / 3f);
v3 = Vector3.Lerp(corner1, corner2, 2f / 3f);
v4 = corner2;
}
Теперь мы можем добавить в HexMesh отдельный метод триангуляции для создания веера треугольников между центром ячейки и одним из её рёбер.
void TriangulateEdgeFan (Vector3 center, EdgeVertices edge, Color color) {
AddTriangle(center, edge.v1, edge.v2);
AddTriangleColor(color);
AddTriangle(center, edge.v2, edge.v3);
AddTriangleColor(color);
AddTriangle(center, edge.v3, edge.v4);
AddTriangleColor(color);
}
И метод для триангуляции полосы четырёхугольников между двумя рёбрами.
void TriangulateEdgeStrip (
EdgeVertices e1, Color c1,
EdgeVertices e2, Color c2
) {
AddQuad(e1.v1, e1.v2, e2.v1, e2.v2);
AddQuadColor(c1, c2);
AddQuad(e1.v2, e1.v3, e2.v2, e2.v3);
AddQuadColor(c1, c2);
AddQuad(e1.v3, e1.v4, e2.v3, e2.v4);
AddQuadColor(c1, c2);
}
Это позволит нам упростить метод Triangulate.
void Triangulate (HexDirection direction, HexCell cell) {
Vector3 center = cell.Position;
EdgeVertices e = new EdgeVertices(
center + HexMetrics.GetFirstSolidCorner(direction),
center + HexMetrics.GetSecondSolidCorner(direction)
);
TriangulateEdgeFan(center, e, cell.color);
if (direction <= HexDirection.SE) {
TriangulateConnection(direction, cell, e);
}
}
Перейдём к TriangulateConnection. Теперь мы можем использовать TriangulateEdgeStrip, но нужно внести и другие замены. Там, где мы раньше использовали v1, нам нужно использовать e1.v1. Аналогично, v2 становится e1.v4, v3 становится e2.v1, а v4 становится e2.v4.
void TriangulateConnection (
HexDirection direction, HexCell cell, EdgeVertices e1
) {
HexCell neighbor = cell.GetNeighbor(direction);
if (neighbor == null) {
return;
}
Vector3 bridge = HexMetrics.GetBridge(direction);
bridge.y = neighbor.Position.y - cell.Position.y;
EdgeVertices e2 = new EdgeVertices(
e1.v1 + bridge,
e1.v4 + bridge
);
if (cell.GetEdgeType(direction) == HexEdgeType.Slope) {
TriangulateEdgeTerraces(e1.v1, e1.v4, cell, e2.v1, e2.v4, neighbor);
}
else {
TriangulateEdgeStrip(e1, cell.color, e2, neighbor.color);
}
HexCell nextNeighbor = cell.GetNeighbor(direction.Next());
if (direction <= HexDirection.E && nextNeighbor != null) {
Vector3 v5 = e1.v4 + HexMetrics.GetBridge(direction.Next());
v5.y = nextNeighbor.Position.y;
if (cell.Elevation <= neighbor.Elevation) {
if (cell.Elevation <= nextNeighbor.Elevation) {
TriangulateCorner(
e1.v4, cell, e2.v4, neighbor, v5, nextNeighbor
);
}
else {
TriangulateCorner(
v5, nextNeighbor, e1.v4, cell, e2.v4, neighbor
);
}
}
else if (neighbor.Elevation <= nextNeighbor.Elevation) {
TriangulateCorner(
e2.v4, neighbor, v5, nextNeighbor, e1.v4, cell
);
}
else {
TriangulateCorner(
v5, nextNeighbor, e1.v4, cell, e2.v4, neighbor
);
}
}
Подразделение уступов
Нам нужно подразделить и уступы. Поэтому передадим рёбра TriangulateEdgeTerraces.
if (cell.GetEdgeType(direction) == HexEdgeType.Slope) {
TriangulateEdgeTerraces(e1, cell, e2, neighbor);
}
Теперь мы должны изменить TriangulateEdgeTerraces так, чтобы он выполнял интерполяцию между рёбрами, а не между парами вершин. Давайте предположим, что у EdgeVertices есть для этого удобный статический метод. Это позволит нам упростить TriangulateEdgeTerraces, а не усложнять его.
void TriangulateEdgeTerraces (
EdgeVertices begin, HexCell beginCell,
EdgeVertices end, HexCell endCell
) {
EdgeVertices e2 = EdgeVertices.TerraceLerp(begin, end, 1);
Color c2 = HexMetrics.TerraceLerp(beginCell.color, endCell.color, 1);
TriangulateEdgeStrip(begin, beginCell.color, e2, c2);
for (int i = 2; i < HexMetrics.terraceSteps; i++) {
EdgeVertices e1 = e2;
Color c1 = c2;
e2 = EdgeVertices.TerraceLerp(begin, end, i);
c2 = HexMetrics.TerraceLerp(beginCell.color, endCell.color, i);
TriangulateEdgeStrip(e1, c1, e2, c2);
}
TriangulateEdgeStrip(e2, c2, end, endCell.color);
}
Метод EdgeVertices.TerraceLerp просто выполняет интерполяцию уступов между всеми четырьмя парами вершин двух рёбер.
public static EdgeVertices TerraceLerp (
EdgeVertices a, EdgeVertices b, int step)
{
EdgeVertices result;
result.v1 = HexMetrics.TerraceLerp(a.v1, b.v1, step);
result.v2 = HexMetrics.TerraceLerp(a.v2, b.v2, step);
result.v3 = HexMetrics.TerraceLerp(a.v3, b.v3, step);
result.v4 = HexMetrics.TerraceLerp(a.v4, b.v4, step);
return result;
}
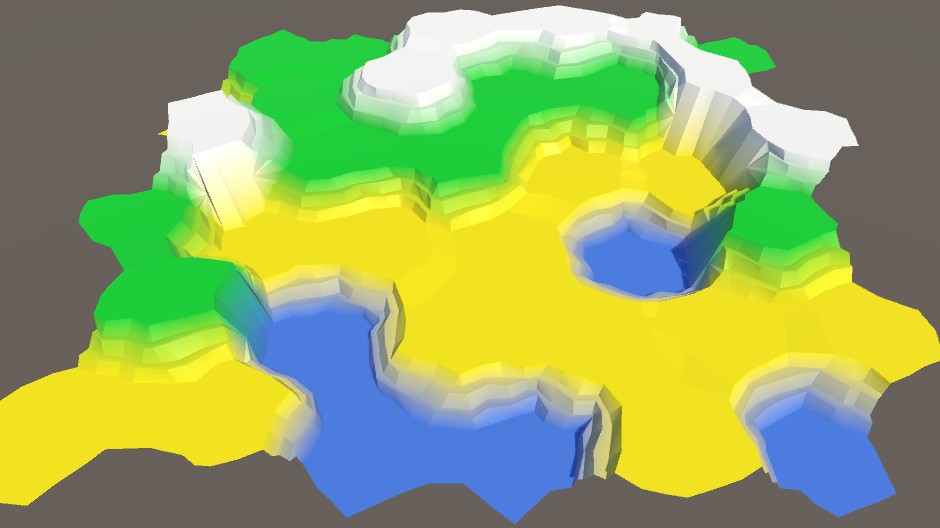
Подразделённые уступы.
unitypackage
Заново соединяем обрывы и уступы
Пока мы игнорировали трещины в местах соединений обрывов и уступов. Настало время решить эту проблему. Давайте сначала рассмотрим случаи «обрыв-склон-склон» (ОСС) и «склон-обрыв-склон» (СОС).
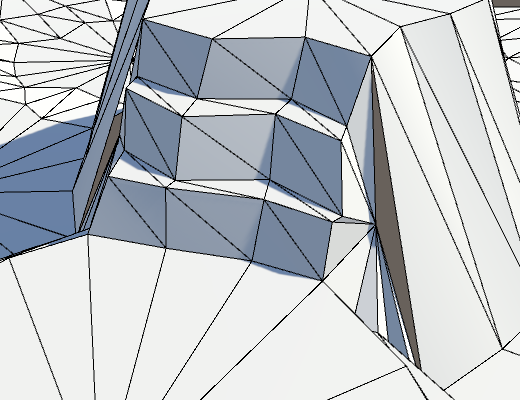
Дыры в меше.
Проблема возникает потому, что вершины границ переместились. Это означает, что теперь они не лежат ровно на боку обрыва, что приводит к трещине. Иногда эти дыры незаметны, а иногда бросаются в глаза.
Решение состоит в том, чтобы не перемещать вершину границы. Это значит, что нам нужно управлять тем, будет ли перемещена точка. Проще всего будет создать альтернативу AddTriangle, которая вообще не перемещает вершины.
void AddTriangleUnperturbed (Vector3 v1, Vector3 v2, Vector3 v3) {
int vertexIndex = vertices.Count;
vertices.Add(v1);
vertices.Add(v2);
vertices.Add(v3);
triangles.Add(vertexIndex);
triangles.Add(vertexIndex + 1);
triangles.Add(vertexIndex + 2);
}
Изменим TriangulateBoundaryTriangle так, чтобы он использовал этот метод. Это значит, что он должен будет явным образом перемещать все вершины, за исключением граничных.
void TriangulateBoundaryTriangle (
Vector3 begin, HexCell beginCell,
Vector3 left, HexCell leftCell,
Vector3 boundary, Color boundaryColor
) {
Vector3 v2 = HexMetrics.TerraceLerp(begin, left, 1);
Color c2 = HexMetrics.TerraceLerp(beginCell.color, leftCell.color, 1);
AddTriangleUnperturbed(Perturb(begin), Perturb(v2), boundary);
AddTriangleColor(beginCell.color, c2, boundaryColor);
for (int i = 2; i < HexMetrics.terraceSteps; i++) {
Vector3 v1 = v2;
Color c1 = c2;
v2 = HexMetrics.TerraceLerp(begin, left, i);
c2 = HexMetrics.TerraceLerp(beginCell.color, leftCell.color, i);
AddTriangleUnperturbed(Perturb(v1), Perturb(v2), boundary);
AddTriangleColor(c1, c2, boundaryColor);
}
AddTriangleUnperturbed(Perturb(v2), Perturb(left), boundary);
AddTriangleColor(c2, leftCell.color, boundaryColor);
}
Стоит заметить следующее: поскольку мы не используем v2 для получения какой-то другой точки, то можно переместить её сразу же. Это простая оптимизация и она уменьшает объём кода, так что давайте внесём её.
void TriangulateBoundaryTriangle (
Vector3 begin, HexCell beginCell,
Vector3 left, HexCell leftCell,
Vector3 boundary, Color boundaryColor
) {
Vector3 v2 = Perturb(HexMetrics.TerraceLerp(begin, left, 1));
Color c2 = HexMetrics.TerraceLerp(beginCell.color, leftCell.color, 1);
AddTriangleUnperturbed(Perturb(begin), v2, boundary);
AddTriangleColor(beginCell.color, c2, boundaryColor);
for (int i = 2; i < HexMetrics.terraceSteps; i++) {
Vector3 v1 = v2;
Color c1 = c2;
v2 = Perturb(HexMetrics.TerraceLerp(begin, left, i));
c2 = HexMetrics.TerraceLerp(beginCell.color, leftCell.color, i);
AddTriangleUnperturbed(v1, v2, boundary);
AddTriangleColor(c1, c2, boundaryColor);
}
AddTriangleUnperturbed(v2, Perturb(left), boundary);
AddTriangleColor(c2, leftCell.color, boundaryColor);
}

Неперемещённые границы.
Так выглядит лучше, но мы ещё не закончили. Внутри метода TriangulateCornerTerracesCliff граничная точка находится интерполяцией между левой и правой точками. Однако эти точки ещё не перемещены. Чтобы граничная точка соответствовала получающемуся обрыву, нам нужно выполнять интерполяцию между перемещёнными точками.
Vector3 boundary = Vector3.Lerp(Perturb(begin), Perturb(right), b);
То же самое справедливо для метода TriangulateCornerCliffTerraces.
Vector3 boundary = Vector3.Lerp(Perturb(begin), Perturb(left), b);

Дыры пропали.
Двойные обрывы и склон
Во всех оставшихся проблемных случаях присутствуют два обрыва и один склон.

Большая дыра из-за единственного треугольника.
Эта проблема устраняется с помощью ручного перемещения единственного треугольника в блоке else в конце TriangulateCornerTerracesCliff.
else {
AddTriangleUnperturbed(Perturb(left), Perturb(right), boundary);
AddTriangleColor(leftCell.color, rightCell.color, boundaryColor);
}
То же самое относится и к TriangulateCornerCliffTerraces.
else {
AddTriangleUnperturbed(Perturb(left), Perturb(right), boundary);
AddTriangleColor(leftCell.color, rightCell.color, boundaryColor);
}
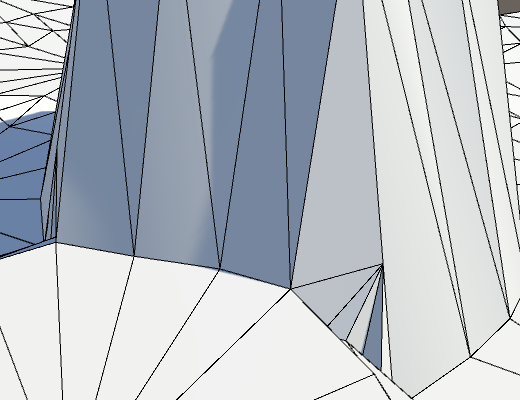
Избавились от последних трещин.
unitypackage
Доработка
Теперь у нас есть полностью корректный искажённый меш. Его внешний вид зависит от конкретного шума, его масштаба и сил искажения. В нашем случае искажение может показаться слишком сильным. Хотя такая неравномерность выглядит красиво, мы не хотим, чтобы ячейки слишком отклонялись от ровной сетки. В конце концов, мы по-прежнему используем её для того, чтобы определить изменяемую ячейку. И если размер ячеек будет слишком сильно варьироваться, то нам сложнее будет разместить в них содержимое.
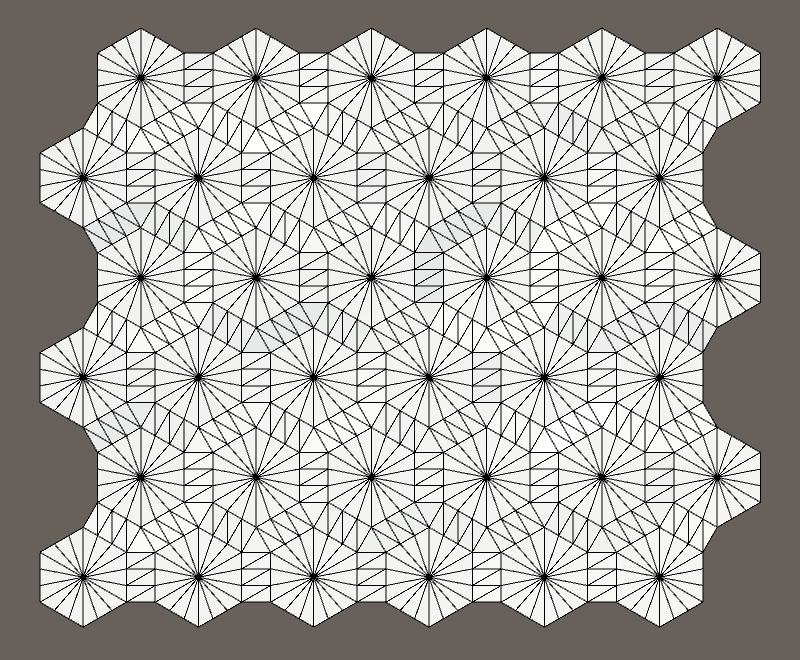
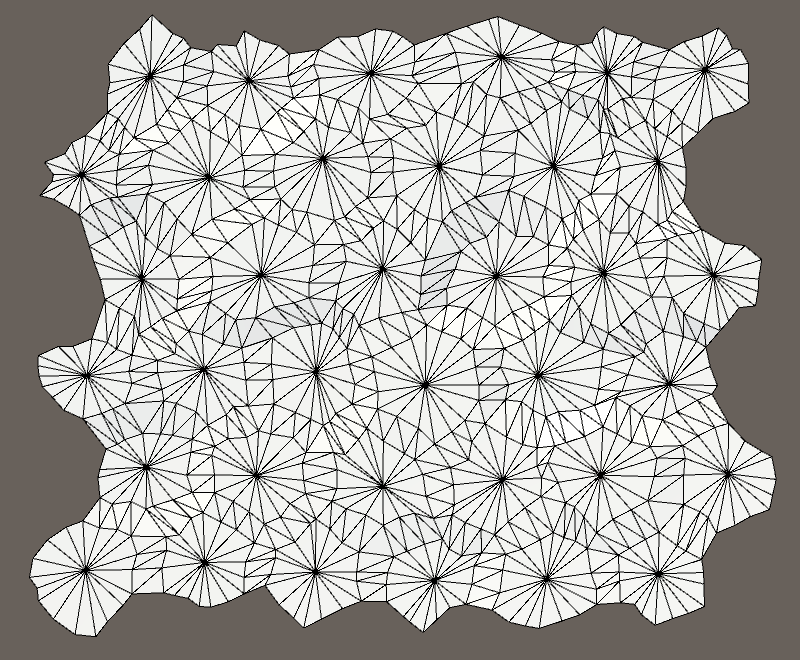
Неискажённая и искажённая сетки.
Похоже, что сила 5 для искажения ячеек слишком велика.
Искажение ячеек от 0 до 5.
Давайте уменьшим её до 4, чтобы повысить удобство сетки, не делая при этом её слишком правильной. Это гарантирует нам, что максимальное смещение по XZ будет равно √32 ≈ 5.66 единицам.
public const float cellPerturbStrength = 4f;
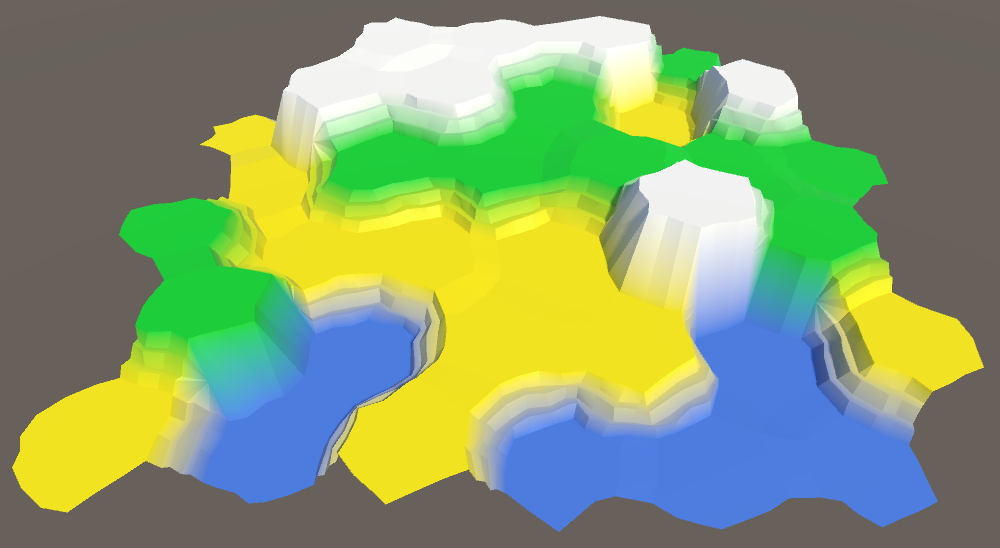
Сила искажения ячеек 4.
Ещё одно значение, которое можно изменять — это коэффициент цельности. Если мы увеличим его, то плоские центры ячеек станут больше, то есть появится больше места для будущего содержимого. Разумеется, при этом они станут более шестиугольными.
Коэффициент цельности от 0.75 до 0.95.
Небольшое увеличение коэффициента цельности до 0.8 немного упростит нашу жизнь в будущем.
public const float solidFactor = 0.8f;
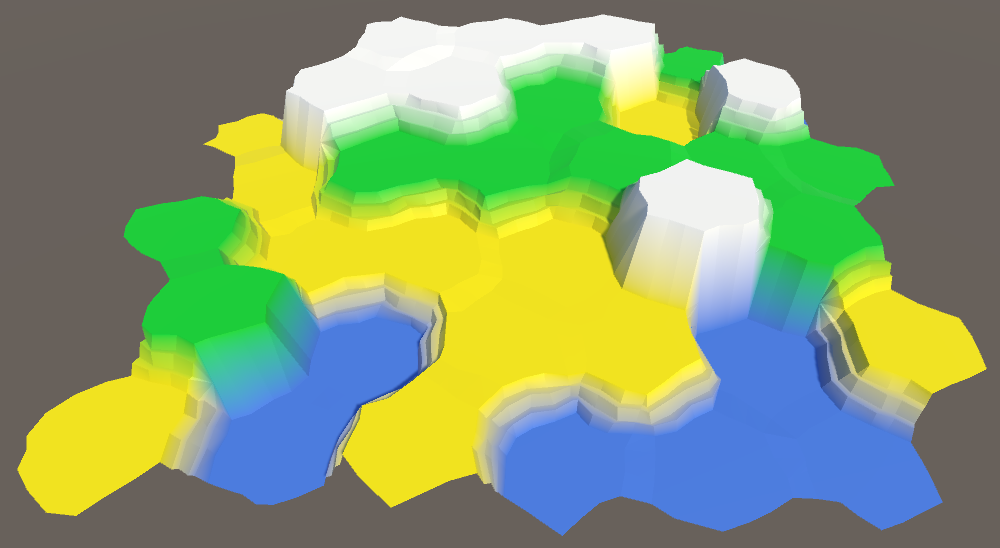
Коэффициент цельности 0.8.
Наконец, можно заметить, что разницы между уровнями высот слишком резкие. Это удобно, когда нужно убедиться в правильной генерации меша, но мы с этим уже закончили. Давайте уменьшим её до 1 единицы на ступень уступа, то есть до 3.
public const float elevationStep = 3f;

Шаг высоты уменьшен до 3.
Также мы можем изменить силу искажения высоты. Но сейчас она имеет значение 1.5, что равно половине шага высоты, что нас устроит.
Небольшие шаги высот позволяют логичнее использовать все семь уровней высоты. Благодаря этому повышается вариативность карты.

Используем семь уровней высот.
unitypackage
- Разделяем сетку на фрагменты.
- Управляем камерой.
- Раскрашиваем цвета и высоты по отдельности.
- Используем увеличенную кисть ячеек.
Пока что мы работали с очень маленькой картой. Настало время её увеличить.

Пришла пора увеличить масштаб.
Фрагменты сетки
Мы не можем сделать сетку слишком большой, потому что упрёмся в пределы того, что можно уместить в один меш. Как же решить эту проблему? Использовать несколько мешей. Для этого надо разделить нашу сетку на несколько фрагментов. Мы используем прямоугольные фрагменты постоянного размера.
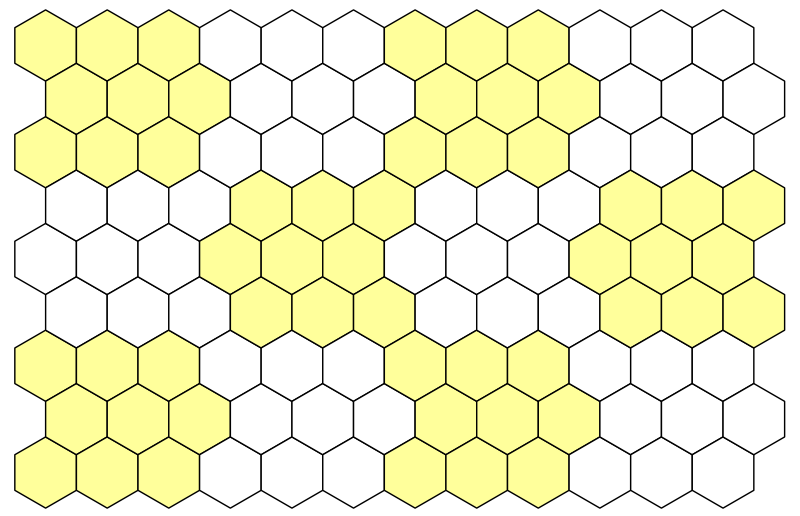
Разбиение сетки на сегменты 3 на 3.
Давайте используем блоки 5 на 5, то есть по 25 ячеек на фрагмент. Определим их в HexMetrics.
public const int chunkSizeX = 5, chunkSizeZ = 5;
Сложно сказать. При использовании больших фрагментов мешей нужно меньше, но их размер будет больше. При этом снижается количество вызовов отрисовки. Но чем меньше фрагменты по размерам, тем лучше они отсекаются пирамидой видимости (frustum culling), что приводит к отрисовке меньшего количества треугольников. Логичнее будет просто выбрать размер и при необходимости подстроить его в дальнейшем.
Теперь мы не можем использовать для сетки любой размер, он должен быть кратным размеру фрагмента. Поэтому давайте изменим HexGrid так, чтобы он задавал её размер не в отдельных ячейках, а во фрагментах. Зададим по умолчанию размер 4 на 3 фрагментов, то есть всего 12 фрагментов или 300 ячеек. Так мы получим удобную тестовую карту.
public int chunkCountX = 4, chunkCountZ = 3;
Мы по-прежнему пользуемся width и height, но теперь они должны стать частными. И переименуем их в cellCountX и cellCountZ. Воспользуйтесь редактором, чтобы переименовать все вхождения этих переменных за один раз. Теперь будет понятно, когда мы имеем дело с количеством фрагментов или ячеек.
// public int width = 6;
// public int height = 6;
int cellCountX, cellCountZ;
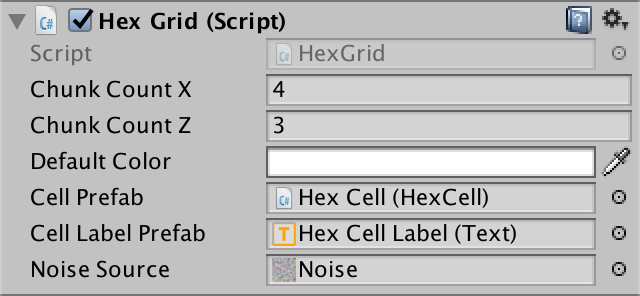
Указываем размер во фрагментах.
Изменим Awake так, чтобы при необходимости из количества фрагментов вычислялось количество ячеек. Выделим создание ячеек в отдельный метод, чтобы не засорять Awake.
void Awake () {
HexMetrics.noiseSource = noiseSource;
gridCanvas = GetComponentInChildren
Префаб фрагмента
Для описания фрагментов сетки нам понадобится новый тип компонентов.
using U
