[Перевод] Как работают ленивые вычисления
Маленькая Лямбда решила, что уборку в комнате можно отложить и на потом.Ленивые вычисления — часто используемая методика при исполнении компьютером программ на Haskell. Они делают наш код проще и модульнее, но могут вызвать и замешательство, особенно когда речь заходит об использовании памяти, становясь для новичков распространённой ловушкой. Например, безобидно выглядящее выражение
foldl (+) 0 [1…10^8] потребует для своего вычисления гигабайты памяти.В этом руководстве я хочу объяснить, как работают ленивые вычисления и что они означают для времени выполнения и объёма памяти, затрачиваемыми программами на Haskell. Я начну рассказ с основ редукции графов, а после перейду к обсуждению строгой левой свёртки — простейшего примера для понимания и ликвидации утечек памяти.
Тема ленивых вычислений рассматривалась во многих учебниках (например, в книге Саймона Томпсона «Haskell — The Craft of Functional Programming»), но информацию о них, кажется, всё ещё проблематично найти в сети. Надеюсь, моё руководство посодействует решению этой проблемы.
Ленивые вычисления — это компромисс. С одной стороны, они помогают нам сделать код более модульным. С другой стороны, бывает невозможно до конца разобраться, как происходит вычисление в конкретной программе — всегда существуют небольшие отличия между реальностью и тем, что вы о ней думаете. В конце статьи я дам рекомендации, как поступать в ситуациях такого рода. Итак, приступим!
Основы: редукция графовВыражения, графы и редексы
Выполнение программ на Haskell означает вычисление выражений. Основная идея, скрывающаяся за этим, называется применением функции. Пусть дана функция
square x = x*x
Мы можем вычислить выражение
square (1+2),
заменяя square в левой части определения его правой частью до тех пор, пока не получим значение переменной x для текущего аргумента.
square (1+2)
=> (1+2)*(1+2)
Здесь используются две функции: + и *
(1+2)*(1+2)
=> 3*(1+2)
=> 3×3
=> 9
Обратите внимание, что в этом случае нам приходится дважды вычислять (1+2). Однако, понятно, что на самом деле ответы одинаковы, поскольку оба выражения связаны с одним и тем же аргументом x.Чтобы избежать ненужного дублирования, мы используем метод под названием «редукция графов». Вообще говоря, любое выражение может быть представлено в виде графа. Для нашего примера это выглядит следующим образом: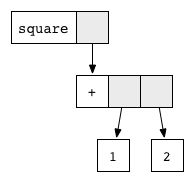 
Каждый блок соотносится с применением соответствующей функции, чьё имя написано на белом поле, а серые поля указывают на аргументы. Эта графическая нотация похожа на то, как компилятор на самом деле представляет выражение с указателями на ячейки памяти.
Каждая функция, определённая программистом, соответствует редукционному правилу. Например, правило для square выглядит следующим образом: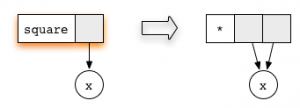 
Обведённый кружком x замещает собой подграф. Обратите внимание: оба аргумента функции умножения указывают на один подграф. Такой способ общего его использования — ключ к отсутствию дублирования.
Любой подграф, соответствующий правилу, называется сокращаемым выражением (reducible expression) или редексом (redex) для краткости. Где бы мы не встретили редекс, мы можем сократить его, чем обновим соответствующий правилу выделенный прямоугольник. В нашем примере есть два редекса: можно сократить либо функцию square, либо сложение (+).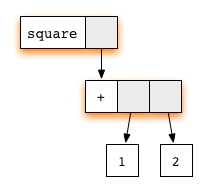
Если мы начнём с редекса square, а затем продолжим вычисление с редексом сложения, то получим цепочку
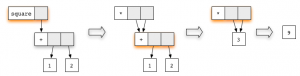На каждом шаге редекс, выделенный цветом, обновляется. На предпоследнем графе появляется новый редекс, связанный с правилом умножения. Выполнив эту редукцию, мы получим итоговый результат 9.
Нормальная форма и слабая заголовочная нормальная форма
Если выражение (граф) не содержит редексов, т.е. в нём ничего нельзя сократить, то дело сделано. Когда так происходит, мы говорим, что выражение находится в нормальной форме. Это итоговый результат вычисления. В предыдущем примере нормальной формой было единственное число, представленное графом
Но конструкторы наподобие Just, Nothing или конструкторов списков : и [] также сводятся к нормальной форме. При этом они выглядят, как функции, но поскольку представлены декларацией data и не имеют правой части, то правило редукции для них отсутствует. Например, граф
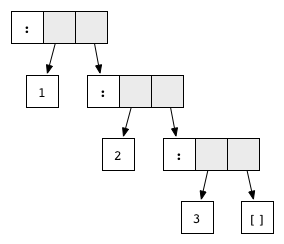нормальная форма списка 1:2:3:[].Вообще говоря, есть ещё два требования к графу, чтобы его можно было называть находящимся в нормальной форме. Во-первых, он должен быть конечным, а во-вторых, не иметь циклов. Противоположное этим условиям иногда встречается при рекурсии. Например, выражение, определённое как
ones = 1: ones
соотносится с цикличным графом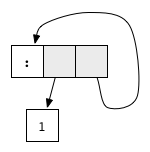
Он не имеет редексов, но и не находится в нормальной форме: хвост списка рекурсивно указывает на сам список, в результате порождая бесконечный цикл.В Haskell мы обычно не выводим нормальную форму полностью. Более того, чаще всего мы останавливаемся, когда граф достигает слабой заголовочной нормальной формы (weak head normal form, WHNF). Говорят, что граф находится в WHNF, если самый верхний его узел является конструктором. Например, выражение (7+12):[] или
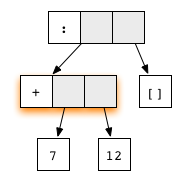находится в WHNF, поскольку его верхний узел — конструктор списка (:). И это не нормальная форма, так как первый аргумент содержит редекс.
С другой стороны, любой граф, не находящийся в WHNF, называется не вычисленным выражением или преобразователем. Выражение, которое начинается с конструктора, находится в WHNF, но его аргументы запросто могут быть не вычисленными.
Очень интересным примером графа в WHNF является граф функции ones, упомянутой выше. В конце-концов, самый верхний его элемент — конструктор. В Haskell мы можем создавать и манипулировать бесконечными списками! Они прекрасно подходят для того, чтобы код был более модульным.
Порядок вычислений, ленивые вычисления Часто выражение содержит несколько редексов. Насколько принципиальна последовательность, в которой мы будем сокращать их? Один из порядков редукции, называемый энергичным вычислением, вычисляет аргументы функции до их нормальной формы прежде, чем редуцировать её саму. Эта стратегия используется в большинстве языков программирования.
Однако, компиляторы Haskell обычно используют другой порядок вычислений, называемый ленивым, когда прежде всего редуцируется самое верхнее применение функции. При этом может возникнуть необходимость вычислить некоторые аргументы, но только в требуемом количестве. Рассмотрим функцию, определённую несколькими уравнениями с использованием сопоставления с образцом. Для каждого из них аргументы будут вычисляться слева направо до тех пор, пока их верхний узел не станет содержать конструктор, соответствующий образцу. Если сравнение происходит с обычной переменной, то аргументы не вычисляются. Если же образцом является конструктор, то это означает вычисление до WHNF.
Надеюсь, пример сделает эту концепцию понятнее. Пусть дана функция (&&), реализующая логическое И. Её определение выглядит следующим образом:
(&&) :: Bool → Bool → Bool
True && x = x
False && x = False
Оно представлено двумя правилами редукции, зависящими от значения первого аргумента: True или False.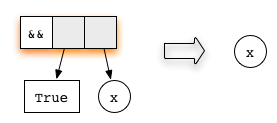
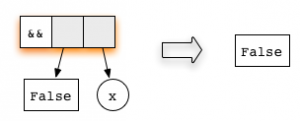Теперь рассмотрим выражение
('H' == 'i') && ('a' == 'm')
представляемое как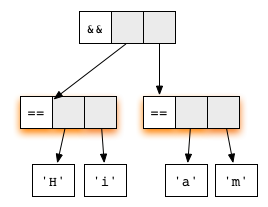
Оба аргумента в нём — редексы. Первое уравнение функции (&&) проверяет, соответствует ли первый аргумент конструктору True. Таким образом, ленивое вычисление начинается с редуцирования первого аргумента: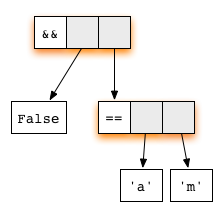 
Второй аргумент не вычисляется, поскольку самое верхнее применение функции уже является редексом. Ленивое вычисление всегда начинает редуцирование с самого верхнего узла, что мы и сделаем, используя правило для функции (&&). Получим
Это выражение находится в нормальной форме — следовательно, всё готово!
Обратите внимание, что если редуцировать применение (&&) так быстро, как только возможно, то искать значение второго аргумента никогда и не понадобится, что сократит общие затраты времени. Некоторые императивные языки используют похожий трюк, называемый «накоротко замкнутое вычисление». Однако, обычно этот функционал «вшит» в язык и работает только для логических операций. В Haskell такой метод может применяться ко всем функциям — это всего лишь последовательность ленивых вычислений.
В общем случае нормальная форма, полученная с помощью ленивых вычислений, никогда не отличается от результата выполнения того же самого выражения их энергичным коллегой. Так что в этом смысле не важно, в каком порядке происходит редукция. Однако, ленивые вычисления выполняются за меньшее количество шагов и могут иметь дело с цикличными (бесконечными) графами, что недоступно энергичным вычислениям.
Текстовое представление Надеюсь, визуальное представление выражений в виде графов помогло вам получить общее понятие о ленивых вычислениях, поскольку оно наглядно подчёркивает концепцию редекса и необходимый порядок редукции. Тем не менее, для конкретных расчётов рисование картинок несколько обременительно. Для отслеживания процесса редукции мы обычно работаем с текстовым представлением с использованием синтаксиса Haskell.Графы помогают легче визуализировать общие подграфы. В текстовом представлении нам нужно обозначать общие выражения, давая им имена с использованием ключевого слова let. Например, наш самый первый пример редуцирования выражения square (1+2) будет выглядеть так:
square (1+2) => let x = (1+2) in x*x => let x = 3 in x*x => 9 Синтаксис let… in позволяет сделать общим выражение x = (1+2). Обратите внимание, что ленивое вычисление сначала редуцирует функцию square, а только потом вычисляет аргумент x.Наш второй пример — логическое И — превращается в
('H' == 'i') && ('a' == 'm') => False && ('a' == 'm') => False В этом случае нет необходимости делать общим какое-либо подвыражение, так что ключевое слово let в коде отсутствует.С этого момента мы будем использовать только текстовое представление.
Время & память Рассмотрим теперь, что означают ленивые вычисления для времени работы и требуемого объёма памяти программ на Haskell. Если до сих пор вы имели дело только с энергичными вычислениями, то приготовьтесь к сюрпризам (особенно, когда речь пойдёт о памяти).Время Сколько шагов занимает вычисление выражения? Для энергичных вычислений ответ прост: у каждого применения функции мы складываем время, необходимое для вычисления её аргументов, с временем, требуемым на выполнение самого тела функции. Но что на счёт ленивых вычислений? К счастью, ситуация здесь благоприятная. Мы имеем следующий верхний предел: Теорема: ленивые вычисления никогда не совершают больше вычислительных шагов, чем энергичные вычисления.
Это означает, что в процессе анализа времени выполнения алгоритма мы всегда можем сделать вид, будто аргументы вычисляются «энергично». Например, можно транслитерировать код сортировочного алгоритма в Haskell и быть уверенными, что результат будет иметь ту же самую (а иногда и лучшую) алгоритмическую сложность, что и его энергичный двойник.
Тем не менее, реализация ленивых вычислений требует определённых административных расходов. Для приложений с высокой производительностью, наподобие обработки изображений или цифровых симуляций, выгодно «не лениться» и оставаться ближе к «железу». В противном случае, мантра «простой и модульный код» приводит нас к ленивым вычислениям. Например, оптимизация компилятора под названием «слияние потоков» имеет целью повышение производительности операций с массивами, как с модульным, спископодобным интерфейсом. Эта идея воплощена в библиотеке vector .
Память К несчастью, ситуация с использованием памяти не так проста, как со временем. Суть проблемы заключается в том, что объём памяти, требуемый не вычисленному выражению, может значительно отличаться от объёма, занимаемого его нормальной формой. Выражение использует тем больше места, чем больше узлов содержит граф. Например, ((((0 + 1) + 2) + 3) + 4) займёт под хранение больше памяти, чем его нормальная форма 10. Контрпримером может служить выражение enumFromTo 1 1000 чей более знакомый синтаксис выглядит как [1…1000]. Это применение функции состоит всего из трёх узлов, отчего занимает значительно меньше памяти, чем список 1:2:3: …:1000:[], содержащий как минимум тысячу элементов.Когда вариант с не вычисленным выражением выходит из-под контроля, происходит утечка памяти. Решением здесь станет контроль всего процесса вычисления, чтобы гарантировать его завершение как можно быстрее. Для этой цели в Haskell есть комбинатор
seq: a → b → b Как предполагает объявление типов, по существу он просто возвращает свой второй аргумент и ведёт себя в большей степени, как функция const. Однако, у выражения seq x y сначала до WHNF вычислится y, а только потом x. Наоборот, при вычислении const x y мы оставляем y в покое и немедленно вычисляем x.Рассмотрим прототипичный пример, показывающий, как использовать seq, и который должен знать каждый программист на Haskell: строгую левую свёртку. Пусть дано задание просуммировать все числа от 1 до 100. Мы будем это делать, используя аккумулирующий параметр, т.е. как в левой свёртке
foldl (+) 0 [1…100] Для справки: функция foldl определена в Haskell Prelude как foldl: (a → b → a) → a → [b] → a foldl f a [] = a foldl f a (x: xs) = foldl f (f a x) xs Процесс вычисления выглядит следующим образом: foldl (+) 0 [1…100] => foldl (+) 0 (1:[2…100]) => foldl (+) (0 + 1) [2…100] => foldl (+) (0 + 1) (2:[3…100]) => foldl (+) ((0 + 1) + 2) [3…100] => foldl (+) ((0 + 1) + 2) (3:[4…100]) => foldl (+) (((0 + 1) + 2) + 3) [4…100] =>… Как вы можете видеть, аккумулирующий параметр растёт от ветви к ветви — происходит утечка памяти. Чтобы её избежать, потребуется гарантия постоянного нахождения аккумулятора в WHNF. Следующая версия foldl проделывает этот трюк: foldl' :: (a → b → a) → a → [b] → a foldl' f a [] = a foldl' f a (x: xs) = let a' = f a x in seq a' (foldl' f a' xs) Её можно найти в модуле Data.List. Теперь процесс вычисления выглядит так: foldl' (+) 0 [1…100] => foldl' (+) 0 (1:[2…100]) => let a' = 0 + 1 in seq a' (foldl' (+) a' [2…100]) => let a' = 1 in seq a' (foldl' (+) a' [2…100]) => foldl' (+) 1 [2…100] => foldl' (+) 1 (2:[3…100]) => let a' = 1 + 2 in seq a' (foldl' (+) a' [3…100]) => let a' = 3 in seq a' (foldl' (+) a' [3…100]) => foldl' (+) 3 [3…100] =>… Во время вычисления выражение имеет постоянный размер. Использование seq гарантирует выведение WHNF аккумулирующего параметра до того, как будет рассмотрен следующий элемент списка.Как правило, функция foldl склонна к утечкам памяти, так что лучше использовать вместо неё foldl' или foldr.
Кстати, обратите внимание, что на языке с энергичными вычислениями для задачи суммировать цифры от 1 до 100 вы никогда не сможете написать код, подобный приведённому выше. В самом деле, в этом случае сначала вычислится до нормальной формы список [1…100], что займёт столько же места в памяти, сколько требуется неэффективной версии foldl. Если требуется решить задачу эффективно, то надо писать рекурсивный цикл. Но в Haskell ленивые вычисления позволяют это сделать одним применением комбинатора общего назначения для списка [1…100], который вычисляется «по требованию». Это ещё один пример того, как можно сделать код более модульным.
Другой важный урок, который можно извлечь из рассмотренной задачи, следующий: на самом деле вычисление, которое я показал, происходит не совсем так. Если мы определим список перечисления [n…m] как
enumFromTo n m = if n < m then n : enumFromTo (n+1) m else [] то редукция в WHNF на самом деле будет выглядеть так: [1..100] => 1: [(1+1)…100] т.е. новый первый аргумент не 2, а не вычисленное выражение (1+1). Не то чтобы здесь была большая разница, но имейте ввиду: вы должны быть очень осторожны при точной трассировке ленивых вычислений — они никогда не делают в точности так, как вы себе это представляете. Настоящий код для enumFromTo несколько отличается от показанного выше. В частности, обратите внимание, что [1…] строится, как список чисел, которые не находятся в WHNF.В принципе, я так долго об этом рассказывал, чтобы подвести к простому выводу: с ленивыми вычислениями не представляется возможным детально отследить трассировку, кроме совсем уж простых примеров. Таким образом, анализ использования памяти программами на Haskell — задача не из тривиальных. Мой совет: предпринимайте что-либо только в тех случаях, когда имеет место явная утечка памяти. Для этого я рекомендовал бы воспользоваться профилирующими инструментами, позволяющими разобраться в том, что же происходит. После того, как проблема сформулирована, инструменты вроде инвариантов пространства и seq могут гарантировать вычисление соответствующих выражений в WHNF, независимо от мелких деталей выполнения ленивых вычислений.
Вот и всё, что я хотел рассказать о ленивых вычислениях и использовании памяти. Есть ещё один важный пример утечки, который я не затронул, но который не менее хрестоматиен:
let small' = fst (small, large) in… small' … Выражение small' сохраняет ссылку на выражение large даже когда оно отбрасывается функцией fst. Возможно, вам стоит каким-то образом вычислять выражение small' в WHNF, чтобы можно было без проблем использовать память, занятую large.
