[Перевод] Как работает реляционная БД15.09.2015 14:18

Реляционные базы данных (РБД) используются повсюду. Они бывают самых разных видов, от маленьких и полезных SQLite до мощных Teradata. Но в то же время существует очень немного статей, объясняющих принцип действия и устройство реляционных баз данных. Да и те, что есть, довольно поверхностные, без особых подробностей. Зато по более «модным» направлениям (большие данные, NoSQL или JS) написано гораздо больше статей, причём куда более глубоких. Вероятно, такая ситуация сложилась из-за того, что реляционные БД — вещь «старая» и слишком скучная, чтобы разбирать её вне университетских программ, исследовательских работ и книг.

На самом деле, мало кто действительно понимает, как работают реляционные БД. А многие разработчики очень не любят, когда они чего-то не понимают. Если реляционные БД используют порядка 40 лет, значит тому есть причина. РБД — штука очень интересная, поскольку в ее основе лежат полезные и широко используемые понятия. Если вы хотели бы разобраться в том, как работают РБД, то эта статья для вас.
Сразу нужно подчеркнуть: из этого материала вы НЕ узнаете, как можно использовать БД. Однако для усвоения материала вы должны уметь написать хотя бы простенький запрос на соединение и CRUD-запрос. Этого вполне достаточно для понимания статьи, остальное будет объяснено.

Статья состоит из трёх частей:

Обзор низкоуровневых и высокоуровневых компонентов БД.
Обзор процесса оптимизации запросов.
Обзор управления транзакциями и буферным пулом.

Давным-давно (в далёкой-далёкой галактике) разработчики должны были держать в голове точное количество операций, которые они кодят. Они всем сердцем чувствовали алгоритмы структуры данных, поскольку не могли себе позволить тратить впустую ресурсы процессора и памяти на своих медленных компьютерах прошлого. В этой главе мы вспомним некоторые концепции, которые необходимы для понимания работы БД.

1.1. О (1) против О (n2)

Сегодня многие разработчики не особо задумываются о временнόй сложности алгоритмов… и они правы! Но когда приходится работать с большим объёмом данных, или если нужно экономить миллисекунды, то временнáя сложность становится крайне важна.

1.1.1. Концепция

Временнáя сложность используется для оценки производительности алгоритма, как долго будет выполняться алгоритм для входных данных определённого размера. Обозначается временнáя сложность как «О» (читается как «О большое»). Это обозначение используется вместе с функцией, описывающей количество операций, осуществляемых алгоритмом для обработки входных данных.

Например, если сказать «этот алгоритм есть О большое от некоторой функции», то это означает, что для определённого объёма входных данных алгоритму нужно выполнить количество операций, пропорциональное значению функции от этого определённого объёма данных.

Здесь важен не объём данных, а динамика увеличения количества операций с ростом объёма. Временнáя сложность не позволяет вычислить точное количество, но зато представляет собой хороший способ оценки.

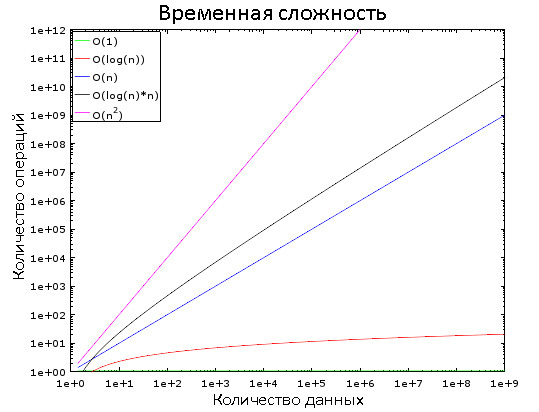
На этом графике вы видите, как изменяются разные классы сложностей. Для наглядности используется логарифмическая шкала. Иными словами, количество данных быстро увеличивается от 1 до 1 000 000. Мы видим, что:

O (1) является «константным временем», то есть её значение постоянно.
O (log (n)) — логарифмическое время, возрастает очень медленно.
Хуже всего со сложностью обстоят дела у O (n2) — квадратичного времени.
Два остальных класса сложности быстро возрастают.

1.1.2. Примеры

При небольшом количестве входных данных разница между О (1) и О (n2) пренебрежимо мала. Допустим, у нас есть алгоритм, которому нужно обработать 2000 элементов.

Алгоритму с О (1) для этого потребуется 1 операция.
O (log (n)) — 7 операций.
O (n) — 2000 операций.
O (n*log (n)) — 14 000 операций.
O (n2) — 4 000 000 операций.

Кажется, что разница между О (1) и O (n2) огромна, но на деле вы потеряете не более 2 мс. Глазом моргнуть не успеете, в буквальном смысле. Современные процессоры выполняют сотни миллионов операций в секунду, и именно поэтому во многих проектах разработчики пренебрегают оптимизацией производительности.

Но возьмём теперь 1 000 000 элементов, что не слишком много по меркам БД:

Алгоритму с О (1) для обработки потребуется 1 операция.
O (log (n)) — 14 операций.
O (n) — 1 000 000 операций.
O (n*log (n)) — 14 000 000 операций.
O (n2) — 1 000 000 000 000 операций.

В случае с последними двумя алгоритмами можно будет успеть выпить кофе. А если добавить ещё один 0 к количеству элементов, то за время обработки можно и вздремнуть.

1.1.3. Ещё немного подробностей

Чтобы вы могли ориентироваться:

Поиск элемента в хорошей хэш-таблице занимает О (1).
В хорошо сбалансированном дереве — O (log (n)).
В массиве — O (n).
Наилучшие алгоритмы сортировки имеют сложность O (n*log (n)).
Плохие алгоритмы сортировки — O (n2).

Ниже мы рассмотрим эти алгоритмы и структуры данных.

Существует несколько классов временнόй сложности:

Средняя сложность
Сложность в наилучшем случае
Сложность в наихудшем случае

Чаще всего встречается третий класс. Кстати, понятие «сложности» применимо также к потреблению алгоритмом памяти и операций ввода/вывода дисковой системы.

Существуют сложности куда хуже, чем n2:

n4: характерно для некоторых плохих алгоритмов.
3n: ещё хуже! Ниже будет рассмотрен один алгоритм с подобной временнόй сложностью.
n!: вообще адский треш. Замучаетесь ждать результат даже на небольших объёмах данных.
nn: если вы дождались результата выполнения этого алгоритма, то впору задаться вопросом, а стоит ли вам вообще этим заниматься?

1.2. Сортировка слиянием

Что вы делаете, когда вам нужно отсортировать коллекцию? Вызываете функцию sort (), верно? Но понимаете ли вы, как она работает?

Есть несколько хороших алгоритмов сортировки, но здесь мы рассмотрим только один из них: сортировку слиянием. Возможно, сейчас вам это знание не кажется полезным, но вы поменяете мнение после глав про оптимизацию запросов. Более того, понимание работы этого алгоритма поможет понять принцип важной операции — соединение слиянием.

1.2.1. Слияние

В основе алгоритма сортировки слиянием лежит одна хитрость: для слияния двух отсортированных массивов размером N/2 каждый требуется всего лишь N операций, называющихся слиянием.

Рассмотрим пример операции слияния:

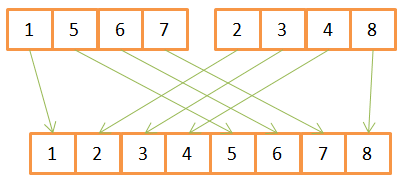
Как видите, для создания отсортированного массива из 8 элементов, для каждого из них нужно провести по одной итерации в двух исходных массивах. Поскольку они уже заранее отсортированы, то:

Сначала в них сравниваются имеющиеся элементы,
наименьший из них переносится в новый массив,
а затем происходит возврат в тот массив, откуда был взят предыдущий элемент.
Шаги 1–3 повторяются до тех пор, пока в одном из исходных массивов не останется лишь один элемент.
После этого из второго массива переносятся все оставшиеся элементы.

Данный алгоритм хорошо работает лишь потому, что оба исходных массива были заранее отсортированы, поэтому ему не нужно возвращаться в их начало во время очередной итерации.

Пример псевдокода сортировки слиянием:

array mergeSort(array a)
   if(length(a)==1)
      return a[0];
   end if

   //recursive calls
   [left_array right_array] := split_into_2_equally_sized_arrays(a);
   array new_left_array := mergeSort(left_array);
   array new_right_array := mergeSort(right_array);

   //merging the 2 small ordered arrays into a big one
   array result := merge(new_left_array,new_right_array);
   return result;

Данный алгоритм разбивает задачу на ряд маленьких подзадач (парадигма «разделяй и властвуй»). Если вы не поняли сути, то попробуйте представить, что алгоритм состоит из двух фаз:

Фаза деления — массив делится на более мелкие массивы.
Фаза сортировки — мелкие массивы собираются вместе (сливаются).

1.2.2. Фаза деления

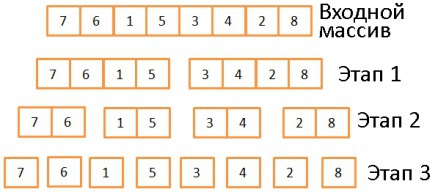
В три этапа исходный массив делится на подмассивы, состоящие из одного элемента. Вообще, количество этапов деления определяется как log (N) (в данном случае N=8, log (N) = 3). Идея в том, чтобы на каждом этапе делить входящие массивы пополам. То есть описывается логарифмом с основанием 2.

1.2.3. Фаза сортировки

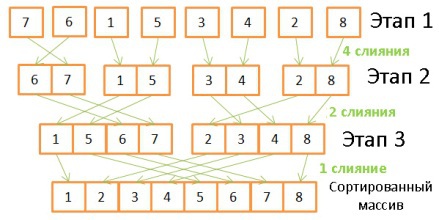
Здесь происходит обратная операция, объединение массивов с двукратным увеличением их размеров. Для этого требуется проделать на каждом этапе по 8 операций:

На первом этапе происходит 4 слияния, по 2 операции каждое.
На втором — 2 слияния по 4 операции.
На третьем — 1 слияние из 8 операций.

Поскольку количество этапов определяется как log (N), то общее количество операций определяется как N * log (N).

1.2.4. Возможности сортировки слиянием

В чём преимущества данного алгоритма?

Его можно модифицировать для уменьшения потребления памяти, если вы хотите не создавать новые массивы, а модифицировать входящий (так называемый «алгоритм замещения»).
Его можно модифицировать для уменьшения потребления памяти и использования дисковой подсистемы, снизив количество операций ввода/вывода. Идея заключается в том, что в памяти находятся только те части данных, которые подвергаются обработке в конкретный момент времени. Это особенно важно, когда нужно сортировать многогигабайтные таблицы, а в наличии есть только буфер мегабайт на 100. Данный алгоритм называется «внешняя сортировкой».
Его можно модифицировать для запуска в нескольких параллельных процессах/потоках/серверах
Например, распределённая сортировка слиянием является ключевой особенностью Hadoop.

Этот алгоритм может практически превращать свинец в золото! Он используется в большинстве (если не во всех) СУБД, хотя и не он один. Если вас интересует больше грязных подробностей, можете почитать одну исследовательскую работу, в которой разбираются плюсы и минусы распространённых алгоритмов сортировки.

1.3. Массив, дерево и хэш-таблица

Итак, с временнόй сложностью и сортировкой разобрались. Теперь давайте обсудим три структуры данных, на которых держатся современные БД.

1.3.1. Массив

Двумерный массив — простейшая структура данных. Таблица может быть представлена в виде массива:

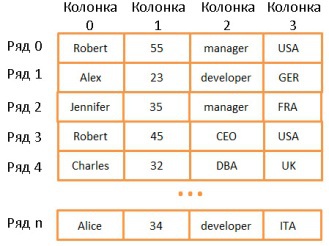
Здесь каждая строка представляет собой какой-то объект, колонка — свойство объекта. Причём разные колонки содержат разные типы данных (целые числа, строки, даты и т.д.).

Это очень удобный способ хранения и визуализации информации, но очень неподходящий для случаев, когда нужно найти какое-то конкретное значение. Допустим, вам нужно найти всех сотрудников, работающих в Великобритании. Для этого придётся просмотреть все строки, чтобы найти те, где имеется значение «UK». На это потребуется N операций (N — количество строк). Не так уж и плохо, но хорошо бы и побыстрее. И здесь нам помогут деревья.

Примечание: большинство современных СУБД используют продвинутые виды массивы, позволяющие эффективнее хранить таблицы (например, на основе куч или индексов). Но это не решает проблему скорости поиска по колонкам.

1.3.2. Дерево и индекс БД

Бинарное дерево поиска — это дерево, в котором ключ в каждом узле должен быть:

Больше, чем любой из ключей в ветке слева.
Меньше, чем любой из ключей в ветке справа.

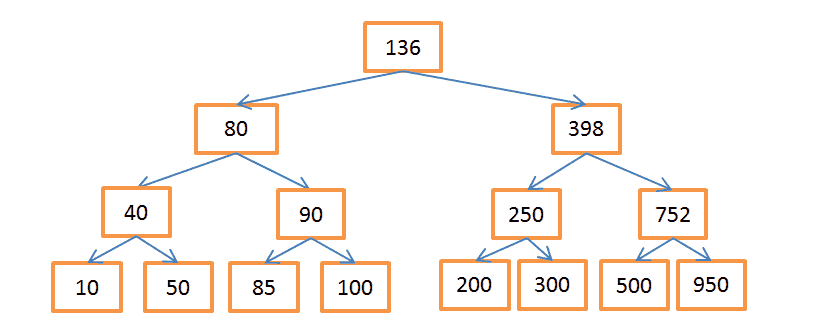
Каждый узел представляет собой указатель на строку в связанной таблице.

Вышеприведённое дерево содержит N = 15 элементов. Допустим, нам нужно найти узел со значением 208:

Начнём с узла, содержащего ключ 136. Поскольку 136 < 208, то следуем по правой ветке дерева.
398 > 208, значит спускаемся по левой ветке, исходящей из этого узла.
250 > 208, опять идём по левой ветке.
200 < 208, нужно пойти по правой ветке. Но поскольку у узла с ключом 200 нет веток, то искомое значение не существует. Если бы оно существовало, то у узла-200 были бы ветки.

Допустим, теперь нужно найти узел со значением 40:

Опять начинаем с корневого узла-136. Раз 136 > 40, значит идём по левой ветке.
80 > 40, снова «поворачиваем налево».
40 = 40, такой узел существует. Извлекаем ID строки, хранящийся в этом узле (это не значение ключа), и ищем по нему в связанной таблице.
Зная ID строки, можно очень быстро извлечь нужные данные.

Каждая процедура поиска состоит из определённого количества операций по мере путешествия по ветвям дерева. Количество операций определяется как Log (N), так же как и в случае с сортировкой слиянием.

Но вернёмся к нашей проблеме.

Допустим, у нас есть строковые значения, соответствующие названиям разных государств. Соответственно и узлы дерева содержат строковые ключи. Чтобы найти сотрудников, работающих в «UK», нужно просмотреть все узлы, чтобы найти соответствующий, и извлечь из него ID всех строк, содержащих данное значение. В отличие от поиска по массиву, здесь нам потребуется всего log (N) операций. Описанная конструкция называется индексом БД.

Такой индекс можно создать для любой группы колонок (для строковых, целочисленных, их комбинаций, дат и т.д.), если у вас есть функция для сравнения ключей (т.е. групп колонок). Таким образом вы можете распределить ключи в определённом порядке.

Индекс В+дерева

Несмотря на высокую скорость поиска, дерево плохо работает в случаях, когда нужно получить несколько элементов в пределах двух значений. Временнáя сложность будет равна О (N), потому что нам придётся просмотреть каждый узел и сравнить его с заданными условиями. Более того, данная процедура требует большого количества операций ввода/вывода, ведь нужно считывать всё дерево. То есть нам нужен более эффективный способ запроса диапазона. В современных БД для этого используется модифицированная версия дерева — В+дерево. Его особенность в том, что информацию (ID строк связанной таблицы) хранят лишь самые нижние узлы («листья»), а все остальные узлы предназначены для оптимизации поиска по дереву.

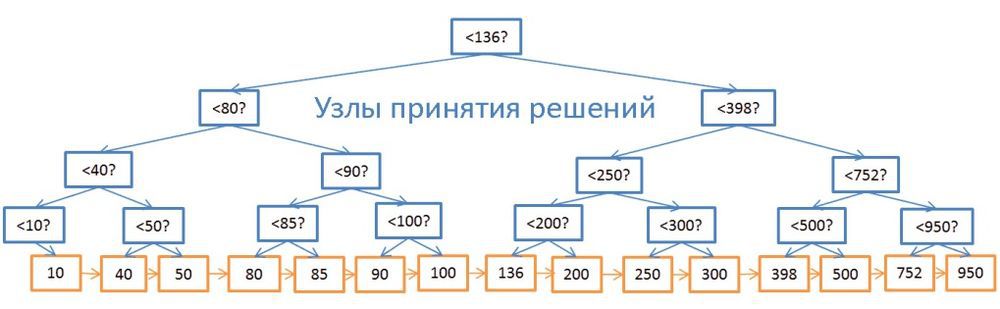
Как видите, здесь вдвое больше узлов. «Узлы принятия решений» помогают найти нужные узлы, содержащие ID строк в таблице. Но сложность поиска всё ещё равна О (log (N)) (добавился один уровень узлов). Однако главной особенностью B-дерева является то, что «листья» образуют наследственные связи.

Допустим, нам нужно найти значения в диапазоне от 40 до 100:

Сначала ищем всё, что больше 40 или значения, ближайшего к нему, если 40 не существует. Совсем как в обычном дереве.
А затем, с помощью связей наследования, выбираем всё, что меньше 100.

Пусть дерево содержит N узлов, и нам нужно выбрать М наследников. Для поиска конкретного узла потребуется log (N) операций, как и в обычном дереве. Но найдя его, мы тратим только М операций на поиск М наследников. То есть суммарно нам потребуется М + log (N) операций, в отличие от N в случае с обычным деревом. Нам даже не нужно считывать дерево целиком, а только М + log (N) узлов, так что дисковая система задействуется меньше. Если значение М невелико (например, 200), а N — напротив, большое, (1 000 000), то выигрыш в скорости поиска будет очень значителен.

Но есть ложка дёгтя на этом празднике жизни. Если вы добавляете или убираете строки в БД, а, следовательно, и в связанном индексе В+дерева, то:

Необходимо сохранять порядок размещения узлов внутри В-дерева, иначе вы ничего не сможете найти.
Нужно, чтобы В+дерево состояло из как можно меньшего количества уровней, иначе временнáя сложность будет не О (log (N)), а О (N).

Иными словами, В+дерево должно быть самоуправляемым и самобалансирующимся. В связи с низкоуровневой оптимизацией, В+деревья должны быть полностью сбалансированы. К счастью, всё это можно сделать с помощью операций «умного» удаления и вставки. Но за это приходится платить: операции вставки и удаления в В+дереве имеют сложность О (log (N)). Так что наверняка многим из вас знаком такой совет: не надо увлекаться созданием большого количества индексов. В противном случае сильно падает производительность при добавлении/обновлении/удалении строк, поскольку БД приходится актуализировать и всевозможные индексы, а каждый из них требует О (log (N)) операций. К тому же индексы увеличивают нагрузку на диспетчер транзакций, об этом мы поговорим ниже.

Подробнее о В+деревьях можно почитать на Википедии, а также в статьях (один, два) от ведущих разработчиков MySQL. В них рассказывается о том, как InnoDB (движок MySQL) работает с индексами.

1.3.3. Хэш-таблица

Эта структура данных очень полезна для случаев, когда особенно важна скорость поиска. Понимание работы хэш-таблицы необходимо для последующего понимания такой важной операции, как хэш-соединение (hash join). Хэш-таблица зачастую используется для хранения некоторых внутренних данных (таблицы блокировок, буферного пула). Данная структура используется для быстрого поиска элементов по их ключам. Для построения хэш-таблицы нужны:

Ключ для каждого элемента.
Хэш-функция, вычисляющая хэши по ключам. Хэши ещё называют блоками.
Функция сравнения ключей. Найдя правильный блок, мы можем с помощью этой функции найти искомый элемент внутри блока.

Вот пример простой хэш-таблицы:

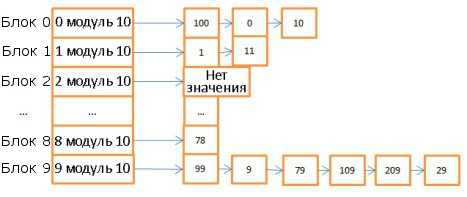
Здесь 10 блоков, в качестве хэш-функции брался модуль 10 от значения ключа. То есть для поиска нужного блока достаточно знать последнюю цифру значения ключа: если это 0, то элемент хранится в корзине 0, если 1, то в корзине 1, и т.д. В качестве функции сравнения используется операция сравнения двух целочисленных.

Допустим, нам нужно найти элемент 78:

Хэш-таблица вычисляет значение хэша, оно равно 8.
Обращаемся к блоку 8 и сразу находим искомый элемент.

То есть мы затратили всего две операции: на вычисление хэша и на поиск внутри блока.

Теперь поищем элемент 59:
Вычисляем хэш, он равен 9.
Обращаемся к блоку 9, первый элемент равен 99. Поскольку 99 на равно 59, то сравниваем со вторым элементом (9), потом с третьим (79), и так далее вплоть до последнего (29).
Искомый элемент отсутствует.

Итого мы затратили 7 операций.

Как видите, скорость поиска зависит от искомого значения. Изменим хэш-функцию, будет вычислять хэши по модулю 1 000 000 (то есть берём последние 6 цифр). В этом случае на поиск элемента 59 уйдёт лишь одна операция, поскольку в блоке 000059 нет никаких элементов. Поэтому крайне важно подобрать удачную хэш-функцию, которая будет генерировать блоки с очень небольшим количеством элементов.

В вышеприведённом примере нетрудно подобрать подходящий вариант. Но это слишком простой случай. Гораздо труднее выбрать хэш-функцию, если ключи:

Строковые (например, фамилии).
Двойные строковые (имена и фамилии).
Двойные строковые с датой (добавляются даты рождения)

и т.д.
Но если вам удалось подобрать хорошую хэш-функцию, то сложность поиска по таблице будет равна О (1).

Массив против хэш-таблицы

Почему бы не использовать одни массивы? Дело в том, что:

Хэш-таблицу можно загрузить в память наполовину, а остальное оставить на диске.
В случае с массивом вам придётся использовать смежное пространство памяти. И если вы загружаете большую таблицу, то очень сложно обеспечить достаточный объём этого самого смежного пространства.
Вы можете выбрать любые ключи для хэш-таблицы. Например, название государства И фамилию человека.

За подробностями можете обратиться к статье о Java HashMap, это пример эффективной реализации хэш-таблицы. Для этого вам не нужно разбираться в Java, если что.
Мы рассмотрели базовые компоненты БД. Теперь давайте отойдём назад и окинем взглядом всю картину.

БД представляет собой совокупность информации, к которой можно легко получить доступ и модифицировать. Но то же самое можно сказать и о группе файлов. По сути, простейшие БД, наподобие SQLite, как раз и представляют собой лишь кучки файлов. Но тут важно, как именно эти файлы организованы внутри и связаны между собой, поскольку SQLite позволяет:

Использовать транзакции для обеспечения сохранности и связанности данных.
Быстро обрабатывать данные вне зависимости от их объёма.

В общем виде структуру БД можно представить так:

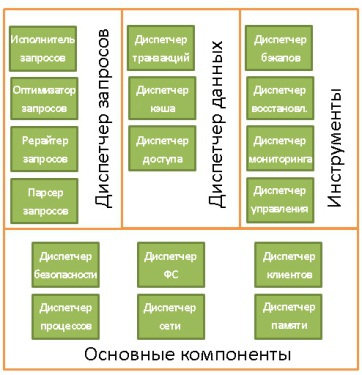
На самом деле, существует куча разных представлений о том, как может выглядеть структура БД. Так что не надо зацикливаться на данной иллюстрации. Нужно лишь усвоить, что БД состоит из различных компонентов, взаимодействующих между собой.

Основные компоненты БД (Core Components):

Диспетчер процессов. Во многих БД имеется пул процессов/потоков, которыми нужно управлять. Причём в погоне за производительностью некоторые БД используются свои собственные потоки, а не предоставляемые ОС.
Диспетчер сети. Пропускная способность сети имеет большое значение, особенно для распределённых БД.
Диспетчер файловой системы. Первым «бутылочным горлышком» любой БД является производительность дисковой подсистемы. Поэтому очень важно иметь диспетчер, который идеально работает с файловой системой ОС или даже заменяет её.
Диспетчер памяти. Чтобы не упереться в невысокую производительность дисковой подсистемы, нужно иметь много оперативной памяти. А значит, нужно эффективно ею управлять, что и делает данный диспетчер. Особенно когда у вас много одновременных запросов, использующих память.
Диспетчер безопасности. Управляет аутентификацией и авторизацией пользователей.
Диспетчер клиентов. Управляет клиентскими соединениями.

Инструменты (Tools):

Диспетчер резервного копирования. Назначение очевидно.
Диспетчер восстановления. Используется для восстановления когерентного состояния БД после сбоя.
Диспетчер мониторинга. Занимается протоколированием всех активностей внутри БД и используется для наблюдения за её состоянием.
Диспетчер общего управления. Хранит метаданные (вроде наименований и структуры таблиц) и используется для управления базами, схемами, табличными пространствами и т.д.

Диспетчер запросов (Query Manager):

Парсер запросов. Проверяет их валидность.
Рерайтер запросов. Осуществляет предварительную оптимизацию.
Оптимизатор запросов.
Исполнитель запросов. Компилирует и исполняет.

Диспетчер данных (Data Manager):

Диспетчер транзакций. Занимается их обработкой.
Диспетчер кэша. Используется для отправки данных перед использованием и перед записью на диск.
Диспетчер доступа к данным. Управляет доступом к данным в дисковой подсистеме.

Далее мы рассмотрим, как БД управляет SQL-запросами с помощью:

Диспетчера клиентов.
Диспетчера запросов.
Диспетчера данных.

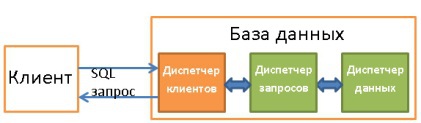
Используется для управления соединениями с клиентами — веб-серверами или конечными пользователями/приложениями. Диспетчер клиентов обеспечивает разные способы доступа к БД с помощью как всем известных API (JDBC, ODBC, OLE-DB и т.д.), так и с помощью проприетарных.

Когда вы подключаетесь к БД:

Диспетчер сначала аутентифицирует вас (проверят логин и пароль), а потом авторизует для использования БД. Эти права доступа определяются вашим DBA.
Далее диспетчер проверяет, есть ли доступный процесс (или поток), который может обработать ваш запрос.
Также он сверяет, не находится ли база в состоянии высокой нагрузки.
Диспетчер может подождать, пока не высвободятся нужные ресурсы. Если период ожидания закончился, а они не высвободились, диспетчер закрывает соединение с сообщением об ошибке.
Если же ресурсы имеются, то диспетчер перенаправляет ваш запрос диспетчеру запросов.
Поскольку диспетчер клиентов передаёт и получает данные от диспетчера запросов, то он сохраняет их в буфере частями и отправляет вам.
При возникновении проблемы диспетчер прерывает соединение с каким-то объяснением и высвобождает ресурсы.

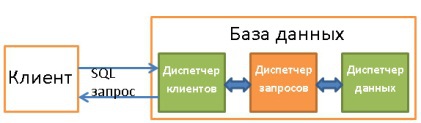
Именно он является сердцем БД. Здесь все плохо написанные запросы превращаются в быстроисполняемый код, затем происходит исполнение, а результат отправляется диспетчеру клиентов. Описанный процесс состоит из нескольких этапов:

Запрос сначала проверяется на валидность (парсится).
Затем он перезаписывается с целью исключения бесполезных операций и предварительной оптимизации.
Далее производится окончательная оптимизация для повышения производительности. После этого запрос трансформируется в план исполнения и доступа к данным.
План компилируется.
И исполняется.

Если вы хотите узнать больше, то можете изучить следующие материалы:

Access Path Selection in a Relational Database Management System. Статья 1979 года посвящена оптимизации.
Очень хорошая и глубокая презентация о том, как DB2 9.x оптимизирует запросы.
Не менее хорошая презентация о том, как тем же самым занимается PostgreSQL. Здесь информация подана в наиболее понятной форме.
Официальная документация SQL по оптимизации. Читается довольно легко, поскольку SQLite используется простые правила. К тому же это единственный официальный документ по данной теме.
Хорошая презентация о том, как SQL Server 2005 оптимизирует запросы.
Официальный документ об оптимизации в Oracle 12c.
Два теоретических курса по оптимизации запросов от автора книги «Database System Concepts»: первый и второй. Хороший материал, акцентирующий внимание на экономии операций ввода/вывода. Но для усвоения требуется хорошо владеть CS.
Ещё один теоретический курс, более доступный для понимания. Но он посвящён операторам объединения и управлению операциями ввода/вывода.

4.1. Парсер запросов

Каждый SQL-оператор отправляется в парсер и проверяется на правильность синтаксиса. Если вы сделаете ошибку в запросе, то парсер его отклонит. Например, напишете SLECT вместо SELECT.

Но этим функции парсера не ограничиваются. Он также проверяет, чтобы ключевые слова использовались в правильном порядке. Например, если WHERE будет идти до SELECT, то запрос будет отклонён.

Также парсер анализирует таблицы и их поля внутри запроса. Он использует метаданные БД для проверки:

Самого факта существования таблицы.
Наличия в ней полей.
Возможности осуществления операций с полями имеющихся типов. Например, нельзя сравнивать целочисленные со строковыми, или использовать функцию substring () применительно к целочисленному).

Далее парсер проверяет, имеете ли вы вообще право читать (или записывать) таблицы в запросе. Эти права доступа также задаются вашим DBA.

В ходе всех этих проверок SQL-запрос трансформируется во внутреннее представление (чаще всего в дерево). Если всё в порядке, то оно отправляется в рерайтер запросов.

4.2. Рерайтер запросов

В его задачи входит:

Предварительная оптимизация запроса.
Исключение ненужных операций.
Помощь оптимизатору в поиске наилучшего возможного решения.

Рерайтер применяет к запросу список известных правил. Если запрос всем им удовлетворяет, то он перезаписывается. Вот некоторые из этих правил:

Слияние представлений (видов). Если вы используете в запросе представление, то оно трансформируется с помощью SQL-кода.
Сведение подзапросов. Наличие подзапросов сильно затрудняет оптимизацию, так что рерайтер старается так модифицировать запрос, чтобы избавиться от подзапросов.

Например, этот запрос:

SELECT PERSON.*
FROM PERSON
WHERE PERSON.person_key IN
(SELECT MAILS.person_key
FROM MAILS
WHERE MAILS.mail LIKE 'christophe%');

будет заменён на:

SELECT PERSON.*
FROM PERSON, MAILS
WHERE PERSON.person_key = MAILS.person_key
and MAILS.mail LIKE 'christophe%';

Исключение ненужных операций. Допустим, вы используете DISTINCT несмотря на то, что у вас применяется условие UNIQUE, предотвращающее появление не уникальных данных. В этом случае ключевое слово DISTINCT удаляется парсером.
Предотвращение ненужных объединений. Если вы дважды указали одно и то же условие объединения, поскольку одно из них было скрыто в представлении, или просто бессмысленно из-за транзитивности, то оно удаляется.
Арифметические вычисления. Если вы пишете что-то, требующее вычисления, то оно делается однократно в ходе перезаписи. Скажем, WHERE AGE > 10+2 трансформируется в WHERE AGE > 12. А TODATE (какая-то дата) заменяется на дату в соответствующем формате.
Partition pruning. Если вы используете партиционированные таблицы, рерайтер может найти подходящие партиции.
Перезапись материализованного представления. Если у вас есть материализованное представление, совпадающее с подмножеством предикатов в запросе, то рерайтер проверяет, является ли представление актуальным, и модифицирует запрос так, чтобы он использовал материализованное представление вместо таблиц.
Особые правила. Если у вас специфические правила модификации запроса (вроде политик Oracle), то рерайтер может их применить.
OLAP-трансформации. Трансформируются функции анализа/кадрирования, звездообразные объединения, свёртывание и т.д. Поскольку рерайтер и оптимизатор очень тесно взаимодействуют, то, скорее всего, OLAP-трансформации может осуществлять и оптимизатор, на усмотрение БД.

После применения политик запрос отправляется в оптимизатор, и там начинается самое веселье.

4.3. Статистика

Прежде чем перейти к рассмотрению оптимизирования запросов, давайте поговорим о статистике, поскольку без неё БД становится совершенно безмозглой. Если вы не скажете ей проанализировать собственные данные, она этого и не сделает, сделав очень плохие допущения.

Какого рода информация нужна БД?

Сначала давайте вспомним, как БД и ОС хранят данные. Для этого они используют такие минимально возможные сущности, как страницы или блоки (размером по 4 или 8 Кбайт по умолчанию). Если вам нужно сохранить 1 Кбайт, то на это всё-равно уйдёт целая страница. То есть вы попусту тратите много места в памяти и на диске.

Вернёмся к нашей статистике. Когда вы просите БД собрать статистику, она:

Подсчитывает количество строк/страниц в таблице.
Для каждой колонки:
- Считает количество уникальных значений.
- Определяет длину значений данных (мин, макс, среднее).
- Определяет диапазон значений данных (мин, макс, среднее).
Собирает информацию об индексах БД.

Вся эта информация помогает оптимизатору спрогнозировать количество операций ввода/вывода, а также потребление ресурсов процессора и памяти при исполнении запроса.

Очень большое значение имеет статистика по каждой колонке. Например, нам нужно в таблице объединить две колонки: «фамилия» и «имя». Благодаря статистике БД знает, что в ней содержится 1 000 уникальных значений «имя» и 1 000 000 — «фамилия». Поэтому база объединит данные именно в таком порядке — «фамилия, имя», а не «имя, фамилия»: это требует гораздо меньше операций сравнения, поскольку вероятность совпадения фамилий гораздо ниже, и в большинстве случаев для сравнения достаточно брать 2–3 первые буквы фамилии.

Но всё это базовая статистика. Можно также попросить БД собрать дополнительную статистику и построить гистограммы. Они дают представление о распределении значений внутри колонок. Например, определить самые часто встречающиеся значения, квантили и т.д. Эта дополнительная статистика помогает БД ещё лучше планировать запрос. Особенно в случае с предикатами равенства (WHERE AGE=18) или предикатами диапазонов (WHERE AGE > 10 AND AGE < 40), поскольку БД будет лучше представлять количество колонок, имеющих отношение к этим предикатам (селективность, избирательность).

Статистика хранится в виде метаданных. Например, вы можете найти её в:

Oracle: USER/ALL/DBA_TABLES и USER/ALL/DBA_TAB_COLUMNS
DB2: SYSCAT.TABLES и SYSCAT.COLUMNS

Статистику нужно регулярно обновлять. Нет ничего хуже, чем БД, считающая, что состоит из 500 строк, в то время как в ней их 1 000 000. К сожалению, на сбор статистики уходит некоторое время, поэтому в большинстве БД по умолчанию эта операция не выполняется автоматически. Когда у вас миллионы записей, то собрать по ним статистику довольно затруднительно. В этом случае можно собирать только базовую информацию, или брать небольшую часть базы (например, 10%) и собирать по ней полную статистику. Но тут есть риск того, что оставшаяся часть данных может существенно отличаться, и значит ваша статистика окажется нерепрезентативной. А это приведёт к неправильному планированию запроса и увеличению времени его исполнения.

Если вы хотите узнать больше о статистике, читайте документацию к своим БД. Лучше всего это описано для PostgreSQL.

4.4. Оптимизатор запросов

Все современные БД используют CBO (Cost Based Optimization), стоимостную оптимизацию. Суть её заключается в том, что для каждой операции определяется её «стоимость», а затем общая стоимость запроса уменьшается с помощью использования наиболее «дешёвых» цепочек операций.

Для лучшего понимания стоимостной оптимизации мы рассмотрим три распространённых способа объединения двух таблиц и увидим, как даже простой запрос на объединение может превратиться в кошмар для&n