[Перевод] Как определить массу Земли с помощью шаров и веревки
Иллюстрация: Daniel Grizely / Getty Images
Занятно думать о том, каким способом мы узнаём что-то. Например, масса Солнца составляет около 2×1030 кг. Это такое огромное число, что его трудно осознать. И если нам так сложно даже вообразить такие большие числа, как мы будем искать эти значения? Что ж, первоначальный метод заключался в использовании небольших масс, палки и веревки. Пожалуй, это один из важных шагов в определении массы как Солнца, так и всех планет в нашей Солнечной системе. Это эксперимент Кавендиша, впервые проведенный Генри Кавендишем в 1798 году. Эксперимент действительно крутой, поэтому я собираюсь объяснить, как он работает.
Между объектами, обладающими массой, существует гравитационное притяжение. У баскетбольного мяча есть гравитационное взаимодействие с Землей (поскольку они оба имеют массу). Именно это гравитационное взаимодействие заставляет баскетбольный мяч ускоряться, когда он падает на землю, если вы его отпустите. Естественно, все всегда знали, что если отпустить предмет, он упадет. Однако только примерно во времена Ньютона люди осознали, что это притяжение также действует между астрономическими объектами, такими как Земля, Луна и Солнце. Это дает нам модель взаимодействия сил, которую часто называют законом всемирного тяготения Ньютона, но, как и у большинства крупных идей, у нее наверняка было много соавторов.
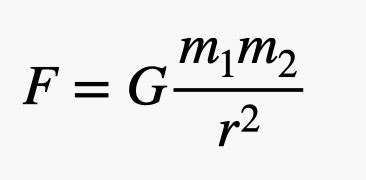
Иллюстрация: RHETT ALLAIN
Давайте рассмотрим эту модель гравитационной силы. Во-первых, величина этой силы зависит от произведения двух взаимодействующих масс (m1 и m2). Во-вторых, величина уменьшается пропорционально квадрату расстояния между двумя объектами (r). Наконец, есть G. Это универсальная гравитационная постоянная. Это ключ к определению массы Земли.
Итак, давайте сделаем шаг назад на мгновение. Когда мы измеряем вещи, нам всегда приходится делать какой-то выбор. Если мы хотим получить массу в килограммах, то мы должны решить, как указать значение 1 кг. Можно сказать, что килограмм — это масса 1 литра воды. Конечно, это не лучшее определение (теперь у нас есть методы получше). Хорошо, а как насчет измерения силы? Мы используем единицу под названием Ньютон, где 1 Ньютон — это сила, необходимая для ускорения тела, массой 1 килограмм, на 1 метр на секунду в квадрате. Да, ситуация выходит из-под контроля, но главное то, что вы можете дать эти определения и построить одну единицу измерения на другой.
А теперь представьте себе этот эксперимент. Предположим, я беру литр воды (который, как я знаю, составляет 1 килограмм) и измеряю гравитационную силу, исходящую от Земли. Если я знаю радиус Земли (греки прекрасно справились с его вычислением) и гравитационную постоянную G, то я могу решить уравнение гравитационной силы для массы Земли (см.выше). Но что такое гравитационная постоянная? Это сложная часть, и вот как вы можете найти значение G.
Оказывается, эта гравитационная постоянная очень мала. Это означает, что притяжение между двумя обычными объектами, такими как бутылки с водой, до смешного ничтожно мало. Единственный способ получить заметную гравитационную силу — это если одна из взаимодействующих масс огромна (как Земля). Однако есть способ разобраться — использовать крутильные весы.
Начнем с простой демонстрации физики, которую вы можете попробовать дома. Возьмите карандаш и поместите его на край стола так, чтобы примерно половина карандаша свешивалась с края, будто он вот-вот упадет, но держится. В этот момент карандаш в основном балансирует прямо на краю стола. Карандаш поддерживает только эта крошечная точка контакта, поэтому сила трения не может вызвать крутящий момент, чтобы остановить его вращение. Даже сверхмалое усилие, прижимающее конец карандаша, заставит его вращаться. Стоит едва подуть, чтобы карандаш начал вращаться.

Видео: RHETT ALLAIN
Мне нравится подносить пальцы к карандашу и притворяться, будто я использую свои супергеройские способности, чтобы двигать его. Теперь давайте заменим карандаш более длинной палкой, и вместо того, чтобы класть ее на стол, я бы повесил ее на веревке. Поскольку она опирается на середину, достаточно крошечной силы чтобы заставить ее вращаться, как и в случае с карандашом. Вместо того, чтобы дуть, мы могли бы заставить небольшую гравитационную силу двигать ее. Вот как это работает.
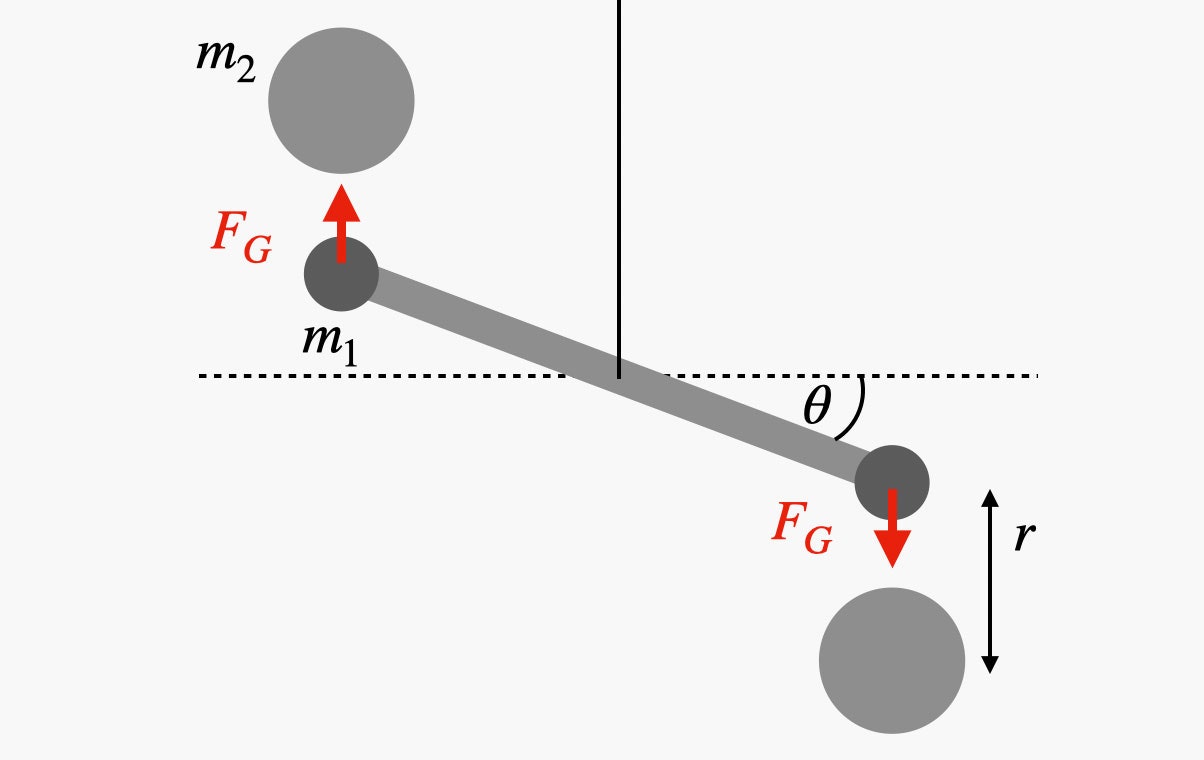
Иллюстрация: RHETT ALLAIN
На конце вращающегося горизонтального стержня есть две меньшие массы (обозначенные m1). Эти массы взаимодействуют с большими массами (m2), которые находятся на расстоянии (r) от них. Горизонтальный стержень в конечном итоге достигнет некоторого положения равновесия, поскольку из-за скручивания троса, который поддерживает стержень, возникает небольшой крутящий момент. Трос действует как вращающаяся пружина. Чем больше он скручивается, тем больше крутящий момент. Если вы знаете соотношение между углом поворота (θ) и крутящим моментом, вы можете вычислить гравитационную силу, притягивающую массу на конце палки к большей неподвижной массе. В конфигурации на диаграмме выше большие массы заставят палку вращаться по часовой стрелке (как видно сверху). Если вы переместите бóльшие массы на другую сторону от палки, гравитационные силы заставят ее вращаться против часовой стрелки. Это показывает, что вращение происходит из-за гравитационного взаимодействия между парными массами. Как только палка займет устойчивое положение, останется лишь измерить массы и расстояние между ними, чтобы получить гравитационную постоянную.
В этом случае мы получаем гравитационную постоянную G = 6,67×10–11N*m2 кг2. Вы можете видеть, что эта константа действительно очень мала. В качестве примера мы можем продемонстрировать, как производится вычисление. Предположим, что вы человек, стоящий на расстоянии 1 метра от другого человека такой же массы (около 75 кг). Какая величина силы будет действовать на вас из-за гравитационного притяжения? Подставляя эти значения (вместе с константой) в уравнение силы мы получаем:
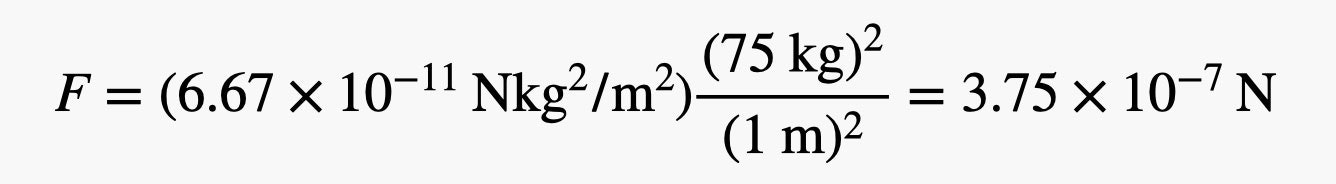
Иллюстрация: RHETT ALLAIN
Но в этом нет смысла. Никто не может почувствовать настолько небольшую силу. Попробуем представить ситуацию с силой, сопоставимой с гравитационным притяжением между двумя людьми. Как вам такое? Предположим, вы кладете в руку небольшой предмет. Вы можете почувствовать гравитационную силу Земли на этом объекте, потому что ваша рука должна толкать его вверх, чтобы уравновесить гравитационную силу. Объект какой массы создаст вызванную Землей гравитационную силу, равную силе притяжения между двумя людьми? На поверхности Земли некоторые из этих значений всегда одинаковы (гравитационная постоянная, масса Земли и расстояние до центра Земли). Мы можем сгруппировать все эти значения в одно число.
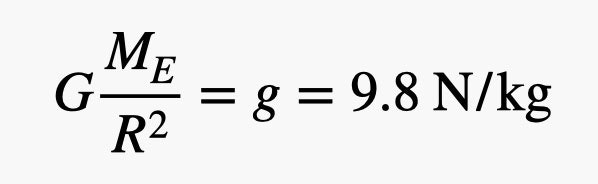
Иллюстрация: RHETT ALLAIN
Мы можем назвать это локальной гравитационной постоянной Земли (local-Earth gravitational constant). Все, что вам нужно сделать, это взять массу и умножить на «g» (мы используем строчную букву «g», чтобы ее не путать с другой гравитационной постоянной «G»), и вы получите гравитационную силу (вес). В этом случае вам понадобится объект массой около 4×10–11 грамм, чтобы получить вес, равный силе притяжения между двумя людьми. Это все еще слишком мало для того, чтобы понять. А если так? Человеческие волосы могут иметь линейную массовую плотность 6,5 граммов на километр (информация из этой публикации). Это означает, волос длиной всего 6×10–6 миллиметров имеет вес, равный притяжению между двумя людьми. Это уму непостижимо. Вот вам бонус, мои расчеты, если вы хотите изменить значения.
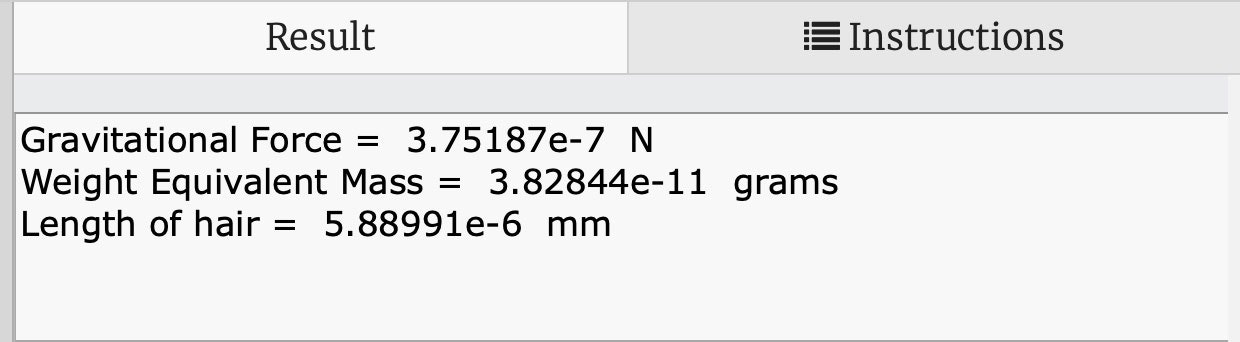
Иллюстрация: RHETT ALLAIN
О, да, вы можете повторить тот же самый расчет, но использовать известную массу и вычислить массу Земли. Получится около 5,97×1024 килограмма. Но зачем останавливаться на достигнутом? Вы также можете использовать значение G, чтобы найти массу солнца. Я кратко объясню, как работает этот расчет.
Итак, у вас есть планета, подобная Меркурию, которая вращается вокруг Солнца. Если учесть, что орбита круговая, то на Меркурий действует гравитационная сила со стороны Солнца.
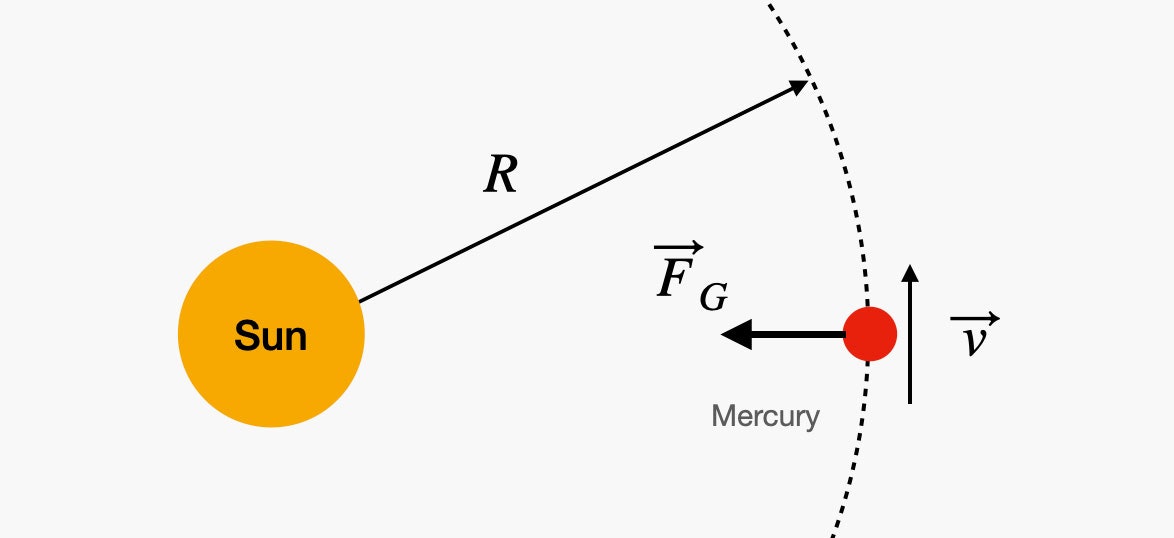
Иллюстрация: RHETT ALLAIN
Гравитационная сила заставляет планету ускоряться и двигаться по кругу (центростремительное ускорение). Но это центростремительное ускорение зависит как от угловой скорости (ω), так и от орбитального расстояния (R). Поскольку на планете действует только одна сила (гравитационная сила), она будет равна массе, умноженной на ускорение, и в результате получится следующее соотношение.
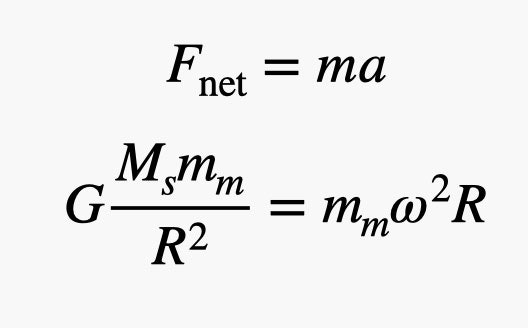
Иллюстрация: RHETT ALLAIN
Обратите внимание: здесь предполагается, что солнце неподвижно, что, в целом, верно. Масса Солнца колоссальна по сравнению с массой Меркурия, так что масса Меркурия не имеет значения. Итак, решение для нахождения массы солнца:
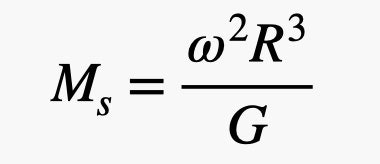
Иллюстрация: RHETT ALLAIN
Теперь вам просто нужно найти расстояние от точки орбиты до центра Меркурия. Вы можете сделать это, начав с радиуса Земли. Затем вам нужно найти угловую скорость — вы можете получить её, посмотрев, сколько времени требуется Меркурию, чтобы совершить полный оборот вокруг Солнца. После этого все готово. У вас есть гравитационная постоянная, и вы можете вычислить массу Солнца. Удивительно, что все это начнется с каких-то небольших масс на горизонтально вращающейся палке, но это правда.
