[Перевод] Как я научил ИИ играть в Tetris для NES. Часть 2: ИИ28.08.2018 11:48

Первая часть (анализ кода) находится здесь: https://habr.com/post/420725/.

Алгоритм

Описание

Алгоритм непрерывно выполняет следующие шаги:

1. Ждёт, пока не создастся новое тетримино.
2. Проверяет тип нового созданного тетримино, тип следующего тетримино (фигура в поле предпросмотра) и содержимое игрового поля.
3. Исследует все возможные способы добавления двух тетримино на игровое поле и оценивает каждую вероятность.
4. Перемещает новое созданное тетримино, чтобы оно совпадало с местом наилучшенней обнаруженной вероятности.

Каждый из этих этапов подробно описан ниже.

Поиск блокировки

Рассмотрим упрощённую версию Tetris, в которой фигуры не падают автоматически. Единственный способ спустить фигуру вниз — это мягкий спуск. Убрав из игры тайминги, мы можем полностью описать состояние активного тетримино его позицией и ориентацией. Фигура имеет известное место изначального создания, а для преобразования из одного состояния в другое используются следующие операции:

• Перемещение на один шаг вниз
• Перемещение на один шаг влево
• Перемещение на один шаг вправо
• Поворот на один шаг против часовой стрелки
• Поворот на один шаг по часовой стрелке

Эти операции применимы только тогда, когда квадраты получившегося тетримино соответствуют пустым ячейкам игрового поля. Когда переместиться на один шаг вниз невозможно, состояние считается заблокированным. Однако поскольку мы упростили Tetris и ожидание блокировки по сути является бесконечным, то заблокированное состояние можно далее преобразовывать другими операциями, выполняя скольжения и прокручивания.

Множество заблокированных состояний с минимальной последовательностью создающих их операций можно найти с помощью поиска в ширину (breadth-first search, BFS). Как сказано ниже, для хранения промежуточных результатов он использует очередь.

1. Заносим в очередь состояние при создании.
2. Выводим из очереди состояние.
3. Получаем последующие состояния, применяя операции преобразования.
4. Если среди них нет перемещения вниз, то выведенное из очереди состояние является заблокированным.
5. Заносим в очередь последующие состояния, которые мы ещё не посетили.
6. Если очередь не пуста, повторяем с шага 2.

Программа представляет каждое состояние в виде объекта со следующими полями:

{ x, y, rotation, visited, predecessor }

В процессе подготовки программа создаёт трёхмерный массив объектов состояний (20 строк × 10 столбцов × 4 поворотов), инициализируя соответствующим образом x, y и rotation.

Поле visited помечается, когда состояние занесено в очередь. В BFS это допустимо, потому что каждое последующее состояние увеличивает общую длину пути на 1. То есть увеличением длины пути невозможно создать последующее состояние, которое нужно вставить куда-то, кроме конца очереди для сохранения порядка.

Поле predecessor указывает на объект состояния, из которого происходит текущее состояние. Оно задано, когда состояние занесено в очередь. Состояние создания не имеет предшествующих состояний.

Множество блокированных состояний, обнаруженное во время поиска, определяется типом тетримино и заполненными блоками на игровом поле. Последовательность сгенерировавших их ходов можно выяснить (в обратном порядке), переходя по ссылкам predecessor к состоянию создания. Когда константе PLAY_FAST в начале программы присваивается значение true, она полностью пропускает предшествующие состояния, напрямую кладя тетримино на поле и блокируя его.

Трёхмерный массив объектов состояний, очередь и BFS упакованы в класс. У него есть метод поиска, получающий игровое поле (двухмерный массив), тип тетримино и слушателя. Каждый раз, когда обнаруживается блокированное состояние, игровое поле обновляется, добавляя тетримино в соответствующее место. Затем изменённое игровое поле вместе с информацией об изменениях передаётся слушателю для обработки. После того, как слушатель выполнит возврат, игровое поле восстанавливается.

Слушатель используется для объединения нескольких операций поиска в цепочку, что даёт возможность нахождения всех возможных способов добавления двух (или более) тетримино на игровое поле. Первый поисковик в цепочке выполняет BFS только один раз. Однако второй поисковик выполняет BFS каждый раз, когда первый поиск обнаруживает заблокированное состояние. И так далее, если в цепочке присутствуют и другие поисковики.

Слушатель последнего поисковика оценивает изменившееся игровое поле. Когда он находит игровое поле лучше того, что было исследовано ранее, он записывает используемый объект заблокированного состояния, который в это время использует первый поисковик в цепочке. Поскольку первый поисковик выполняет BFS только один раз, поля predecessor его объектов состояния остаются правильными до завершения всего процесса поиска. То есть последний слушатель по сути записывает путь, по которому должно пойти первое тетримино, чтобы в результате прийти к наилучшей конфигурации игрового поля.

Оценочная функция

Изменённому игровому полю оценочная функция присваивает значение — взвешенную сумму различных влияющих параметров. Используемая в этом случае оценочная функция основана на функции, разработанной Исламом Эл-Аши. В ней используются следующие параметры:

• Общее количество очищенных рядов: это общее количество рядов, которые будут очищены вследствие добавления двух тетримино.
• Общая высота блокировки: высота блокировки — это высота над полом игрового поля, на которой блокируется фигура. Это вертикальное расстояние, на которое бы упала заблокированная фигура, если убрать все остальные занятые квадраты игрового поля и сохранить ориентацию фигуры. Общая высота блокировки — это сумма высот блокировки двух тетримино.
• Общее количество ячеек-«колодцев»: ячейка-колодец — это пустая ячейка, расположенная над всеми занятыми ячейками в столбце так, что её левый и правый сосед являются занятыми ячейками; при определении колодцев стенки игрового поля считаются занятыми ячейками. Идея заключается в том, что колодец — это структура, открытая сверху, закрытая снизу и окружённая стенами с обеих сторон. Вероятность прерывающихся пробелов в стенках колодца означает, что ячейки-колодцы не обязательно возникают в непрерывной куче в пределах столбца.
• Общее количество отверстий в столбцах: отверстие в столбце — это пустая ячейка, расположенная непосредственно под занятой ячейкой. Пол игрового поля не сравнивается с ячейкой над ним. В пустых столбцах отверстий нет.
• Общее количество переходов в столбцах: переход в столбцах — это пустая ячейка, соседствующая с занятой ячейкой (или наоборот) в пределах одного столбца. Сочетание самого верхнего занятого блока столбца с пустым пространством над ним не считается переходом. Аналогичным образом, пол игрового поля тоже не сравнивается с ячейкой над ним. Следовательно, в совершенно пустом столбце нет переходов.
• Общее количество переходов в строках: переход в строках — это пустая ячейка, соседствующая с занятой ячейкой (или наоборот) в пределах одного ряда. Пустые ячейки рядом со стенками игрового поля считаются переходами. Общее количество высчитывается для всех строк игрового поля. Однако совершенно пустые строки не учитываются в общем количестве переходов.

Эль-Аши предположил, что полезные веса можно найти с помощью алгоритма «метод роя частиц» (particle swarm optimization, PSO), который итеративно усовершенствует совокупность вариантов решений имитацией наблюдаемого в природе поведения роя. В нашем случае каждый вариант решения является вектором весов, а приспособленность варианта определяется игрой в Tetris; это общее количество тетримино, на протяжении которых он выживал до конца игры.

Эти идеи применены в описанной ниже версии на Java; она выполняется за пределами FCEUX и её можно настроить для неграфической, расположенной в памяти игры, работающей с гораздо более высокой скоростью. После подготовки PSO я удивился, увидев, что алгоритм не движется дальше после начальной итерации. После этой итерации несколько случайно сгенерированных вариантов решения уже играли достаточно хорошо. В течение нескольких дней размер этого множества снижался, пока не остался только один вариант. Вот значения для этого решения:

Параметр	Вес
Общее количество очищенных рядов	1.000000000000000
Общая высота блокировки	12.885008263218383
Общее количество ячеек-колодцев	15.842707182438396
Общее количество отверстий в столбцах	26.894496507795950
Общее количество переходов в столбцах	27.616914062397015
Общее количество переходов в строках	30.185110719279040

Игровое поле оценивалось умножением параметров на соответствующие им веса и сложением результатов. Чем ниже значение, тем лучше решение. Поскольку все параметры и веса имеют положительные значения, то все параметры вредят общей оценке; каждый из них необходимо минимизировать. Также это означает, что наилучшая оценка равна 0.

Поскольку эти веса выбирались случайным образом, диапазон подходящих значений может быть очень широк. Этот конкретный набор чисел и предполагаемая относительная важность каждого параметра могут быть несущественными. Тем не менее, интересно будет за ними внимательно понаблюдать.

Наименее вредящий параметр — это общее количество очищенных рядов. Сам факт того, что этот параметр вредит, контринтуитивен. Но основная цель ИИ — это выживание. Он не стремится к наибольшему количеству очков. Вместо этого он играет консервативно, обычно очищая ряды по одному. Для получения Double, Triple или Tetris придётся выращивать кучу, что идёт вразрез с долговременной целью.

Следующей в списке идёт общая высота блокировки. Её можно минимизировать, опуская тетримино как можно ближе к полу. Это простая стратегия, вносящая свой вклад в долговременной перспективе в выживание, а в кратковременной перспективе — в качественную упаковку фигур.

Вес, назначенный общему количеству ячеек-колодцев, кажется немного удивительным, потому что опытные игроки обычно намеренно строят глубокие колодцы, чтобы набрать несколько Tetris (комбинаций из четырёх линий) подряд. Но как сказано выше, это рискованная игра, противоречащая основной цели — выживанию. Кроме того, количество колодцев является показателем «неровности» кучи. Определённый уровень неровности идёт на пользу при размещении определённых фигур или комбинаций фигур. Но высокая неровность причиняет ущерб плотной упаковке.

Общее количество отверстий в столбцах равно примерно половине от общего количества переходов в столбцах. Эти параметры можно скомбинировать и свернуть в общий связанный параметр, получив более обширный и наиболее вредный параметр: общее количество переходов.

Области плотной упаковки имеют во всех направлениях малое количество переходов. Поэтому основную стратегию, движущую искусственным интеллектом, можно вкратце описать так: упаковывать фигуры как можно более близко друг к другу.

Другие параметры

Вот список ещё нескольких параметров, с которыми я экспериментировал в процессе разработки ИИ:

• Высота кучи: занятые блоки могут нависать над пустыми ячейками, создавая выступы и отверстия; однако зафиксировать занятые блоки над совершенно пустыми строками невозможно. Следовательно, высота кучи — это количество строк, в которых содержится хотя бы один занятый блок.
• Общее количество занятых столбцов: это количество столбцов, в которых содержится хотя бы одна занятая ячейка.
• Общее количество занятых ячеек: количество занятых ячеек на игровом поле.
• Общее количество соединённых областей: здесь применяется алгоритм заливки для подсчёта количества непрерывно связанных областей. Кроме нахождения занятых «островов», он обнаруживает отверстия, растянувшиеся по обеим осям.
• Дисперсия высоты столбцов: это статистическая мера величины разброса высот столбцов. Является показателем неровности поверхности.
• Общая величина адаптации: вычисление величины адаптации кучи под следующую неизвестную фигуру. Она подсчитывает общее количество способов, которыми 7 типов фигур можно добавить на игровое поле без появления новых отверстий. Для точного подсчёта потребуется многократное применение BFS. Но для приближенного подсчёта дерево поиска можно сильно усечь.
• Средняя оценка следующей фигуры: этот параметр углубляет поиск благодаря анализу всех возможностей для следующей неизвестной фигуры. Он использует другие парамтеры для отдельного расположения каждого типа фигур, а затем возвращает среднее для 7 оценок. Для каждого размещения фигуры требуется выполнение BFS.
• Усреднённая симулируемая игра: параметр симулирует серию партий в Tetris, подбирая фигуры с помощью собственного генератора псевдослучайных чисел и применяя для работы с ними ИИ. В конце каждой партии игровое поле оценивается с помощью других параметров. Возвращается усреднённое значение для всех партий.

Все параметры можно настраивать, если добавить настраиваемые факторы. Например, вместо простого подсчёта очищенных рядов можно назначить собственные веса для Single, Double, Triple и Tetris, сымитировав систему очков. Если одновременная очистка нескольких рядов вредит долговременной цели выживания, то одиночным рядам можно назначить отрицательный вес, а другие могут получить положительные.

Ещё одним полезным фактором является значение смещения. Например, совершенно плоская поверхность кучи имеет дисперсию высот столбцов 0. Но идеально плоская поверхность не адаптируется под S и Z, а также другие сочетания фигур. Следовательно, с помощью вычитания константы дисперсию необходимо центрировать около оптимальной неровности.

Настроенные и смещённые параметры можно возводить в какую-нибудь степень, чтобы перед вычислением взвешенной суммы они могли масштабироваться логарифмически или экспоненциально. Все эти вероятности можно рассматривать как дополнительные веса, которые потенциально можно оптимизировать методами наподобие PSO.

Многие из параметров дают понимание того, насколько хорошо куча сможет управляться с дополнительными фигурами, например, те, которые имеют дело с неровностью поверхности, но «Общая величина адаптации», «Средняя оценка следующей фигуры» и «Усреднённая симулируемая игра» оценивают изменённое игровое поле вставкой фигур, не входящих в две известные. При исследовании последующих фигур из-за быстрого устранения рядов количество полученного дополнительного знания уменьшается с глубиной. Это значит, что давно прошедшее течение партии не так важно, и течение партии в далёком будущем тоже не очень важно. На самом деле, если короткая последовательность фигур случайным образом поставлена неправильно, то ИИ быстро восстанавливает ход игры, используя несколько следующих фигур для очистки затронутых рядов. Определение оптимальной величины анализа последующих фигур требует дальнейших исследований.

Ещё одним аспектом полезности параметра являются вычислительные затраты. Затраты сильно увеличиваются, потому что оценочная функция вызывается для каждого возможного размещения двух фигур. Поскольку ИИ должен уметь играть в Tetris в реальном времени, затратные факторы, предоставляющие ценную информацию, можно обменять на более приближенные техники, которые выполняются быстрее.

Обучение ИИ

Существуют патологические последовательности, которые способны привести к Game Over вне зависимости от стратегии. Простейший пример — это бесконечная последовательность тетримино S и Z, которая, как показано в анимации, быстро приводит ИИ к проигрышу.

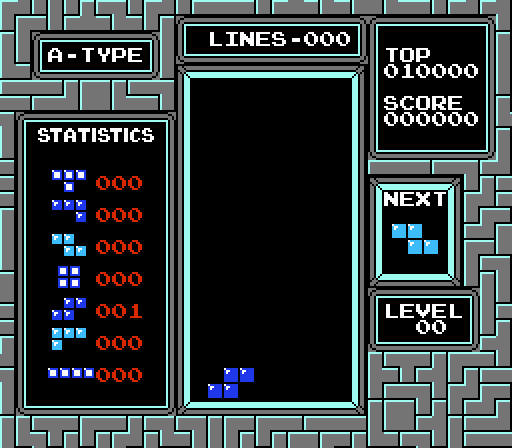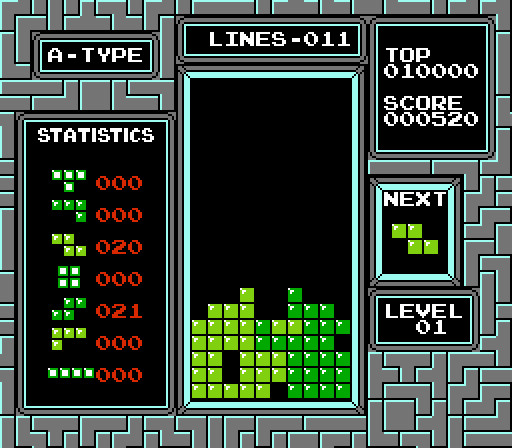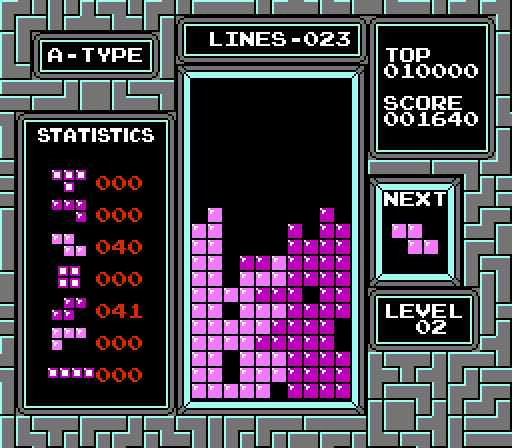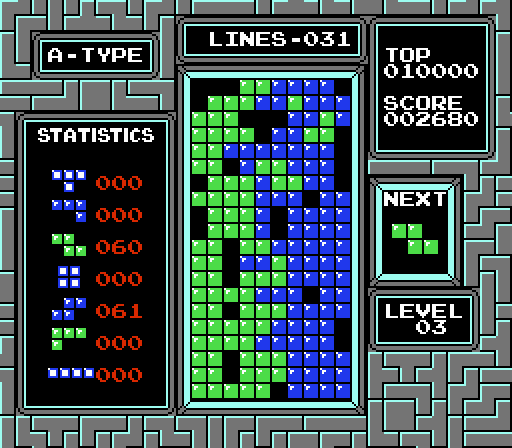
Поскольку для прогона варианта ИИ до завершения нескольких партий и вычисления среднего нужны дни, совершенно непрактично использовать как метрику управления PSO среднюю длительность партии. Вместо этого можно с контролируемой скоростью увеличивать сложность игры, повышая частоту S и Z, что со временем приведёт к попеременному созданию только этой пары фигур.

Я попробовал использовать этот метод обучения, но обнаружил, что обучение ИИ работе с частыми S и Z на самом деле вредит способности справляться с равномерно распределёнными случайными фигурами.

В альтернативном методе, на который меня вдохновила игра B-Type, управляющей PSO метрикой является частота очистки рядов. Игровое поле представляет собой схему из 10 строк случайных мусорных блоков, и при каждой очистке строки снизу появляется новая строка мусора, восстанавливая высоту кучи. Так как игровое поле имеет ширину 10 столбцов, а каждое тетримино состоит из 4 квадратов, то в среднем AI должен очищать ряд через каждые 2,5 тетримино. А чтобы избавляться от мусора, он должен делать это ещё быстрее.

К сожалению, эта техника тоже не улучшила производительность. Одна из вероятных причин заключается в том, что случайные дыры в мусоре не точно соответствуют тем строкам, с которыми ИИ имеет дело в настоящем игровом процессе. Кроме того, очистка ряда — это кратковременная цель; жадная очистка рядов необязательно улучшит долговременное выживание. Время от времени ряды не стоит трогать, чтобы обрабатывать определённые комбинации последующих фигур.

На своей веб-странице Колин Фэй предложил другой подход. Он создал гистограммы, отображающие процент фигур, блокируемых в каждой строке во время пробных партий. Интересно, что все гистограммы выглядят практически идентично вне зависимости от количества созданных фигур. Исходя из этого, он предположил, что можно использовать приближенное изображение функции для любой пробной партии при оценке статистического ожидания блокировки фигуры в строке создания, получив таким образом время, в течение которого ИИ будет играть до конца игры. Я решил исследовать эту возможность.

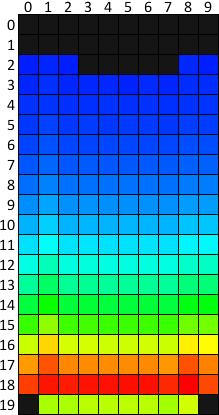
Ниже показана тепловая карта множества пробных партий, в сумме содержащих 2 039 900 000 тетримино. Каждая ячейка раскрашена на основании процента заблокированных в ней фигур. Для усиления визуального контраста выбрана нелинейная палитра. Карта была создана нормализацией значений ячеек с помощью деления на максимальный процент ячеек, а затем возвещением в степень 0,19 (см. «гамма-коррекция»).

Цвет Процент ■ 0.00000000 ■ 0.00000315 ■ 0.00024227 ■ 0.00307038 ■ 0.01860818 ■ 0.07527774 ■ 0.23582574 ■ 0.61928352 ■ 1.42923040 ■ 2.98867416 ■ 5.78182519

Тёмно-оранжевая и красная полоса в строках 17 и 18 означает, что подавляющее большинство фигур в результате оказываются там. Бледно-зелёный оттенок снизу — следствие геометрии фигур: только 4 из 7 типов тетримино могут оказаться в нижней строке. Нижние углы чёрные, потому что там невозможно оказаться.

Цвет вдоль каждой строки практически однороден, и это позволяет предположить, что горизонтально фигуры распределяются равномерно. Незначительные разрывы можно объяснить, посмотрев на гистограммы отдельных типов фигур:

T оказывается наиболее универсальным типом: его гистограмма более равномерна, чем у всех остальных. Аномалии в гистограмме J — результат влияния стенок; только Jr и Jl могут находиться в боковых столбцах, что заставляет ИИ для компенсации чаще использовать столбцы 1 и 9. То же самое относится и к L. Гистограммы Z и S выглядят примерно одинаковыми, что подчёркивает дисбаланс из-за того, что Zv и Sv не являются идеальными зеркальными отражениями друг друга. Тип O ограничен игровым полем 19×9, и похоже, что ИИ склонен чаще использовать O по бокам, чем в центре. Тетримино I сдвинуто вправо, потому что там расположена его исходная точка; поэтому блокировка в столбце 1 случается редко.

В таблице показано процентное соотношение фигур, блокируемых в каждой строке.

Строка	Процент
0	0.0000000000
1	0.0000000000
2	0.0000004902
3	0.0000026472
4	0.0000066180
5	0.0000172557
6	0.0000512280
7	0.0001759400
8	0.0006681210
9	0.0023187901
10	0.0077928820
11	0.0259672043
12	0.0866187068
13	0.2901315751
14	0.9771663807
15	3.3000408353
16	10.6989059268
17	28.5687976371
18	50.0335706162
19	6.0077671454

Вот график значений:

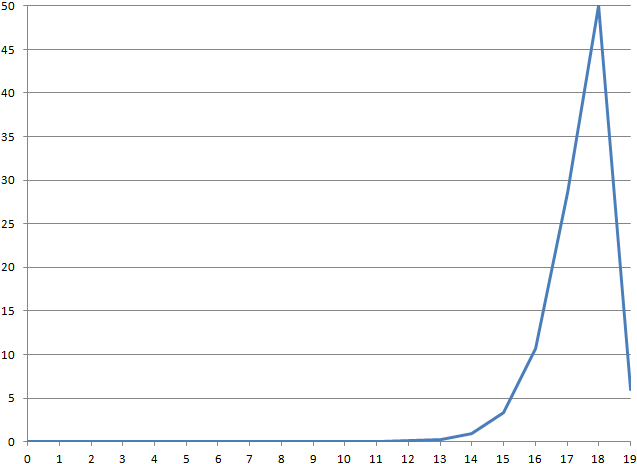
Если не учитывать строку 19, то график демонстрирует экспоненциальный рост.

Ниже показан список соотношений количества заблокированых фигур в соседних строках.

СтрокаA/Строка B	Соотношение (%)
½	0.00
2/3	18.52
¾	40.00
4/5	38.35
5/6	33.68
6/7	29.12
7/8	26.33
8/9	28.81
9/10	29.76
10/11	30.01
11/12	29.98
12/13	29.85
13/14	29.69
14/15	29.61
15/16	30.84
16/17	37.45
17/18	57.10
18/19	832.81

В строках 16–19 учитываются фигуры, взаимодействующие с полом игрового поля, поэтому их можно отбросить. В строках 0–5 слишком выборка слишком мала, чтобы быть значимой. Оставшиеся соотношения, пары 6/7–14/15, почти идентичны; их среднее значение равно 29.24%. Это значит, что вероятность того, что куча вырастет на одну строку примерно одинакова вне зависимости от высоты кучи. Это вполне логично, потому что правила Tetris ограничивают вазаимодействия в вершине кучи при её плотной упаковке.

Ниже показан график log10 процентов фигур в строках 6–15.

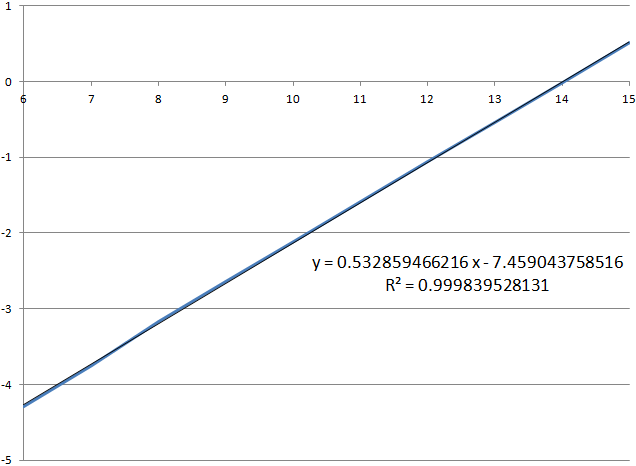
Он близок к идеально прямой линии с близким к 1 коэффициентом детерминации. Формула, выведенная из показанной выше линейной регрессии, даёт нам пересечение с осью Y, предполагающее, что процент фигур в строке 0 приблизительно равен 10−7.459%. Величина, обратная этому значению, даёт нам статистическое ожидание в 2 877 688 349 тетримино или 1 151 075 340 рядов до конца игры.

Это даёт нам понять, что log10 процента фигур в каждой строке остаётся линейным вплоть до строки 0. Однако когда куча почти достигает потолка игрового поля, свобода перемещения ограничивается до такой степени, что это свойство нарушается. Кроме того, блокировка фигуры в строке 0 не обязательно означает game over; ещё можно спастись, если есть место для создания новых фигур.

Ещё один способ оценки силы ИИ заключается в измерении среднего количества созданных фигур между полными очистками игрового поля. Полную очистку можно получить всего с 5 тетримино. Например, среди прочих возможностей, этого можно добиться выложенными на полу игрового поля пятью фигурами O. В общем случае, поскольку каждое тетримино состоит из 4 квадратов, а ширина игрового поля — 10 квадратов, то количество созданных фигур между полной очисткой должно быть кратным 5 (так как 4×5n = 2×10n).

У моего ИИ среднее количество созданных фигур между полными очистками поля равно 1181 — довольно небольшое число. Поскольку полная очистка аналогична перезапуску игры, полную партию можно рассматривать как чрезвычайно долгую серию перезапусков игры, за которым следует быстрое продвижение к game over. Как и описанная выше последовательность попеременных S-Z, приводящие к завершению игры патологические последовательности обычно очень коротки.

На гистограмме ниже показана вероятность (в процентах) того, что ИИ достигнет полной очистки поля после указанного количества созданных фигур.

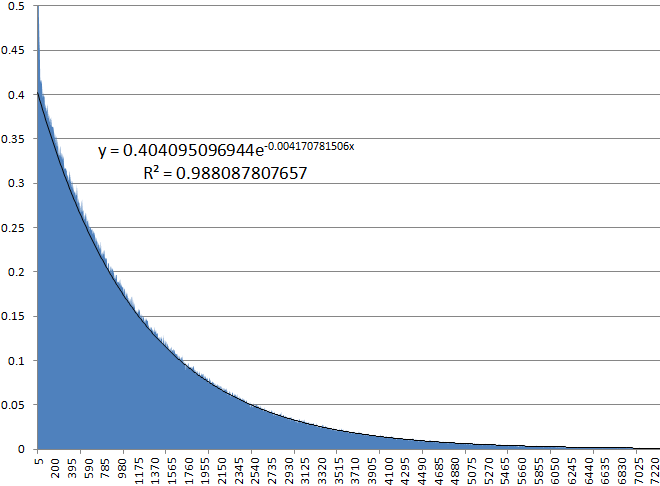
Порядок степени в показанной выше формуле определяет скорость убывания и, предположительно, силу ИИ. Согласно этой формуле, примерно 0,4% или около 1 из 253 партий, начинающихся с пустого игрового поля, завершаются полной очисткой через всего 5 тетримино.

В противоположность тому, что предпололожил Фэй, константы в линейном и экспоненциальном приближениях требуют очень большого размера выборки, чтобы R2 приблизилось к 1, поэтому этот способ неприменим для PSO. Однако константы, полученные при долгих партиях, можно использовать для оптимизации функции аппроксимации, создающей возможные значения констант при коротких партиях. В своего рода петле обратной связи разработки оптимизированную функцию аппроксимации можно использовать в PSO, который усовершенствует ИИ, который в свою очередь можно использовать для вычисления новых констант, служащие в качестве эталонных критериев для функции аппроксимации.

Версия на Java

О программе

Для разработчиков, незнакомых с Lua, я добавил в zip-файл с исходниками порт ИИ на Java. Классы являются почти построчной трансляцией объектов Lua на основе замыканий.

Пакеты

Код разделён на два пакета:

• tetris.ai содержит классы и интерфейсы ИИ.
• tetris.gui создаёт графическую модель игрового поля.

Классы и интерфейсы ИИ

Класс с соответствующим названием Tetriminos описывает тетримино. Он используется подобное enum и содержит константы для всех типов тетримино:

public static final int NONE = -1;
public static final int T = 0;
public static final int J = 1;
public static final int Z = 2;
public static final int O = 3;
public static final int S = 4;
public static final int L = 5;
public static final int I = 6;

NONE означает неназначенное значение. Оно используется для пустых ячеек игрового поля.

Также в Tetriminos содержатся две модели таблицы ориентаций. PATTERNS — это 4-мерный массив integer (тип × поворот × квадрат × координаты), содержащий относительные координаты квадратов; строки упорядочены так, что в каждом типе ориентация создания фигуры является первой. ORIENTATIONS — это другая модель, 2-двухмерный массив (тип × поворот) объектов Orientation. Каждый Orientation содержит координаты квадрата как массив объектов Point. Также в нём есть поля, описывающие интервал разрешённых позиций для соответствующей ориентации.

public class Orientation {
  public Point[] squares = new Point[4];
  public int minX;
  public int maxX;
  public int maxY;
  ...
}

public class Point {
  public int x;
  public int y;
  ...
}

Поворот тетримино (второй индекс в обеих таблицах ориентаций) используется в объектах State, которыми манипулирует BFS.

public class State {
  public int x;
  public int y;
  public int rotation;
  public int visited;
  public State predecessor; 
  public State next;
  ...
}

x, y и rotation совместно описывают позицию и ориентацию фигуры. Так как тип тетримино остаётся постоянным с момента создания до блокировки, поле для него необязательно.

Класс Searcher, в котором содержится алгоритм BFS, создаёт при полный набор всех возможных объектов State при создании:

private void createStates() {
  states = new State[AI.PLAYFIELD_HEIGHT][AI.PLAYFIELD_WIDTH][4];
  for(int y = 0; y < AI.PLAYFIELD_HEIGHT; y++) {
    for(int x = 0; x < AI.PLAYFIELD_WIDTH; x++) {        
      for(int rotation = 0; rotation < 4; rotation++) { 
        states[y][x][rotation] = new State(x, y, rotation);
      }
    }
  }
}

Хотя в Java есть богатый Collections API, Searcher содержит собственную реализацию очереди. Класс Queue использует State.next для соединения объектов State в связанный список. Поскольку все объекты State определены предварительно, а каждый State может быть внесёт в очередь не больше одного раза, то очередь может работать на месте, что позволяет отказаться от излишних временных объектов-контейнеров, используемых в общих реализациях очереди.

«Сердцем» BFS является показанный ниже метод search.

public boolean search(int[][] playfield, int tetriminoType, int id) {

  int maxRotation = Tetriminos.ORIENTATIONS[tetriminoType].length - 1;

  int mark = globalMark++;

  if (!addChild(playfield, tetriminoType, mark, null, 5, 0, 0)) {
    return false;
  }    

  while(queue.isNotEmpty()) {
    State state = queue.dequeue();

    if (maxRotation != 0) {
      addChild(playfield, tetriminoType, mark, state, state.x, state.y, 
          state.rotation == 0 ? maxRotation : state.rotation - 1);
      if (maxRotation != 1) {
        addChild(playfield, tetriminoType, mark, state, state.x, state.y, 
            state.rotation == maxRotation ? 0 : state.rotation + 1);
      }
    }

    addChild(playfield, tetriminoType, mark, state, 
        state.x - 1, state.y, state.rotation);
    addChild(playfield, tetriminoType, mark, state, 
        state.x + 1, state.y, state.rotation);

    if (!addChild(playfield, tetriminoType, mark, state,
        state.x, state.y + 1, state.rotation)) {
      lockTetrimino(playfield, tetriminoType, id, state);
    }
  }

  return true;
}

Он порождает очередь с состоянием созданного тетримино, а затем последовательно извлекает дочерние элементы из выведенных из очереди состояний, добавляя их обратно в очередь, когда они появляются на игровом поле.

В метод search передаются игровое поле, содержащее сочетание занятых и пустых ячеек, создаваемый тип тетримино и произвольный идентификатор. В процессе выполнения BFS при каждом обнаружении позиции блокировки вызывается слушатель.

public interface ISearchListener {  
  public void handleResult(int[][] playfield, int tetriminoType, 
      int id, State state);
}

Слушатель получает изменившееся игровое поле, содержащее заблокированное на месте тетримино. Также передаются тип создаваемого тетримино и произвольный идентификатор. Последним параметром является State, в котором заблокировано тетримино. Следуя по цепочке ссылок State.predecessor, можно восстановить весь путь обратно к State создания фигуры.

State.visited можно было реализовать как boolean; однако при этом перед поиском потребовалось бы перебирать все объекты State для сброса visited на false. Вместо этого я сделал visited значением int, сравниваемым со счётчиком, увеличивающимся при каждом вызове.

Метод addChild предварительно заносит в очередь последующие состояния. Последующее состояние должно находиться в пределах поля и быть расположенным на 4 пустых ячейках игрового поля. Кроме того, последующее состояние должно быть непосещённым State. Если позиция допустима, addChild возвращает true, даже если последующее состояние не удалось поместить в очередь, потому что его уже посещали.

Метод search использует возвращаемое addChild значение для определения того, можно ли создать фигуру. Если фигуру создать нельзя, то куча достигла вершины и поиск больше выполнять нельзя; поэтому он возвращает false.

Возвращаемое addChild значение также изучается на предмет возможности спуститься ещё на один шаг. Если этого сделать нельзя, то текущее состояние является позицией блокировки и запускается вызов lockTetrimino. Метод lockTetrimino изменяет игровое поле, вызывает слушателя, а затем восстанавливает игровое поле.

Каждая строка массива playfield содержит 1 дополнительный элемент, в котором хранится количество занятых ячеек в строке. Инкремент элемента выполняется методом lockTetrimino, поскольку он помечает ячейки как занятые.

Когда слушатель получает изменённое игровое поле, он вызывает PlayfieldUtil.clearRows для удаления заполненных рядов; метод распознаёт их, сверяясь со значением в дополнительном элементе массива. Для удаления строки код пользуется тем фактом, что в Java двухмерные массивы по сути являются массивами массивов; он просто сдвигает вниз ссылки на строки. PlayfieldUtil содержит свободные строки; он завершает процесс очистки, вставляя вверх ссылку на одну из них. Перед выполнением сдвига индекс очищаемой строки сохраняется в дополнительный элемент строки. Затем ссылка на строку записывается в стек.

Потом слушатель вызывает PlayfieldUtil.restoreRows для отмены изменений, внесённых в игровое поле. Шаги отменяются в обратном порядке. Сначала получается свободная строка из вершины. Затем из стека извлекается заполненная строка и восстанавливается индекс из дополнительного элемента. Он используется для сдвига ссылок строк и для возврата на место удалённой строки. Наконец, восстанавливается дополнительный элемент, ему присваивается значение ширины игрового поля — количества занятых ячеек в заполненном ряду.

В PlayfieldUtil также имеется метод evaluatePlayfield, который вычисляет и записывает 4 параметра оценки в показанный ниже класс-контейнер.

public class PlayfieldEvaluation {
  public int holes;
  public int columnTransitions;
  public int rowTransitions;
  public int wells;
}

Управляет всем этим класс AI. Он содержит два объекта Searcher, соединённых вместе показанным ниже слушателем.

public void handleResult(
    int[][] playfield, int tetriminoType, int id, State state) {

  if (id == 0) {
    result0 = state;
  }

  Orientation orientation 
      = Tetriminos.ORIENTATIONS[tetriminoType][state.rotation];
  int rows = playfieldUtil.clearRows(playfield, state.y);
  int originalTotalRows = totalRows;
  int originalTotalDropHeight = totalDropHeight;
  totalRows += rows;
  totalDropHeight += orientation.maxY - state.y;

  int nextID = id + 1;

  if (nextID == tetriminoIndices.length) {

    playfieldUtil.evaluatePlayfield(playfield, e);

    double fitness = computeFitness();
    if (fitness < bestFitness) {
      bestFitness = fitness;
      bestResult = result0;
    }
  } else {
    searchers[nextID].search(playfield, tetriminoIndices[nextID], nextID);
  }

  totalDropHeight = originalTotalDropHeight;
  totalRows = originalTotalRows;
  playfieldUtil.restoreRows(playfield, rows);
}

Класс AI может обрабатывать любое количество объектов Searcher, но Nintendo Tetris заранее показывает только одну фигуру. Объекты Searcher хранятся в массиве, а показанный выше код служит в качестве их общего слушателя. Произвольный идентификатор, передаваемый в метод Searcher.search, на самом деле является индексом массива, который также является глубиной поиска. При вызове слушателя идентификатор направляет вызов к следующем Searcher в цепочке. Если он достиг конца массива, то оценивает игровое поле. А когда он находит игровое поле с более высокой оценкой приспособленности, то записывает заблокированное State из первого Searcher в цепочке.

AI содержит метод search, получающий игровое поле и массив, содержащий типы создаваемого и следующего тетримино. Он возвращает State, содержащий позицию и поворот, в которых должно блокироваться первое тетримино. Он никак не ориентируется на второе тетримино; при последующем вызове он заново выполняет вычисление оценки. Если куча слишком высока и цепочке Searcher не удаётся разместить оба тетримино, то AI.search вернёт null.

public State s
    
            
© Habrahabr.ru