[Перевод] Javis v0.3 и анимация рядов Фурье17.12.2020 23:47

whajv7unqwf-8bu8ld_qptyoue0.gif

Прошло уже достаточно времени с релиза Javis v0.2, что обсуждалось в соответствующем посте. Там я дал представление о потенциальном будущем этого графического пакета. Мы наконец-то выпустили v0.3, и будущее стало стандартом по умолчанию.

Просто перечислять все изменения, которые мы ввели, вероятно, было бы довольно скучно, так что лучше я создам аккуратную анимацию, а по пути буду объяснить некоторые удивительные штуки про ряды Фурье.

Я думаю, что довольно много людей слышали о рядах Фурье, но не совсем понимали их. И я совершенно уверен, что все еще нахожусь в их числе. Не знаю, будет ли целесообразно использовать этот пост в качестве вступления для тех, кто вообще не в теме, но я постараюсь сделать все возможное. К слову, завидую я этим людям, потому что ряды Фурье — это нечто чрезвычайно увлекательное.

Этот блог в основном предназначен для читателей, которые интересуются Javis и Julia, поэтому я начну с изменений, которые появились в v0.3.


Изменения в v0.3

Наконец-то у нас есть версия способная транспонировать матрицы, или я предпочитаю говорить об общих возможностях морфинга, поскольку транспонирование работает только иногда.
Надо будет по этой теме подробней отписаться. (Ну, скажем, в ноябре… надеюсь)

cwdyze8cemh10hyvsutkys33bam.gif

Что-то, к сожалению, не попало в v0.3, как например объединение объектов в слои, но работа идет полным ходом. Есть уже концептуальный план, осталось найти время, чтобы все закодить, попутно внося возможные изменения.
Еще было обещано поменять имена некоторых ключевых функций, так что надеюсь, что вы либо не использовали Javis v0.2, либо что вы адаптируетесь и довольны изменениями, которые мы провели.

Давайте просто перечислим некоторые из них:

Action и SubAction теперь называются соответственно Object и Action.
Это связано с тем, что Action раньше больше описывал сам объект и мог фактически перемещать его. Мы решили убрать такую возможность чтобы упростить кодовую базу и сделать различие гораздо более четким.

Далее мы упростили BackgroundAction до Background. Больше никаких комментариев по этому поводу

Наконец, мы удалили Translation, Rotation и Scaling и ввели anim_translate, anim_rotate/anim_rotate_around, а также anim_scale, потому что работа с функциями вместо структур кажется более естественной, и название указывает, что мы попутно делаем анимацию, а не статический перевод.

Последнее важное изменение состояло в том, чтобы избавиться от функции javis и странного дизайна, вызывавшего постоянный беспорядок с этими странными массивами.

Теперь просто определяем видео, объекты и действия строка за строкой и, в конце концов, визуализируем видео: 

using Javis
function ground(args...)
    background("black")
    sethue("white")
end

video = Video(800, 400)
Background(1:100, ground)
ball = Object((args...)->circle(O, 100, :fill), Point(-500, 0))
rolling = Action(anim_translate(Point(1000, 0)))
act!(ball, rolling)

render(video; pathname="rolling_ball.gif")

bu7fy-c_zfdvqsqagrteyex8bqa.gif

Думаю, код предельно прозрачен, кроме, может быть, нескольких причуд …

Функция circle принимает центральную точку и радиус, а также действие (здесь :fill). Почему я определяю центр в центре? Я мог бы определить его в Point(-500, 0), но мне нравится думать о том, что объекты центрируются, а затем, перемещаются вокруг оси. Мне кажется, что здесь есть преимущество: объект легко и правильно масштабируется, а также это облегчает вращение.

На самом деле невозможно увидеть вращение круга (в настоящее время мы его не вращаем). Как насчет того, чтобы добавить что-то к кругу, чтобы мы могли различать вращается ли он? 

using Javis
function ground(args...)
    background("black")
    sethue("white")
end

function my_circle(args...)
    circle(O, 100, :fill)
    sethue("black")
    line(O, Point(100, 0), :stroke)
end

video = Video(800, 400)
Background(1:100, ground)
ball = Object(my_circle, Point(-500, 0))
translating = Action(anim_translate(Point(1000, 0)))
rotating = Action(anim_rotate(0.0, 2*2π))
act!(ball, [translating, rotating])

render(video; pathname="rolling_ball_2.gif")

zmncfuiuabsuxkaigtrpt_4qruu.gif

Таки катится. Ладно, возможно, я немного отвлекся, но позже нам это пригодится.

Думаю, в v0.2 было бы довольно трудно сделать линию внутри круга с длиной зависящей от времени. На самом деле, это было возможно с v0.2.2, но я еще не писал об этом, так что это время перемен

using Javis
function ground(args...)
    background("black")
    sethue("white")
end

function my_circle(args...; line_length=0)
    circle(O, 100, :fill)
    sethue("black")
    setline(2)
    line(O, Point(line_length, 0), :stroke)
end

video = Video(800, 400)
Background(1:100, ground)
ball = Object(my_circle, Point(-500, 0))
translating = Action(anim_translate(Point(1000, 0)))
rotating = Action(anim_rotate(0.0, 2*2π))
changing_len = Action(change(:line_length, 0 => 100))
act!(ball, [translating, rotating, changing_len])

render(video; pathname="rolling_ball_3.gif")

ixzpgromlmdvy5pogsnjuwcssjq.gif

Теперь, наконец, можно просто изменять значения непосредственно анимированным способом. Вот мы вроде как и собрали строительные блоки для Фурье


Ряды Фурье

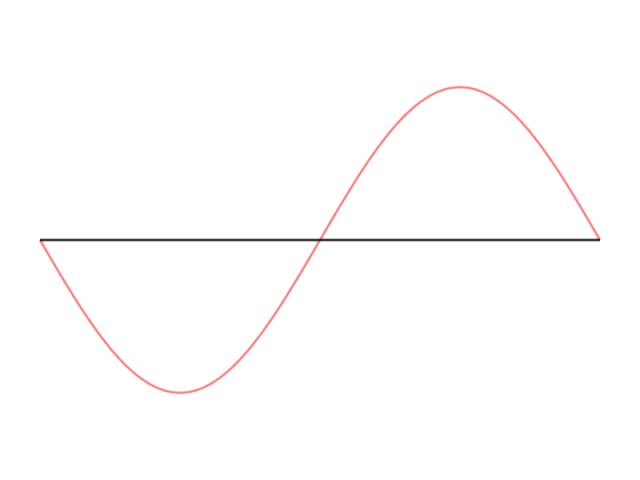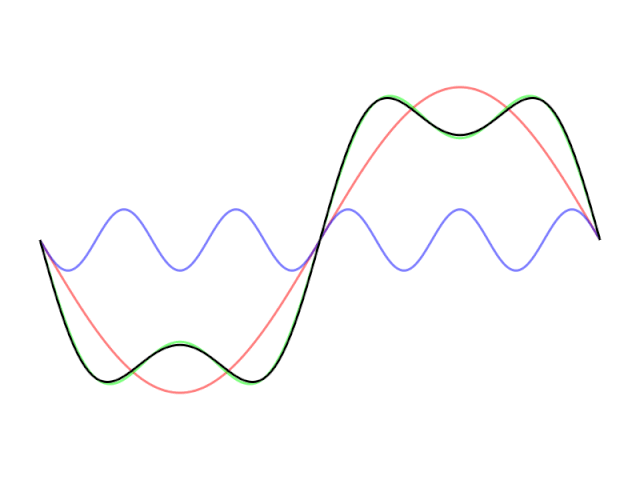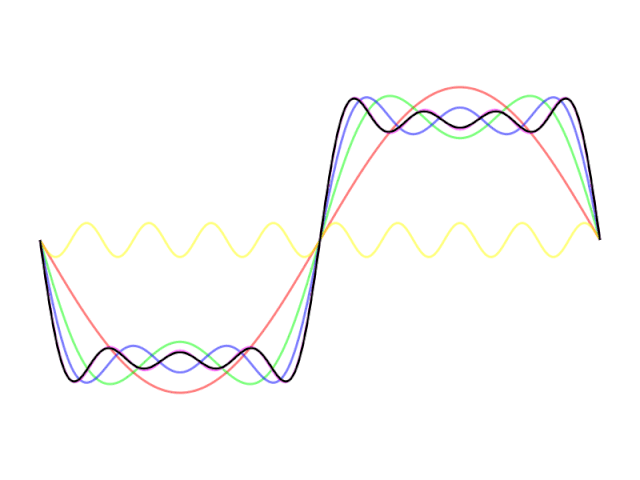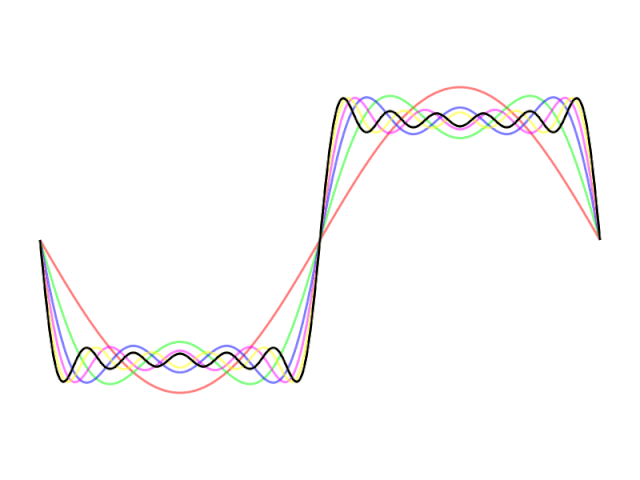
Простыми словами, мы хотим из кучи простых штук воссоздать все что угодно. Например, можно комбинировать и суммировать синусоидальные волны для аппроксимации любой функции.

Как насчет ступенчатой функции?

qk1zz1cwdddh7c78v0xbn782ydy.gif


Код 
using Javis, Colors
function ground(args...)
    background("black")
    sethue("white")
    translate(-args[1].width/2+50, 0)
    scale(700, 150)
end

function wave(xs, ys, opacity, color)
    setline(1.5)
    setopacity(opacity)
    sethue(color)
    points = Vector{Point}(undef, length(xs))
    for (x, y, i) in zip(xs, ys, 1:length(xs))
        points[i] = Point(x, y)
    end
    prettypoly(points, :stroke, ()->())
end

function term(x, i)
    return 4/π * sin.(2π*(2i-1)*x)/(2i-1)
end

function sum_term(x, k)
    k == 0 && return zeros(length(x))
    return sum(term(x, i) for i in 1:k)
end

nframes = 300
frames_per_wave = 40
video = Video(800, 600)
Background(1:nframes, ground)

x = 0.0:0.001:1.0
k = 6
colors = [RGB(0.0, 1.0, 0.4), RGB(0, 1.0, 1.0), RGB(1.0, 0.25, 0.25), 
RGB(1.0, 1.0, 0.0), RGB(1.0, 0.5, 1.0), RGB(0.75, 0.75, 1.0)]
waves = Object[]
for i = 1:k
    frames = frames_per_wave*(i-1)+1:nframes
    push!(waves, Object(frames, (args...; y=term(x,i)) -> wave(x, y, 0.5, colors[i])))
    act!(waves[end], Action(5:frames_per_wave,
                    change(:y, term(x,i) => sum_term(x, i))))
end

sum_wave = Object(1:nframes, (args...; y=zeros(length(x)))->wave(x, y, 1.0, "white"))
for i = 1:k
    act!(sum_wave, Action(frames_per_wave*(i-1)+1:frames_per_wave*i,
                         change(:y, sum_term(x, i-1) => sum_term(x, i))))
end

render(video; pathname="images/fourier_1D.gif")

Мы, в основном, пытаемся объединить простые функции (синусоидальные волны) путем их сложения, чтобы создать квадратную волну.

Важно отметить, что в квадратной функции нет ничего особенного. Подход обобщается на любой пример. Просто нужно насуммировать довольно много функций. Для идеального результата — бесконечно много.


А теперь, бегом в 2D

На самом деле, хочется нарисовать что-то в 2D — это гораздо интереснее. Кстати, вся эта идея использования Javis для визуализации рядов Фурье пришла от Риккардо Чиоффи, которого я люблю называть первым пользователем Javis. Он сам реализовал идею, без нашего ведома, пока мы не увидели его пост об этом на JuliaLang-дискурсе. Посмотрите, пожалуйста!

Имплементация была на предыдущей версии Javis, поэтому код больше не работает. Я подожду здесь пару минут, пока вы будете наслаждаться его потрясающей визуализацией.

Давайте начнем с некоторых строительных блоков, которые имеют смысл для понимания рядов Фурье в 2D. Я начну с кругов и комплексных чисел.

В общем, я пройдусь по тому материалу, который Грант Сандерсон прекрасно объяснил на своем YouTube-канале 3blue1brown Что такое ряды Фурье?. В конце этого поста есть еще несколько ссылок

Мы уже немного покатали круги, но давайте посмотрим, как работать с ними, используя комплексные числа. Я здесь имею в виду использование формулы

$ e^{2\pi i t} $

где t — наша переменная в диапазоне от 0 до 1, а i — мнимая единица.

Таким образом, эта формула дает комплексное число для некоторого t. Мы можем его визуализировать, просто откладывая действительную компоненту нашего комплексного числа на оси x и комплексную компоненту на оси y.

В этой визуализации круг рисуется до определенной точки в каждом кадре и завершает круг с t=1.00

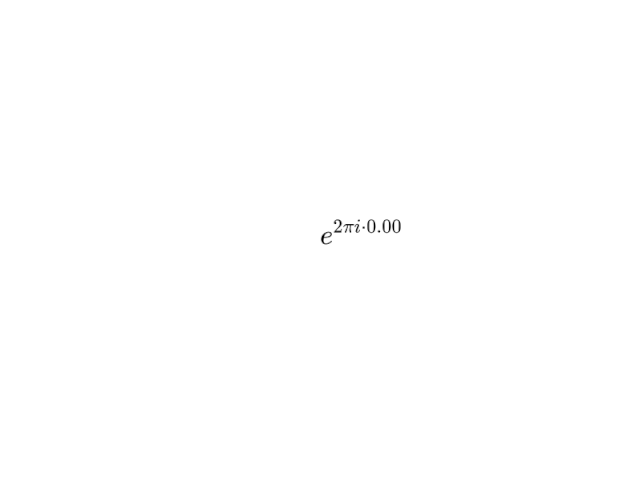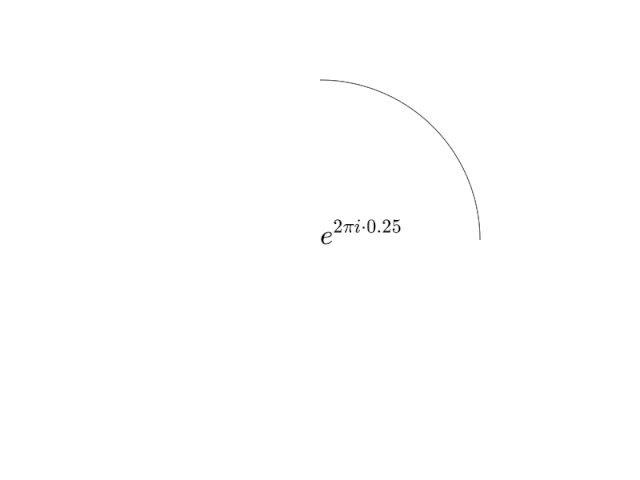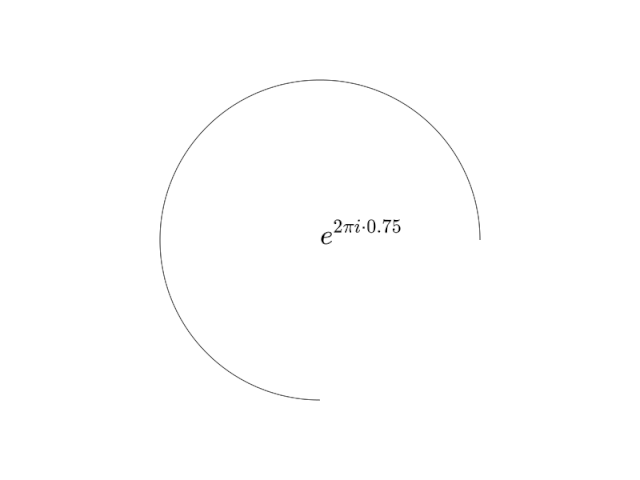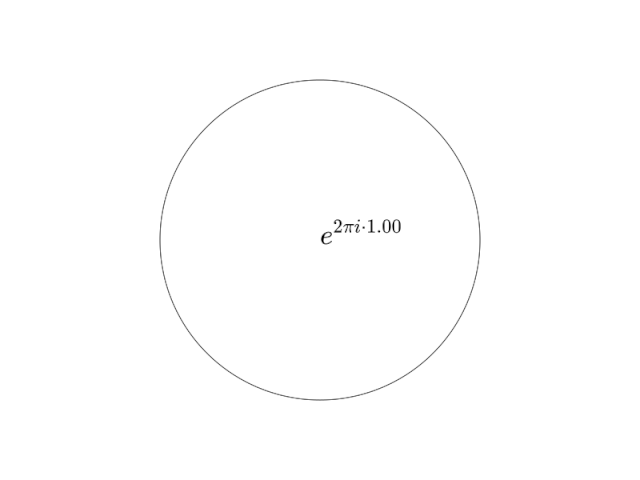
4sbx1wncv02ckifehy9uofwwtyu.gif

Картинку нужно попридержать в уме до конца поста.

Далее мы начнем с некого многоугольника, который мы хотим нарисовать используя круги, вращающиеся вокруг кругов, поскольку круги — это синусоидальные волны двумерного пространства.

Я думаю, что это лучше всего объяснить визуально, поэтому я покажу вам, чего мы пытаемся достичь, а затем покажу, как этого достичь.


Что мы хотим воссоздать

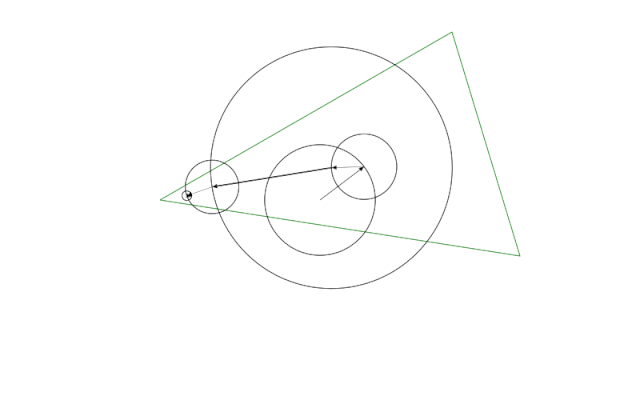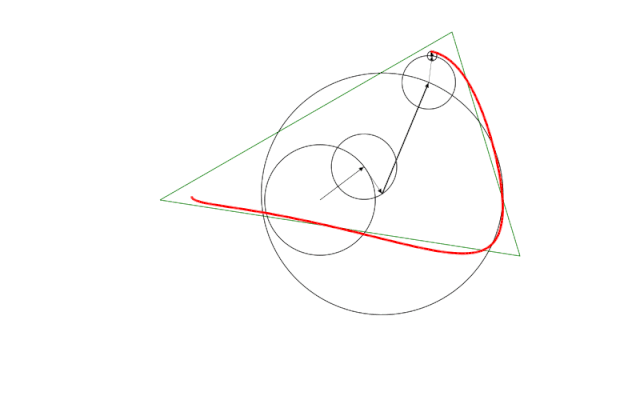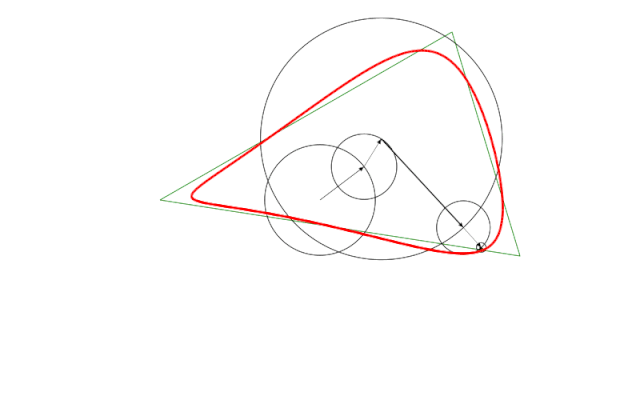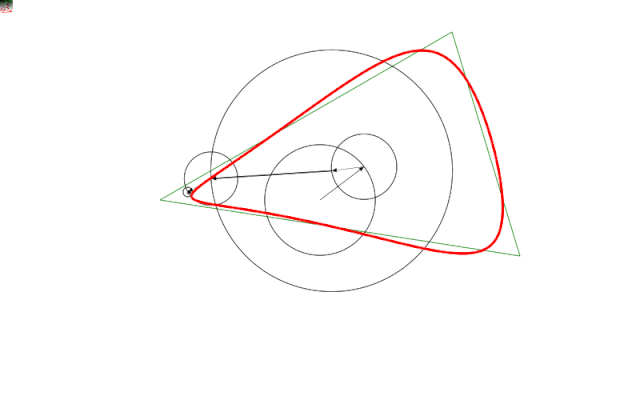
Вот своего рода то, чего мы хотим достичь, но позже мы рассмотрим более сложные формы. Для этого мы будем использовать больше кругов, хоть тогда и труднее понять, что происходит.

zs6vsrvvrgltzhwowam0nx5dbaq.gif


Код 
using Javis, FFTW, FFTViews

function ground(args...)
    background("black")
    sethue("white")
end

function circ(; r = 10, vec = O, action = :stroke, color = "white")
    sethue(color)
    circle(O, r, action)
    my_arrow(O, vec)
    return vec
end

function my_arrow(start_pos, end_pos)
    start_pos ≈ end_pos && return end_pos
    arrow(
        start_pos,
        end_pos;
        linewidth = distance(start_pos, end_pos) / 100,
        arrowheadlength = 7,
    )
    return end_pos
end

function draw_line(
    p1 = O,
    p2 = O;
    color = "white",
    action = :stroke,
    edge = "solid",
    linewidth = 3,
)
    sethue(color)
    setdash(edge)
    setline(linewidth)
    line(p1, p2, action)
end

function draw_path!(path, pos, color)
    sethue(color)

    push!(path, pos)
    draw_line.(path[2:end], path[1:(end - 1)]; color = color)
end

function get_points(npoints, options)
    Drawing()
    shape = poly([Point(-200, 0), Point(250, 70), Point(165, -210)]; close=true)
    points = [Javis.get_polypoint_at(shape, i / (npoints-1)) for i in 0:(npoints-1)]
    return points
end

function poly_color(points, action; color=nothing)
    color !== nothing && sethue(color)
    poly(points, action)
end

c2p(c::Complex) = Point(real(c), imag(c))

remap_idx(i::Int) = (-1)^i * floor(Int, i / 2)
remap_inv(n::Int) = 2n * sign(n) - 1 * (n > 0)

function animate_fourier(options)
    npoints = options.npoints
    nplay_frames = options.nplay_frames
    nruns = options.nruns
    nframes = nplay_frames + options.nend_frames

    points = get_points(npoints, options)
    npoints = length(points)
    println("#points: $npoints")

    # optain the fft result and scale
    x = [p.x for p in points]
    y = [p.y for p in points]

    fs = fft(complex.(x, y)) |> FFTView
    # normalize the points as fft doesn't normalize
    fs ./= npoints
    npoints = length(fs)

    video = Video(options.width, options.height)
    Background(1:nframes, ground)
    Object((args...)->poly_color(points, :stroke; color="green"))

    circles = Object[]
    npoints = 5

    for i in 1:npoints
        ridx = remap_idx(i)

        push!(circles, Object((args...) -> circ(; r = abs(fs[ridx]), vec = c2p(fs[ridx]))))

        if i > 1
            # translate to the tip of the vector of the previous circle
            act!(circles[i], Action(1:1, anim_translate(circles[i - 1])))
        end
        ridx = remap_idx(i)
        act!(circles[i], Action(1:nplay_frames, anim_rotate(0.0, ridx * 2π * nruns)))
    end

    trace_points = Point[]
    Object(1:nframes, (args...) -> draw_path!(trace_points, pos(circles[end]), "red"))

    render(video, pathname = options.filename)
end

function main()
    gif_options = (
        npoints = 1000, # rough number of points for the shape => number of circles
        nplay_frames = 400, # number of frames for the animation of fourier
        nruns = 2, # how often it's drawn
        nend_frames = 0,  # number of frames in the end
        width = 800,
        height = 500,
        shape_scale = 0.8, # scale factor for the logo
        tsp_quality_factor = 40,
        filename = "images/fourier_tri_5.gif",
    )
    animate_fourier(gif_options)
end

main()

Здесь мы попытаемся нарисовать зеленый треугольник, используя пять кругов. Они аппроксимируют треугольник, как вы можете видеть, красной фигурой. У каждого круга имеется прикрепленный к нему вектор. Начнем с внутренней неподвижной окружности, где вектор фиксирован.

Вектор указывает на центр треугольника, что имеет смысл, поскольку это лучшая точка, чтобы убедиться, что баланс вращающихся вокруг нее кругов не нарушен. Я также вернусь к этому позже в этом длинном-длинном посте.

Как насчет следующего круга в цепочке? Он не движется, но его центр находится там, куда указывал последний круг. Кроме того, вектор внутри теперь вращается. Один полный оборот по часовой стрелке эквивалентен одному проходу по контуру рисунка.


Вы могли бы задаться вопросом, почему это по часовой стрелке, а не против? Это связано с тем, что ось y положительна вниз и отрицательна вверх. Впрочем, это не имеет значения.

А вот следующие три круга двигаются. Вектор внутри каждого последующего в цепочке имеет ту же скорость, что и предыдущий круг, но работает против часовой стрелки. Два других делают два полных круга за один проход по рисунку. Один идет по часовой стрелке, другой — против.

Это вроде как все, что нужно. Ну, по крайней мере, это дает визуализацию того, чего мы хотим достичь, и вы уже можете догадаться, что добавление большего количества кругов делает приближение лучше.


Как это посчитать

В этом разделе я хочу немного поговорить о формуле, которую некоторые из вас, возможно, видели раньше, и вычислить параметры пяти кругов, показанных выше.

$ \sum_{k=-n}^n c_k e^{k\cdot 2\pi i t} $

Мы уже видели $e^{2\pi i t}$ раньше, так что k — это единственная новая вещь в экспоненциальной части. Из анимации круга выше видно, что k в основном, просто определяет скорость, а знак k — направление вращения.

Это означает, что у нас есть невращающийся круг с k=0 и вращающиеся круги с $k \in \{-1, 1, -2, 2\}$. Единственное, что осталось, — это $c_k$.

$c_k$ определяет радиус круга, например, 2.5 или 0.5. Кроме того, они задают начальное вращение круга. Это показывается с помощью внутреннего вектора. Мы уже немного посмотрели на комплексные числа, и при определении $c_k$ как комплексного числа у нас есть необходимые два компонента, заданные абсолютным значением и углом комплексного числа.


Такое объяснение отлично от того, что Вы можете найти на других сайтах, поскольку есть разные способы выражения данной концепции. Моя версия эквивалентна тому, как Грант Сандерсон объяснил это в своем видео Что такое ряды Фурье?.

Давайте посмотрим на компоненты для n=1:

$ c_{-1} e^{-2\pi i t} + c_{0} e^{0\cdot 2\pi i t} + c_{1} e^{2\pi i t} $

что может быть упрощено с помощью $e^0 = 1$:

$ c_{-1} e^{-2\pi i t} + c_{0} + c_{1} e^{2\pi i t} $

Что произойдет, если мы возьмем среднее значение этого показателя, когда позволим t перейти от 0 к 1 и нарисуем полные круги?

Прежде всего, мы можем вычислить среднее значение суммы, суммируя средние значения.

Если мы усредним положения окружности, то получим центр, который находится в точке (0,0) для всех из них. Поэтому усреднение по всем возможным t между 0 и 1 (или, по крайней мере, хорошее подмножество всех возможностей… хорошо, скажем, несколько сотен значений вместо бесконечного множества)
мы получаем $c_0$. Чудненько, да?

Давайте повторим это еще раз: мы усредняем по слагаемым, и поскольку все слагаемые, кроме $c_0$, являются кругами, они усредняются до $(0, 0)$ и не имеют отношения к делу.

Это была также интуиция, которую мы получили из результата, показанного с пятью кругами, отчаянно пытающимися приблизиться к треугольнику.

Ну подождите, а как мы получим $c_{-1}$ и все остальные константы $c_k$?

На самом деле мы делаем точно то же самое и просто умножаем все уравнение на $e^{1\cdot 2\pi i t}$, чтобы получить сдвинутую версию. Помните, что $e^x \cdot e^y = e^{x+y}$ такое, что мы можем отменить показатель степени с помощью этого умножения. Умножая на $e^{1\cdot 2\pi i t}$, мы вычеркиваем компонент, который у нас есть для $k=-1$. Мы можем сделать то же самое для всех констант.

Давайте сделаем хорошую визуализацию для этого:

zubars0em9g-zlmk3hxboyz8z0i.gif

Немного сложно для восприятия, так что остановимся поподробней:


  1. Начнем с зеленого треугольника
  2. Выбираем 100 точек на этом треугольнике и усредняем его
  3. Создаем окружность с центром в начале координат и указываем на среднее значение с помощью вектора
  4. Умножаем треугольник на $e^{k \cdot 2\pi i t}$ с $k=-1$ и t зависящим от положения, в котором мы находимся на треугольнике.
  5. Создаем новые 100 точек и снова усредняем их
  6. Создаем новый круг
  7. Перемещаем вновь созданный круг на вершину предыдущего круга

И так повторяем, чтобы получить все остальные константы и, следовательно, круги, которые нам нужно добавить.


Работать сподручней с пакетами

Вместо того чтобы умножать и усреднять собственноручно, мы можем использовать для этого пакет. Я надеюсь, что смогу убедить всех, кто не был убежден раньше, что ряды Фурье это прекрасно, и конечно, с ними связано гораздо больше крутых штук, чем я объяснил здесь или понял сам

Есть два хороших пакета, которые я использовал в своей анимации треугольника Фурье показанном раньше:

Первый из них выполняет тяжелые вычисления, и делает это быстро, поэтому первая буква «F» в названии означает «быстрый».

С другой стороны, FFTViews просто облегчает работу. Как вы уже видели, мы имеем дело с отрицательными и положительными значениями для k.

FFTW создает вектор со всеми этими константами $c_k$, но FFTViews позволяет индексировать эту информацию более естественно, например так c[-3], даже несмотря на то, что Julia — это язык, с индексацией начинающейся с единицы.

А потом вводится вектор точек как вектор комплексных чисел. Дополнительный шаг, который нужно выполнить, — это усреднить результат, поскольку это не делается алгоритмом (вероятно, это будет один из способов сделать его быстрее)

Под средним я подразумеваю, что нужно разделить результат на количество точек.

Я хотел бы закрыть этот пост, показав окончательный результат и немного того, что было необходимо для этого. После этого я, как обычно, выложу ссылку на код.


The final animation

dlajobo-jfq0rcwizll94yqza5q.gif

В этом примере я также использовал задачу коммивояжера (TSP), чтобы объединить все буквы в одну непрерывную форму.


Короткая заметка:
Если вас интересует проблема коммивояжера или оптимизация в целом я настоятельно рекомендую проверить мои ранние посты:

Ладно вернемся к посту:

Нам нужно использовать задачу коммивояжера, чтобы избежать больших скачков от одной буквы к другой, поскольку рисунок непрерывен. Потенциально можно избавиться от всех скачков вместе, имея версию ряда Фурье с разрывом.

В коде, который я прикрепил ниже, я также использую одну переменную для количества точек и кругов, что не самая лучшая идея, и я изменил ее для рисования треугольника, но в этом случае я хотел ограничить время работы эвристического решателя TSP.


Выводы

Прежде чем я закончу этот пост рекламой для себя, позвольте мне немного подытожить то, что мы узнали за последние 20 минут.


  1. Основные изменения в Javis v0.3
  2. Рисование простых фигур и применение к ним действий
  3. Что можно сделать с рядами Фурье в 1D и 2D
  4. Формула и объяснение ряда Фурье
  5. Интуиция, как получить необходимые константы


Ссылки

Далее идут ссылочки на реквизиты и персональные благодарности за патронаж, так что не скупимся и поддерживаем товарища Оле Крюгера ведущего интересный блог.

© Habrahabr.ru