[Перевод] Индексируем миллиарды текстовых векторов

При извлечении информации часто возникает задача поиска подобных фрагментов текста. В контексте поиска запрос может быть сгенерирован пользователем (например, текст, который пользователь вводит в поисковом движке) или самой системой. Часто нам нужно сопоставлять входящий запрос с уже проиндексированными запросами. В этой статье мы рассмотрим, как можно построить систему, решающую эту задачу применительно к миллиардам запросов без траты целого состояния на серверную инфраструктуру.
Сначала формально определим задачу:
Дан фиксированный набор запросов, входящий запрос
и целое число
. Нужно найти такое подмножество запросов
, чтобы каждый запрос
был более подобен
, чем какой-либо иной запрос в
.
Например, при таком наборе запросов :
{tesla cybertruck, beginner bicycle gear, eggplant dishes, tesla new car, how expensive is cybertruck, vegetarian food, shimano 105 vs ultegra, building a carbon bike, zucchini recipes}
и можно ожидать такой результат:
Обратите внимание, что мы ещё не определили критерий подобия. В этом контексте это может означать практически всё, что угодно, но обычно сводится к некой форме подобия на основе ключевых слов или векторов. С помощью подобия на основе ключевых слов мы можем счесть два запроса подобными, если они содержат достаточно общих слов. Например, запросы «opening a restaurant in munich» и «best restaurant of munich» являются подобными, потому что в них есть слова «restaurant» и «munich». А запросы «best restaurant of munich» и «where to eat in munich» уже менее подобны, потому что в них лишь одно общее слово. Однако кому-то из ищущих ресторан в Мюнхене будет лучше, если подобными окажется вторая пара запросов. И в этом нам поможет сопоставление на основе векторов.
Векторное представление слов — это методика машинного обучения, используемая при обработке естественного языка для преобразования текста или слов в векторы. Перенеся задачу в векторное пространство, мы можем использовать математические операции с векторами — суммирование и вычисление расстояний. Для установления связей между подобными словами можно использовать традиционные методы векторной кластеризации. Значение этих операций в исходном пространстве слов может быть неочевидным, но преимущество в том, что теперь нам доступен широкий набор математических инструментов. Если вас интересуют подробности о векторах слов и их применении, почитайте про word2vec и GloVe.
У нас есть способ генерирования векторов из слов, теперь соберём их в текстовые векторы (векторы документов или выражений). Проще всего сделать это с помощью сложения (или усреднения) векторов всех слов в тексте.

Иллюстрация 1: Векторы запросов.
Теперь можно определить подобие двух фрагментов текста (или запросов) с помощью их представления в векторном пространстве и вычисления расстояния между векторами. Обычно для этого применяют угловое расстояние.
В итоге, векторное представление слов позволяет выполнять текстовое сопоставление другого типа, которое дополняет сопоставление на основе ключевых слов. Можно исследовать семантическое подобие запросов (например, «best restaurant of munich» и «where to eat in munich») так, как ранее мы сделать не могли.
Теперь мы можем уточнить нашу исходную задачу сопоставления запросов:
Дан фиксированный набор векторов запросов, входящий вектор
и целое число
. Нужно найти такое подмножество векторов
, чтобы угловое расстояние от
до каждого вектора
был меньш растояния до какого-либо иного вектора в
.
Это называется задачей поиска ближайшего соседа. Существует ряд алгоритмов для её быстрого решения в низкоразмерных пространствах. Но при работе с векторными представлениями слов мы обычно оперируем высокоразмерными векторами (100–1000 размерностей). И здесь упомянутые методы уже не работают.
Не существует подходящего способа быстро определить ближайших соседей в высокоразмерных пространствах. Поэтому упростим проблему, допустив использование приблизительных результатов: вместо того, чтобы алгоритм всегда возвращал именно ближайшие векторы, будем довольствоваться только некоторыми из ближайших или в некоторой степени близкими соседями. Это называется задачей приблизительного поиска ближайших соседей и является областью активных исследований.
Иерархический маленький мир
Иерархический маленький мир (Hierarchical Navigable Small-World graph, HNSW) — один из самых быстрых алгоритмов приблизительного поиска ближайших соседей. Поисковый индекс в HNSW представляет собой многоуровневую структуру, в которой каждый уровень является графом близости. Каждый узел графов соответствует одному из векторов запросов.
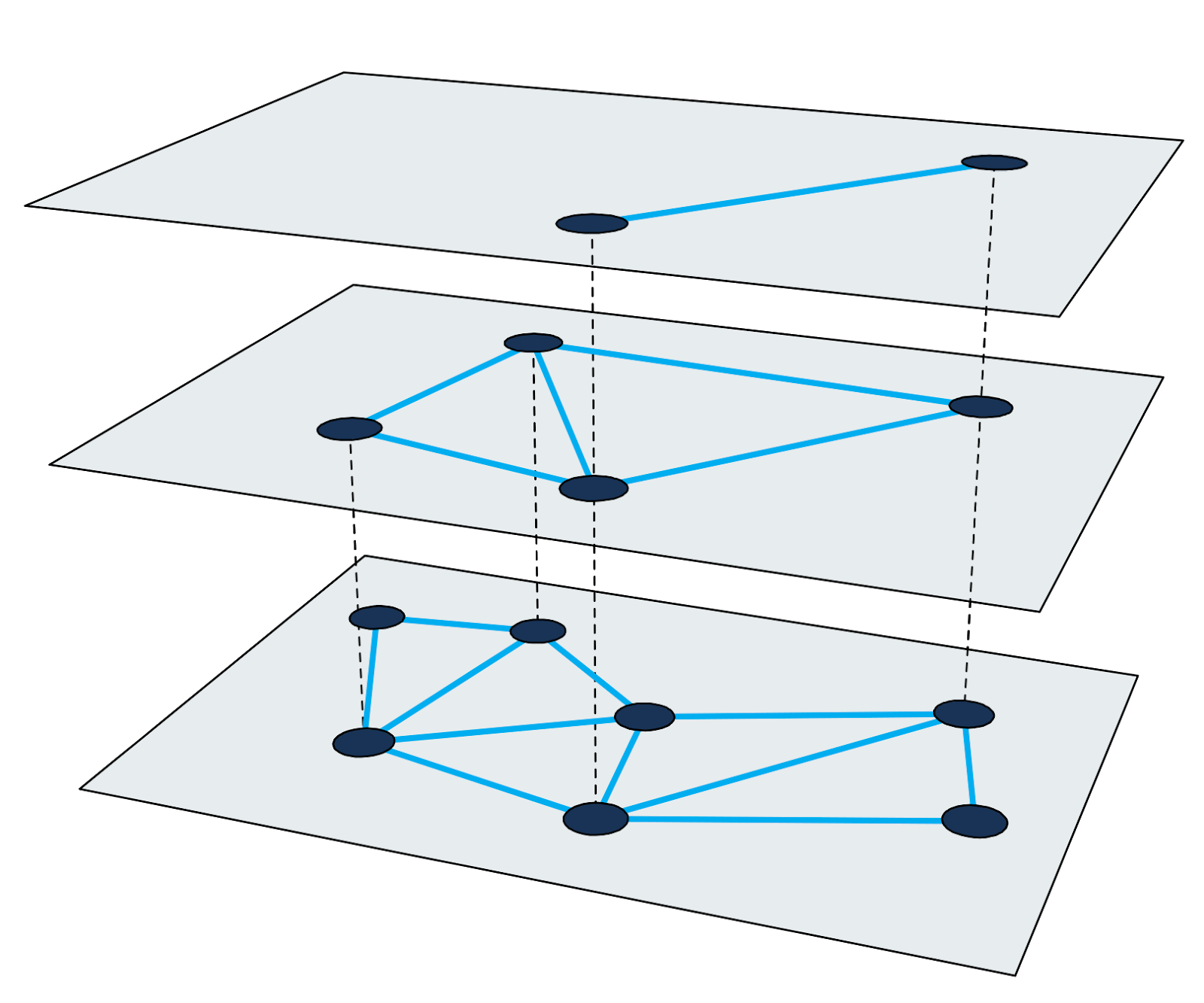
Иллюстрация 2: Многоуровневый граф близости.
Поиск ближайших соседей в HNSW использует метод увеличения (zooming-in). Он начинается во входной ноде самого верхнего уровня и рекурсивно выполняет жадный обход графов на каждом уровне, пока не достигнет локального минимума на самом дне.
Подробности об алгоритме и методике поиска хорошо описаны в научной работе. Важно запомнить, что каждый цикл поиска ближайших соседей состоит из обхода узлов графов с вычислением расстояний между векторами. Ниже мы рассмотрим эти этапы, чтобы использовать данный метод для создания крупномасштабного индекса.
Предположим, что нам нужно проиндексировать 4 миллиарда 200-мерных векторов запросов, причём каждое измерение представлено четырёхбайтным числом с плавающей запятой (4 млрд — это достаточно много, чтобы задача оказалась интересной, но при этом ещё можно было хранить ID узлов в обычных четырёхбайтных числах). Примерный подсчёт говорит нам, что размер одних лишь векторов составит около 3 ТБ. Поскольку большинство существующих библиотек для приблизительного поиска ближайших соседей используют ёмкость оперативной памяти, нам понадобится очень большой сервер, чтобы запихнуть в RAM хотя бы векторы. Обратите внимание, что здесь не учтён дополнительный поисковый индекс, который необходим для большинства методов.
За всю историю развития нашего поискового движка мы использовали несколько разных подходов для решения этой проблемы. Рассмотрим некоторые из них.
Подмножество данных
Первый и самый простой подход, который не позволил нам полностью решить проблему, заключался в ограничении количества векторов в индексе. Взяв одну десятую данных, мы создали индекс, которому требуется — сюрприз — 10% памяти. Однако качество поиска ухудшилось, поскольку теперь мы оперировали меньшим количеством запросов.
Квантование
Здесь мы использовали все данные, но уменьшили их с помощью квантования (применяли разные методики квантования, например, product quantization, но не смогли добиться нужного качества работы при таком объёме данных). Округлив некоторые ошибки, мы смогли заменить все четырёхбайтные числа в исходных векторах на квантованные однобайтные версии. Объём оперативной памяти под векторы уменьшился на 75%. Однако нам всё ещё требовалось 750 Гбайт памяти (не считая размера самого индекса), а это по прежнему очень большой сервер.
У описанных подходов были свои достоинства, но они требовали много ресурсов и давали плохое качество поиска. Хотя есть библиотеки, дающие отклик менее, чем за 1 мс, однако мы могли пожертвовать скоростью в обмен на уменьшение требований к оборудованию.
Granne (graph-based approximate nearest neighbors) — это HNSW-библиотека, разработанная и использованная в Cliqz для поиска подобных запросов. У неё открытый исходный код, однако библиотека пока ещё активно разрабатывается. Улучшенная версия будет опубликована на crates.io в 2020-м. Она написана на Rust со вставками на Python, предназначена для обработки миллиардов векторов с применением конкурентности. С точки зрения векторов запросов интересно то, что в Granne есть особый режим, требующий гораздо меньше памяти по сравнению с другими библиотеками.
Компактное представление векторов запросов
Уменьшение размера векторов запросов даст нам много выгод. Для этого давайте вернёмся назад и рассмотрим создание векторов. Поскольку запросы состоят из слов, а векторы запросов являются суммами векторов слов, мы можем явно отказаться от хранения векторов запросов и вычислять их по мере необходимости.
Можно хранить запросы в виде наборов слов и использовать поисковую таблицу для нахождения соответствующих векторов. Однако мы избегаем перенаправления, сохраняя каждый запрос в виде списка целочисленных ID, соответствующих векторам слов в запросе. Например, сохраним запрос «best restaurant of munich» как , где
— это ID вектора слова «best», и т. д. Допустим, у нас меньше 16 млн векторов слов (больше этого количества обойдётся по 1 байту за слово), тогда можно использовать по 3 байта для представления всех ID слов. То есть вместо хранения 800 байтов (или 200 байтов в случае квантованных векторов) мы будем хранить для этого запроса лишь 12 байтов (Это не совсем так. Поскольку запросы состоят из разного количества слов, нам нужно хранить ещё и смещение списка в индексе слов. Для этого понадобится по 5 байтов на запрос).
Что касается векторов слов, то они всё нужны нам. Однако количество слов гораздо меньше количество запросов, которые можно создать, комбинируя эти слова. А значит и размер слов не так важен. Если хранить векторы слов в виде четырёхбайтных версий с плавающей запятой в простом массиве , то нам понадобится меньше 1 Гбайт на каждый миллион слов. Этот объём легко поместится в оперативную память. Теперь вектор запроса выглядит так:
.
Финальный размер представления запроса зависит от общего количества слов в запросе. Для 4 млрд запросов это около 80 Гбайт (включая векторы слов). Иными словами, по сравнению с исходными векторами слов размер уменьшился на 97%, а по сравнению с квантованными векторами — на 90%.
И ещё кое-что. Для одного поиска нам нужно посетить примерно 200–300 узлов графа. Каждый узел имеет 20–30 соседей. Значит, нам нужно вычислить расстояние от входного вектора запроса до 4000–9000 векторов в индексе. И более того, нам нужно сгенерировать векторы. Сколько времени займёт создание векторов запросов на лету?
Оказывается, с достаточно новым процессором эта задача решается за несколько миллисекунд. Запрос, который раньше выполнялся за 1 мс, теперь выполняется примерно за 5 мс. Но зато мы уменьшили объём памяти под векторы на 90%. Мы с радостью приняли такой компромисс.
Отображение в памяти векторов и индекса
Выше мы решали задачу уменьшения объёмов памяти под векторы. Но после того, как мы решили эту задачу, ограничивающим фактором стала сама структура индекса. Теперь нужно уменьшить и её размер.
В Granne графовая структура компактно хранится в виде списков смежностей (adjacency list) с переменным количеством соседей у каждой ноды. То есть на метаданные память почти не тратится. Размер структуры индекса во многом зависит от параметров конструирования и свойств графа. Тем не менее, чтобы получить представление о размере индекса, достаточно сказать, что мы можем построить индекс для 4 млрд векторов общим размером около 240 Гбайт. Это может быть допустимо для in-memory-использования на большом сервере, но можно сделать лучше.
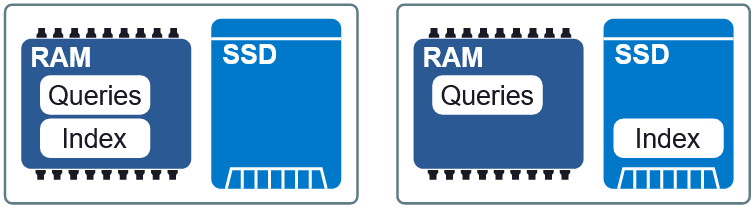
Иллюстрация 3: Две разные схемы размещения в RAM и SSD.
Важным свойством Granne является возможность отображать в памяти индекс и векторы запросов. Это позволяет нам лениво загружать индекс и совместно использовать память несколькими процессами. Индекс и файлы запросов разбиваются на отдельные файлы отображения в памяти и могут использоваться в разных схемах размещения в оперативной памяти и на SSD. Если требования к задержке чуть ниже, то пометив индекс на SSD, запросы в оперативную память, мы сохраняем приемлемую скорость без избыточного потребления памяти. В конце статьи мы увидим, как выглядит этот компромисс.
Улучшение локальности данных
В нашей текущей конфигурации, когда индекс находится на SSD, каждый запрос требует до 200–300 чтений с диска. Можно попробовать увеличить локальность данных, упорядочив элементы, чьи векторы настолько близки, что их HNSW-узлы расположены в индексе тоже неподалёку друг от друга. Локальность данных улучшает производительность, потому что в одной операции чтения (обычно извлекается от 4 Кб) с большей вероятностью содержатся и другие узлы, необходимые для обхода графа. А это, в свою очередь, уменьшает количество извлечений данных в ход одного поиска.

Иллюстрация 4: Локальность данных снижает количество извлечений информации.
Нужно отметить, что переупорядочивание элементов не влияет на результаты поиска, это способ его ускорения. То есть порядок может быть любым, но не всякий вариант ускорит поиск. Очень трудно найти оптимальный порядок. Однако эвристика, которую мы успешно использовали, заключается в сортировке запросов по самому важному слову в каждом запросе.
Мы используем Granne для создания и сопровождения многомиллиардных индексов с векторами запросов, чтобы искать подобные запросы с относительно небольшим потреблением памяти. В таблице ниже представлены требования в рамках разных методов. Скептически отнеситесь к абсолютным значениям задержек в ходе поиска, потому что они сильно зависят от того, что считается приемлемым откликом. Однако эта информация описывает относительную производительность методов.
* Выделение индексу памяти больше требуемого объёма привело к кэшированию некоторых узлов (часто посещаемых), что уменьшило задержку при поиске. Для этого не использовался внутренний кэш, только внутренние средства ОС (ядро Linux).
Нужно отметить, что некоторые упомянутые в статье оптимизации неприменимы для решения общей задачи поиска ближайших соседей с неразложимыми векторами. Однако они применимы в любых ситуациях, когда элементы могут генерироваться из меньшего количества частей (как в случае со словами и запросами). В противном случае всё ещё можно использовать Granne с исходными векторами, просто потребуется больше памяти, как с другими библиотеками.
