[Перевод] Имитация рисования от руки на примере RoughJS04.05.2020 08:38

RoughJS это маленькая (эскизном, рукописном стиле. Она позволяет рисовать на и с помощью SVG. В этом посте я хочу ответить на самый популярный вопрос о RoughJS: как это работает?

Немного истории

Очарованный изображениями рукописных графиков, схем и эскизов, я, как истинный нерд, задался вопросом: можно ли создавать такие рисунки с помощью кода, как можно точнее имитировать рисунок от руки, в то же время сохранив возможность программной реализации? Я решил сосредоточиться на примитивах — линиях, многоугольниках, эллипсах и кривых, чтобы создать целую библиотеку 2D-графики. На её основе можно создавать библиотеки и графики для рисования графиков и схем.

Вкратце изучив вопрос, я нашёл статью Джо Вуда и его коллег под названием Sketchy rendering for information visualization. Описанные в ней техники стали основой библиотеки, особенно в рисовании линий и эллипсов.

В 2017 году я написал первую версию библиотеки, которая работала только на Canvas. Решив задачу, я потерял к ней интерес. Год спустя я много работал с SVG, и решил адаптировать RoughJS для работы с SVG. Также я изменил структуру API, сделав её более простой, и сосредоточился на простых векторных графических примитивах. Я рассказал о версии 2.0 на Hacker News и внезапно она обрела огромную популярность. В 2018 году это был второй по популярности пост ShowHN.
С тех пор другие люди создали на основе RoughJS более удивительные вещи, например, Excalidraw, Why do Cats & Dogs…, библиотеку графиков roughViz.

А теперь давайте поговорим об алгоритмах…

Неровность

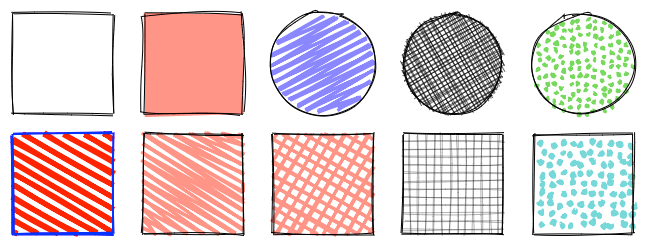
Фундаментальной основой имитации рукописных фигур является случайность. Когда мы рисуем вручную, любые две фигуры будут чем-то отличаться. Никто не рисует идеально точно, поэтому каждая пространственная точка в RoughJS корректируется на случайное смещение. Величина случайности задаётся числовым параметром roughness.

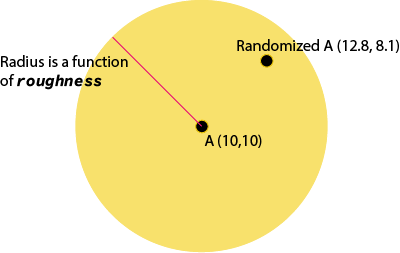
Представим точку A и окружность вокруг неё. Теперь заменим A случайной точкой в пределах этой окружности. Площадью этой окружности случайности управляет значение roughness.

Линии

Рукописные линии никогда не бывают прямыми и часто в них проявляется кривизна изгиба (описанная здесь). Мы рандомизируем две конечные точки отрезка на основании roughness. Затем выберем ещё две случайные точки примерно на расстоянии 50% и 75% от конца отрезка. Соединив эти точки кривой, мы получим эффект изгиба.

При рисовании вручную люди иногда двигают карандашом вперёд и назад по линии. Это нужно или для того, чтобы сделать линию более яркой, или просто для исправления прямоты линии. Выглядит это примерно так:

Чтобы добавить эффект эскизности, RoughJS рисует линию дважды. В будущем я планирую сделать этот аспект более настраиваемым.

Посмотрите на эту поверхность canvas. Параметр roughness изменяет внешний вид линий:

В оригинале статьи на canvas можно порисовать самостоятельно.

При рисовании вручную длинные линии обычно становятся менее прямыми и более кривыми. То есть случайность смещений для создания эффекта изгиба является функцией от длины линии и значения randomness. Однако для очень длинных линий масштабирование этой функции не подходит. Например, на показанном ниже изображении концентрические квадраты нарисованы с одинаковыми случайными seed, т.е. по сути они являются одной случайной фигурой, но с разным масштабом.

Можно заметить, что края внешних квадратов выглядят немного более неровными, чем у внутренних. Поэтому я также добавил коэффициент затухания, зависящий от длины линии. Коэффициент затухания применяется как ступенчатая функция при различных длинах.

Эллипсы (и окружности)

Возьмите лист бумаги и одним непрерывным движением нарисуйте как можно быстрее несколько кругов. Вот что получилось у меня:

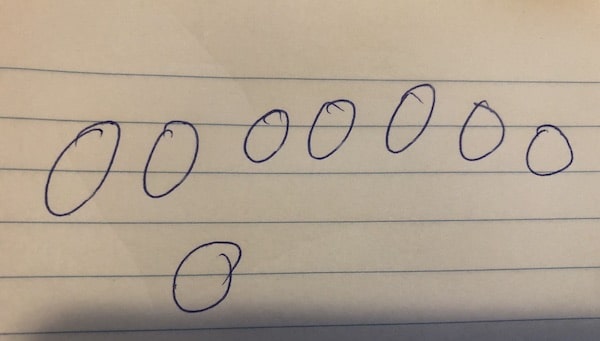
Заметьте, что начальная и конечная точки петли не всегда совпадают. RoughJS пытается имитировать это, делая при этом внешний вид более завершённым (техника адаптирована из статьи giCenter).

Алгоритм находит n точек эллипса, где n определяется размером эллипса. Затем каждая точка рандомизируется на величину его roughness. Далее через эти точки проводится кривая. Чтобы получить эффект раъединённых концов точки со второй по последнюю не совпадают с первой точкой. Вместо этого кривая соединяет вторую и третью точки.

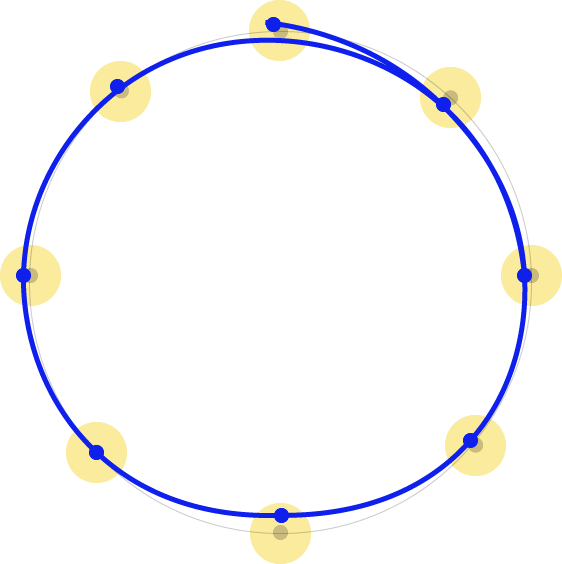
Также рисуется второй эллипс, чтобы петля была более замкнутой и обладала дополнительным эффектом эскиза.

В оригинале статьи можно рисовать эллипсы на интерактивной поверхности canvas. Изменяйте roughness и наблюдайте, как меняется форма:

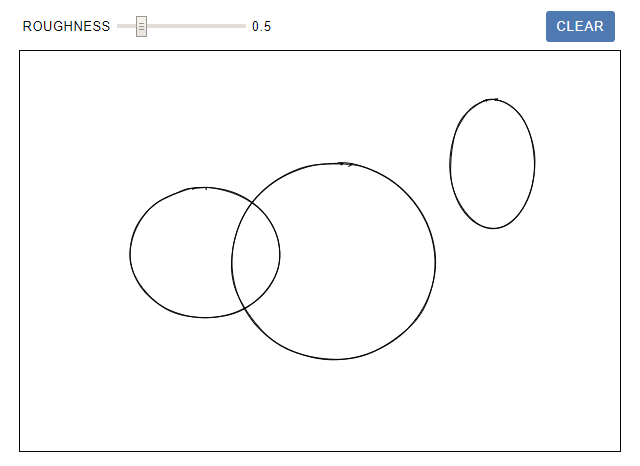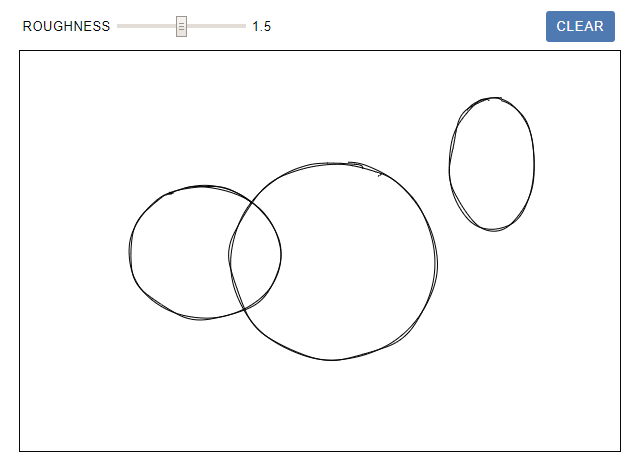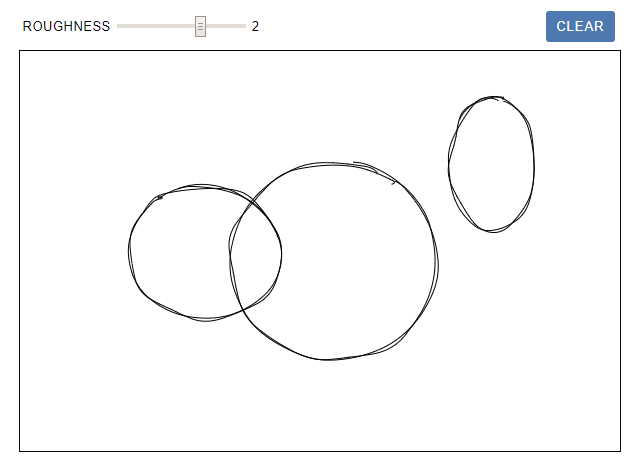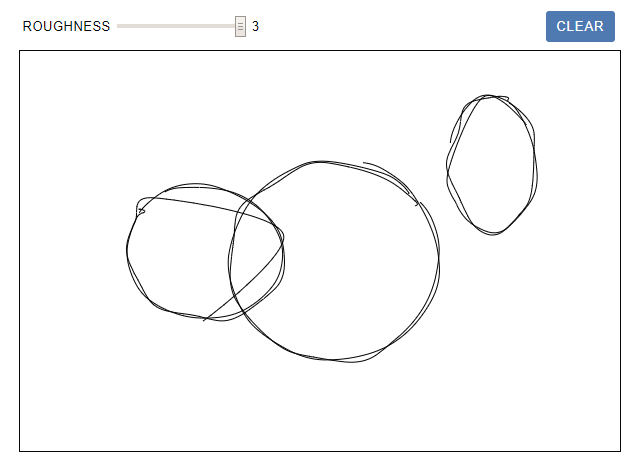
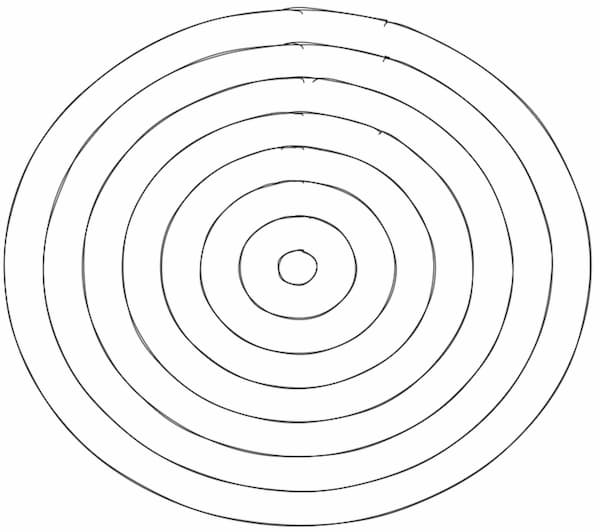
В случае рисования линий некоторые из этих артефактов становятся более акцентированными, если какая-то фигура масштабируется до разных размеров. В эллипсе этот эффект более заметен, потому что соотношение является квадратичным. На показанном ниже изображении все круги имеют одинаковую форму, но внешние выглядят более неровными.

Алгоритм выполняет автоматическую настройку на основании размера фигуры, увеличивая количество точек в круге (n). Ниже показан тот же набор кругов, сгенерированный с использованием автоматической настройки.

Заполнение

Для заполнения нарисованных от руки фигур обычно используются штриховые линии. В случае эскизов от руки линии не всегда остаются в пределах контуров фигур. Они тоже рандомизированы. Плотность, угол, ширину линий можно настраивать.

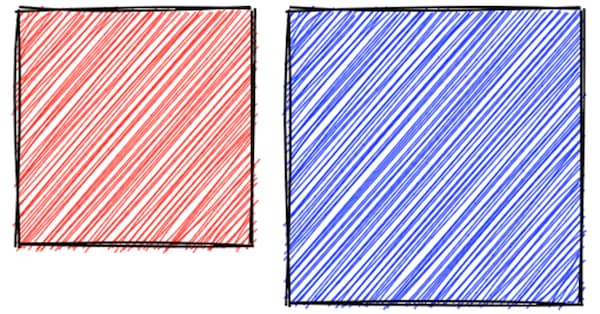
Показанные выше квадраты заполнять легко, но в случае других фигур могут возникать всевозможные проблемы. Например, вогнутые многоугольники (в которых углы могут превышать 180°) часто вызывают такие проблемы:

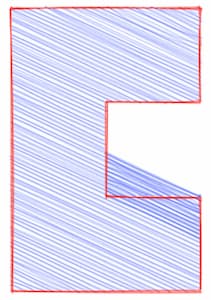
На самом деле показанное выше изображение взято из отчёта об ошибке в одной из предыдущих версий RoughJS. С тех пор я обновил алгоритм заполнения штрихами, адаптировав версию метода сканирования строк.

Алгоритм сканирования строк можно использовать для заполнения любого многоугольника. Его принцип заключается в сканировании многоугольника при помощи горизонтальных строк (растровых строк). Растровые строки идут с верха полигона вниз. Для каждой растровой строки мы определяем, в каких точках строка пересекается с многоугольником. Мы выстраиваем эти точки пересечения слева направо.

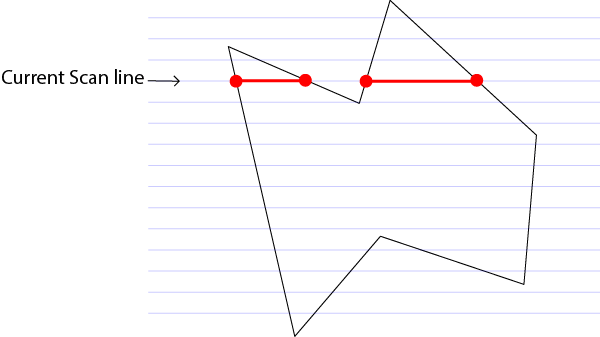
Двигаясь от точки к точке, мы переключаемся из режима заполнения в режим без заполнения; переключение между состояниями происходит при встрече каждой точки пересечения на растровой строке. Здесь нужно учитывать ещё многое, в частности, пограничные случаи и способы оптимизации сканирования; подробнее об этом можно прочитать здесь: Rasterizing polygons, или развернуть спойлер с псевдокодом.

Подробности реализации алгоритма сканирования строк

Мы задаём две структуры данных (таблицы) для хранения данных о рёбрах полигонов.

Первая — это глобальная таблица рёбер (Edge Table, ET), содержащая все рёбра, отсортированные по значению Ymin. Если рёбра имеют одинаковые значения Ymin, то они сортируются по их значению координаты Xmin.

Вторая — это таблица активных рёбер (Active Edge Table, AET), в которой мы храним только те рёбра, которые пересекают текущую растровую строку.

Ниже представлено описание структуры данных в каждой строке таблиц:

interface EdgeTableEntry {
  ymin: number;
  ymax: number;
  x: number; // Initialized to Xmin
  iSlope: number; // Inverse of the slope of the line: 1/m
}

interface ActiveEdgeTableEntry {
  scanlineY: number; // The y value of the scanline
  edge: EdgeTableEntry;
}

После инициализации таблицы рёбер, мы выполняем следующие действия:

1. Присваиваем y значение наименьшего y в ET. Эта переменная обозначает текущую растровую строку.

2. Инициализируем AET как пустую таблицу.

3. Повторяем следующие действия, пока и AET, и ET не опустеют:

(a) Перемещаем из области ET y в AET рёбра, у которых ymin ≤ y.

(b) Удаляем из AET элементы, у которых y = ymax, а затем сортируем AET по x.

(d) Выполняем инкремент y на соответствующее значение, определяемое плотностью штрихов, т.е. на следующую растровую строку.

(e) Для каждого невертикального ребра, оставшегося в AET, обновляем x для нового y (edge.x = edge.x + edge.iSlope)

На изображении ниже (в оригинале статьи интерактивном), каждый квадрат обозначает пиксель. Можно перемещать вершины, чтобы изменять многоугольник и наблюдать, какие пиксели будут заполняться традиционно.

При заполнении штрихами инкремент растровых строк выполняется с шагом, зависящим от заданной плотности линий штрихов, а каждая линия отрисовывается при помощи описанного выше алгоритма.

Однако этот алгоритм предназначен для горизонтальных растровых строк. Чтобы реализовать различные углы штрихов, алгоритм сначала поворачивает саму фигуру на требуемые угол штрихов. Затем вычисляются растровые строки для повёрнутой фигуры. Далее вычисленные линии поворачиваются обратно на угол штрихов в противоположном направлении.

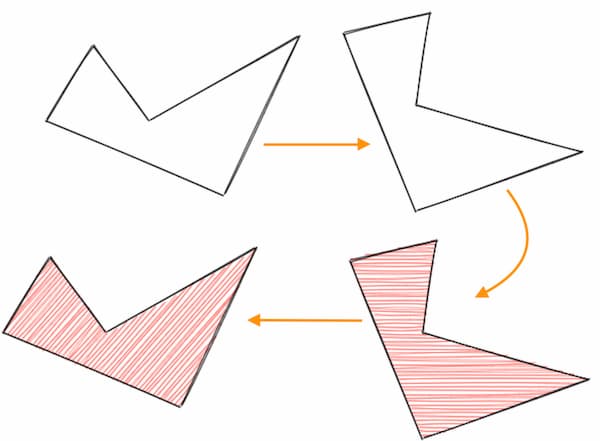
Не только заполнение штрихами

RoughJS поддерживает и другие стили заливки, но все они являются производными от того же алгоритма штрихования. Перекрёстная штриховка заключается в рисовании штриховых линий под углом angle, а затем ещё одних линий под углом angle + 90°. Зигзаг стремится соединить одну штриховую линию с предыдущей. Для получения точечного паттерна нужно отрисовать небольшие круги вдоль штриховых линий.

Кривые

Всё в RoughJS нормализуется до кривых — линии, многоугольники, эллипсы, и т.д. Поэтому естественным развитием этой идеи является создание эскизной кривой. В RoughJS мы передаём кривой множество точек, после чего для их преобразования в кубические кривые Безье используется приближение с помощью кривых.

Каждая кривая Безье имеет две конечные точки и две контрольные точки. Рандомизировав их на основании roughness, можно аналогичным образом создавать «рукописные» кривые.

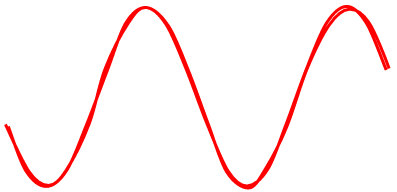
Заполнение кривых

Однако для заполнения кривых требуется обратный процесс. Вместо нормализации всего до кривой, кривая нормализуется до многоугольника. После получения многоугольника можно использовать алгоритм сканирования строк для заполнения искривлённой фигуры.

Сэмплировать точки на кривой с нужной частотой можно при помощи уравнения кубической кривой Безье.

Если использовать частоту сэмплирования, зависящую от плотности штрихов, то мы получим достаточное для заполнения фигуры количество точек. Но это не особо эффективно. Если часть кривой резкая, то нам нужно больше точек. Если часть кривой почти прямая, то потребуется меньше точек. Одним из решений может стать определение кривизны/сглаженности кривой. Если она очень кривая, то мы разделим кривую на две меньшие кривые. Если она сглаженная, то будем рассматривать её просто как прямую.

Сглаженность кривой вычисляется при помощи способа, описанного в этом посте. Значение сглаженности сравнивается со значением допуска, после чего принимается решение, разделять кривую или нет.

Вот та же кривая с уровнем допуска 0,7:

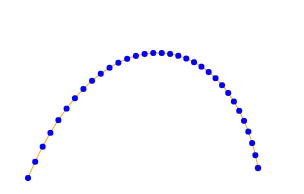
На основании одного только допуска алгоритм обеспечивает достаточное количество точек для представления кривой. Однако он не позволяет эффективным образом избавиться от необязательных точек. В этом поможет второй параметр под названием distance. Для уменьшения количества точек в этом методе используется алгоритм Рамера-Дугласа-Пекера.

Ниже показаны точки, сгенерированные со значениями distance, равными 0.15, 0.75, 1.5 и 3.0.

На основании roughness фигуры можно задать соответствующее значение distance. Получив все вершины многоугольника, мы можем красиво заполнять кривые фигуры:

SVG-контуры

SVG-контуры — это очень мощный инструмент, который можно использовать для создания всевозможных потрясающих изображений, однако из-за этого с ними довольно сложно работать.

RoughJS парсит контур и нормализует его всего на три операции: Move, Line и Cubic Curve. (path-data-parser). После нормализации фигуру можно отрисовывать при помощи описанных выше методик рисования линий и кривых.

Пакет points-on-path объединяет в себе нормализацию контуров и сэмплирование точек кривых для вычисления соответствующих точек контуров.

Ниже представлено примерное вычисление точек для контура M240,100c50,0,0,125,50,100s0,-125,50,-150s175,50,50,100s-175,50,-300,0s0,-125,50,-100s0,125,50,150s0,-100,50,-100:

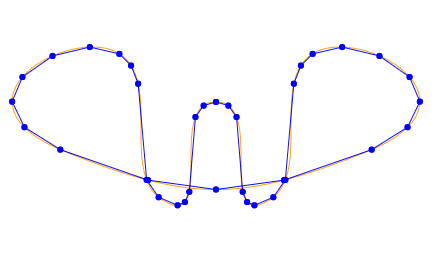
Ещё один пример SVG, который я люблю показывать — эскизная карта Соединённых Штатов:

Попробуйте RoughJS

Зайдите на веб-сайт или в репозиторий на Github или в документацию по API. Подписывайтесь на информацию о проекте в Twitter @RoughLib.