[Перевод] Генератор подземелий на основе узлов графа17.01.2019 11:32

В этом посте я опишу алгоритм процедурной генерации уровней двухмерного подземелья с заранее заданной структурой. В первой части будет представлено общее описание, а во второй — реализация алгоритма.

Введение

Алгоритм был написан как часть работы на получение степени бакалавра и основан на статье Ma et al (2014). Целью работы было ускорение алгоритма и дополнение его новыми функциями. Я вполне доволен результатом, потому что мы сделали алгоритм достаточно быстрым, чтобы использовать его во время выполнения игры. После завершения бакалаврской работы мы решили превратить её в статью и отправить на конференцию Game-ON 2018.

Алгоритм

Для создания уровня игры алгоритм получает в качестве входных данных набор полигональных строительных блоков и граф связности уровня (топологию уровня). Узлы графа обозначают комнаты, а рёбра определяют связи между ними. Цель алгоритма — назначить каждому узлу графа форму и расположение комнаты таким образом, чтобы никакие две формы комнат не пересекались, и каждая пара соседних комнат могла соединяться дверьми.

(a)

(b)

©

(d)

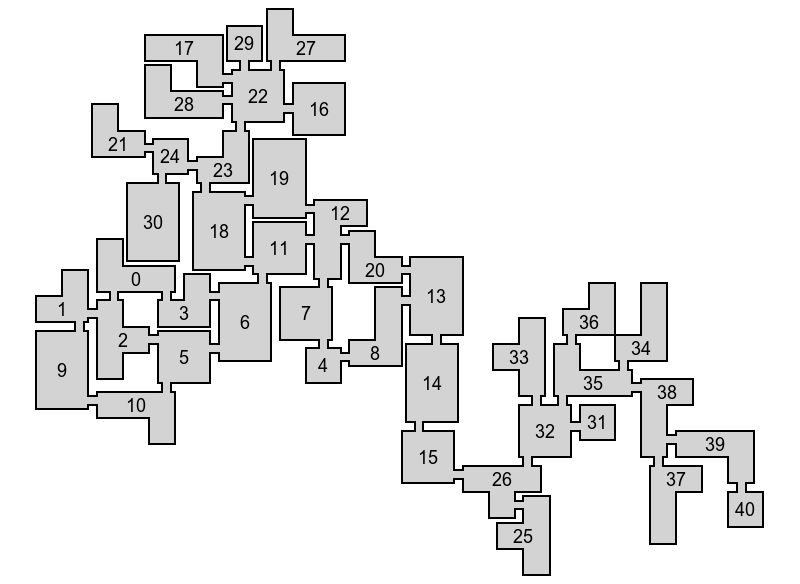
На рисунках © и (d) показаны схемы, сгенерированные из входного графа (a) и строительных блоков (b).

С помощью графа связности дизайнер игры может с лёгкостью управлять течением игрового процесса. Вам нужна один общий путь к комнате босса с несколькими необязательными побочными путями? Просто начните с графа пути и затем задайте несколько узлов, в которых игрок может выбрать: или идти по основному пути, или исследовать побочный, с ожидающими его возможными сокровищами и/или монстрами. Вам нужно срезать путь? Просто выберите два узла в графе и добавьте соединяющую их короткую дорогу. Возможности этой схемы бесконечны.

Примеры входных графов. Основной путь показан красным, вспомогательные — голубым, короткий путь — оранжевым.

Алгоритм не только позволяет дизайнерам игр управлять высокоуровневой структурой генерируемых карт, но и предоставляет возможности управления внешним видом отдельных комнат и способами их соединения друг с другом.

Разные формы для разных комнат

Я упоминал комнату босса в конце уровня. Мы ведь не хотим, чтобы комната с боссом выглядела как любая другая обычная комната, правда? Алгоритм позволяет задавать формы для каждой комнаты. Например, мы можем создать комнату начала уровня и комнату босса, которые должны иметь собственные наборы форм комнат, и один общий набор для всех других комнат.

Две схемы, сгенерированные из входного графа, в которых с комнатой номер 8 связана особая форма комнат.

Явно указываемые позиции дверей

Представьте, что у вас есть качественный скрипт встречи с боссом, и что нам нужно, чтобы игрок вошёл в комнату босса с определённого тайла. Или у нас может быть шаблон комнаты, в котором некоторые тайлы зарезервированы под стены и другие препятствия. Алгоритм позволяет дизайнерам явным образом задавать возможные позиции дверей для отдельных форм комнат.

Но иногда цель может быть противоположной. Мы можем создать шаблоны комнат таким образом, что двери в них могут быть практически где угодно. Благодаря этому мы накладываем на алгоритм меньше ограничений, поэтому часто он выполняется быстрее, а сгенерированные схемы могут казаться менее монотонными и более органичными. Для таких ситуаций есть возможность просто указывать длину дверей и насколько далеко они должны находиться от углов. Расстояние от углов — это своего рода компромисс между ручной расстановкой всех дверей и наличием дверей в любом месте.

(a)

(b)

Рисунок (a) иллюстрирует различные типы размещения дверей — у квадратной комнаты есть 8 чётко заданных позиций дверей, а в прямоугольной комнате используется длина и расстояние от углов. На рисунке (b) показана простая сгенерированная схема с формами комнат из рисунка (a).

Коридоры между комнатами

Когда мы говорим об уровнях подземелья, то часто представляем комнаты, соединённые узкими коридорами. Хочется считать, что соединения на входном графе обозначают коридоры, однако они ими не являются. Они просто гарантируют, что все соседние узлы будут напрямую соединены дверьми. Если мы хотим, чтобы комнаты соединялись коридорами, то нужно вставить новый узел между всеми парами соседних комнат и притвориться, что это комнаты-коридоры (с определёнными формами комнат и заданными позициями дверей).

(a)

(b)

Иллюстрация того, как мы можем изменить входной граф, чтобы добавить коридоры между комнатами. Рисунок (a) показывает входной граф до добавления комнат-коридоров. На (b) показан входной граф, созданный из (a) добавлением новых комнат между всеми соседними комнатами исходного графа.

К сожалению, так мы сильно усложняем задачу алгоритма, потому что часто количество узлов при этом удваивается. Поэтому я реализовал версию алгоритма, учитывающего коридоры, который позволяет снизить снижение производительности при расположении комнат-коридоров. На данный момент алгоритм поддерживает или коридоры между всеми комнатами, или полное отсутствие коридоров, но в будущем я планирую сделать его более гибким.

Примеры

Несколько схем, сгенерированных из разных наборов строительных блоков и со включенными коридорами.

Несколько схем, сгенерированных из разных наборов строительных блоков со включенными и отключенными коридорами.

Во второй части поста я расскажу о внутренней работе алгоритма.

Также я работаю над плагином Unity для процедурной генерации подземелий, в который будет включён этот алгоритм. Я делаю это потому, что несмотря на возможность использования этого алгоритма непосредственно в Unity (он написан на C#), удобство работы с ним далеко от идеала. На создание шаблонов комнат без GUI уходит очень много времени, а для преобразования выходных данных алгоритма в используемое внутри игры представление нужно очень много кода.

Так как сам я не являюсь разработчиком игр, моя цель заключается в том, чтобы сделать плагин достаточно хорошим для использования другими людьми. Если всё пройдёт хорошо, то я постараюсь опубликовать обновления, когда у меня будет рассказать о чём-то интересном. У меня есть уже довольно много идей о самом генераторе и о тестировании его возможностей.

Скриншоты плагина Unity (проект находится в процессе разработки)

Часть 2. Реализация алгоритма

В этой части я расскажу об основных идеях, заложенных в фундамент алгоритма, описанного в первой части поста. Изначально я хотел описать базовые концепции вместе с основными усовершенствованиями, необходимыми для того, чтобы алгоритм был достаточно быстрым. Однако, как оказалось, даже основных концепций более чем достаточно для этого поста. Поэтому я решил раскрыть улучшения производительности в будущей статье.

Мотивация

Прежде чем переходить к реализации, я хочу показать результат того, что мы будем делать. В показанном ниже видео демонстрируется 30 разных схем, сгенерированных из одного входного графа и одного набора строительных блоков. Алгоритм всегда останавливается на 500 мс после генерации схемы, а затем пытается сгенерировать следующую.

Как это работает

Цель алгоритма — назначить форму и позицию комнаты каждому узлу графа таким образом, чтобы никакие две комнаты не пересекались, а соседние комнаты были соединены дверьми.

Один из способов достичь этого — попробовать все возможные комбинации форм комнат и их позиций. Однако, как можно догадаться, это будет очень неэффективно, и мы, вероятно не сможем сгенерировать схемы, даже основанные на очень простых входных графах.

Вместо поиска по всем возможным комбинациям алгоритм вычисляет, как можно корректно соединить все отдельные комнаты (так называемые пространства конфигураций) и использует эту информацию, чтобы направить поиск. К сожалению, даже имея эту информацию, всё равно довольно сложно найти правильную схему. Поэтому для эффективного исследования пространства поиска мы используем вероятностную технику оптимизации (в данном случае имитацию отжига). А для дальнейшего ускорения оптимизации мы разбиваем входную задачу на более мелкие и простые в решении подзадачи. Это выполняется разделением графа на меньшие части (называемые цепями) с последующим созданием схем для каждой из них по порядку.

Пространства конфигураций

Для пары многоугольников, в которой один закреплён на месте, а другой может свободно перемещаться, пространство конфигураций является множеством таких позиций свободного многоугольника, при которых два многоугольника не пересекаются и могут соединяться дверьми. При работе с многоугольниками каждое пространство конфигураций можно представить как возможно пустое множество линий и вычислить простейшими геометрическими инструментами.

(a)

(b)

Пространства конфигураций. На рисунке (a) показано пространство конфигураций (красные линии) свободного прямоугольника относительно закреплённого Г-образного многоугольника. Оно определяет все местоположения центра квадрата, при которых два блока не пересекаются и касаются друг друга. Рисунок (b) показывает пересечение (жёлтые точки) пространств конфигураций подвижного квадрата относительно двух закреплённых прямоугольников.

Для вычисления пространства конфигураций одного закреплённого и одного свободного блоков используется следующий алгоритм. Мы выбираем на подвижном блоке опорную точку и рассматриваем все локации в , такие, что при перемещении многоугольника так, что его опорная точка располагается в этой локации, и подвижный, и закреплённый блок касаются друг друга, но не пересекаются. Множество всех таких точек образует пространство конфигураций двух блоков (рисунок (a) сверху). Чтобы получить пространство конфигураций подвижного блока относительно двух или более закреплённых блоков, вычисляется пересечение отдельных пространств конфигураций (рисунок (b) сверху).

Алгоритм использует пространства конфигураций двумя способами. Во-первых, вместо того, чтобы пробовать случайные позиции отдельных комнат, мы используем пространства конфигураций для поиска позиций, ведущих к как можно большему количеству соединяемых дверьми соседних комнат. Для этого нужно получить максимальное непустое пересечение пространств конфигураций соседей. Во-вторых, мы используем пространства конфигураций для проверки того, все ли пары соседних комнат можно соединить дверьми. Это выполняется проверкой того, находится ли позиция комнаты внутри пространства конфигураций всех её соседей.

Так как формы комнат во время выполнения игры не меняются, мы можем предварительно вычислить пространства конфигураций всех пар форм комнат ещё до запуска алгоритма. Благодаря этому значительно ускоряется весь алгоритм.

Инкрементная схема

При решении сложной задачи один из возможных подходов — разделить её на более мелкие и простые подзадачи, и решать уже их. Именно так мы и поступим с задачей размещения отдельных комнат. Вместо того, чтобы располагать все комнаты за раз, мы разобьём входной граф на меньшие подграфы и попытаемся один за другим создать схемы из них. Авторы первоначального алгоритма называют эти подграфы «цепями» из-за самого принципа этих графов, в которых каждый узел имеет не более двух соседей, и поэтому создать их схему довольно просто.

Окончательной выходной схемой всегда является один соединённый компонент, поэтому нет никакого смысла соединять в схемы отдельные компоненты, а потом пытаться объединить их, потому что процесс объединения может быть довольно сложным. Поэтому после размещения цепи следующей соединяемой цепью всегда будет та, которая соединена с уже выстроенными в схему вершинами.

Layout GenerateLayout(inputGraph) {
    var emptyLayout = new Layout();
    var stack = new Stack();
    stack.Push(emptyLayout);

    while(!stack.Empty()) {
        var layout = stack.Pop();
        var nextChain = GetNextChain(layout, inputGraph);
        Layout[] partialLayouts = AddChain(layout, nextChain);

        if (!partialLayouts.Empty()) {
            if (IsFullLayout(partialLayouts[0])) {
                return partialLayouts[0];
            } else {
                stack.Push(partialLayouts);
            }
        }
    }

    return null;
}

Псевдокод, демонстрирующий инкрементный подход к нахождению правильной схемы.

Показанный выше псевдокод демонстрирует реализацию инкрементной схемы. На каждой итерации алгоритма (строки 6 — 18) мы сначала берём последнюю схему из стека (строка 7) и вычисляем, какую цепь нужно добавить следующей (строка 8). Это можно сделать, просто сохранив номер последней цепи, добавленной к каждой частичной схеме. Следующим шагом мы добавляем к схеме следующую цепь (строка 9), генерируя несколько развёрнутых схем, и сохраняем их. Если этап расширения оканчивается неудачей, но в стек не добавляется новых частичных схем, и алгоритму нужно продолжать с последней сохранённой частичной схемой. Мы называем эту ситуацию поиском с возвратом, потому что алгоритм не может расширить текущую частичную схему и должен вернуться назад и продолжить с другой сохранённой схемой. Обычно это необходимо, когда не хватает места для соединения дополнительных цепей к уже составленным в схемы вершинам. Также поиск с возвратом является причиной того, что мы всегда пытаемся сгенерировать несколько расширенных схем (строка 9). В противном случае нам бы не было к чему возвращаться. Процесс завершается, когда мы сгенерируем полную схему, или стек опустеет.

(a) Входной граф

(b) Частичная схема

© Частичная схема

(d) Полная схема

(e) Полная схема

Инкрементная схема. На рисунках (b) и © показаны две частичные схемы после планировки первой цепи. На (d) показана полная схема после расширения (b) второй цепью. На рисунке (e) показана полная схема после расширения © второй цепью.

Чтобы разделить граф на части, нужно найти плоское вложение входного графа, то есть чертёж на плоскости, в котором рёбра пересекаются только в конечных точках. Это вложение используется затем для получения всех граней графа. Основная идея разложения заключается в том, что из циклов сложнее создать схему, потому что у их узлов больше ограничений. Поэтому мы пытаемся расположить циклы в начале разложения, чтобы они были обработаны как можно раньше и снизить вероятность необходимости возврата назад на последующих этапах. Первая цепь разложения образуется наименьшей гранью вложения, а последующие грани добавляются затем в порядке поиска в ширину (breadth-first search). Если существуют другие грани, которые можно выбрать, то используется наименьшая из них. Когда граней не остаётся, добавляются оставшиеся нециклические компоненты. На рисунке 4 показан пример разложения в цепи, который получен в соответствии с этими этапами.

(a)

(b)

Разложение на цепи. На рисунке (b) показан пример того, как можно разложить на цепи рисунок (a). Каждый цвет обозначает отдельную цепь. Числа обозначают порядок создания цепей.

© Хорошая частичная схема

(d) Полная схема

(a) Входной граф

(b) Плохой частичный граф

Поиск с возвратом. На рисунке (b) показан пример плохой частичной схемы, потому что в ней недостаточно пространства для соединения узлов 0 и 9. Для генерации полной схемы (d) необходим возврат к другой частичной схеме ©.

Имитация отжига

Алгоритм имитации отжига — это вероятностная техника оптимизации, цель которой — исследование пространства возможных схем. Она была выбрана авторами исходной статьи, потому что оказалась полезной в подобных ситуациях в прошлом. При реализации алгоритма я решил использовать тот же метод, потому что хотел начать с того, что уже доказало свою эффективность при решении этой задачи. Однако я думаю, что его можно заменить другим методом и моя библиотека написана таким образом, чтобы процесс замены метода был достаточно простым.

Алгоритм имитации отжига итеративно оценивает небольшие изменения в текущей конфигурации, или схеме. Это значит, что мы создаём новую конфигурацию, случайным образом выбирая один узел и меняя его позицию или форму. Если новая конфигурация улучшает функцию энергии, то принимается всегда. В противном случае есть небольшая вероятность принятия конфигурации в любом случае. Вероятность принятия худших решений со временем уменьшается. Функция энергии создана таким образом, что накладывает большие штрафы на пересекающиеся узлы и не касающиеся друг друга соседние узлы.

A — это общая площадь пересечения между всеми парами блоков в схеме. D — это сумма квадратов расстояний между центрами пар блоков, во входном графе являющихся соседями, но не касающихся друг друга. Значение влияет на вероятность того, что имитации отжига разрешено будет перейти к худшей конфигурации; этот параметр вычисляется из средней площади строительных блоков.

После выбора узла для изменения мы меняем или его форму, или позицию. Как мы выбираем новую позицию? Можно выбирать её случайным образом, но это часто будет ухудшать функцию энергии, а алгоритм будет сходиться очень медленно. Можем ли мы выбрать позицию, которая с большой вероятностью увеличит функцию энергии? Понимаете, к чему я веду? Мы используем пространства конфигураций, чтобы выбрать позицию, удовлетворяющую ограничениям наибольшего количества соседних комнат.

Затем для изменения формы достаточно просто выбрать одну из доступных форм комнат. Пока алгоритм не пытается решать, какая форма с наибольшей вероятностью приведёт нас к правильной схеме. Тем не менее, было бы интересно попробовать эту возможность и посмотреть, ускорит ли она работу алгоритма.

List AddChain(chain, layout) {
    var currentLayout = GetInitialLayout(layout, chain);
    var generatedLayouts = new List();

    for (int i = 1; i <= n, i++) {
        if (/* мы уже сгенерировали достаточное количество схем */) {
            break;
        }

        for (int j = 1; j <= m, j++) {
            var newLayout = PerturbLayout(currentLayout, chain);

            if (IsValid(newLayout)) {
                if (DifferentEnough(newLayout, generatedLayouts)) {
                    generatedLayouts.Add(newLayout);
                }
            }

            if (/* newLayout лучше, чем currentLayout */) {
                currentLayout = newLayout;
            } else if (/* вероятность, зависящая от того, насколько плоха энергия newLayout */) {
                currentLayout = newLayout;
            }
        }

        /* уменьшаем вероятность принятия худших схем */
    }

    return generatedLayouts;
}

Это псевдокод метода, отвечающего за создание схемы отдельной цепи с помощью имитации отжига.

Чтобы ускорить весь процесс, мы попытаемся найти исходную конфигурацию с низкой энергией. Для этого мы упорядочим узлы в текущей цепи по поиску в ширину, начиная с тех, которые являются соседними к уже включённым в схему узлам. Затем упорядоченные узлы размещаются по одному и для них из пространства конфигураций выбирается позиция с наименьшей энергией. Здесь мы не выполняем никакого возврата назад — это простой жадный процесс.

Бонусное видео

В показанном ниже видео демонстрируются схемы, сгенерированные из того же входного графа, что и в первом видео. Однако на этот раз показан инкрементный подход. Можно заметить, что алгоритм добавляет цепи узлов по одному. Также видно, что иногда присутствуют две последовательные частичные схемы с одинаковым количеством узлов. Это происходит, когда алгоритм выполняет возврат назад. Если первые попытки добавить другую цепь к первой частичной схеме заканчиваются неудачей, то алгоритм пробует другую частичную схему.

Скачиваемые материалы

Реализацию алгоритма на .NET можно найти в моём github. Репозиторий содержит DLL .NET и GUI-приложение WinForms, управляемое файлами конфигурации YAML.

© Habrahabr.ru