[Перевод] Естественность и Стандартная Модель
Что такое «естественность?»
Что имеют в виду специалисты по физике частиц и теории струн, говоря, что определённый набор частиц и взаимодействий является «естественным»? Они не имеют в виду то, что он является «частью природы». Во Вселенной всё по определению является частью природы.
У слова «естественный» есть много значений. Учёные в нашем контексте используют не значение «связанный с природой», а значение «типичный» или «обобщённый», «ожидаемый», «обычный». Например: «естественно, ребёнок, ударившись головой, заорал», или «естественно, ближе к центру жить стоит дороже», или «я не носил эти очки много месяцев, и они, естественно, запылились». А неестественно — это когда ребёнок не кричит, когда в центре города дёшево, и когда очки чистые. Обычно, когда происходит что-то неестественное, тому есть причина.
В большинстве контекстов физики частиц и связанных с этой тем сюрпризы встречаются крайне редко. Это значит, что взглянув на физическую систему, вы увидите, что она ведёт себя так, как вы, набрав некоторого научного опыта, можете от неё ожидать. А если она так себя не ведёт, то, как показывает опыт, тому есть причина. А если эта причина неочевидна, то неестественное поведение системы может говорить о каком-то экстремальном эффекте, который вам пока неизвестен.
Для наших целей понятие естественности важно потому, что в природе есть два больших сюрприза, с которыми приходится сталкиваться нам, специалистам по физике частиц, и нашим друзьям. Первый — то, что космологическая постоянная (которую часто называют тёмной энергией) удивительно маленькая по сравнению с тем, чего можно было бы ожидать естественным образом. Второй — что иерархия между силой гравитации и силой других взаимодействий удивительно большая, по сравнению с тем, чего можно было бы ожидать.
Второй сюрприз можно переформулировать так: Стандартная Модель (совместно с теорией гравитации Эйнштейна) — набор уравнений, используемых нами для предсказания поведения всех известных элементарных частиц и сил — удивительно, чрезвычайно, невероятно неестественная теория. В физике есть ещё только один аспект — возможно, единственный аспект во всей науке — ещё менее естественный, чем Стандартная Модель, и это космологическая постоянная.
Понятия естественного и неестественного
Полагаю, что концепцию естественности лучше всего опишет одна история.
Пара моих друзей из колледжа, назовём их Аня и Стив, поженились, и теперь у них есть двое детей-подростков. Когда эти дети были моложе — им было 4 и 7 лет — они вели себя, как дикари. Жёстко играли, обижались друг на друга, швырялись вещами, и за ними постоянно приходилось присматривать.
Однажды Аня купила очень красивые цветы и поставила их в любимую стеклянную вазу. Но до того, как она успела поставить вазу на кухонный стол, в дверь позвонили. Она побежала с вазой к двери, и по пути, не подумав, поставила вазу на небольшой неустойчивый столик, стоявший рядом со стеной детской игровой комнаты.
Через полчаса Стив вернулся домой с детьми, и отправил их в игровую комнату, чтобы они там побыли, пока они с Аней пришли бы в себя после рабочего дня и приготовили ужин. Они слышали обычные звуки: удары, падения, звук отскакивающих мячей и падающих игрушек, крики «нечестно» и «прекрати», крик, который закончился почти сразу же после того, как начался.
Через 45 минут Аня заметила, что вазы с цветами на кухонном столе нет. Поискав её в кухне и в столовой, она внезапно вспомнила, что поставила её и забыла в самом опасном месте дома.
Она побежала в игровую комнату, надеясь, что не опоздала. И что вы думаете, она нашла там, когда открыла дверь?
Догадайтесь. У вас есть три варианта (рис. 1). Выберите наиболее вероятный:
1. Ваза стояла там же, где она её оставила, аккуратно расположившись в центре стола.
2. Ваза была разбита, и раздавленные цветы валялись на полу.
3. Ваза свисала со стола прямо на краю, в миллиметре от катастрофы.
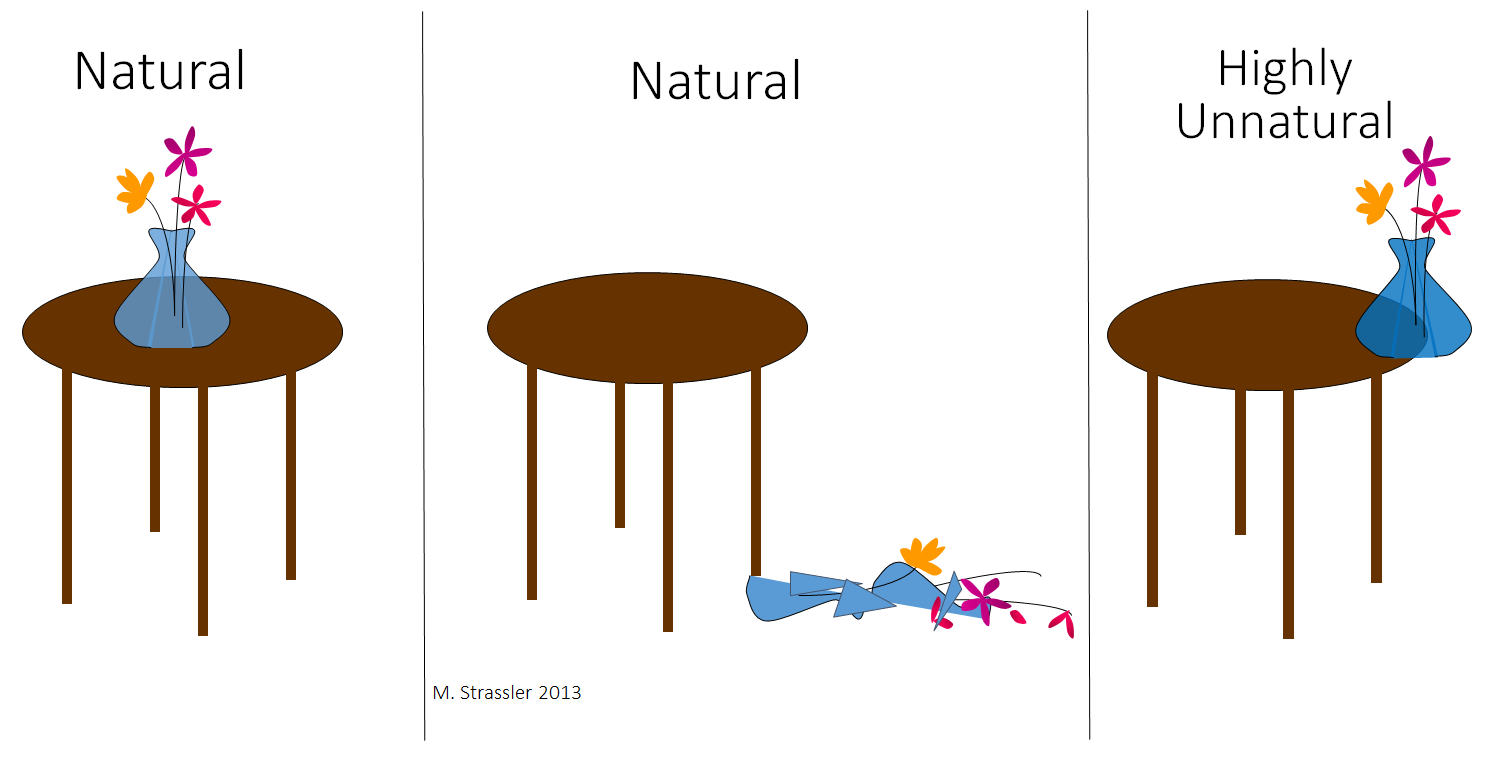
Рис. 1
Правильный ответ: №3. Она свисала с края.
Подозреваю, вы мне не верите. По крайней мере, если даже и верите, то считаете, что для случившегося должно быть какое-то сложное объяснение, и я его вам дам. Невероятно, чтобы два маленьких ребёнка бесились в комнате и каким-то образом случайно довели вазу до такого ненадёжного расположения. Поскольку то, что ваза была именно там — не стоя прочно на столе, не упав на пол, а где-то посередине — это же… неестественно!
Тому должно быть объяснение.
Может, с краю стола был клей, и ваза прилипла к нему перед тем, как упасть? Может, один из детей прятался за столом и держал вазу, чтобы разыграть маму? Может, её муж завязал вокруг вазы ниточку и прикрепил её к столу, или к потолку, чтобы ваза не падала? Может, ваза и стол намагничены?
Что-то настолько неестественное не могло случиться само по себе. Особенно в комнате, в которой два ребёнка бесятся и швыряются вещами.
Неестественное естество Стандартной Модели
Теперь обратимся к Стандартной Модели, скомбинированной с Эйнштейновской теорией гравитации.

Рис. 2
Представьте себе похожую на нашу Вселенную, описываемую полным набором уравнений — на языке теоретической физики это называется теорией — похожим на Стандартную Модель (плюс гравитация). Для простоты допустим, что в этой Вселенной есть все те же самые элементарные частицы и взаимодействия, что и в нашей. Отличие состоит в том, что сила взаимодействий, и сила, с которой поле Хиггса взаимодействует с другими известными частицами и с самим собой (что в результате определяет массу известных частиц), немного отличается от нашей — допустим, на 1%, 5% или даже на 50%. Вообще, давайте представим ВСЕ такие вселенные. Все вселенные, описываемые уравнениями типа Стандартной Модели, в которых сила взаимодействий всех полей и частиц друг с другом меняется вплоть до 50%. На что будут похожи миры, описываемые этими немного отличающимися уравнениями (миры показаны на рис. 2 в виде кучки?)
Среди воображаемых миров мы найдём три основных класса со следующими свойствами.
1. Среднее значение поля Хиггса равно нулю; то есть, поле Хиггса отключено. В таких мирах масса частицы Хиггса будет в десять тысяч триллионов (10 000 000 000 000 000) раз больше, чем в нашем. Все остальные известные элементарные частицы будут безмассовыми (за исключением некоторых отдельных особенностей). В частности, у электрона не будет массы, и в этом мире не будет никаких атомов.
2. Поле Хиггса включено на полную. Его среднее значение, и масса частицы Хиггса, и масса всех известных частиц, будет в десять тысяч триллионов (10 000 000 000 000 000) раз больше, чем в нашей вселенной. В таком мире не будет атомов или привычных нам крупных объектов. К примеру, там не сможет сформироваться ни звезда, ни планета — они обязательно сколлапсируют в чёрную дыру.
3. Поле Хиггса включено на небольшую величину. Его среднее значение примерно соответствует нашему — возможно, в несколько раз больше или меньше, но сравнимо. Массы известных частиц, хотя и будут отличаться от тех, что есть в нашем мире, но не сильно. И все частицы, у которых в нашем мире есть масса, будут обладать массой. В некоторых из этих миров даже смогут появляться атомы, планеты и другие структуры. В иных могут быть экзотические и непривычные нам вещи. Но по крайней мере некоторые базовые свойства таких миров будут нам знакомы.
Какая же доля миров попадает в класс №3? Среди всех рассматриваемых нами теорий типа Стандартной Модели какая доля будет хоть немного напоминать нашу?
До смешного, до абсурдного малая доля (рис. 3). Если вы выберете Вселенную случайным образом из нашего набора миров, похожих на Стандартную Модель, то шанс, что он будет хоть немного напоминать наш, будет невероятно меньше того, что вы беспечно оставили вазу на столе и она оказалась на краю катастрофы чисто случайно.

Рис. 3
Иначе говоря, если Стандартная Модель (плюс гравитация) описывает всё, что существует в нашем мире, тогда среди всех возможных миров мы живём в чрезвычайно необычном — таком же неестественном, как ваза, отстоящая на ширину одного атома от падения со стола. Классы 1 и 2 вселенных естественные, типичные, обобщённые. Большая часть теорий типа Стандартной Модели выдаст вселенную из этих классов. В класс 3, в который входит и наша Вселенная, включает в себя возможные, но неестественные и нетипичные миры. То, что нам выпало жить в такой необычной вселенной — особенно, поскольку мы живём, что довольно естественно, на обычной планете, вращающейся вокруг обычной звезды в обычной галактике — неожиданно, шокирующе, и странно. И заслуживает, как и странно расположенная ваза, объяснения. Однозначно приходится подозревать о существовании скрытого механизма, чего-то, связанного со вселенной, что пока нам неизвестно, что позволяет нашей вселенной естественно жить на краю.
А аналогия играющих детей, подвергающих вазу опасности и делающих её сбалансированное расположение маловероятным? Это сама квантовая механика — основные принципы работы мира. Квантовые эффекты не умеют мирно сосуществовать со случайным и нестабильным балансом.
Чуть позже я перейду к обсуждению квантовых эффектов и того, как они делают Стандартную Модель неестественной. Но сначала, хотя я и надеюсь, что вам понравилась моя история, я хочу отметить, что между вазой на столе и вселенной есть одно важное отличие. Если кто-нибудь ударит по столу с вазой она, вероятно, упадёт, или, если нам повезёт, соскользнёт к центру стола. В иных мирах она легко может сдвинуться со своей шаткой позиции. Для нашей вселенной, наоборот, не существует опасности плавно изменить свои свойства и превратиться во вселенную классов 1 или 2. Хотя возможно, что когда-нибудь она внезапно изменится и станет совсем другой благодаря процессу под названием тунеллирование или вакуумный распад, это событие непредставимо далеко от нас. Беспокоиться об этом не стоит.
Реальная проблема вселенной находится в прошлом: как, среди огромного количества возможных вселенных, мы оказались в такой неестественной? Есть ли в нашей вселенной что-то такое, чего мы пока не знаем, что делает её не такой неестественной, как она кажется? Или же с этим как-то связано то, что многие (большинство) естественных вселенных не приспособлены для жизни? Или, возможно, люди ещё недостаточно умны, и этому существует другое научное объяснение? Какой бы ни была эта причина, она либо связана с фактом вне времени, либо с чем-то, что случилось очень давно; вселенная (точнее, по крайней мере тот участок, который мы можем наблюдать глазами и телескопами) оставался неизменно неестественным (если Стандартная Модель полностью его описывает) миллиарды лет, и в ближайшем будущем меняться не будет.
В любом случае, проследуем далее и разберёмся в квантовой физике, делающей описанную Стандартной Моделью (и гравитацией) вселенную такой невероятно необычной.
Квантовая физика и (не)естественность
Перед дальнейшим чтением необходимо сначала прочесть про квантовые флуктуации и их энергию. В той статье вы найдёте ещё одну проблему естественности: проблему космологической постоянной.
Вернёмся к Хиггсу (и другим схожим частицам)
Квантовые флуктуации полей и их вклад в плотность энергии пустого пространства (т.н. вакуумная энергия) играют в нашей истории большую роль. Но наша цель обязывает нас отставить проблему космологической постоянной и сконцентрироваться на частице Хиггса и на том, почему Стандартная Модель неестественная. Мы сделаем это не потому, что проблема космологической постоянной не очень важная, и не потому, что мы уверены, что две этих проблемы не связаны между собой. Но поскольку космологическая постоянная непосредственно связана с гравитацией, а проблема частицы Хиггса и естественность Стандартной Модели никак не связаны с гравитацией напрямую, вполне возможно, что они разрешаются разными способами. И каждая из двух проблем сама по себе нереально сложная; если нам придётся решать их одновременно, тогда всё будет ещё хуже. Так давайте пока отправим космологическую постоянную в уголок, чтобы она там прикорнула. Но мы будем помнить, что в комнате присутствует слон, которого мы не сможем игнорировать вечно.
Теперь к полю Хиггса. Нам нужно ответить на три очень важных вопроса, связанных с полем Хиггса и его частицей. Я сформулирую эти вопросы исходя из предположения, что Стандартная Модель верна, или почти верна. Но если это не так, не стоит волноваться: изучаемые идеи останутся по сути теми же самыми, даже если потребуется их немного перефразировать.
1. Поле Хиггса включено. Его среднее значение везде и всегда, по крайней мере, с самых ранних этапов жизни Вселенной, ненулевое. Почему?
2. Его среднее значение равно 246 ГэВ. Что его задаёт?
3. Масса частицы Хиггса равна примерно 125 ГэВ/с2. Что её задаёт?
Я объясню вам, как и почему эти вопросы связаны с проблемой зависимости энергии пустого пространства (часть которой проистекает из квантовых флуктуаций полей) от среднего значения поля Хиггса.
Величина поля Хиггса и энергия пустого пространства
Как определить среднее значение любого поля (не только поля Хиггса) по Вселенной? Ответ: среднее значение поля должно обладать следующим свойством: если вы немного изменяете его значение, увеличивая или уменьшая, тогда энергия пустого пространства должна увеличиться. Коротко говоря, значение поля должно быть таким, что энергия пустого пространства в этом случае будет находиться в минимуме — не обязательно в самом минимальном, но одном из локальных (если минимумов больше одного, то выбор конкретного из них может зависеть от истории Вселенной, или от более сложных вещей, которых я пока касаться не буду).
Пара примеров того, как энергия пустого пространства в нашей Вселенной, или в какой-то воображаемой вселенной, может зависеть от поля Хиггса, или от какого-то другого похожего поля, показано на рис. 4. В каждом из двух случаев я нарисовал два минимума, где может расположиться поле Хиггса –, но это случайный выбор. В других случаях минимумов может быть более двух, или только один. Из того, что в нашем мире поля Хиггса включено, следует, что в энергии вакуума вселенной существует минимум, для которого значение поля Хиггса равно 246 ГэВ. И хотя из предыдущего моего рассказа это не очевидно, мы уверены, исходя из того, что мы знаем о природе и об уравнениях, что не существует минимума, в котором поле Хиггса равно нулю, и поэтому в нашей Вселенной поле Хиггса не выключено. Так что в нашей Вселенной зависимость энергии вакуума от поля Хиггса, по-видимому, выглядит больше похожей на левую часть рисунка, чем на правую, но, как мы увидим, оно может быть непохожим ни на одну из них. Если Стандартная Модель описывает физику на гораздо больших энергиях и на куда как меньших расстояниях, чем те, что мы изучаем на Большом адронном коллайдере, тогда форма соответствующей кривой будет гораздо сложнее — как мы увидим позднее.

Рис. 4: по горизонтали — среднее значение поля Хиггса, по вертикали — плотность энергии. Масса частицы Хиггса задаётся искривлениями графика, формирующими минимумы.
Масса частицы Хиггса и энергия пустого пространства
Что насчёт массы частицы Хиггса? Она определяется (рис. 4) тем, как быстро энергия пустого пространства меняется при отклонении значения поля Хиггса от предпочитаемого. Почему?
Частица Хиггса — это маленькое возмущение поля Хиггса — то есть, при проходе частицы Хиггса полю Хиггса приходится немного меняться, оно становится то больше, то меньше. Поскольку мы знаем, что среднее значение поля Хиггса находится в минимуме энергии пустого пространства, любое небольшое изменение этого значения немного увеличивает эту энергию. Эта дополнительная энергия (на самом деле, её половина) и даёт энергию массы частицы Хиггса (через E = mc2). Если форма кривой вокруг минимума весьма плоская, то для изготовления частицы Хиггса требуется мало энергии, поскольку дополнительная энергия в возмущении поля Хиггса будет малой. Но если рядом с минимумом кривая сильно изогнута, тогда у частицы Хиггса большая масса.
Таким образом плоскость или заострённость кривой на графике в том месте, где находится значение поля Хиггса — кривизна в минимуме — определяет массу частицы Хиггса.
Почему сложно сделать массу частицы Хиггса маленькой
Измеренная масса частицы Хиггса примерно равна 125–126 ГэВ/с2, что где-то в 134 раза больше массы протона. Почему мы не можем просто подставить эту массу в наши уравнения и закончить с вопросом, откуда она взялась?
Проблема в том, что значение поля Хиггса, и масса частицы Хиггса не подставляются в используемые нами уравнения напрямую; они выводятся из используемых нами уравнений при помощи сложных расчётов. И тут мы сталкиваемся с определёнными трудностями.
Мы получаем эти два числа — среднее значение и массу поля и частицы — изучая то, как энергия пустого пространства зависит от поля Хиггса. И эта энергия, как и в любой теории поля, такой, как Стандартная Модель, является суммой многих вещей:
• энергии флуктуаций самого поля Хиггса,
• энергии флуктуаций поля верхнего кварка,
• энергии флуктуаций поля W,
• энергии флуктуаций поля Z,
• энергии флуктуаций поля нижнего кварка,
• энергии флуктуаций поля тау лептона,
• …
И так для всех полей в природе, непосредственно взаимодействующих с полем Хиггса. Схематически (настоящих энергий там нет) я изобразил их в виде синих кривых на рис. 5. Каждый график изображает одну составляющую энергии пустого пространства и то, как она изменяется, когда среднее значение поля Хиггса меняется от нуля до максимального значения, на которое у меня хватает смелости, и которое я назвал vmax.
Некоторые из вас могли читать о том, что эти вычисления энергии пустого пространства дают в ответе бесконечность. Это так, но это к делу не относится; это технический момент, истинный, если только принять vmax бесконечно большим — что явно не так. Я обнаружил, что многие люди, учёные и нет, считают (благодаря книгам людей, не являющихся экспертами, и предыдущему поколению экспертов — даже самого Фейнмана), что эти бесконечности важны и связаны с обсуждением естественности. Это не так. Мы ещё вернёмся к этому распространённому недопониманию, включающему подмену математическими тонкостями физически важных эффектов.

Рис. 5: какие вклады вносят в поле Хиггса разные поля, каким оно должно быть в итоге, и каким мы его наблюдаем в реальности
Что такое vmax? Это величина, до которой можно довести значение поля Хиггса, не теряя уверенности в том, что наши расчёты остаются в рамках Стандартной Модели. Под vmax я подразумеваю то, что если бы значение поля Хиггса было бы больше этой величины (что сделало бы массу верхнего кварка большей, чем примерно vmax/с2), тогда Стандартная Модель перестала бы точно описывать всё происходящее в физике частиц. Иначе говоря, vmax — граница между областью, в которой Стандартная Модель применима, и областью, где это не так.
Однако значение vmax нам неизвестно. И это неведение ещё сыграет свою роль. Судя по тому, что мы знаем из опытов на БАК, vmax должно быть порядка 500 ГэВ или более. Однако, из всего, что мы знаем, следует, что vmax может оказаться и в 10 000 000 000 000 000 раз больше этого. Дальше уже мы зайти не можем, поскольку там уже начинает играть роль гравитация. Если бы vmax была такой огромной, верхние кварки были бы такими тяжёлыми, что они превратились бы в крохотные чёрные дыры! А мы знаем, что Стандартная Модель такие явления не описывает. В этот момент уже должна вступать в силу квантовомеханическая версия гравитации –, а может и ещё раньше.
Итак, нам известно, что vmax находится где-то между 500 ГэВ и 1 000 000 000 000 000 000 ГэВ. На рис. 5 я предположил, что оно гораздо больше 500 ГэВ. Рассмотрим рис. 6, на котором она приближается к 500 ГэВ.
Каждый из вкладов, изображённых в верхнем ряду рис. 5, мы можем подсчитать (в принципе, а также, по большому счёту, и на практике) для любого поля Хиггса от нуля и до vmax, и для всех квантовых флуктуаций с энергиями менее vmax. (Тут я сильно упрощаю — на самом деле эта энергия Emax не должна быть точно такой же, как vmax, но давайте не будем усложнять сверх необходимого). Если vmax большое, тогда каждый из этих вкладов тоже очень большой — и, что важнее, варьирование, происходящее при изменении значения поля Хиггса от нуля до vmax, тоже очень большие — порядка vmax4 / (hc)3.
Но это ещё не всё. К этому необходимо добавить и другие вклады, показанные во втором ряду рис. 5, проистекающие из физических явлений, о которых мы пока не знаем ничего или почти ничего, из физики, которая напрямую не появляется в Стандартной Модели. Технически вклад этих эффектов неизвестной физики появляется в параметрах, определяющих уравнения Стандартной Модели в качестве входных данных. Но это входные данные, а не то, что мы рассчитываем, именно потому, что они поступают из неизвестных источников. В дополнение к эффектам квантовых флуктуаций известных полей с ещё большими энергиями, могут также существовать эффекты:
• квантовой механики гравитации,
• тяжёлых, пока не открытых нами частиц,
• взаимодействий, имеющих значение на расстояниях, более коротких, чем мы можем измерить;
• других, более экзотических вкладов от, к примеру, струн или D-бран в струнной теории, или какой-то ещё теории,
• что-то ещё…
Некоторые из них могут, прямо или косвенно, зависеть от значения поля Хиггса. Эти неизвестные эффекты я изобразил красным. Эти кривые на 100% взяты из головы. Мы не знаем об этих эффектах ничего, кроме того, что они могут существовать (а эффекты гравитации точно существуют), и что некоторые из них, или все они могут быть довольно большими. Такими же большими, или ещё больше тех, о которых мы знаем, изображённых в верхнем ряду. В принципе, все эти неизвестные эффекты могут быть нулевыми –, но это не решит проблемы естественности, как мы далее увидим, поэтому, можно предположить, что они ненулевые.
Важно тут что, что нет никаких очевидных причин полагать, будто неизвестные эффекты, нарисованные красным, каким бы то ни было образом связаны с известными эффектами, нарисованными синим. В самом деле, почему эффекты квантовой гравитации или какой-то новой силы, никак не связанной со слабым ядерным взаимодействием, должны быть как-то связаны с плотностью энергии квантовых флуктуаций поля верхнего кварка или поля W? Они выглядят концептуально раздельными источниками плотности энергии пустого пространства.
И вот, в чём загадка. Когда мы складываем все эти вклады в энергию пустого пространства, каждый из которых велик, а многие из которых очень сильно варьируются при изменении поля Хиггса от нуля до максимума, который мы можем рассматривать — мы обнаруживаем удивительно плоскую кривую, показанную зелёным. Рядом с вертикальной осью она почти идеально ровная. И всё же её минимум находится не в нуле поля Хиггса; он немного отходит от нуля, там, где значение поля Хиггса равно 246 ГэВ. Все эти различные вклады, синие и красные, изгибающиеся вверх и вниз под разными углами, почти идеально (но не совсем) взаимно уничтожают друг друга при сложении. Выглядит так, будто вы накидали несколько гор из Монтаны в глубокое ущелье Калифорнии, и получили равнину плоскую, как Канзас. Как это произошло?
Насколько серьёзна проблема? Насколько неожиданно это взаимное уничтожение? Ответ зависит от vmax. Если vmax равно всего 500 ГэВ, тогда никакого особенного взаимного уничтожения и не нужно — см. рис. 6. Но если vmax огромно, то взаимное уничтожение удивительно точное, как на рис. 5. Чем больше vmax, тем более удивительно взаимное уничтожение всех вкладов.

Рис. 6
Насколько удивительно? Взаимное уничтожение должно быть идеальным до одной части в (vmax/500 ГэВ)2. Так что если vmax близко к 500 ГэВ, в этом нет ничего удивительного;, но если vmax = 5000 ГэВ, нам нужно взаимное уничтожение до одной части на 100. Если оно равно 500 000 ГэВ, нам нужно взаимное уничтожение до одной части на миллион.
А если мы задерём значение vmax до максимального возможного — если Стандартная Модель описывает всю физику частиц без гравитации — тогда нам нужно взаимное уничтожение до одной части на 1 000 000 000 000 000 000 000 000 000 000.
В последнем случае невероятная точность взаимного уничтожения беспокоит особенно сильно. Это значит, что если бы вы поменяли массу частицы W или силу электромагнитного взаимодействия на чуть-чуть — допустим, на одну часть на миллион миллионов — то взаимное уничтожение сразу бы прекратилось, и теория перешла бы в класс 1 или класс 2, с ультра-тяжёлой частицей Хиггса, и либо с огромным, либо с нулевым значением поля Хиггса (см. рис. 3). Эта невероятная чувствительность означает, что свойства нашего мира с огромной точностью должны быть именно такими — как радио, настроенное на точную частоту нужной радиостанции с тонкой подстройкой. Такая экстремальная точная подстройка свойств физической системы не имеет прецедентов в науке.
Скажем иначе: Стандартная Модель, а конкретно, правильность Стандартной Модели при величинах vmax гораздо больших, чем 500 ГэВ, неестественна по причине взаимного уничтожения, показанного на рис. 5. В этом нет ничего типичного или обычного. И чем больше vmax, тем менее это естественно. Если вы возьмёте кучу обычных кривых, как те, что изображены на рис. 5, у каждой из которых есть минимумы и максимумы в точках, где значение поля Хиггса либо нулевое, либо примерно равно vmax, и сложите их вместе, вы обнаружите, что сумма этих кривых — это кривая со своими минимумами и максимумами в:
• точке со значением, сравнимым с vmax (теории класса 2 — см. рис. 3),
• или около нуля (теории класса 1),
•, но не где-то в промежутке от нуля и до очень-очень малой доли vmax (теории класса 3).
Более того, если кривые сильно изогнуты в районах минимумов и максимумов, их сумма типично тоже должна быть сильно искривлённой в районе её минимумов и максимумов (то есть, масса частицы Хиггса должна была бы быть примерно равной vmax/с2, как в теориях класса 1 и 2), и не должна быть чрезвычайно плоской в районе любого из её минимумов (как это нужно для того, чтобы частица Хиггса была бы гораздо легче, чем vmax/с2, как это получается в теориях класса 3). Это показано при помощи добавления всего двух кривых на рис. 7, где мы видим, что у двух кривых должна быть очень особенная связь для того, чтобы их сумма получилась очень плоской.

Рис. 7: сверху — сложение двух обычных, типичных кривых. Снизу — две нетипичные кривые с тонкой подстройкой.
Это проблема естественности. Проблема не только в том, что зелёная кривая на рис. 5 удивительно плоская, с минимумом там, где значение поля Хиггса очень мало. Проблема в том, что эта кривая — это выходные данные, сумма множества больших и, по всей видимости, не связанных между собой вкладов, и совершенно неочевидно, как сумма всех этих кривых принимает такую необычную форму.
Отступление по поводу бесконечностей, перенормировка и отрезы
Теперь, что касается всех этих бесконечностей, о которых вы могли слышать — вместе со страшным словом «перенормировка», в котором бесконечности каким-то образом заметаются под ковёр и приводят к конечным предсказаниям. Эти бесконечности, а также их устранение через перенормировку, иногда заставляют людей — даже учёных — утверждать, что специалисты физики частиц не понимают, что делают, и что из-за этого они приходят к проблеме естественности, которой на самом деле не существует.
Такие заявления весьма ошибочны. Эти технические проблемы (хорошо понимаемые сегодня) совершенно не относятся к нашему контексту.
Бесконечности, возникающие при определённых подсчётах массы частицы Хиггса и значения поля Хиггса — симптомы проблемы естественности, математические симптомы, проявляющиеся, когда вы настаиваете на увеличении vmax до бесконечности, что, хотя иногда и удобно, физически неверно. Бесконечности — не проблема естественности, они не находятся в её центре, и не являются её причиной.

Рис. 8
Среди множества способов это понять один из самых простых — изучить огромное разнообразие конечных теорий квантовых полей, открытых в 1980-х. У этих теорий есть ограниченное количество суперсимметрии, а ещё они конечные. Если взять такую теорию (рис. 8) и сломать суперсимметрию на масштабе vmax, но гарантировать, что в теории при более низких энергиях всё ещё будут поля с нулевым спином типа поля Хиггса, то никаких бесконечностей не появится. Более того, нет необходимости искусственным образом отрезать теорию на энергиях меньших vmax (как я сделал на рис. 5, отделив известное от неизвестного), поскольку в этом примере нам известны уравнения, которые можно использовать на энергиях как больших, так и меньших vmax. Энергию пустого пространства и её зависимость от различных полей можно подсчитать без всяких двусмысленностей, бесконечностей или бесконечной перенормировки. Так что же — есть ли и здесь проблема естественности? Приобретают ли частицы с нулевым спином массы порядка vmax/с2? Имеют ли поля с нулевым спином значения около нуля или примерно равные vmax? Ещё как! Никаких бесконечностей, никакого заметания под ковёр, никаких искусственных отрезов –, а проблема естественности остаётся такой же серьёзной.
Кстати, в этом рассуждении есть одна интересная уязвимость, связанная с тем, что мы узнали из теории струн по поводу квантовой теории поля. Но хотя она и приводит пример теорий, избегающих проблемы естественности, ни я, ни кто либо ещё не смог пока убедительно использовать их для реального решения проблемы естественности Стандартной Модели (вот, пожалуй, наилучшая попытка из всех).
Мы можем повторить такого рода вычисления с теорией струн (техническое упражнение, не требующее от нас веры в то, что теория струн на самом деле описывает природу). В вычислениях теории струн бесконечностей нет. Но если vmax, та шкала энергий, на которых Стандартная Модель перестаёт работать, будет гораздо больше, чем 500 ГэВ, то проблема естественности получается такой же серьёзной.
В общем: избавление от бесконечностей, возникающих в определённых подсчётах, связанных с Хиггсом, никак не помогает решить или повлиять на проблему естественности.
Решения проблемы естественности
Чисто с логической точки зрения на ум приходит пара качественно разных типов решений этой проблемы. [Эту часть профессор Страсслер, к сожалению, до сих пор не дописал — ждём… / прим. перев.]
