[Перевод] Декодируем JPEG-изображение с помощью Python

Всем привет, сегодня мы будем разбираться с алгоритмом сжатия JPEG. Многие не знают, что JPEG — это не столько формат, сколько алгоритм. Большинство JPEG-изображений, которые вы видите, представлены в формате JFIF (JPEG File Interchange Format), внутри которого применяется алгоритм сжатия JPEG. К концу статьи вы будете гораздо лучше понимать, как этот алгоритм сжимает данные и как написать код распаковки на Python. Мы не будем рассматривать все нюансы формата JPEG (например, прогрессивное сканирование), а поговорим только о базовых возможностях формата, пока будем писать свой декодер.
Введение
Зачем писать ещё одну статью про JPEG, когда об этом написаны уже сотни статей? Обычно в таких статьях авторы рассказывают лишь о том, что собой представляет формат. Вы не пишете код распаковки и декодирования. А если и напишете что-то, то на С/С++, и этот код будет недоступен широкому кругу людей. Я хочу нарушить эту традицию и показать вам с помощью Python 3, как работает базовый декодер JPEG. В его основе будет этот код, разработанный MIT, но я его сильно изменю ради удобочитаемости и понятности. Изменённый для этой статьи код вы найдёте в моём репозитории.
Разные части JPEG
Начнём с картинки, сделанной Ange Albertini. На ней перечислены все части простого JPEG-файла. Мы разберём каждый сегмент, и по мере чтения статьи вы не раз будете возвращаться к этой иллюстрации.
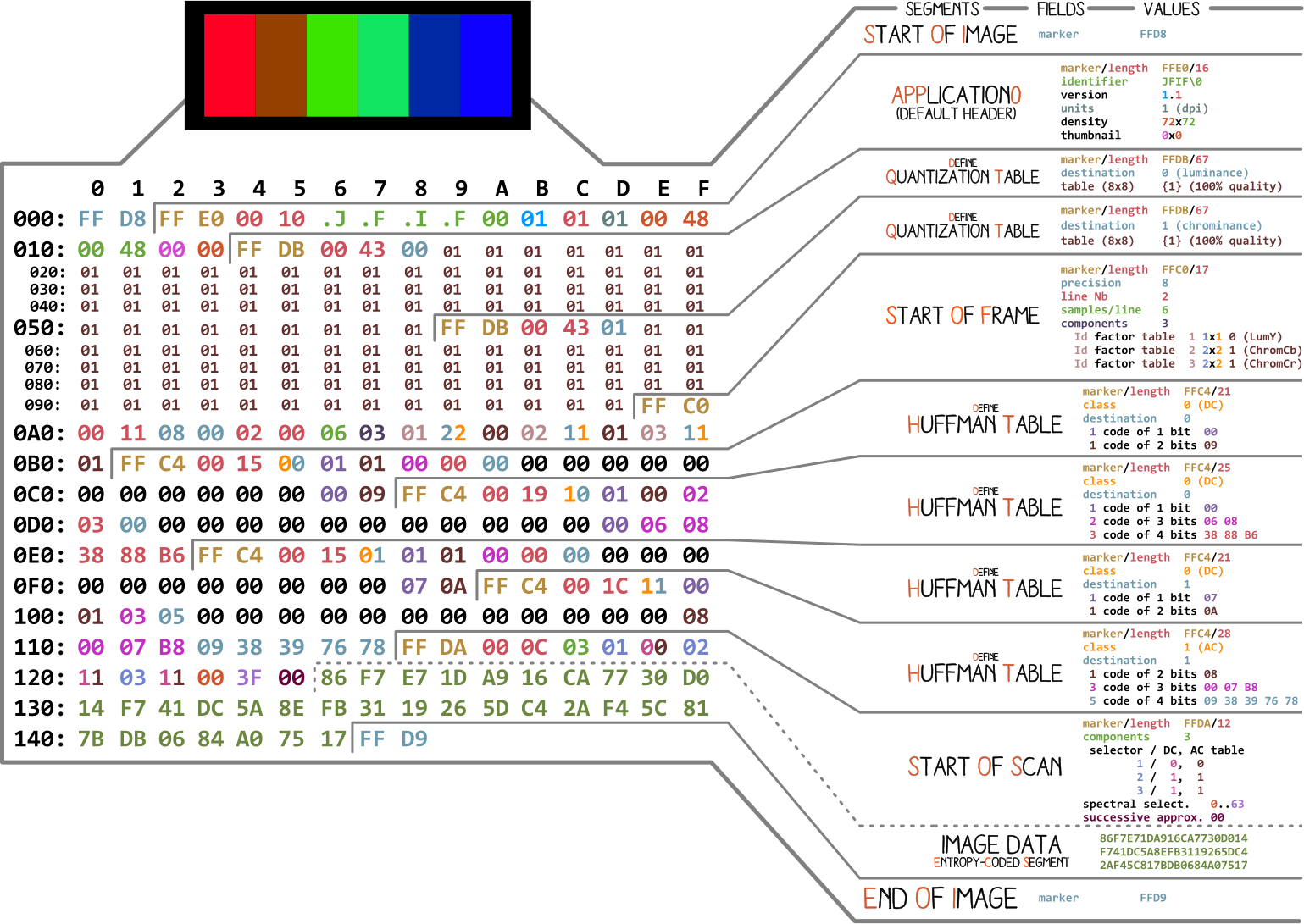
Почти каждый двоичный файл содержит несколько маркеров (или заголовков). Можете считать их своего рода закладками. Они крайне важны для работы с файлом и используются такими программами как file (на Mac и Linux), чтобы мы могли узнать подробности о файле. Маркеры указывают, где именно в файле хранится определённая информация. Чаще всего маркеры размещаются в соответствии со значением длины (length) конкретного сегмента.
Начало и конец файла
Самый первый важный для нас маркер — FF D8. Он определяет начало изображения. Если мы его не находим, то можно предположить, что маркер находится в каком-то другом файле. Не менее важен и маркер FF D9. Он говорит о том, что мы дошли до конца файла с изображением. После каждого маркера, за исключением диапазона FFD0 — FFD9 и FF01, сразу идёт значение длины сегмента этого маркера. А маркеры начала и конца файла всегда длиной два байта каждый.
Мы будем работать с этим изображением:

Давайте напишем код для поиска маркеров начала и конца файла.
from struct import unpack
marker_mapping = {
0xffd8: "Start of Image",
0xffe0: "Application Default Header",
0xffdb: "Quantization Table",
0xffc0: "Start of Frame",
0xffc4: "Define Huffman Table",
0xffda: "Start of Scan",
0xffd9: "End of Image"
}
class JPEG:
def __init__(self, image_file):
with open(image_file, 'rb') as f:
self.img_data = f.read()
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
elif marker == 0xffda:
data = data[-2:]
else:
lenchunk, = unpack(">H", data[2:4])
data = data[2+lenchunk:]
if len(data)==0:
break
if __name__ == "__main__":
img = JPEG('profile.jpg')
img.decode()
# OUTPUT:
# Start of Image
# Application Default Header
# Quantization Table
# Quantization Table
# Start of Frame
# Huffman Table
# Huffman Table
# Huffman Table
# Huffman Table
# Start of Scan
# End of Image
Для распаковки байтов изображения мы использовали struct. >H говорит struct, чтобы та считала тип данных unsigned short и работала с ними в порядке от старшего к младшему (big-endian). Данные в JPEG хранятся в формате от старшего к младшему. Только EXIF-данные могут быть в формате от младшего к старшему (little-endian) (хотя обычно это не так). А размер short равен 2, поэтому мы передаём unpack два байта из img_data. Как мы узнали, что это short? Мы знаем, что маркеры в JPEG обозначаются четырьмя шестнадцатеричными символами: ffd8. Один такой символ эквивалентен четырём битам (половине байта), поэтому четыре символа будут эквивалентны двум байтам, как и short.
После раздела Start of Scan сразу идут данные сканированного изображения, у которых нет определённой длины. Они продолжаются до маркера «конец файла», так что пока мы вручную «ищем» его, когда находим маркер Start of Scan.
Теперь разберёмся с остальными данными изображения. Для этого мы сначала изучим теорию, а потом перейдём к программированию.
Кодирование JPEG
Сначала поговорим о базовых концепциях и методиках кодирования, которые используются в JPEG. А кодирование будет выполняться в обратном порядке. По моему опыту, без этого разобраться в декодировании будет трудно.
Иллюстрация ниже пока что для вас непонятно, однако я буду давать вам подсказки по мере изучения процесса кодирования и декодирования. Здесь показаны этапы JPEG-кодирования (источник):
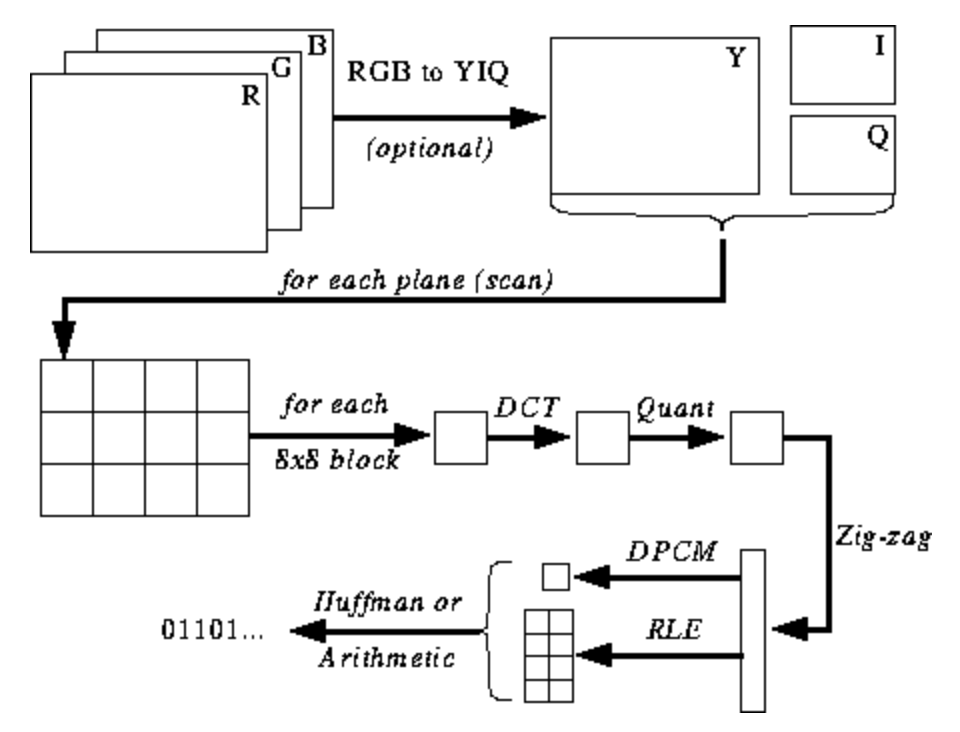
Цветовое пространство JPEG
Согласно спецификации JPEG (ISO/IEC 10918–6:2013 (E), раздел 6.1):
- Изображения, закодированные только с одним компонентом, считаются данными в градациях серого, где 0 — это чёрный, а 255 — белый.
- Изображения, закодированные с тремя компонентами, считаются RGB-данными, закодированными в пространстве YCbCr. Если изображение содержит сегмент маркера APP14, описанный в разделе 6.5.3, то цветовая кодировка считается RGB или YCbCr в соответствии с информацией в сегменте маркера APP14. Связь между RGB и YCbCr определяется в соответствии с требованиями ITU-T T.871 | ISO/IEC 10918–5.
- Изображения, закодированные с четырьмя компонентами, считаются CMYK-данными, где (0,0,0,0) означает белый цвет. Если изображение содержит сегмент маркера APP14, описанный в разделе 6.5.3, то цветовая кодировка считается CMYK или YCCK в соответствии с информацией в сегменте маркера APP14. Связь между CMYK и YCCK определяется в пункте 7.
В большинстве реализаций алгоритма JPEG вместо RGB используются яркость (luminance) и хроматичность (chrominance) (кодирование YUV). Это очень полезно, потому что человеческий глаз очень плохо различает высокочастотные изменения в яркости на маленьких участках, поэтому можно уменьшить частоту, и человек не заметит разницы. Что это даёт? Сильно сжатое изображение с почти незаметным снижением качества.
Как в RGB каждый пиксель кодируется тремя байтами цветов (красного, зелёного и синего), так и в YUV используется три байта, однако их значение другое. Компонент Y определяет яркость цвета (luminance, или luma). U и V определяют цвет (chroma): U отвечает за долю синего цвета, а V — за долю красного.
Этот формат был разработан в те времена, когда телевидение ещё не было столь привычным, и инженеры хотели использовать один формат кодирования изображения и для цветного, и для чёрно-белого телевещания. Подробнее об этом читайте тут.
Дискретное косинусное преобразование и квантование
JPEG преобразует изображение в блоки 8×8 пикселей (называются MCU, Minimum Coding Unit — минимальные единицы кодирования), меняет диапазон значений пикселей так, чтобы в центре было значение 0, затем применяет к каждому блоку дискретное косинусное преобразование и сжимает результат с помощью квантования. Давайте разберёмся, что всё это означает.
Дискретное косинусное преобразование (ДКП) — это метод преобразования дискретных данных в комбинаций косинусных волн. Превращение картинки в набор косинусов на первый взгляд выглядит бесполезным занятием, но вы поймёте причину, когда узнаете о следующих этапах. ДКП берёт блок 8×8 пикселей и говорит нам, как воспроизвести этот блок с помощью матрицы из 8×8 косинусных функций. Подробнее тут.
Матрица выглядит так:

Мы применяем ДКП отдельно к каждому компоненту пикселя. В результате получаем матрицу коэффициентов 8×8, которая показывает вклад каждой (из всех 64) косинусной функции во входной матрице 8×8. В матрице коэффициентов ДКП самые большие значения обычно находятся в левом верхнем углу, а самые маленькие — в правом нижнем. Левый верхний угол представляет собой самую низкочастотную косинусную функцию, а правый нижний — самую высокочастотную.
Это означает, что в большинстве изображений есть огромное количество низкочастотной информации и небольшая доля высокочастотной. Если правым нижним компонентам каждой матрицы ДКП присвоить значение 0, то получившееся изображение для нас будет выглядеть так же, потому что человек плохо различает высокочастотные изменения. Это мы и сделаем на следующем этапе.
Я нашёл отличное видео по этой теме. Посмотрите, если не понимаете смысла ДКП:
Все мы знаем, что JPEG — алгоритм сжатия с потерями. Но пока что мы ничего не потеряли. У нас есть только блоки 8×8 YUV-компонентов, преобразованные в блоки 8×8 косинусных функций без потери информации. Этап потери данных — это квантование.
Квантованием называют процесс, когда мы берём два значения из определённого диапазона и превращаем их в дискретное значение. В нашем случае это лишь хитрое название для сведения к 0 самых высокочастотных коэффициентов в получившейся ДКП-матрице. При сохранении изображения с помощью JPEG большинство графических редакторов спрашивают, какой уровень сжатия вы хотите задать. Здесь и происходит потеря высокочастотной информации. Вы уже не сможете воссоздать исходную картинку из получившегося JPEG-изображения.
В зависимости от степени сжатия используются разные матрицы квантования (забавный факт: большинство разработчиков имеют патенты на создание таблицы квантования). Мы поэлементно делим ДКП-матрицу коэффициентов на матрицу квантования, округляем результаты до целых чисел и получаем квантованную матрицу.
Рассмотрим пример. Допустим, есть такая ДКП-матрица:

А вот обычная матрица квантования:
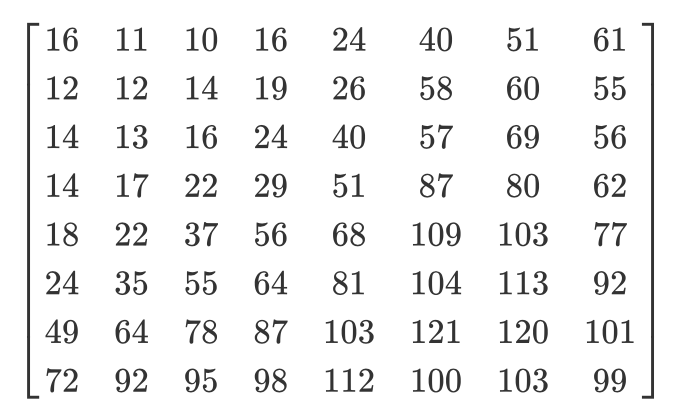
Квантованная матрица будет выглядеть так:

Хотя человек и не видит высокочастотную информацию, если вы удалите слишком много данных из блоков 8×8 пикселей, изображение станет выглядеть слишком грубо. В такой квантованной матрице самое первое значение называется DC-значением, а все остальные — AC-значениями. Если бы мы взяли DC-значения всех квантованных матриц и сгенерировали новую картинку, то получили бы превьюшку с разрешением в 8 раз меньше исходного изображения.
Также хочу отметить, что поскольку мы применяли квантование, нужно убедиться, что цвета попадают в диапазон [0,255]. Если они из него вылетают, то придётся вручную привести их к этому диапазону.
Зигзаг
После квантования алгоритм JPEG использует зигзаг-сканирование для преобразования матрицы к одномерному виду:
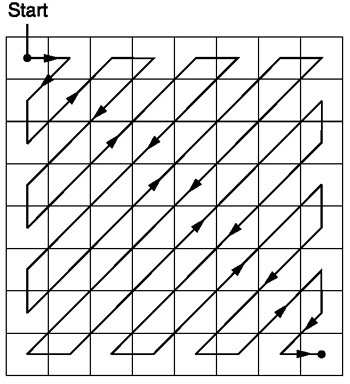
Источник.
Пусть у нас такая квантованная матрица:
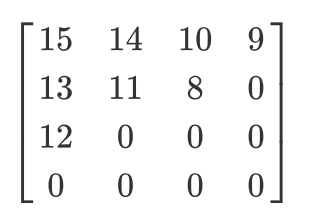
Тогда результат зигзаг-сканирование будет таким:
[15 14 13 12 11 10 9 8 0 ... 0]
Это кодирование является предпочтительным, потому что после квантования большая часть низкочастотной (самой важной) информации будет расположено в начале матрицы, а зигзаг-сканирование сохраняет эти данные в начале одномерной матрицы. Это полезно для следующего этапа — сжатия.
Кодирование длин серий и дельта-кодирование
Кодирование длин серий используется для сжатия повторяющихся данных. После зигзаг-сканирования мы видим, что в конце массива по большей части находятся нули. Кодирование длин позволяет с пользой задействовать это впустую занимаемое пространство и использовать меньше байтов для представления всех этих нулей. Допустим, у нас такие данные:
10 10 10 10 10 10 10
После кодирования длин серий получим вот что:
7 10
Мы сжали 7 байтов в 2 байта.
Дельта-кодирование используется для представления байта относительно байта до него. Проще будет объяснить на примере. Пусть у нас такие данные:
10 11 12 13 10 9
С помощью дельта-кодирования их можно представить так:
10 1 2 3 0 -1
В JPEG каждое DC-значение ДКП-матрицы задаётся с помощью дельта-кодирования относительно предыдущего DC-значения. Это означает, что изменив самый первый ДКП-коэффициент изображения вы порушите всю картинку. Но если если изменить первое значение последней ДКП-матрицы, то это повлияет лишь на очень маленький фрагмент изображения.
Такой подход полезен, потому что первое DC-значение изображения обычно варьируется сильнее всего, и с помощью дельта-кодирования мы приводим остальные DC-значения ближе к 0, что улучшает сжатие с помощью кодирования Хаффмана.
Кодирование Хаффмана
Это метод сжатия информации без потерь. Однажды Хаффман задался вопросом: «Какое наименьшее количество битов я могу использовать для хранения произвольного текста?». В результате был создан формат кодирования. Допустим, у нас есть текст:
a b c d e
Обычно каждый символ занимает один байт пространства:
a: 01100001
b: 01100010
c: 01100011
d: 01100100
e: 01100101
Это принцип двоичной кодировки ASCII. А если нам изменить сопоставление?
# Mapping
000: 01100001
001: 01100010
010: 01100011
100: 01100100
011: 01100101
Теперь нам нужно гораздо меньше битов для хранения того же текста:
a: 000
b: 001
c: 010
d: 100
e: 011
Всё это хорошо, но что если нам нужно ещё сильнее сэкономить пространство? Например, так:
# Mapping
0: 01100001
1: 01100010
00: 01100011
01: 01100100
10: 01100101
a: 0
b: 1
c: 00
d: 01
e: 10
Кодирование Хаффмана позволяет использовать такое сопоставление переменной длины. Берутся входные данные, чаще всего встречающиеся символы сопоставляются с более маленьким сочетанием битов, а менее частые символы — с более крупными сочетаниями. А затем получившееся сопоставления собираются в двоичное дерево. В JPEG мы сохраняем ДКП-информацию с помощью кодирования Хаффмана. Помните, я упоминал, что дельта-кодирование DC-значений облегчает кодирование Хаффмана? Надеюсь, вы теперь понимаете, почему. После дельта-кодирования нам нужно сопоставить меньше «символов» и размер дерева уменьшается.
У Тома Скотта есть прекрасное видео, поясняющее работу алгоритма Хаффмана. Посмотрите, прежде чем читать дальше.
В JPEG содержится до четырёх таблиц Хаффмана, которые хранятся в разделе «Define Huffman Table» (начинается с 0xffc4). ДКП-коэффициенты хранятся в двух разных таблицах Хаффмана: в одной DC-значения из зигзаг-таблиц, в другой — АС-значения из зигзаг-таблиц. Это означает, что при кодировании нам нужно объединить DC- и АС-значения из двух матриц. ДКП-информация для каналов яркости и хроматичности хранится отдельно, так что у нас два набора DC- и два набора AC-информации, в сумме 4 таблицы Хаффмана.
Если изображение представлено в оттенках серого, то у нас только две таблицы Хаффмана (одна для DC и одна для AC), потому что нам не нужен цвет. Как вы уже могли понять, два разных изображения могут иметь очень разные таблицы Хаффмана, поэтому важно хранить их внутри каждого JPEG.
Теперь мы знаем основное содержимое JPEG-изображений. Переходим к декодированию.
Декодирование JPEG
Декодирование можно разделить на этапы:
- Извлечение таблиц Хаффмана и декодирование битов.
- Извлечение ДКП-коэффициентов с помощью отката кодирования длин серий и дельта-кодирования.
- Использование ДКП-коэффициентов для комбинирования косинусных волн и восстановления пиксельных значений для каждого блока 8×8.
- Преобразование YCbCr в RGB для каждого пикселя.
- Отображение получившегося RGB-изображения.
Стандарт JPEG поддерживает четыре формата сжатия:
- Базовый
- Расширенный последовательный
- Прогрессивный
- Без потерь
Мы будем работать с базовым сжатием. Оно содержит серию блоков 8×8, идущих друг за другом. В других форматах шаблон данных немного отличается. Чтобы было понятно, я раскрасил разные сегменты шестнадцатеричного содержимого нашей картинки:
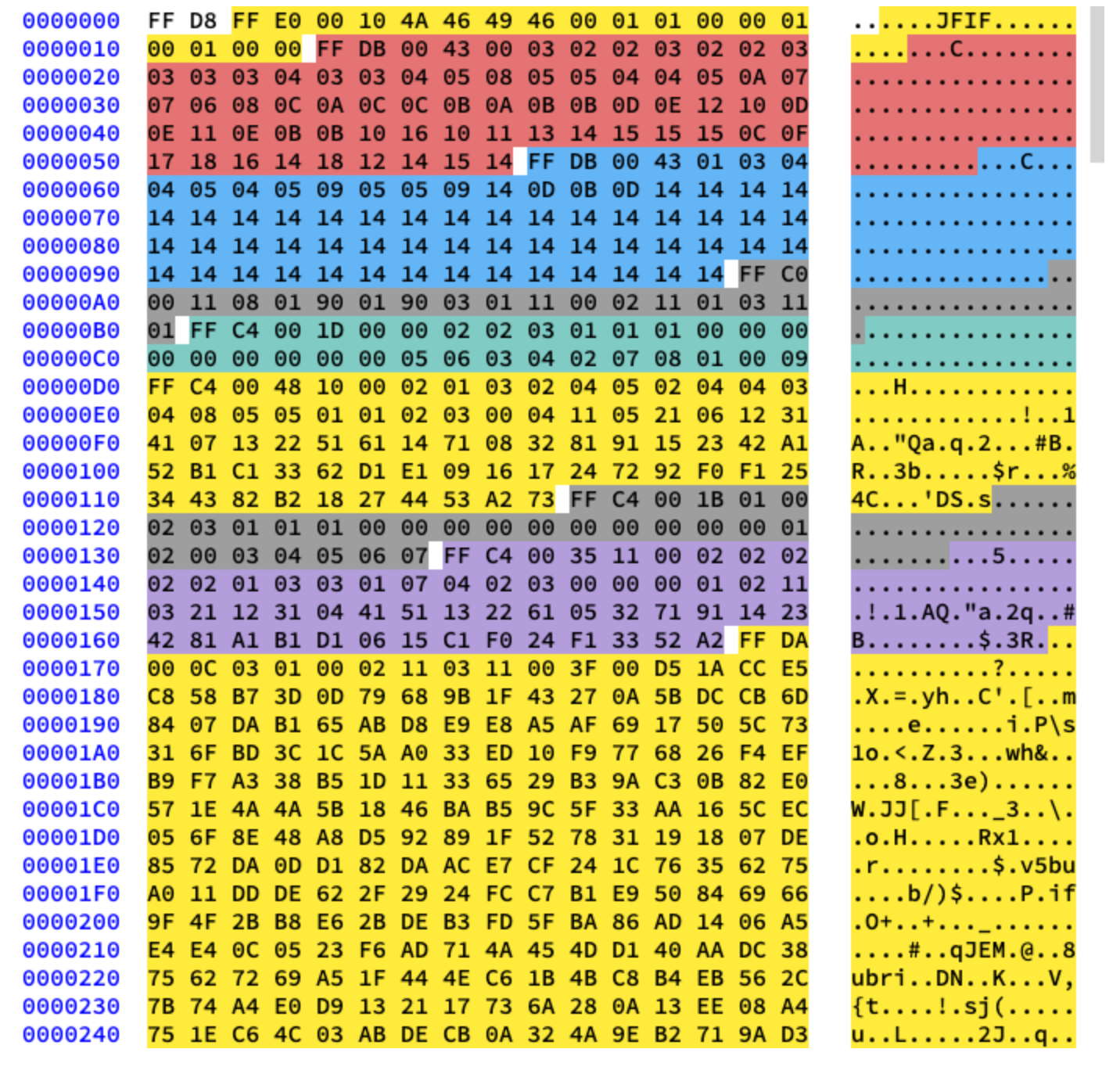
Извлечение таблиц Хаффмана
Мы уже знаем, что JPEG содержит четыре таблицы Хаффмана. Это последний кодирования, поэтому декодировать мы начнём с него. В каждом разделе с таблицей содержится информация:
Допустим, у нас такая таблица Хаффмана (источник):
Она будет храниться в JFIF-файле примерно в таком виде (в двоичном формате. Я использую ASCII только для наглядности):
0 1 5 1 1 1 1 1 1 0 0 0 0 0 0 0 a b c d e f g h i j k l
0 означает, что у нас нет кода Хаффмана длиной 1. А 1 означает, что у нас один код Хаффмана длиной 2, и т.д. В DHT-разделе сразу после класса и ID данные всегда длиной 16 байтов. Напишем код для извлечения длин и элементов из DHT.
class JPEG:
# ...
def decodeHuffman(self, data):
offset = 0
header, = unpack("B",data[offset:offset+1])
offset += 1
# Extract the 16 bytes containing length data
lengths = unpack("BBBBBBBBBBBBBBBB", data[offset:offset+16])
offset += 16
# Extract the elements after the initial 16 bytes
elements = []
for i in lengths:
elements += (unpack("B"*i, data[offset:offset+i]))
offset += i
print("Header: ",header)
print("lengths: ", lengths)
print("Elements: ", len(elements))
data = data[offset:]
def decode(self):
data = self.img_data
while(True):
# ---
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Выполнив код, получим вот что:
Start of Image
Application Default Header
Quantization Table
Quantization Table
Start of Frame
Huffman Table
Header: 0
lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 10
Huffman Table
Header: 16
lengths: (0, 2, 1, 3, 2, 4, 5, 2, 4, 4, 3, 4, 8, 5, 5, 1)
Elements: 53
Huffman Table
Header: 1
lengths: (0, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 8
Huffman Table
Header: 17
lengths: (0, 2, 2, 2, 2, 2, 1, 3, 3, 1, 7, 4, 2, 3, 0, 0)
Elements: 34
Start of Scan
End of Image
Отлично! У нас есть длины и элементы. Теперь нужно создать свой класс таблицы Хаффмана, чтобы восстановить двоичное дерево из полученных длин и элементов. Я просто скопирую код отсюда:
class HuffmanTable:
def __init__(self):
self.root=[]
self.elements = []
def BitsFromLengths(self, root, element, pos):
if isinstance(root,list):
if pos==0:
if len(root)<2:
root.append(element)
return True
return False
for i in [0,1]:
if len(root) == i:
root.append([])
if self.BitsFromLengths(root[i], element, pos-1) == True:
return True
return False
def GetHuffmanBits(self, lengths, elements):
self.elements = elements
ii = 0
for i in range(len(lengths)):
for j in range(lengths[i]):
self.BitsFromLengths(self.root, elements[ii], i)
ii+=1
def Find(self,st):
r = self.root
while isinstance(r, list):
r=r[st.GetBit()]
return r
def GetCode(self, st):
while(True):
res = self.Find(st)
if res == 0:
return 0
elif ( res != -1):
return res
class JPEG:
# -----
def decodeHuffman(self, data):
# ----
hf = HuffmanTable()
hf.GetHuffmanBits(lengths, elements)
data = data[offset:]
GetHuffmanBits берёт длины и элементы, проходит по элементам и кладёт их в список root. Он представляет собой двоичное дерево и содержит вложенные списки. Можете почитать в интернете, как работает дерево Хаффмана и как создать такую структуру данных на Python. Для нашего первого DHT (из картинки в начале статьи) у нас есть такие данные, длины и элементы:
Hex Data: 00 02 02 03 01 01 01 00 00 00 00 00 00 00 00 00
Lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: [5, 6, 3, 4, 2, 7, 8, 1, 0, 9]
После вызова GetHuffmanBits список root будет содержать такие данные:
[[5, 6], [[3, 4], [[2, 7], [8, [1, [0, [9]]]]]]]
HuffmanTable также содержит метод GetCode, который проходит по дереву и с помощью таблицы Хаффмана возвращает декодированные биты. На вход метод получает битовый поток — просто двоичное представление данных. Например, битовым потоком для abc будет 011000010110001001100011. Сначала мы преобразуем каждый символ в его ASCII-код, который преобразуем в двоичный код. Давайте создадим класс, который поможет преобразовать строку в биты, а затем считаем биты один за другим:
class Stream:
def __init__(self, data):
self.data= data
self.pos = 0
def GetBit(self):
b = self.data[self.pos >> 3]
s = 7-(self.pos & 0x7)
self.pos+=1
return (b >> s) & 1
def GetBitN(self, l):
val = 0
for i in range(l):
val = val*2 + self.GetBit()
return val
При инициализации мы даём классу двоичные данные, а затем считываем их с помощью GetBit и GetBitN.
Декодирование таблицы квантования
Раздел Define Quantization Table содержит такие данные:
Согласно стандарту JPEG, в JPEG-изображении по умолчанию есть две таблицы квантования: для яркости и хроматичности. Они начинаются с маркера 0xffdb. Результат работы нашего кода уже содержит два таких маркера. Давайте добавим возможность декодирования таблиц квантования:
def GetArray(type,l, length):
s = ""
for i in range(length):
s =s+type
return list(unpack(s,l[:length]))
class JPEG:
# ------
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
with open(image_file, 'rb') as f:
self.img_data = f.read()
def DefineQuantizationTables(self, data):
hdr, = unpack("B",data[0:1])
self.quant[hdr] = GetArray("B", data[1:1+64],64)
data = data[65:]
def decodeHuffman(self, data):
# ------
for i in lengths:
elements += (GetArray("B", data[off:off+i], i))
offset += i
# ------
def decode(self):
# ------
while(True):
# ----
else:
# -----
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Сначала мы определили метод GetArray. Это лишь удобный метод для декодирования переменного количества байтов из двоичных данных. Также мы заменили часть кода в методе decodeHuffman, чтобы воспользоваться новой функцией. Затем определили метод DefineQuantizationTables: она считывает заголовок раздела с таблицами квантования, а затем применяет данные квантования к словарю, используя в качестве ключа значение заголовка. это значение может быть равно 0 для яркости и 1 для хроматичности. Каждый раздел с таблицами квантования в JFIF содержит 64 байта данных (для матрицы квантования 8×8).
Если вывести матрицы квантования для нашей картинки, то получим вот что:
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
3 2 2 3 2 2 3 3
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
Декодирование начала кадра
Раздел Start of Frame содержит такую информацию (источник):
Здесь нам интересно не всё. Мы извлечём ширину и высоту картинки, а также количество таблиц квантования для каждого компонента. Ширину и высоту будем использовать для начала декодирования фактических сканов изображения из раздела Start of Scan. Поскольку мы будем работать по большей части с YCbCr-изображением, то можно предположить, что компонентов будет три, а их типы будут 1, 2 и 3 соответственно. Напишем код для декодирования этих данных:
class JPEG:
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
self.quantMapping = []
with open(image_file, 'rb') as f:
self.img_data = f.read()
# ----
def BaselineDCT(self, data):
hdr, self.height, self.width, components = unpack(">BHHB",data[0:6])
print("size %ix%i" % (self.width, self.height))
for i in range(components):
id, samp, QtbId = unpack("BBB",data[6+i*3:9+i*3])
self.quantMapping.append(QtbId)
def decode(self):
# ----
while(True):
# -----
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
data = data[len_chunk:]
if len(data)==0:
break
Мы добавили в JPEG-класс атрибут списка quantMapping и определили метод BaselineDCT, который декодирует требуемые данные из SOF-раздела и кладёт количество таблиц квантования для каждого компонента в список quantMapping. Мы воспользуемся этим, когда начнём считывать раздел Start of Scan. Так для нашей картинки выглядит quantMapping:
Quant mapping: [0, 1, 1]
Декодирование Start of Scan
Это «мяско» JPEG-изображения, оно содержит данные самой картинки. Мы дошли до самого важного этапа. Всё, что мы декодировали до этого, можно считать картой, которая помогает нам расшифровать само изображение. В этом разделе содержится сама картинка (в закодированном виде). Мы считаем раздел и расшифруем с помощью уже декодированных данных.
Все маркеры начинались с 0xff. Это значение также может быть частью скана изображения, но если оно присутствует в этом разделе, то после него всегда будет идти и 0x00. JPEG-кодировщик вставляет его автоматически, это называется «вставка байтов» (byte stuffing). Поэтому декодер должен удалять эти 0x00. Начнём с декодирующего SOS метода, содержащего такую функцию, и избавимся от имеющихся 0x00. В нашей картинке в разделе со сканом нет 0xff, но это всё равно полезное дополнение.
def RemoveFF00(data):
datapro = []
i = 0
while(True):
b,bnext = unpack("BB",data[i:i+2])
if (b == 0xff):
if (bnext != 0):
break
datapro.append(data[i])
i+=2
else:
datapro.append(data[i])
i+=1
return datapro,i
class JPEG:
# ----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
return lenchunk+hdrlen
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
elif marker == 0xffda:
len_chunk = self.StartOfScan(data, len_chunk)
data = data[len_chunk:]
if len(data)==0:
break
Раньше мы вручную искали конец файла, когда обнаруживали маркер 0xffda, но теперь, когда у нас есть инструмент, позволяющий систематически просматривать весь файл, перенесём условие поиска маркера внутрь оператора else. Функция RemoveFF00 просто прерывается, когда находит что-то иное вместо 0x00 после 0xff. Цикл прерывается, когда функция находит 0xffd9, и поэтому мы можем искать конец файла, не опасаясь сюрпризов. Если запустите этот код, то в терминале не увидите ничего нового.
Как вы помните, JPEG разбивает изображение на матрицы 8×8. Теперь нам нужно преобразовать данные скана изображения в битовый поток и обработать его по фрагментам 8×8. Добавим код в наш класс:
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk +hdrlen
Начнём с преобразования данных в битовый поток. Вы помните, что к DC-элементу матрицы квантования (её первому элементу) применяется дельта-кодирование относительно предыдущего DC-элемента? Поэтому инициализируем oldlumdccoeff, oldCbdccoeff и oldCrdccoeff с нулевыми значениями, они помогут нам отслеживать значение предыдущих DC-элементов, а 0 будет задан по умолчанию, когда мы найдём первый DC-элемент.
Цикл for может показаться странным. self.height//8 говорит нам, сколько раз мы можем поделить высоту на 8 8, и то же самое с шириной и self.width//8.
BuildMatrix возьмёт таблицу квантования и добавит параметры, создаст матрицу обратного дискретного косинусного преобразования и даст нам матрицы Y, Cr и Cb. А функция DrawMatrix преобразует их в RGB.
Сначала создадим класс IDCT, а затем начнём наполнять метод BuildMatrix.
import math
class IDCT:
"""
An inverse Discrete Cosine Transformation Class
"""
def __init__(self):
self.base = [0] * 64
self.zigzag = [
[0, 1, 5, 6, 14, 15, 27, 28],
[2, 4, 7, 13, 16, 26, 29, 42],
[3, 8, 12, 17, 25, 30, 41, 43],
[9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
]
self.idct_precision = 8
self.idct_table = [
[
(self.NormCoeff(u) * math.cos(((2.0 * x + 1.0) * u * math.pi) / 16.0))
for x in range(self.idct_precision)
]
for u in range(self.idct_precision)
]
def NormCoeff(self, n):
if n == 0:
return 1.0 / math.sqrt(2.0)
else:
return 1.0
def rearrange_using_zigzag(self):
for x in range(8):
for y in range(8):
self.zigzag[x][y] = self.base[self.zigzag[x][y]]
return self.zigzag
def perform_IDCT(self):
out = [list(range(8)) for i in range(8)]
for x in range(8):
for y in range(8):
local_sum = 0
for u in range(self.idct_precision):
for v in range(self.idct_precision):
local_sum += (
self.zigzag[v][u]
* self.idct_table[u][x]
* self.idct_table[v][y]
)
out[y][x] = local_sum // 4
self.base = out
Разберём класс IDCT. Когда мы извлекаем MCU, он будет храниться в атрибуте base. Затем преобразуем матрицу MCU, откатив зигзаг-сканирование с помощью метода rearrange_using_zigzag. Наконец, мы откатим дискретное косинусное преобразование, вызвав метод perform_IDCT.
Как вы помните, ДК-таблица фиксирована. Мы не будем рассматривать, как работает ДКП, это больше относится к математике, чем программированию. Мы можем хранить эту таблицу в виде глобальной переменной и запрашивать для пар значений x,y. Я решил поместить таблицу и её вычисление в класс IDCT, чтобы текст был удобочитаемым. Каждый элемент преобразованной матрицы MCU умножается на значение idc_variable, и мы получаем значения Y, Cr и Cb.
Это будет понятнее, когда мы допишем метод BuildMatrix.
Если вы модифицируете зигзаг-таблицу в подобный вид:
[[ 0, 1, 5, 6, 14, 15, 27, 28],
[ 2, 4, 7, 13, 16, 26, 29, 42],
[ 3, 8, 12, 17, 25, 30, 41, 43],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
[ 9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54]]
то получите такой результат (обратите внимание на маленькие артефакты):

А если наберётесь храбрости, то можете ещё больше модифицировать зигзаг-таблицу:
[[12, 19, 26, 33, 40, 48, 41, 34,],
[27, 20, 13, 6, 7, 14, 21, 28,],
[ 0, 1, 8, 16, 9, 2, 3, 10,],
[17, 24, 32, 25, 18, 11, 4, 5,],
[35, 42, 49, 56, 57, 50, 43, 36,],
[29, 22, 15, 23, 30, 37, 44, 51,],
[58, 59, 52, 45, 38, 31, 39, 46,],
[53, 60, 61, 54, 47, 55, 62, 63]]
Тогда результат будет таким:

Завершим наш метод BuildMatrix:
def DecodeNumber(code, bits):
l = 2**(code-1)
if bits>=l:
return bits
else:
return bits-(2*l-1)
class JPEG:
# -----
def BuildMatrix(self, st, idx, quant, olddccoeff):
i = IDCT()
code = self.huffman_tables[0 + idx].GetCode(st)
bits = st.GetBitN(code)
dccoeff = DecodeNumber(code, bits) + olddccoeff
i.base[0] = (dccoeff) * quant[0]
l = 1
while l < 64:
code = self.huffman_tables[16 + idx].GetCode(st)
if code == 0:
break
# The first part of the AC quantization table
# is the number of leading zeros
if code > 15:
l += code >> 4
code = code & 0x0F
bits = st.GetBitN(code)
if l < 64:
coeff = DecodeNumber(code, bits)
i.base[l] = coeff * quant[l]
l += 1
i.rearrange_using_zigzag()
i.perform_IDCT()
return i, dccoeff
Мы начинаем с создания класса инвертирования дискретной косинусной трансформации (IDCT()). Затем считываем данные в битовый поток и декодируем с помощью таблицы Хаффмана.
self.huffman_tables[0] и self.huffman_tables[1] ссылаются на DC-таблицы для яркости и хроматичности соответственно, а self.huffman_tables[16] и self.huffman_tables[17] ссылаются на AC-таблицы для яркости и хроматичности соответственно.
После декодирования битового потока мы с помощью функции DecodeNumber извлекаем новый дельта-кодированный DC-коэффициент и добавляем к нему olddccoefficient, чтобы получить дельта-декодированный DC-коэффициент.
Затем повторим ту же процедуру декодирования с AC-значениями в матрице квантования. Значение кода 0 говорит о том, что мы дошли до маркера окончания блока (End of Block, EOB) и должны остановиться. Более того, первая часть АС-таблицы квантования говорит нам, сколько у нас начальных нулей. Теперь вспоминаем про кодирование длин серий. Обратим этот процесс вспять и пропустим все эти многочисленные биты. В классе IDCT им явно присваиваются нули.
Декодировав DC- и АС-значения для MCU, мы преобразуем MCU и инвертируем зигзаг-сканирование, вызвав rearrange_using_zigzag. А затем инвертируем ДКП и применительно к декодированным MCU.
Метод BuildMatrix вернёт инвертированную ДКП-матрицу и значение DC-коэффициента. Помните, что это будет матрица только для одной минимальной единицы кодирования размером 8×8. Проделаем это для всех остальных MCU нашего файла.
Вывод изображения на экран
Теперь сделаем так, чтобы наш код в методе StartOfScan создавал Tkinter Canvas и рисовал каждый MCU после декодирования.
def Clamp(col):
col = 255 if col>255 else col
col = 0 if col<0 else col
return int(col)
def ColorConversion(Y, Cr, Cb):
R = Cr*(2-2*.299) + Y
B = Cb*(2-2*.114) + Y
G = (Y - .114*B - .299*R)/.587
return (Clamp(R+128),Clamp(G+128),Clamp(B+128) )
def DrawMatrix(x, y, matL, matCb, matCr):
for yy in range(8):
for xx in range(8):
c = "#%02x%02x%02x" % ColorConversion(
matL[yy][xx], matCb[yy][xx], matCr[yy][xx]
)
x1, y1 = (x * 8 + xx) * 2, (y * 8 + yy) * 2
x2, y2 = (x * 8 + (xx + 1)) * 2, (y * 8 + (yy + 1)) * 2
w.create_rectangle(x1, y1, x2, y2, fill=c, outline=c)
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk+hdrlen
if __name__ == "__main__":
from tkinter import *
master = Tk()
w = Canvas(master, width=1600, height=600)
w.pack()
img = JPEG('profile.jpg')
img.decode()
mainloop()
Начнём с функций ColorConversion и Clamp. ColorConversion принимает значения Y, Cr и Cb, конвертирует их по формуле в RGB-компоненты, а затем выдаёт агрегированные RGB-значения. Вы можете спросить, зачем прибавлять к ним 128? Как вы помните, до алгоритма JPEG к MCU применяется ДКП и вычитает 128 из значений цветов. Если цвета изначально были в диапазоне [0,255], JPEG поместит их в диапазон [-128,+128]. Нам нужно откатить этот эффект при декодировании, и поэтому прибавляем 128 к RGB. Что касается Clamp, то при распаковке получающиеся значения могут выходить за пределы [0,255], поэтому мы удерживаем их в этом диапазоне [0,255].
В методе DrawMatrix мы циклически проходим по ка
