[Перевод] Даты среди цифр числа Пи: некоторые мысли с позиции статистики и нумерологии

Перевод поста Майкла Тротта (Michael Trott) «Dates Everywhere in Pi (e)! Some Statistical and Numerological Musings about the Occurrences of Dates in the Digits of Pi».
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикацииСодержание
Получим все даты за последние 100 лет
Найдём все даты в цифрах числа пи
Статистика всех дат
Первые появления дат
Даты в других представлениях и других константахВ недавнем своём посте (см. перевод поста »3/14/15 9:26:53 Празднование «Дня числа Пи» века, а также рассказ о том, как получить свою очень личную частичку числа пи» на Хабре) Стивен Вольфрам писал об уникальном положении векового дня числа пи и представил разные примеры содержания дат в цифрах числа пи (здесь и далее — в десятичном представлении). В этом посте я рассмотрю статистику распределений всех возможных дат за последние 100 лет в первых 10 миллионах цифр числа пи. Мы увидим, что 99,998% цифр представляют собой какую-то дату, и что можно обнаружить миллионы дат в первых десяти миллионах цифр числа пи.
Я сосредоточусь на датах, которые могут быть заданы не более чем шестью цифрами. То есть я смогу одназначно задавать даты в промежутке длительностью в 36 525 дней, начиная с 15 марта 1915 года и заканчивая 14 марта 2015 года.
Начнём с графической визуализации нашей темы для задания настроения.

Получим все даты за последние 100 лет
Как и обычно, день числа пи в этом году выпал на 14 марта.

С векового дня пи 20 века прошло 36 525 дней.

Создадим список из всех 36 525 рассматриваемых дат.
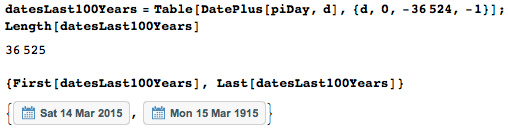
Для дальнейшей работы определим функцию dateNumber, которая для заданной даты возвращает порядковый номер даты, начиная с первой (15 марта 1915 г. имеет номер 1).
Месяцам с сентября по январь я позволю задаваться лишь одной цифрой — то есть 9 для сентября вместо 09; аналогично и для дней. То есть некоторые даты могут быть заданы разными последовательностями цифр. Функция makeDateTuples генерирует все последовательности целых чисел, представляющих даты. Можно использовать несколько различных обозначений дат — всегда с нулями или всегда в короткой записи. С опциональным включением нулей в запись дней и месяцев получится больше возможных соответствий и больше результатов, так что я буду использовать их в дальнейшем. (А если вы предпочитаете обычный формат записи дат в виде день-месяц-год, то тогда нужно будет просто внести изменения в функцию makeDateTuples).
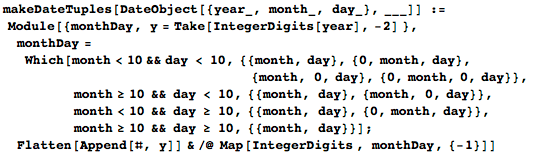
Даты могут быть представлены одним, двумя либо четырьмя способами:
Следующий график показывает то, какие дни прошлого года представимы четырьмя, пятью, и шестью цифрами. Первые девять дней в период с января по сентябрь для записи требуют четыре или пять цифр, а последние дни октября, ноября и декабря требуют шесть.
Для быстрого (за постоянное время) повторяющегося распознавания последовательности как даты я задам функции dateQ и datesOf. datesOf дает нормализованную форму последовательности цифр даты. Начнем с создания пары последовательностей и их интерпретации как дат.

Вот некоторые примеры.
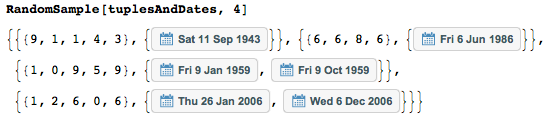
Большинство (77 350) последовательностей могут быть однозначно истолкованы как даты; некоторые (2700) имеют две возможные интерпретации.

Вот некоторые из последовательностей цифр с двумя интерпретациями.

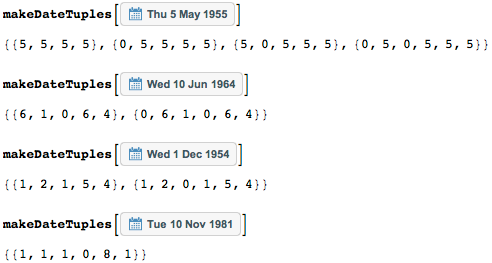
Последовательность {1,2,1,5,4} имеет две интерпретации — как 21 января 1954 или как 1 декабря 1954 — восстановленные с помощью функции datesOf.

Это количества четырех-, пяти-, и шестизначных представлений дат.

А это число определений каждого из типов, установленных для функции datesOf.

Найдём все даты в цифрах числа пи
Для всех дальнейших расчетов я буду использовать первые десять миллионов десятичных цифр числа пи (позже будет показано, что десяти миллионов вполне достаточно, чтобы найти в них любую дату). Мы запросто можем заменить пи на любую другую константу (код универсален).
Вместо того чтобы использовать полную последовательность цифр как строку, я буду использовать последовательность цифр, разделённую на (перекрывающиеся) последовательности. Теперь можно быстро и независимо работать с каждой последовательностью. И я проиндексировал последовательности порядковыми номерами цифр. Например:

Используя определенные выше функции dateQ и datesOf, я могу теперь быстро найти все последовательности цифр, которые могут быть интерпретированы как даты.
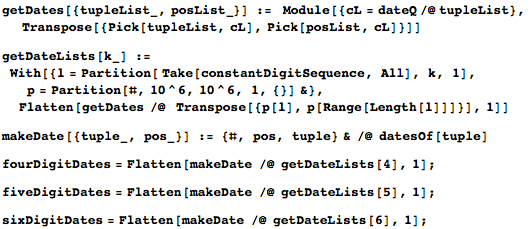
Вот некоторые найденные интерпретации дат. Каждый подсписок имеет вид:
{date, startingDigit, digitSequenceRepresentingTheDate}
(дата, начальная цифра, последовательность цифр представляющих дату).

Мы нашли около 8,1 млн. дат, представленных четырьмя цифрами; около 3,8 млн. дат — пятью; около 365 тыс. дат — шестью, итого в сумме более 12 млн. дат.

Обратите внимание, что я мог бы использовать строковые функции обработки (особенно StringPosition), для поиска позиций последовательностей дат. И, конечно, я бы получил тот же результат.

В то время как использование StringPosition хорошо подошло бы для поиска одной даты, работа же со всеми 35 000 последовательностей заняло бы гораздо больше времени.

Остановимся на секунду и посмотрим на счётчик найденных последовательностей из 4 цифр. Из 10 000 возможных четырёхзначных последовательностей используется 8 100, при этом каждая из них появляется в среднем (1/10)⁴ * 10⁷ = 10⁴ раз, что следует из «случайности» распределения цифр числа пи. Полагаю, стандартное отклонение должно быть около 1000^½≈31.6. Небольшой расчёт и график подтверждают эти цифры.

Кривая распределения количества различных дат из четырёх цифр имеет ожидаемый вид колокола.
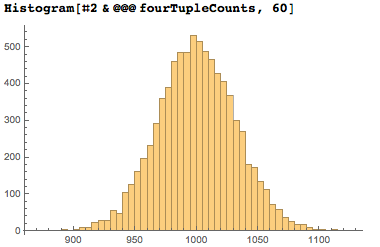
А следующий график показывает то, как часто каждая из 4-значных последовательностей, которая представляет какую-то дату, появляется в первых десяти миллионах цифр числа пи в десятичном представлении. Мы пронумеровали все 4-значные последовательности путём объединения цифр в число; в результате можно увидеть пустые вертикальные полосы в областях, в которых 4-значные последовательности не представляют даты.
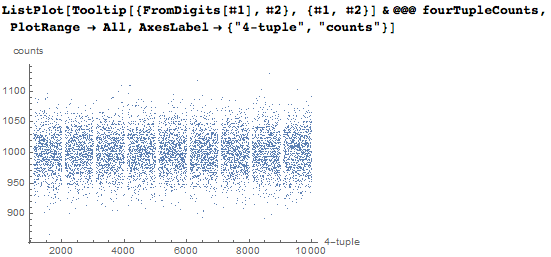
Продолжим теперь обрабатывать найденные позиции дат. Сгруппируем результаты в подсписки из одинаковых дат.

И в самом деле, в первых 10 миллионах цифр встречаются все даты, то есть получается, что найдено 36 525 разных дат (далее мы увидим, что выбор числа цифр для анализа был оптимальным).

Вот как выглядит типичный член dateGroups.
Статистика всех дат
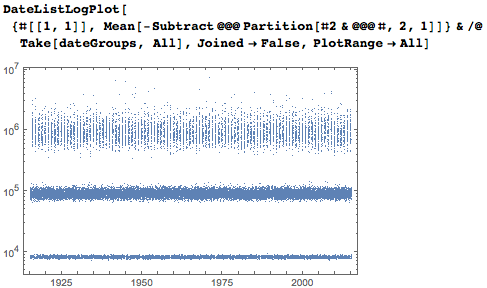
Рассмотрим теперь найденные данные с точки зрения статистики. Вот число вхождений каждой даты в первые десять миллионов цифр числа пи. Интересно, а может быть даже несколько неожиданно, но многие даты встречаются сотни раз. Периодически возникающие вертикальные полосы появляются из-за квартала октябрь-ноябрь-декабрь.

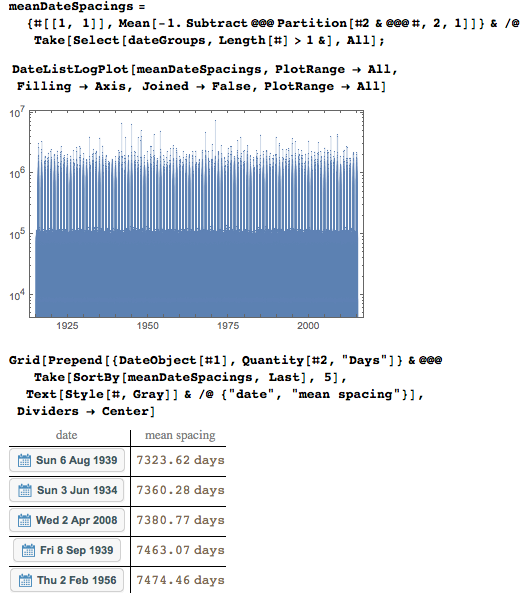
Среднее расстояние между датами также ясно показывает раннее появление четырёхзначных записей годов со средними промежутками менее 10 000, пятизначным соответствуют промежутки около 100 000, шестизначным — около 1 000 000.
Для облегчения читаемости, я отформатировал тройки {date, StartingPosition, dateDigitSequence} индивидуальным образом.
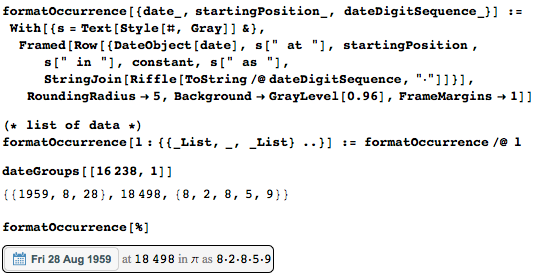
Самая частая дата среди первых 10 миллионах цифр — 6 августа 1939 года — встречается 1 362 раза.

Давайте найдём теперь самые редкие. Вот эти три даты встречаются только по разу.

А эти по два (вывод результата укорочен для экономии места).

Вот распределение числа вхождений дат. Три пика, соответствующих четырёх-, пяти- и шестициферным представлениям дат (слева направо) явно различаются. Даты, которые представляются последовательностями из 6 цифр, возникают нечасто; как было показано выше, появляются в среднем около 1200 раз.

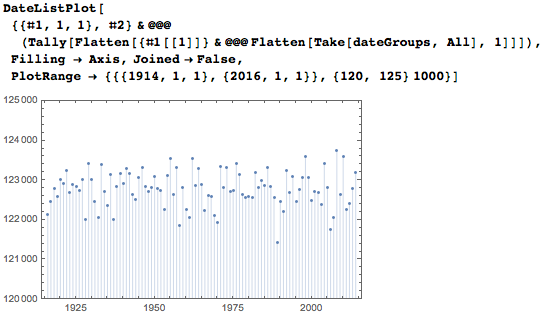
Можно также собирать и отображать даты по годам (меньшие значения в концах появляются из-за усечения дат для обеспечения их уникальности). Распределение практически равномерное.
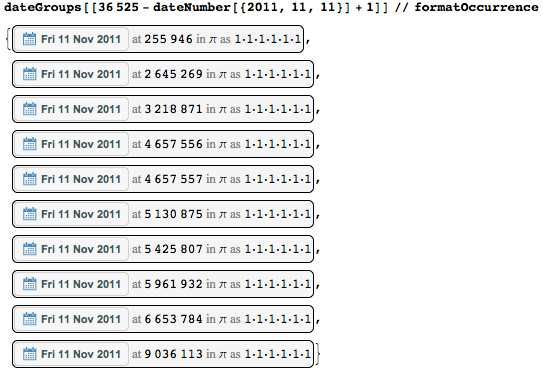
Давайте посмотрим на даты с красивыми последовательностями цифр и на то, как часто они появляются. Так как результаты в dateGroups сортируются по дате, я могу легко получать доступ к указанным датам. Скажем, где располагается дата 11–11–11?
А дата 1–23–45?

Ни одна из дат не начинается на своей собственной позиции (то есть нет примеров наподобие того, что 1 января 1945 [1–1–4–5] находится на позиции 1145).

Но имеется один «палиндромный случай»: 3 марта 1985 (3.3.8.5) лежит на палиндромной позиции 5833.
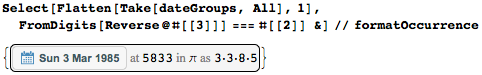
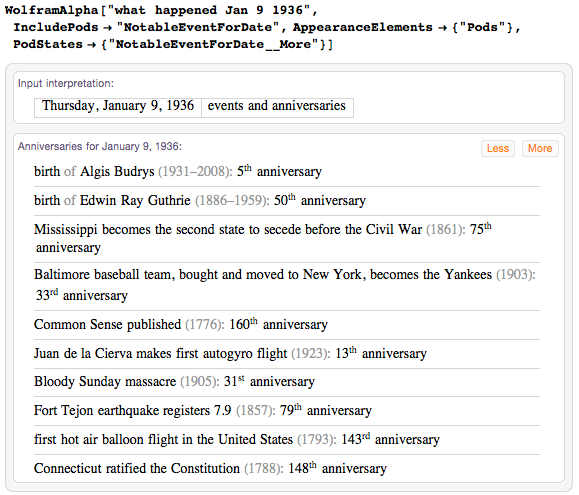
Весьма особая дата — 9 января 1936: она появляется на позиции 1936-го простого числа — 16 747.

Давайте рассмотрим памятные события в этот день в истории.
Так как не было ни одной даты, которая появилась бы на своей позиции, то мы можем смягчить условия и найти все даты, которые «накладываются» на свои позиции.

И более чем 100 раз в первых 10 миллионах цифр числа пи можно встретить известную комбинацию первых цифр числа пи — 314159.

В числе пи можно найти не просто даты дней рождений, но и дни физических констант, такие как ħ-день (день редуцированной постоянной Планка), который, к примеру, отмечался как вековой 5 октября 1945 года.

Вот позиции совпадающих дат.
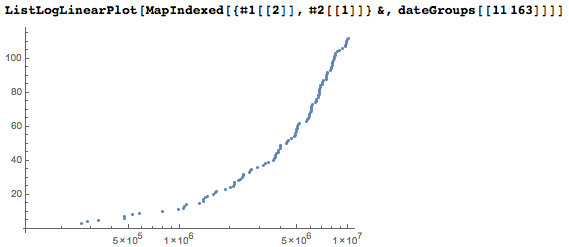
А вот попытка визуализировать встречаемость всех дат. В плоскости даты-цифры зададим точки для начала каждой даты. Мы используем логарифмическую шкалу для позиций цифр, и в результате количество точек значительно больше в верхней части графика.

Для дат, которые рано появляются в цифровой последовательности, конечный объём дат в цифрах также может быть визуализирован. Даты задаются четырьмя-шестью цифрами. Следующий график показывает цифры всех дат, которые начинаются в первых 10 000 цифрах.

После огрубления, распределение становится довольно равномерным.

До сих пор я брал дату и смотрел, с какой позиции она начинается в последовательности цифр числа пи. Давайте теперь поступим наоборот: сколько дат содержат данную цифру числа пи? Чтобы найти общее число дат для каждой цифры, можно пройтись циклом по датам.

Получается до 20 дат на каждую цифру.

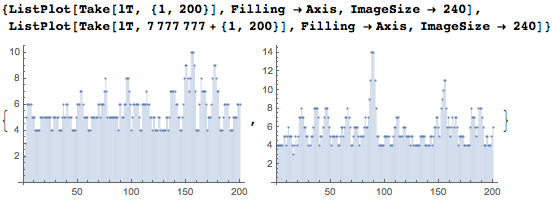
Вот два интервала по 200 цифр каждый. Мы видим, что большинство цифр содержатся в датах.
Выше я отмечал, что у меня в последовательности цифр нашлось около 12 миллионов дат. Последовательность цифр, которую я использовал, имеет длину всего в десять миллионов цифр, а каждая дата содержит около пяти цифр. Это означает, что на все эти даты нужно около 60 миллионов цифр. Из этого следует, что многие из десяти миллионов цифр должны быть многократно использованы — в среднем около пяти раз. Только 2005 из первых десяти миллионов цифр не используются ни в одной из последовательностей, интерпретированных как даты, и это означает, что 99,98% всех цифр используются в датах (не все на первой позиции).

А вот гистограмма распределения числа дат, присутствующих на каждой конкретной цифре. Можно отчётливо увидеть без особых вычислений, что в среднем на одну цифру приходится около 6 дат.

2005 не входящих ни в одну дату цифр довольно равномерно распределены в первых десяти миллионах цифр.
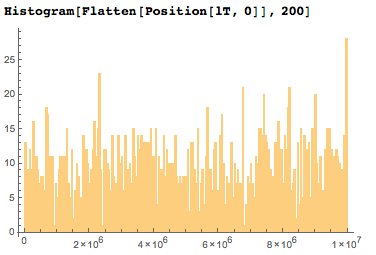
Если я изображу конкретные позиции незадействованых цифр по сравнению с их ожидаемой средней позицией, то я получу нечто наподобие графика случайных блужданий.
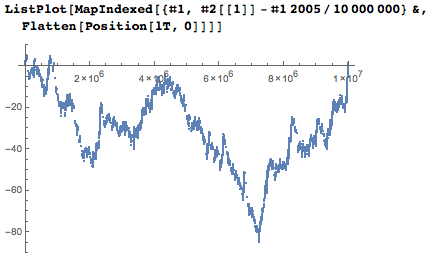
Итак, с кем граничат неиспользованные цифры? Существует 162 различные окрестности из 5 цифр. Глядя на них, сразу видно, почему центральная цифра не может быть частью даты: слишком много нулей в округе.

И самый большой неиспользованный блок цифр — шесть цифр между положениями 8 127 088 и 8 127 093.

В большинстве цифр перекрываются даты разных лет. График ниже показывает диапазон лет от ранних к поздним, как функцию от позиции цифры.
Вот неиспользованные цифры вместе с тремя левыми и тремя правыми соседями.

Для того, чтобы проиллюстрировать работу алгоритма выше, я возьму случайную цифру и найду все даты, которые ее «накрывают».
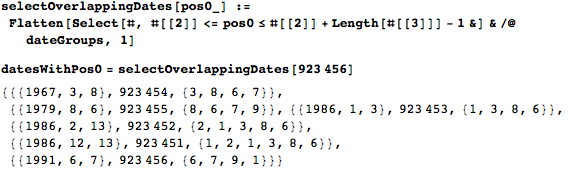
А вот визуализация «наложения» дат.
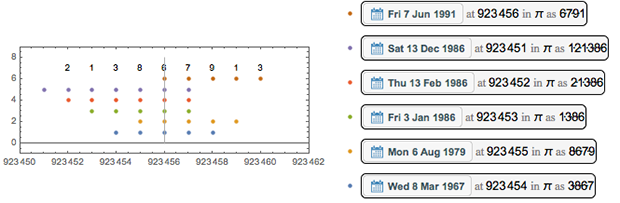
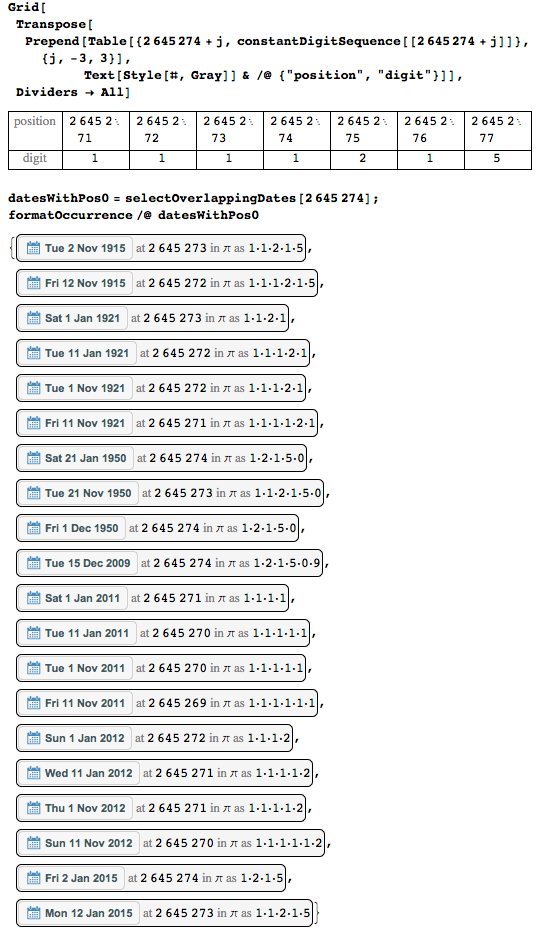
Наиболее используемая цифра — единица на позиции 2 645 274 — она присутствует в 20 различных датах.

Вот цифры в её окрестности и возможные даты.
Если я построю года, начиная с данной цифры для большего количества цифр (скажем, для первых 10 000), то я увижу относительно плотное покрытие дат на плоскости цифры-даты.

Давайте теперь построим график связанных дат. Будем считать две даты связанными, если они имеют хотя бы одну общую цифру (не обязательно начальную).

Ниже показан такой же граф, только для первых 600 цифр, но с выделенными сообществами (community).

Высчитаем теперь среднее расстояние между двумя появлениями одной и той же даты.
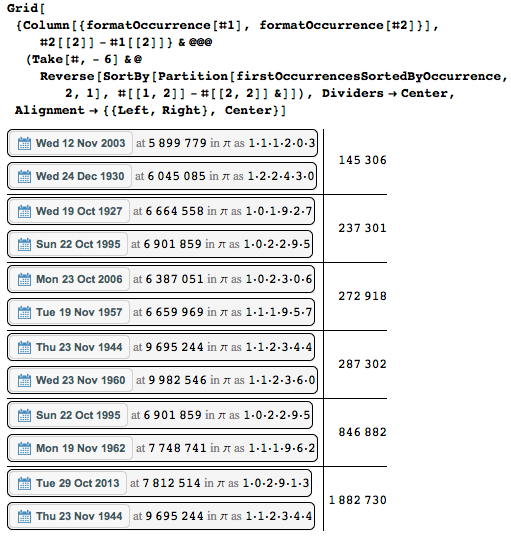
Первые появления дат
Наиболее интересны первые появления дат, так что давайте извлечём их. Мы будем работать с двумя версиями списка дат, первый представляет собой список списков вида {дата, первая позиция даты} (firstOccurrences), а второй — тот же список, отсортированный по номеру позиции в цифрах числа пи (firstOccurrencesSortedByOccurrence).

Все возможные интерпретации дат в первых десяти цифрах числа пи.

Или вот другая крайность — даты, которые встречаются в первый раз как можно позже.
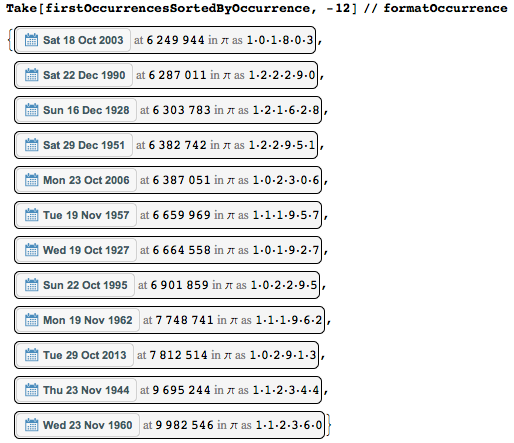
Можно увидеть, что среда 23 ноября 1960 начинается только в положении 9 982 546 (= 2×7*713039) — так, используя лишь первые десять миллионов цифр, мне повезло поймать её. Вот быстрая прямая проверка этой «рекордной» даты.

И кто же те счастливчики из известных людей, кому повезло родиться в этот день?

И в каких фазах была луна во время каждой из топ-10 самых «глубоко зарытых» дат?
И в то время, как среда 23 ноября 1960 — это самая дальняя дата в десятичной последовательности цифр, самая последняя позиция в виде простого числа соответствует дате 22 октября 1995.

В целом получается, что менее 10% всех дат появляются на позициях в виде простых чисел.

Часто некоторые направляют цифры числа пи по определённому направлению на плоскости, формируя случайные блуждания. Мы сделаем то же самое в зависимости от расстояния между первыми появлениями дат. Получим изображения типичных двумерных случайных блужданий.

Вот позиции первых появлений дат за последние несколько лет. Всплески в октябре, ноябре и декабре каждого года вызваны необходимостью задания дат последовательностями из пяти или шести цифр, в то время как с января по сентябрь даты можно задать меньшим количеством цифр, если пропустить необязательные нули.
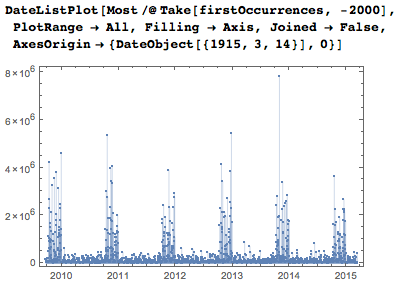
Если я включу все даты, я получу, конечно же, гораздо более «плотные» графики.
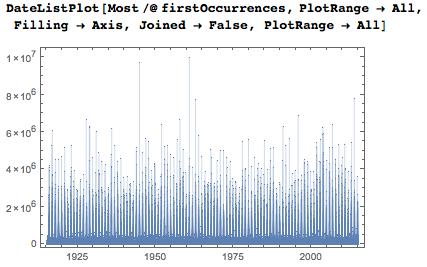
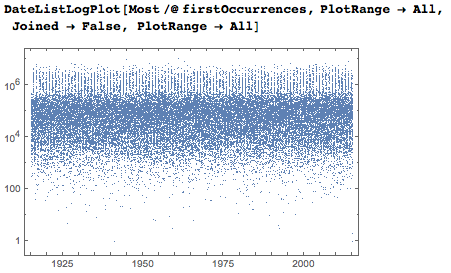
Логарифмическая вертикальная ось показывает, что большинство дат впервые появляются между тысячной и миллионной цифрами.
Чтобы получить более глубокое и интуитивное понимание общей однородности и локальных «случайностей» в последовательности цифр (и, как следствие, в датах), я приведу диаграмму Вороного в плоскости дни-цифры, основанную на точках первых появлений дат. Уменьшение плотности при возрастании номера объясняется тем, что я рассматривал лишь первые появления дат.

Пасхальное воскресенье — отличная дата для визуализации, так как каждый год оно выпадает на разные дни.

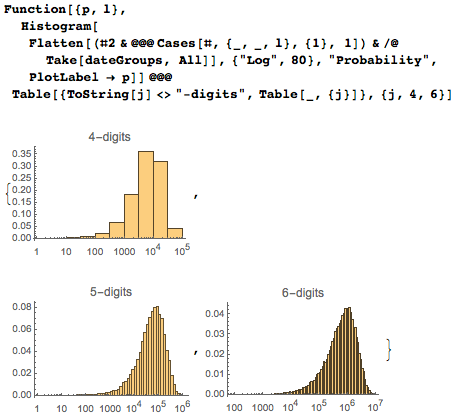
Средняя позиция первого появления даты, как функция от количества цифр, необходимых для её указания зависит, конечно, от количества цифр, необходимых для её кодирования.

Средняя позиция первого появления даты приходится на 239 083, но из-за разброса в несколько миллионов цифр, стандартное отклонение гораздо больше.

Вот первые вхождения «хороших» дат, образованных повторением одной цифры.
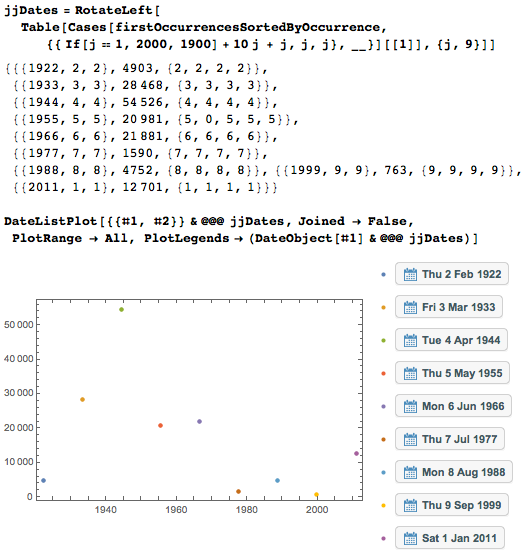
Подробное распределение числа появлений первых дат имеет наибольшую плотность в первых нескольких десятках тысяч цифр.
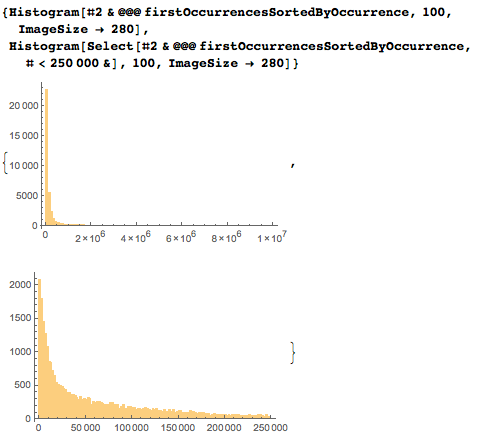
Логарифмические оси гораздо лучше подходят для демонстрации распределения, однако из-за увеличения размеров ячеек следует осторожно подходить к интерпретации максимума.
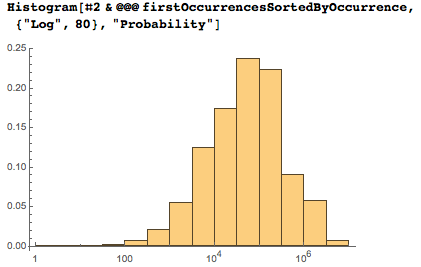
Последнее распределение есть по сути взвешенная суперпозиция из первых появлений четырех-, пяти-, и шестизначных последовательностей.
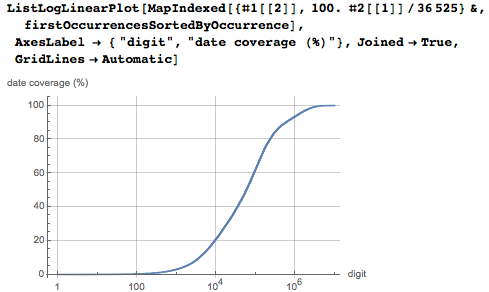
А вот совокупное распределение дат в зависимости от позиции цифры. Можно увидеть, что первый 1% из десяти миллионов цифр содержит уже 60% всех дат.
На чётных позициях дат чуть больше, чем на нечётных.

Можно сделать то же самое для чисел, кратным трём, четырём и так далее. Левое изображение показывает отклонение каждого класса соответствий от среднего значения, а правое — наибольшие соответствия, рассмотренные по критерию чётности.

Фактические количества первых вхождений в каждый определённый год колеблются вокруг среднего значения.
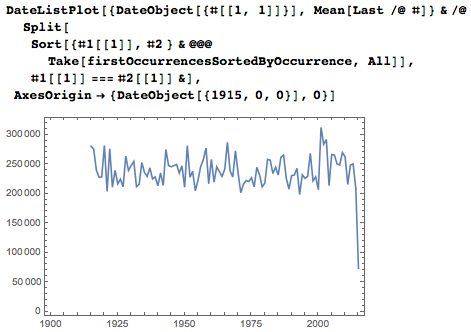
Средние числа первых вхождений дат, отсортированные по месяцам, отчётливо разделяют двузначные и однозначные записи для месяцев.
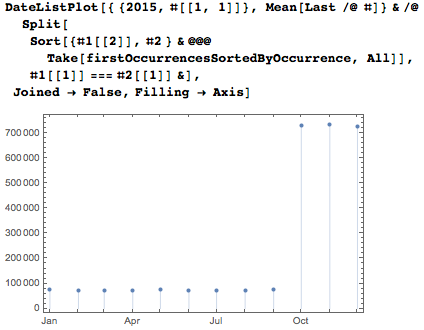
Средние числа по дням месяца (1–31) в основном представляют из себя медленно возрастающие функции.

Наконец, вот средние по дням недели. Большинство первых вхождений для дат приходится на даты, соответствующие среде.

Выше я отмечал, что большинство цифр входят в какие-то даты. Лишь небольшое число цифр содержатся в датах, которые появляются впервые (121 470).

Некоторые из позиций последовательностей в любом случае перекрываются, и я могу сформировать сеть из цепей дат с перекрывающимися последовательностями цифр.

Следующий график показывает возрастающие размеры промежутков между последовательными датами.
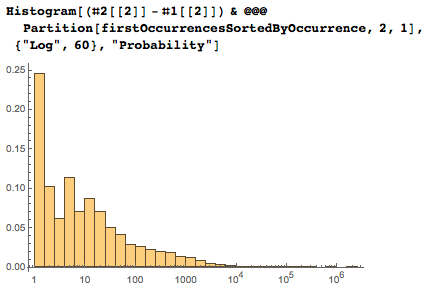
Распределение размеров промежутков:
Вот пары наиболее отдалённых друг от друга последовательных дат. На предпоследнем рисунке отчётливо видны большие промежутки.
Даты в других представлениях и других константах
Теперь рассмотрим особые даты, в которых левые части цепной дроби (числа перед знаком плюс) совпадают с числами в десятичном представлении.

Это дает следующую строку цепной дроби числа пи:

И, что интересно, есть только один такой день.

Ни один из расчетов, проведенных до сих пор не проводились относительно цифр числа пи. Цифры любых других иррациональных чисел (или даже достаточно длинных рациональных чисел) содержат даты. Было занятно найти много числовых выражений, которые содержат даты этого года (2015). Здесь они собраны вместе в интерактивной демонстрации.
Теперь мы подошли к концу наших размышлений. В качестве последнего примера, давайте попробуем проинтерпретировать положения цифр в качестве секунд после времени пи в этом году, которое случилось 14 марта в 9:26:53. Как долго мне придётся ждать появления последовательности цифр 3 • 1 • 4 • 1 • 5 в десятичном представлении других констант? Можно ли найти такое выражение (небольшое), в первый миллион цифр которого не попадает последовательность 3 • 1 • 4 • 1 • 5?(Большинство элементов следующего списка ξs есть случайные выражения. Последние элементы были найдены при поиске выражений, которые имеют последовательность цифр 3 • 1 • 4 • 1 • 5 настолько далеко, насколько это возможно)

Вот два рациональных числа, которые в десятичной записи содержат последовательность цифр:

И вот два целых числа с начальными цифрами числа пи.

Использование новой функции TimelinePlot, которую Brett Champion, описал в его последнем посте в посте (см. пост «Новое в Wolfram Language: функция TimelinePlot для создания временной шкалы » на Хабре), я могу легко показать, как долго мне придется ждать.
Использование аккуратный новую функцию TimelinePlot, что чемпион Бретт, описанной в его последнем сообщении в блоге, я могу легко показать, как долго мне придется ждать.

Мы призываем читателей провести более глубокое исследование дат в цифрах числа пи, или же рассмотреть вместо пи другую постоянную (например, число e Эйлера), и, возможно даже в другой системе счисления. В целом, качественные структуры будут одинаковыми для почти всех иррациональных чисел (чтобы посмотреть другую картину, попробуйте постоянную Чамперноуна ChampernowneNumber[10]). Будут ли первые десять миллионов цифр числа e содержать все даты? А на какой позиции будет находиться 21 октября 2014? Какие особенные даты содержатся в других константах? Эти и многие другие вопросы, ожидают своих ответов.
