[Перевод] Цвет: от шестнадцатеричных кодов до глаза16.04.2018 15:18

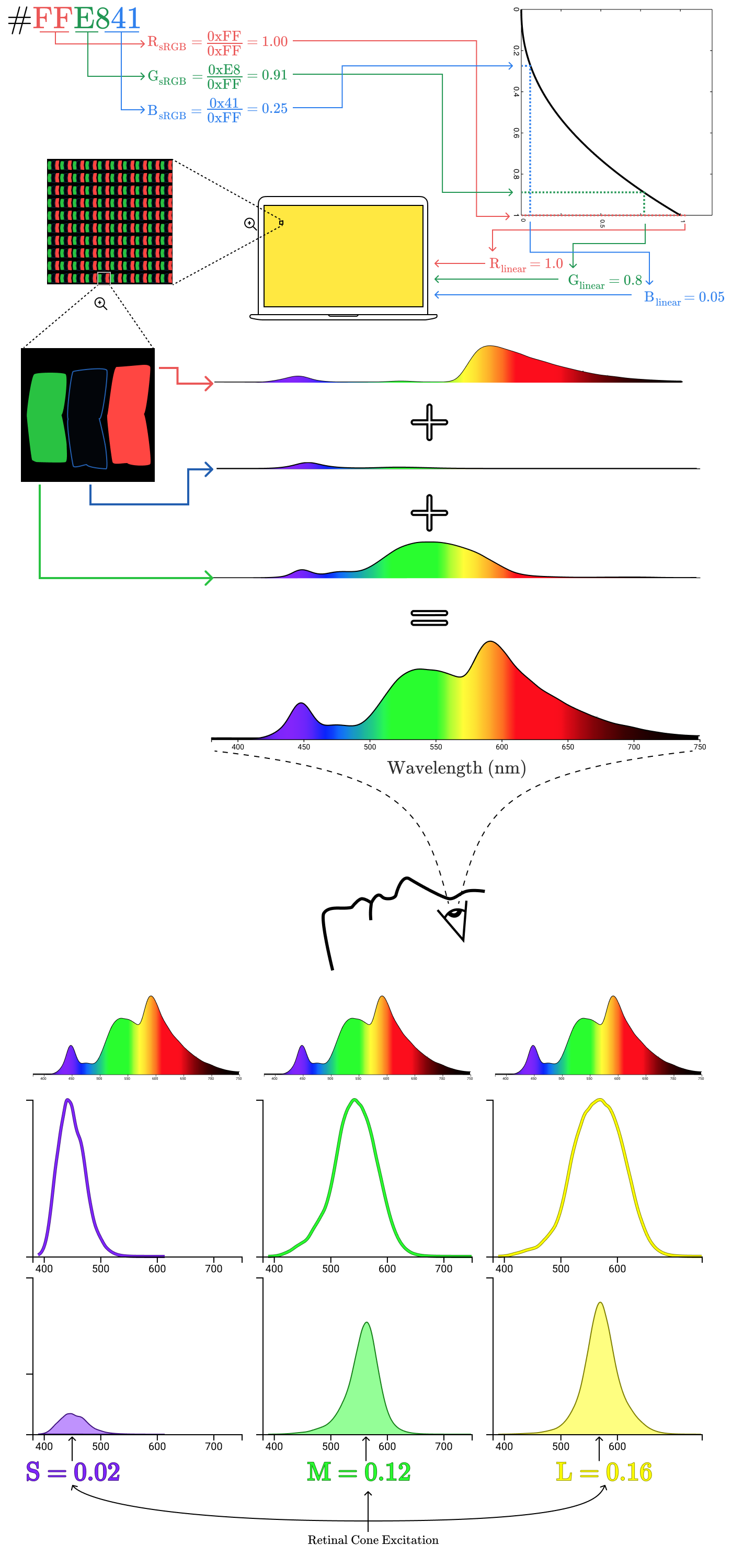
Почему мы воспринимаем background-color: #9B51E0 как этот конкретный фиолетовый цвет?

Долгое время я думал, что знаю ответ на этот вопрос. Но хорошенько поразмыслив, осознал значительные пробелы в своих знаниях.

Сейчас я надеюсь заполнить некоторые из этих пробелов, изучив электромагнитное излучение, оптическую биологию, колориметрию и оборудование для отображения цвета. Если хотите, можно перескочить к определённому разделу, вот оглавление:

Электромагнитное излучение
Видимый свет
Воспринимаемая на глаз яркость
Количественное определение цвета
Оптическая биология
Цветовые пространства
Эксперименты Райта и Гилда по сложению цветов
Визуализация цветовых пространств и хроматичности
Гаммы и спектральный локус
Цветовое пространство CIE XYZ
Субпиксели экрана
sRGB
Шестнадцатеричные коды sRGB
Гамма-коррекция
От шестнадцатеричных кодов до глаза
Краткое примечание о настройке яркости
Вещи, которые я упустил
Ссылки на литературу

В противном случае начнём с физики.

Электромагнитное излучение
Радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолет, рентгеновские лучи и гамма-излучение — всё это формы электромагнитного излучения. Хотя они называются по-разному, но эти названия просто обозначают различные диапазоны длин волн в электромагнитном спектре.

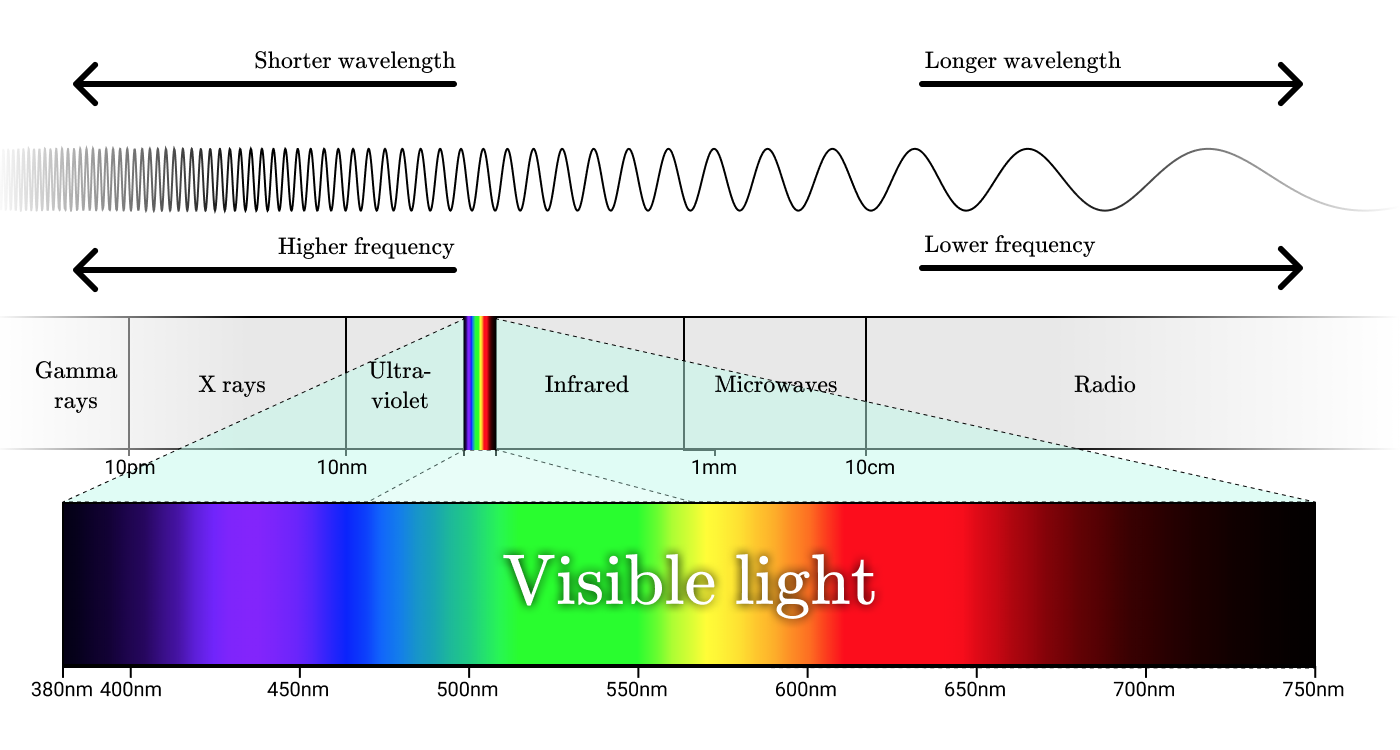
Электромагнитный спектр

Наименьшей единицей электромагнитного излучения является фотон. Энергия фотона пропорциональна частоте соответствующей ему волны, а фотоны высоких энергий соответствуют высокочастотным волнам.

Чтобы понять цвет, нужно сначала понять излучение. Давайте внимательнее посмотрим на излучение лампы накаливания.

Фото: Alex Iby

Мы можем задать вопрос, сколько энергии излучает лампа. Поток излучения ( $\Phi_e$ ) объекта — это общая энергия, излучаемая в секунду, которая измеряется в ваттах. Поток излучения стоваттной лампочки накаливания составляет около 80 Вт, а оставшиеся 20 Вт напрямую преобразуются в неизлучаемое тепло.

Если мы хотим узнать, сколько энергии приходится на каждый волновой диапазон, то можно посмотреть на спектральную плотность излучения. Спектральная плотность излучения ( $\Phi_{e,\lambda}$ ) объекта — это поток излучения на единицу длины волны. Как правило, она измеряется в ваттах/нанометр.

Если изобразить спектральную плотность излучения нашей лампочки накаливания как функцию длины волны, то она будет выглядеть примерно так:

Площадь области, ограниченной этой кривой, соответствует потоку излучения. В виде уравнения: $\Phi_e = \int_0^\infty \Phi_{e,\lambda}(\lambda) d\lambda$ . В данном случае площадь области соответствует примерно 80 Вт.

$\Phi_{e}^{\text{bulb}} = \int_0^\infty \Phi_{e,\lambda}^\text{bulb}(\lambda) d\lambda = 80\text{W}$

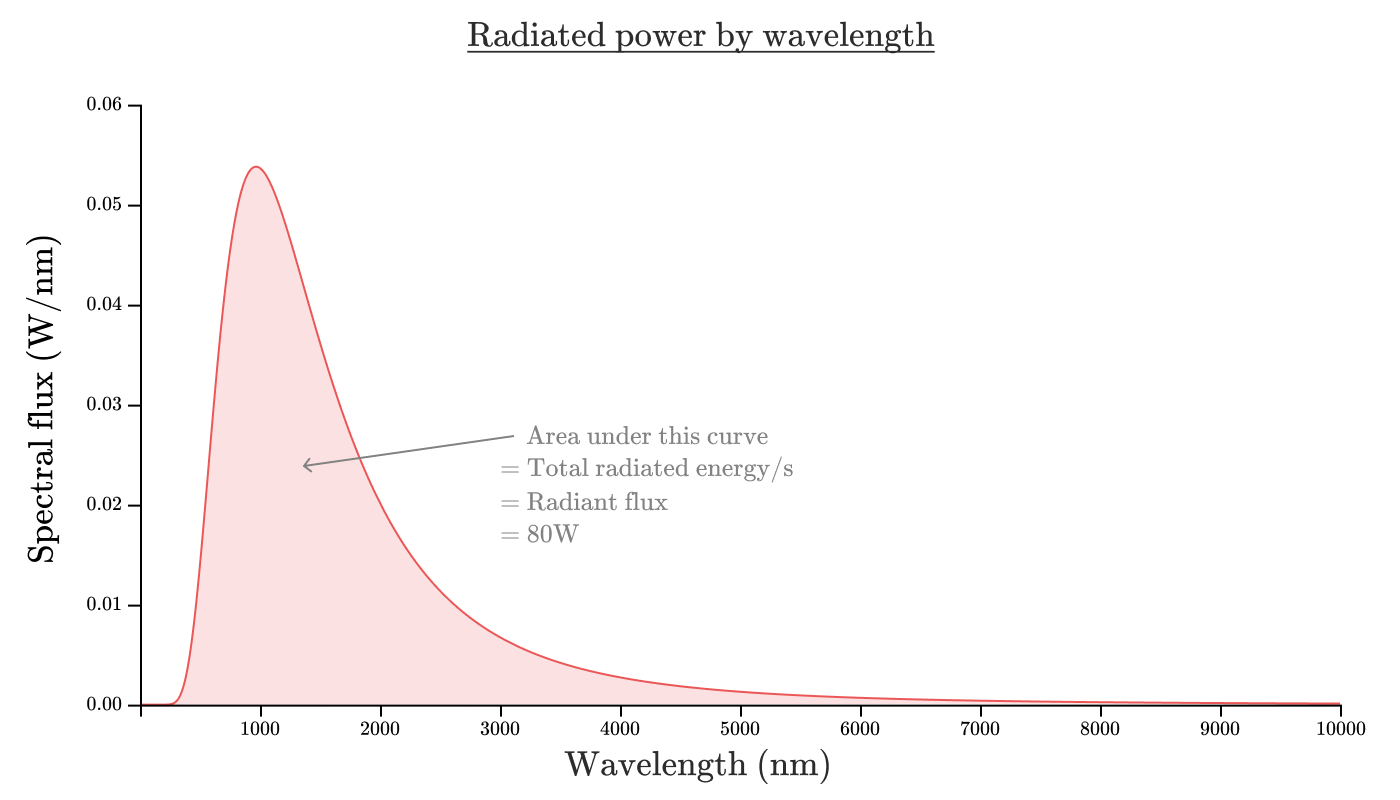
Возможно, вы слышали из рекламы защитников природы, что лампочки накаливания крайне неэффективны и думаете: «Хм, 80% не кажется таким уж плохим КПД».

И это правда. Лампочка накаливания — весьма эффективный способ преобразования электричества в излучение. К сожалению, это ужасный способ преобразования электричества в видимое человеком излучение.

Видимый свет
Видимый свет находится в диапазоне длин волн от $\lambda = 380\text{nm}$ до $\lambda = 750\text{nm}$ . На графике для лампы накаливания это затенённая область, показанная ниже.

$\int_{380 \text{nm}}^{750 \text{nm}} \Phi_{e,\lambda}^\text{bulb}(\lambda) d\lambda = 8.7W$

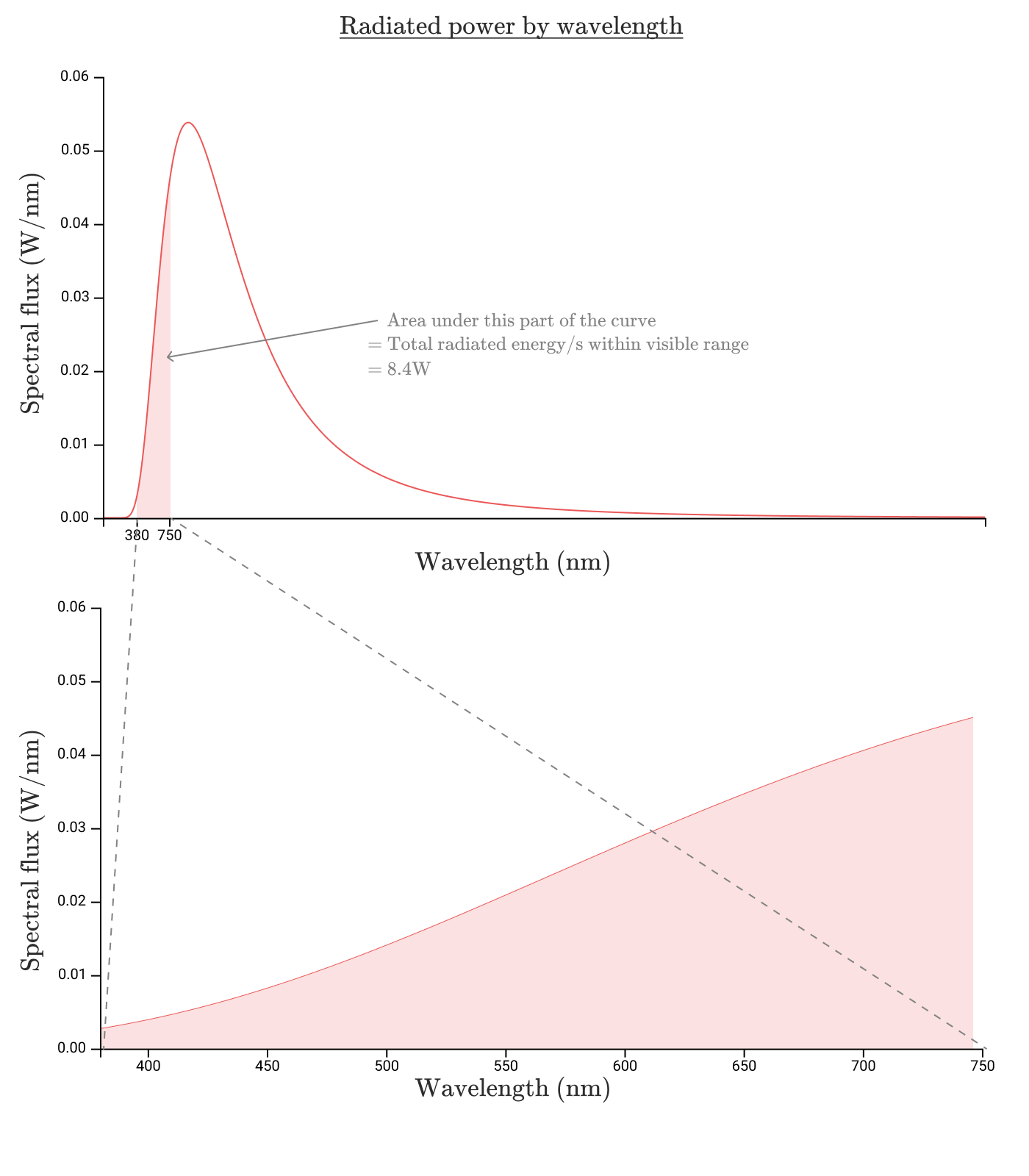
Итак, в видимом диапазоне излучается 8,7 Вт, что даёт нам КПД в 8,7%. Выглядит ужасно. На самом деле ситуация ещё хуже.

Чтобы понять почему, давайте рассмотрим, почему видимый свет является видимым.

Воспринимаемая на глаз яркость

Фото: Christopher Burns

Так же как лампа накаливания не одинаково излучает на всех длинах волн, наши глаза тоже не одинаково чувствительны к излучению во всех диапазонах. Если измерить чувствительность человеческого глаза к каждой длине волны, то мы получим функцию относительной спектральной световой эффективности монохроматического излучения. Стандартная функция спектральной световой эффективности $\bar y(\lambda)$ выглядит так:

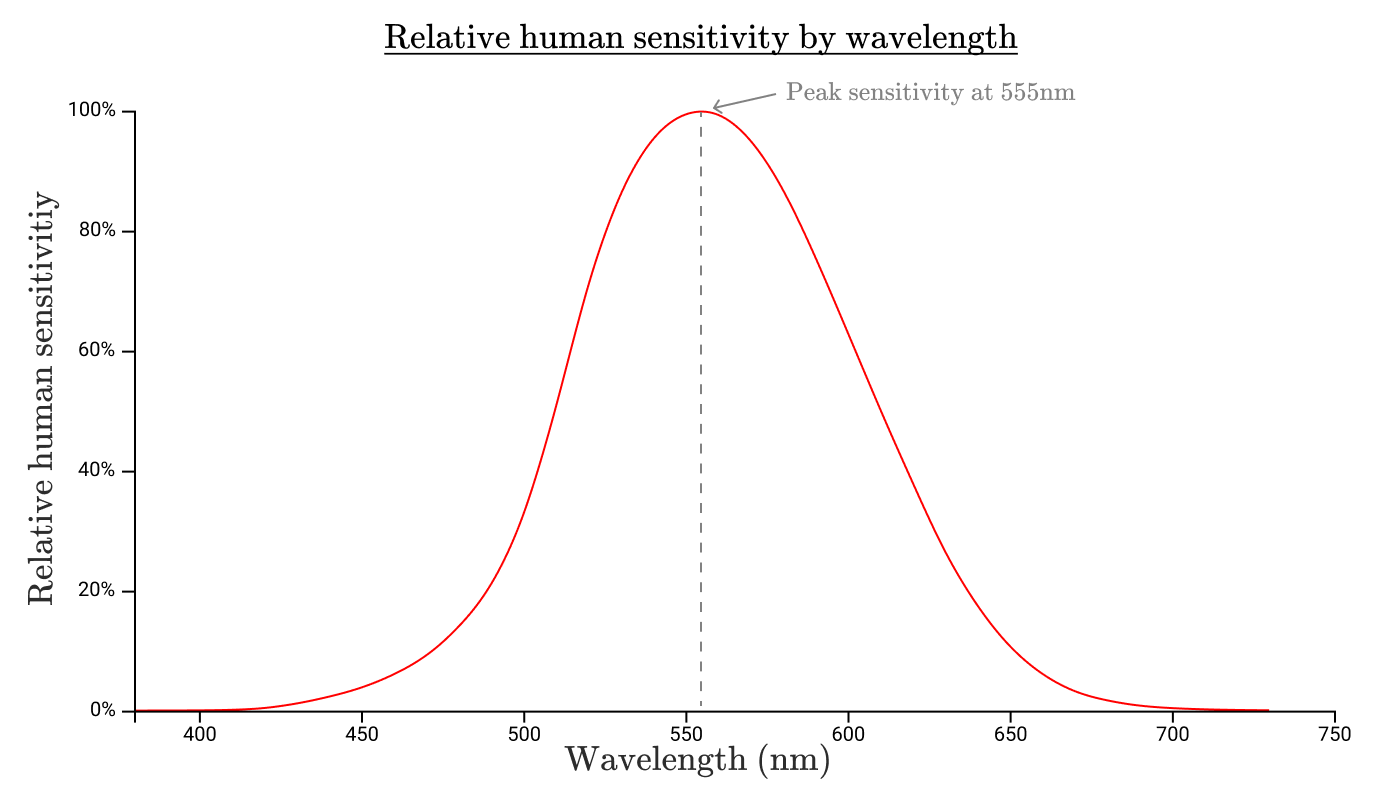
Границы этой функции определяют диапазон видимого света. Мы не увидим ничего за пределами этого диапазона, потому что наши глаза не воспринимают этот свет!

Данная кривая также показывает что наши глаза намного более чувствительны к излучению на 550 нм, чем к излучению на 650 нм или 450 нм.

Глаза других животных чувствительны к другим диапазонам волн и, следовательно, для них действуют другие функции относительной спектральной световой эффективности. Птицы могут видеть в ультрафиолете излучение в диапазоне от $\lambda=300\text{nm}$ до $\lambda=400\text{nm}$ , поэтому если бы учёные птицы писали научные статьи об электромагнитном спектре, именно эту часть диапазона они бы назвали «видимым светом»!

Фото: Timothy Rhyne

Умножив график спектральной плотности излучения на функцию относительной спектральной световой эффективности монохроматического излучения $\bar y(\lambda)$ , мы получим функцию, которая описывает вклад каждой длины волны, излучаемой источником света, в воспринимаемую человеком яркость.

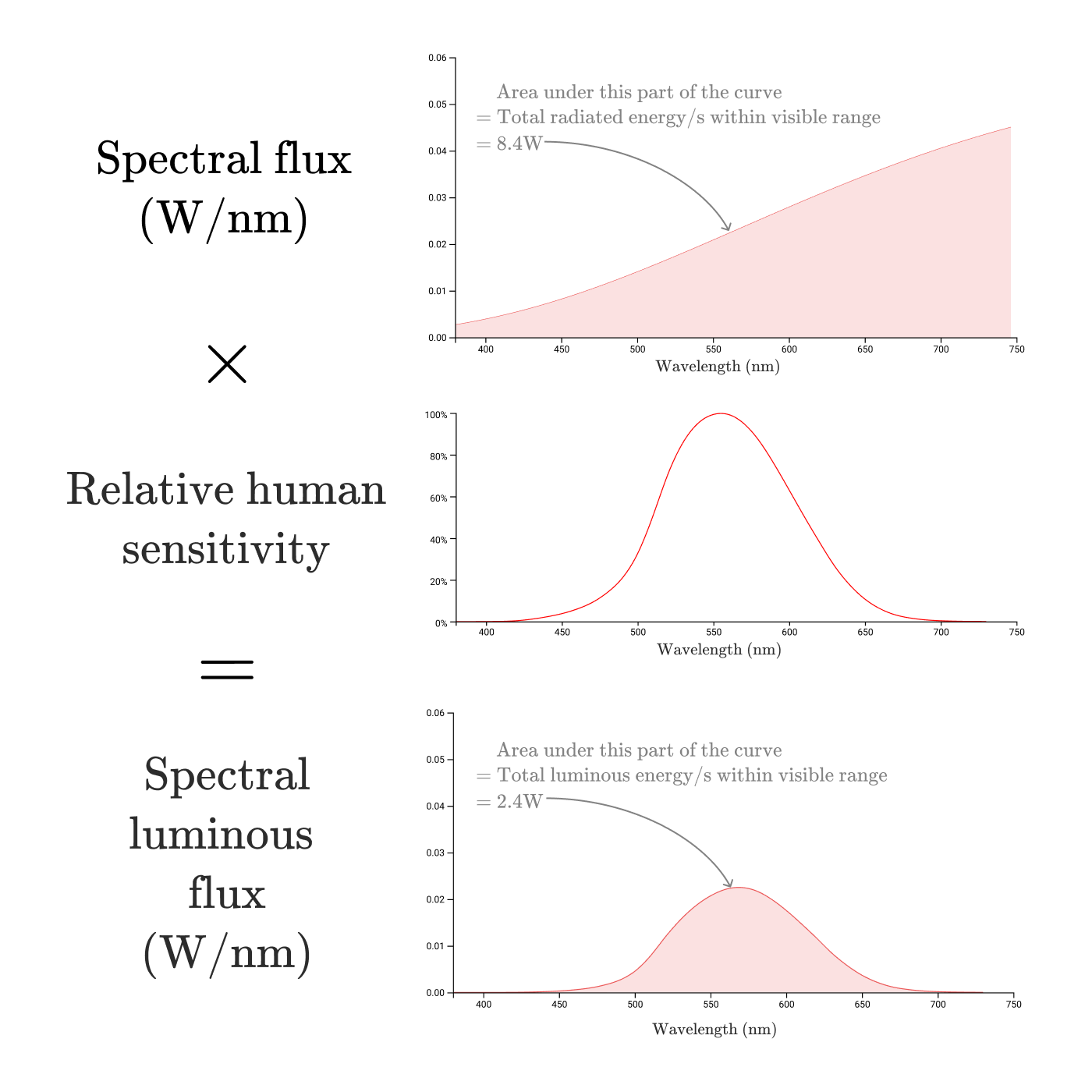
Это спектральная плотность светового потока ( $\Phi_{v,\lambda}$ ). Чтобы подчеркнуть связь с человеческим восприятием, а не объективной мощностью, световой поток измеряется в люменах, а не ваттах, с коэффициентом преобразования 683,002 лм/вт.

$\Phi_{v,\lambda}(\lambda) = 683.002 \frac{\text{lm}}{\text{W}} \cdot \bar y(\lambda) \cdot \Phi_{e,\lambda}(\lambda)$

Световой поток ( $\Phi_v$ ) от источника света — это общая воспринимаемая человеком сила света.

Точно так же, как мы рассчитывали поток излучения, посчитав площадь области, ограниченной кривой потока излучения, мы можем найти и световой поток, взяв область, ограниченную кривой спектральной плотности светового потока, с преобразованием из ватт воспринимаемого излучения в люмены:

$\Phi_{v}^\text{bulb} = \int_0^\infty \bar y(\lambda) \cdot \Phi_{e,\lambda}^\text{bulb}(\lambda) d\lambda = 683.002 \frac{\text{lm}}{\text{W}} \cdot 2.4\text{W} \approx 1600 \text{lm}$

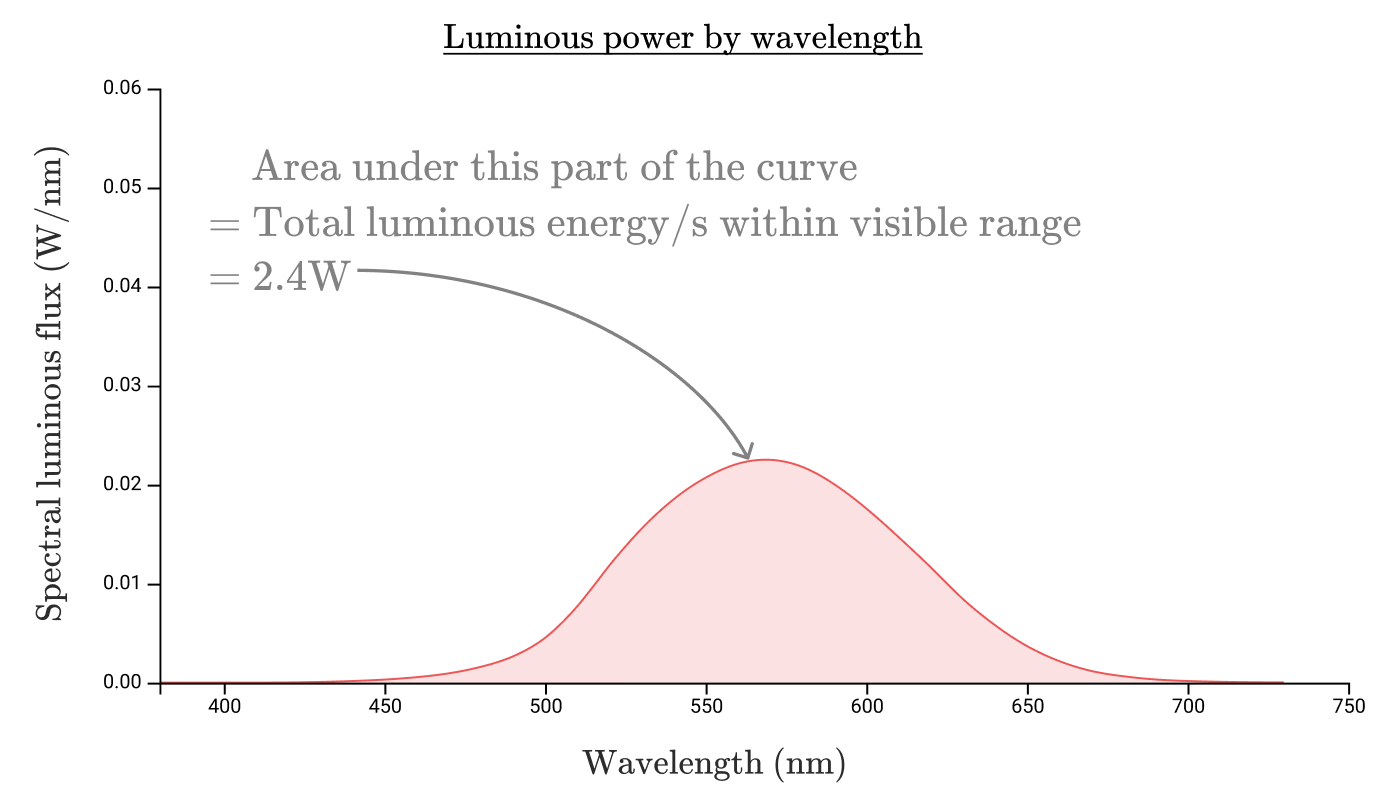
Так что световой поток нашей стоваттной лампы накаливания составляет жалкие 2,4 Вт или 1600 люмен! У лампы накаливания световая эффективность всего 2,4%, что далеко от эффективности 80% преобразования электроэнергии в излучение.

Возможно, если бы наш световой источник концентрировал своё излучение в видимом диапазоне, то можно было бы получить более эффективное освещение. Сравним спектры ламп накаливания, люминесцентных и светодиодных ламп:

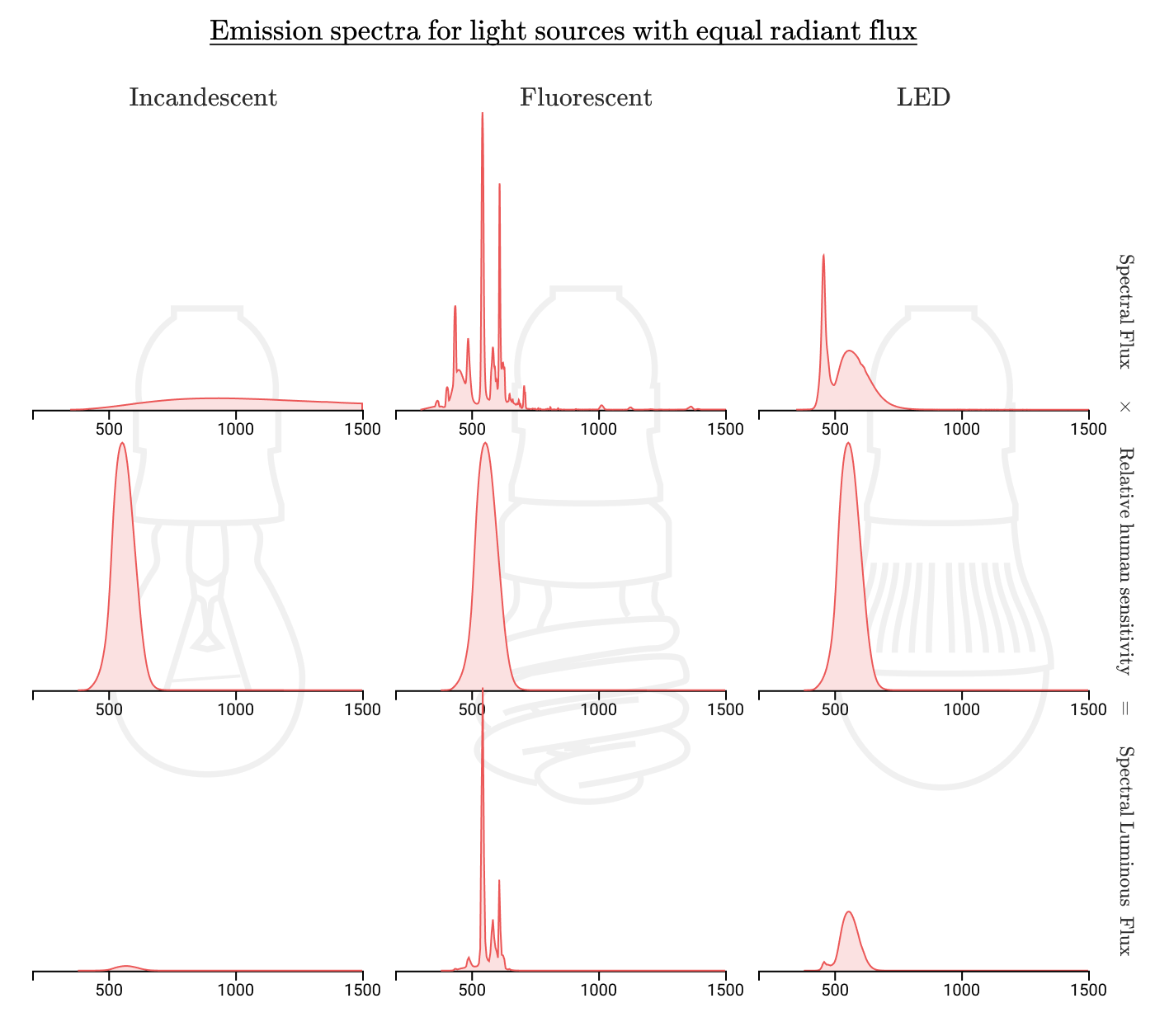
И действительно, люминесцентные и светодиодные лампы тратят гораздо меньше энергии в невидимых человеку диапазонах. Если у ламп накаливания эффективность 1–3%, то у люминесцентных ламп она около 10%, а у светодиодных — до 20%!

Но хватит о яркости, вернёмся к теме статьи: цвет!

Количественное определение цвета

Фото: Lauren Mancke

Как идентифицировать данный цвет? Если передо мной лимон, как сказать по телефону, какого он цвета? Я могу сказать, что «лимон жёлтый», но какой именно жёлтый? Как точно идентифицировать каждый из этих оттенков жёлтого?

Вооружившись знанием о том, что цвет — это интерпретация человеком электромагнитного излучения, может возникнуть соблазн определить цвет математически с помощью спектральной плотности излучения. Любой видимый человеком цвет будет неким взвешенным сочетанием монохроматических цветов (одиночных длин волн). Монохроматические цвета также известны как спектральные цвета.

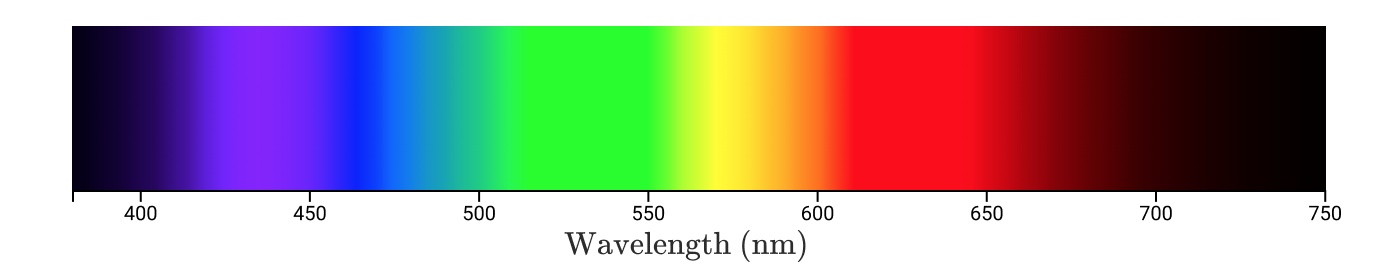
Монохроматические цвета по длинам волн

Для любого данного объекта можно измерить спектр излучения (или отражения) — и использовать его для точного определения цвета. Если можно воспроизвести спектр, то мы точно воспроизведём цвет!

У отражённого от точки на лимоне солнечного света может быть примерно такой спектр отражения:

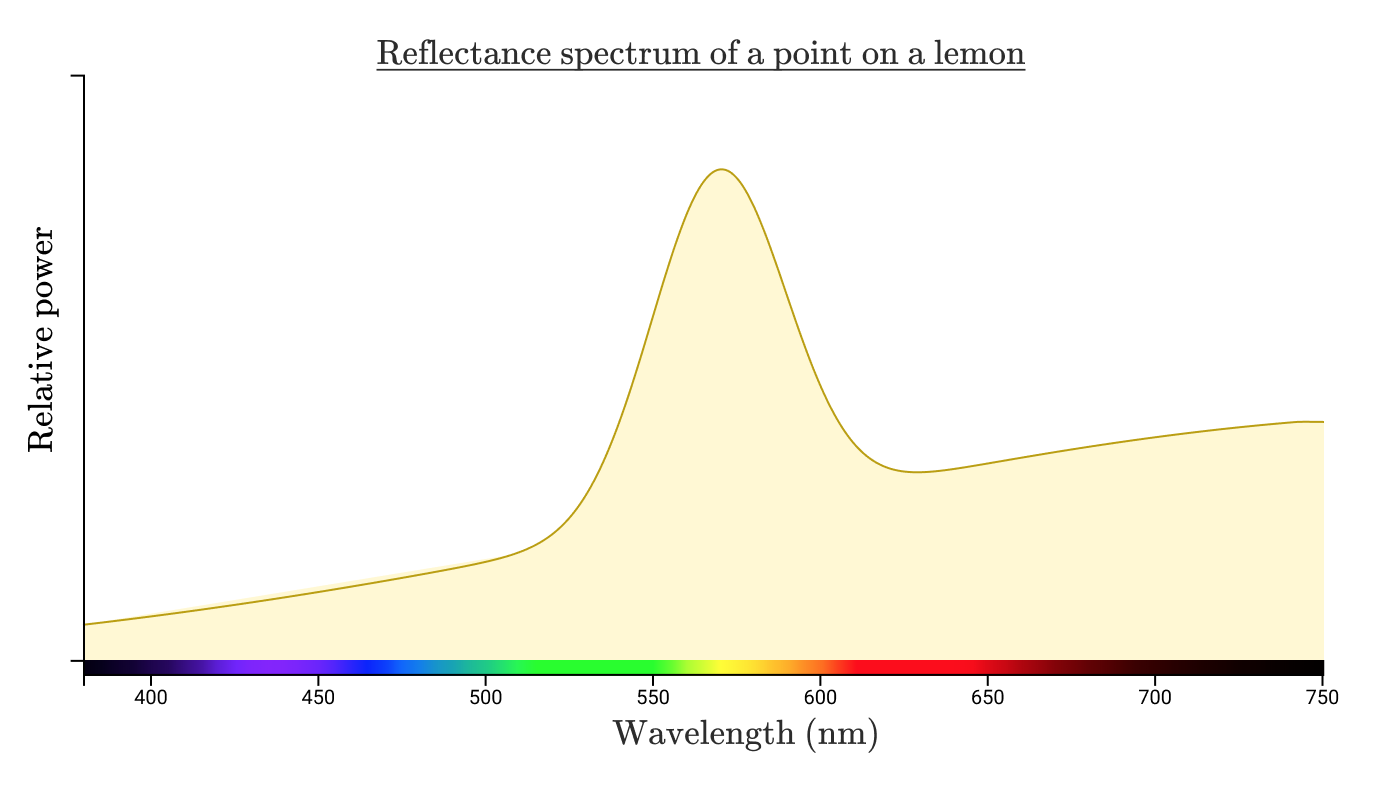
Примечание: мощность и распределение интенсивности излучения, достигающего глаза, зависит от мощности и спектра излучения источника света, расстояния от источника света до освещаемого объекта, размера и формы объекта, спектра поглощения объекта и расстояния от вас до объекта. Здесь много о чём нужно подумать, так что сосредоточимся на том, что происходит, когда этот свет достигает глаза человека. Пока проигнорируем единицы измерения и сосредоточимся на концепциях.

Когда энергия с таким спектральным распределением попадает в глаз человека, он воспринимает её как «жёлтую». Предположим, я сфотографировал лимон и загрузил фотографию на компьютер. Потом тщательно настроил цвета на экране, чтобы конкретная точка лимона на экране не отличалась от цвета фактического лимона в моей реальной руке.

Если вы измерите распределение спектральной интенсивности с экрана, то как по-вашему оно будет выглядеть? Разумно ожидать, что оно похоже на спектр отражения лимона выше. Но на самом деле оно выглядит примерно так:

Два разных распределения спектральной интенсивности, выглядящие одинаково для наблюдателя-человека, называются метамерами.

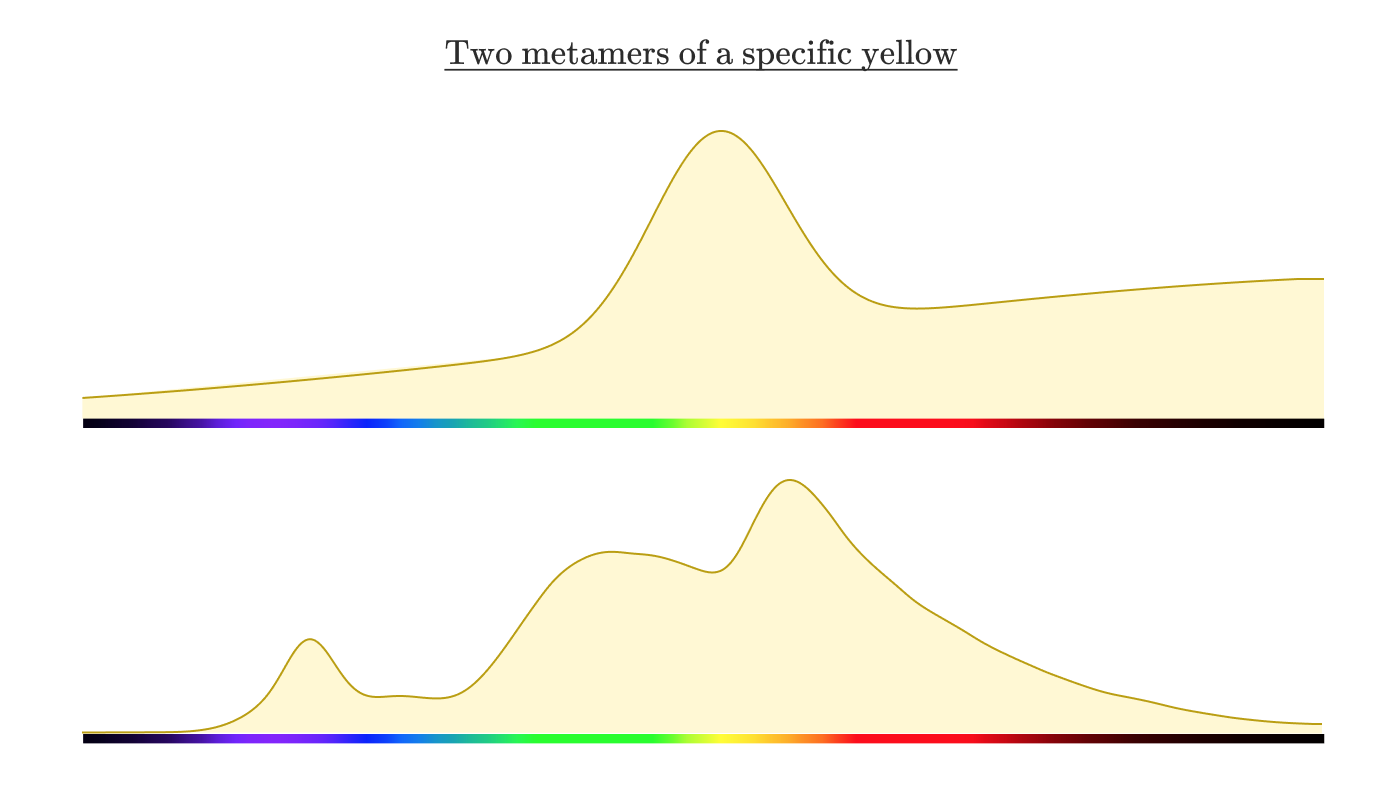
Чтобы понять, как такое возможно, рассмотрим биологию глаза.

Оптическая биология

Фото: Аманды Далбьерн

За наше восприятие света отвечают специализированные клетки в сетчатке глаза, палочки и колбочки. Палочки важны преимущественно в условиях низкой освещенности и не играют большой роли в восприятии цвета, поэтому мы сосредоточимся на колбочках.

У людей как правило три вида колбочек. Наличие трёх разных видов колбочек делает человека «трихроматом». Однако есть по крайней мере один подтверждённый случай человека-тетрахромата! У другие животных даже больше видов колбочек. У ротоногих — шестнадцать видов.

Каждый тип колбочки обозначен по длинам световых волн, на которые он реагирует. Стандартное обозначение — S, M и L (короткие, средние, длинные волны).

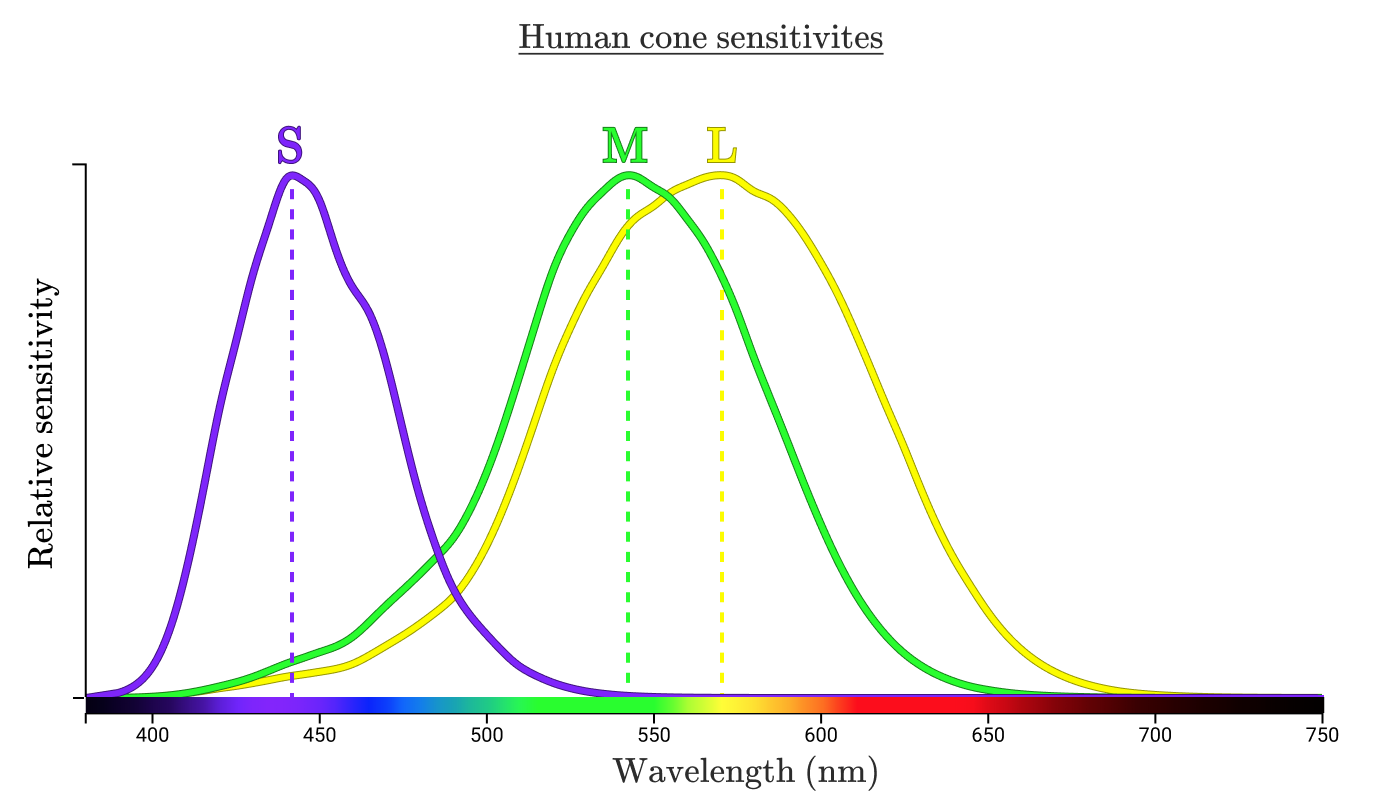
Три кривые показывают, насколько чувствительны колбочки определённого типа к каждой длине волны. Наивысшая точка каждой кривой называется «пиковой длиной волны», указывая длину волны, к которой колбочка наиболее чувствительна.

Посмотрим, как наши колбочки обработают свет, отражающийся от лимона в руке.

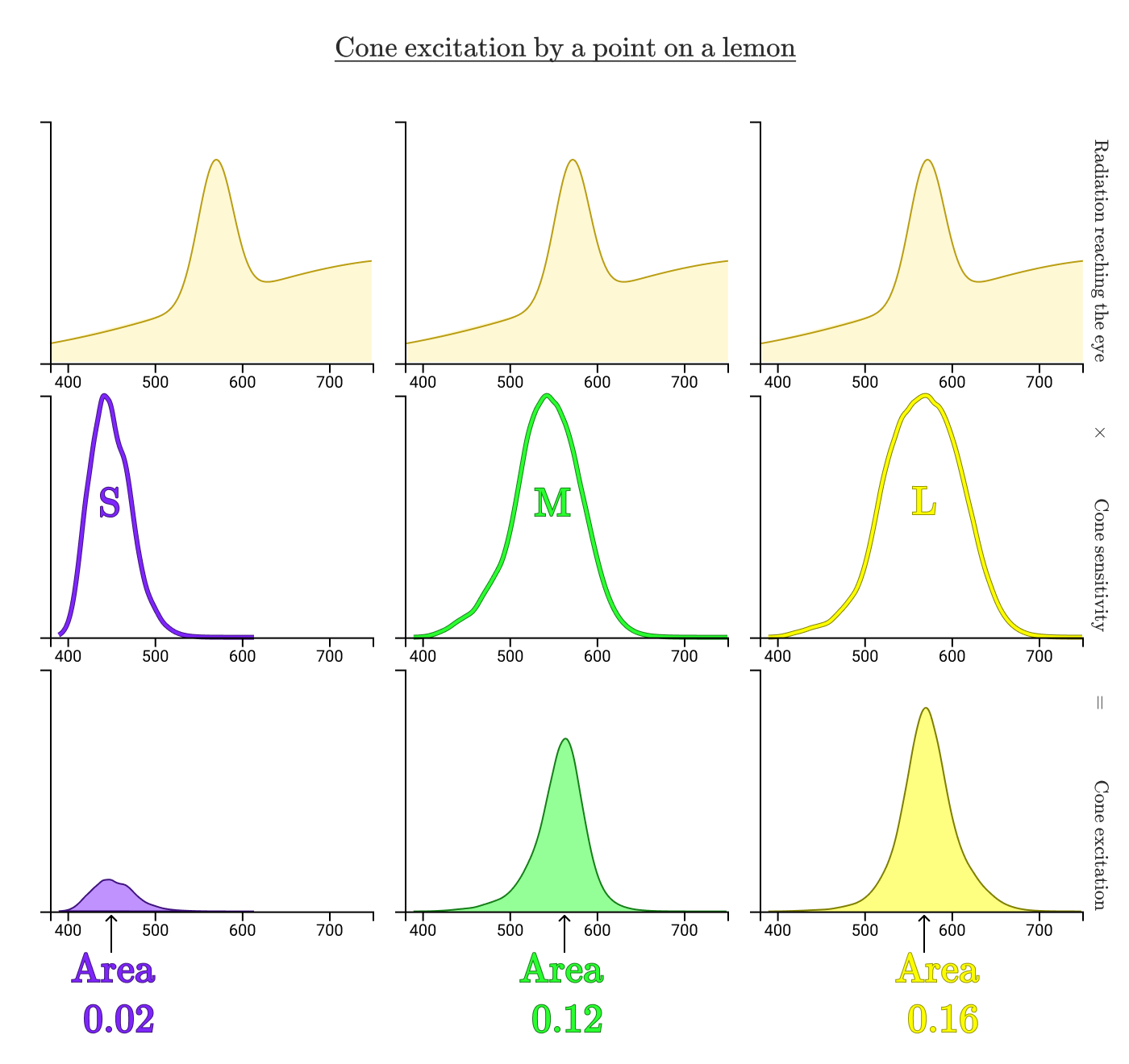
Ограниченные кривыми области показывают, какая часть отражённого от лимона излучения возбуждает каждый тип колбочек. В данном случае нормализованные возбуждения колбочек S, M и L составляют 0,02, 0,12 и 0,16, соответственно. Теперь повторим процесс для лимона на экране.

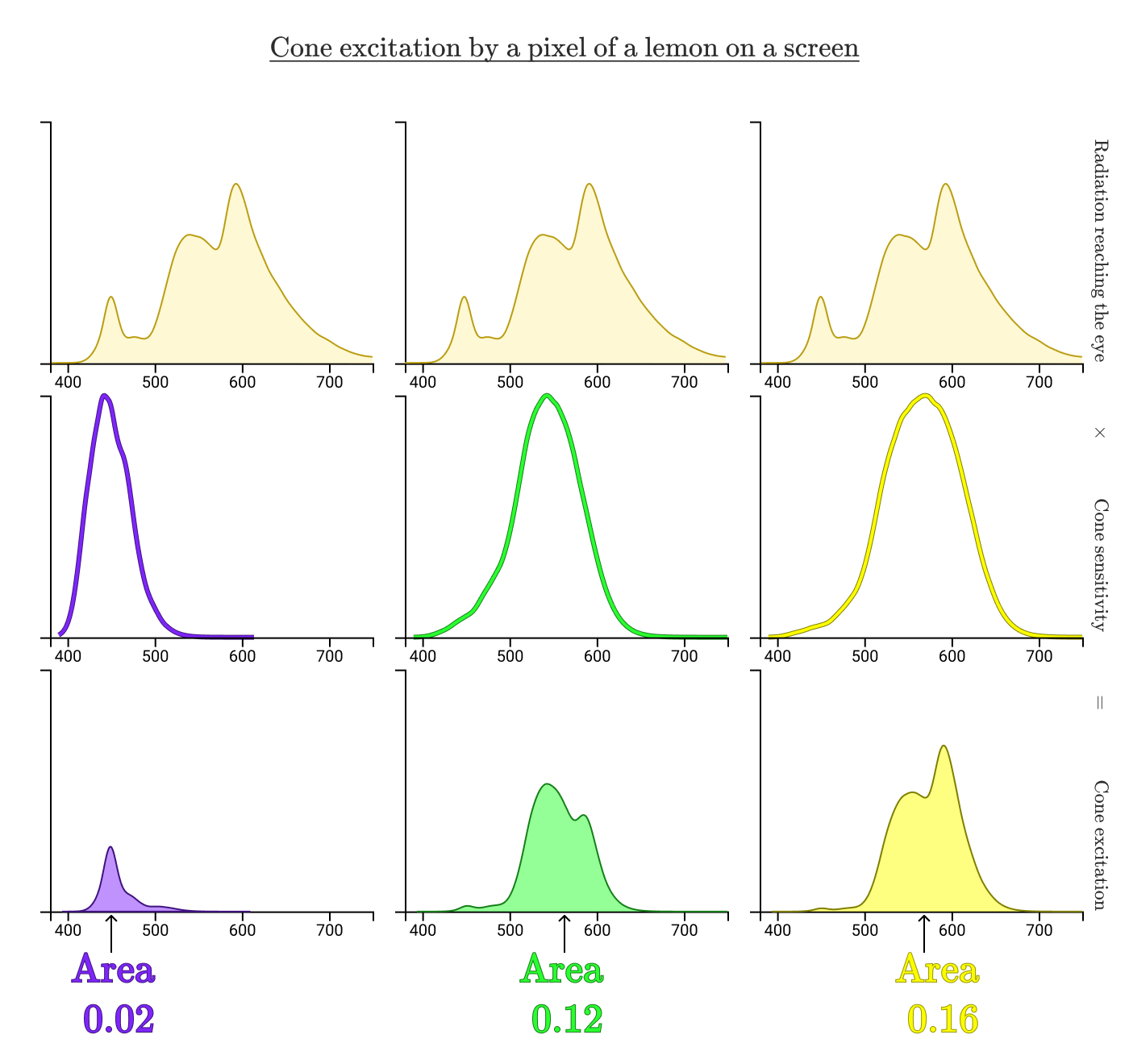
Несмотря на совершенно разные спектры излучения, возбуждения колбочек одинаковы (S=0,02, M=0,12, L=0,16). Вот почему точка на реальном лимоне и точка на цифровом лимоне для нас выглядят одинаково!

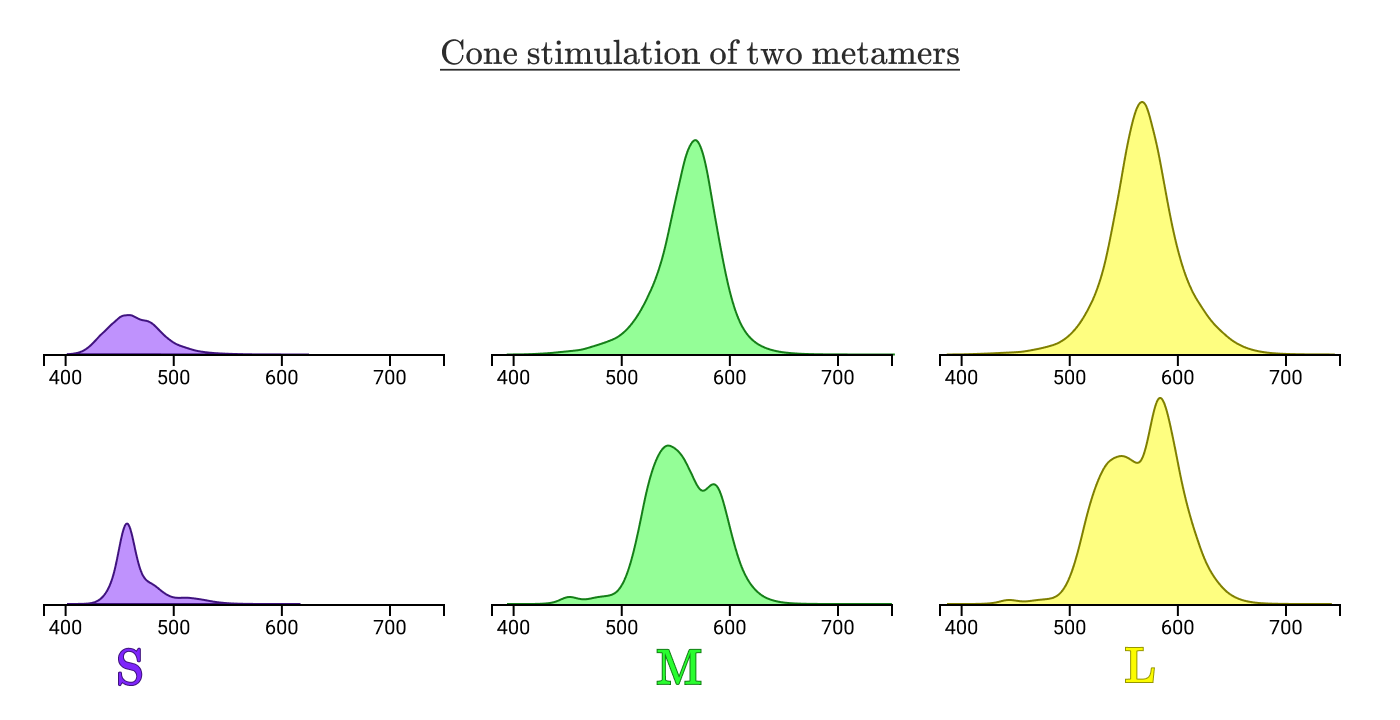
У метамер всегда будет равна нормализованная площадь под кривыми стимуляции трёх типов колбочек

Наши три набора колбочек сводят любую кривую спектральной плотности потока $\Phi_e(\lambda)$ к триплету чисел $(S, M, L)$ , а каждый отдельный триплет будет отдельным цветом! Это довольно удобно, потому что с отдельными цифрами (0,02, 0,12, 0,16) гораздо проще работать, чем со сложной непрерывной функцией. Для любителей математики: наши глаза производят размерную редукцию из бесконечномерного пространства в три измерения — чертовски круто уметь бессознательно вытворять такое.

В реальности триплет $(S, M, L)$ — это наш первый пример цветового пространства.

Цветовые пространства
Цветовые пространства позволяют численно определить цвет. В предыдущей главе мы видели, что определённый жёлтый цвет можно представить как (0,02, 0,12, 0,16) в цветовом пространстве SML, которое более известно как цветовое пространство LMS.

Поскольку это цветовое пространство описывает стимуляцию конусов, по определению любой видимый цвет человека можно представить положительными координатами LMS (за исключением крайне редких людей-тетрахроматов, которым нужны четыре координаты вместо трёх).

К сожалению, у этого цветового пространства есть некоторые бесполезные свойства.

Во-первых, не все значения триплетов (также называемые цветовыми компонентами или координатами цвета) физически возможны. Например, координаты LMS (0, 1, 0). Чтобы выйти на эту координату, нужно как-то стимулировать колбочки М, при этом вообще не стимулируя колбочки L и S. Но это невозможно, потому что кривая чувствительности колбочек M значительно перекрывает L или S на всех длинах волн!

Любая длина волны, которая стимулирует колбочки M, также будет стимулировать колбочки типа L или S (или оба типа!)

В итоге возникает проблема, что реально сложно увеличить стимуляцию только одного типа колбочек. Из-за такого побочного эффекта, в частности, данная цветовая модель не очень совместима с производством дисплеев.

Другая историческая, практическая проблема заключается в том, что точной чувствительности колбочек не знали до 1990-х годов, а необходимость разработки математически точной модели цвета возникла намного раньше. Первый значительный прогресс в этой области произошёл в конце 1920-х.

Эксперименты Райта и Гилда по сложению цветов
В конце 1920-х годов Уильям Дэвид Райт и Джон Гилд провели эксперименты. Они точно определили отдельные цвета по вкладу трёх конкретных длин волн.

Хотя они, вероятно, не знали о трёх типах колбочек на сетчатке, но ещё за сто лет до них возникла идея, что все видимые цвета можно представить как комбинацию трёх цветов.

Пример трёхцветной теории цвета Чарльза Хейтера, 1826 год

У Райта и Гилда появилась идея построить аппарат, который позволит испытуемым определять тестовый цвет как комбинацию от трёх источников света с фиксированной длиной волны. Установка выглядела примерно так:

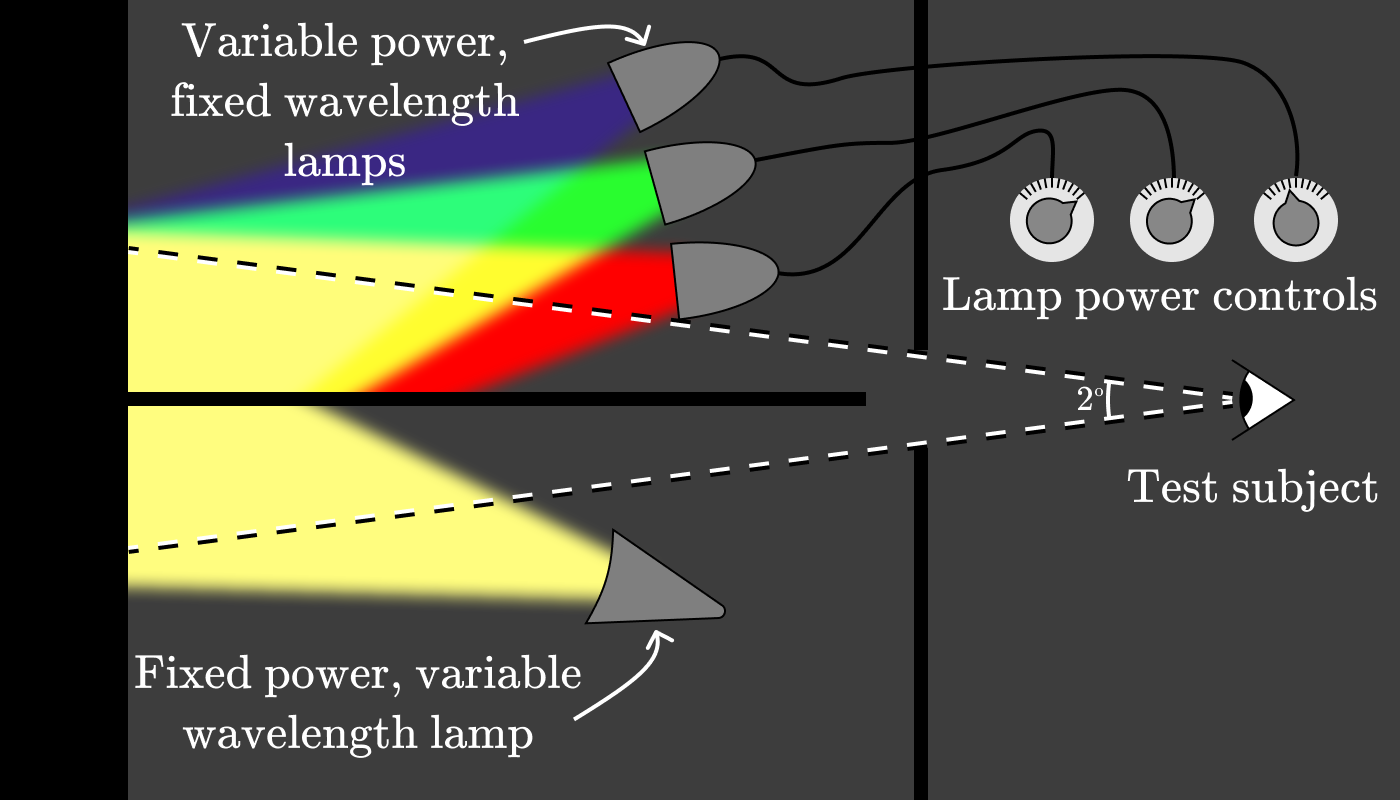
Экспериментатор настраивал лампу внизу на определённую длину волны, (например, 600 нм), а затем просил испытуемых отрегулировать питание трёх контрольных ламп, чтобы цвет совпадал.

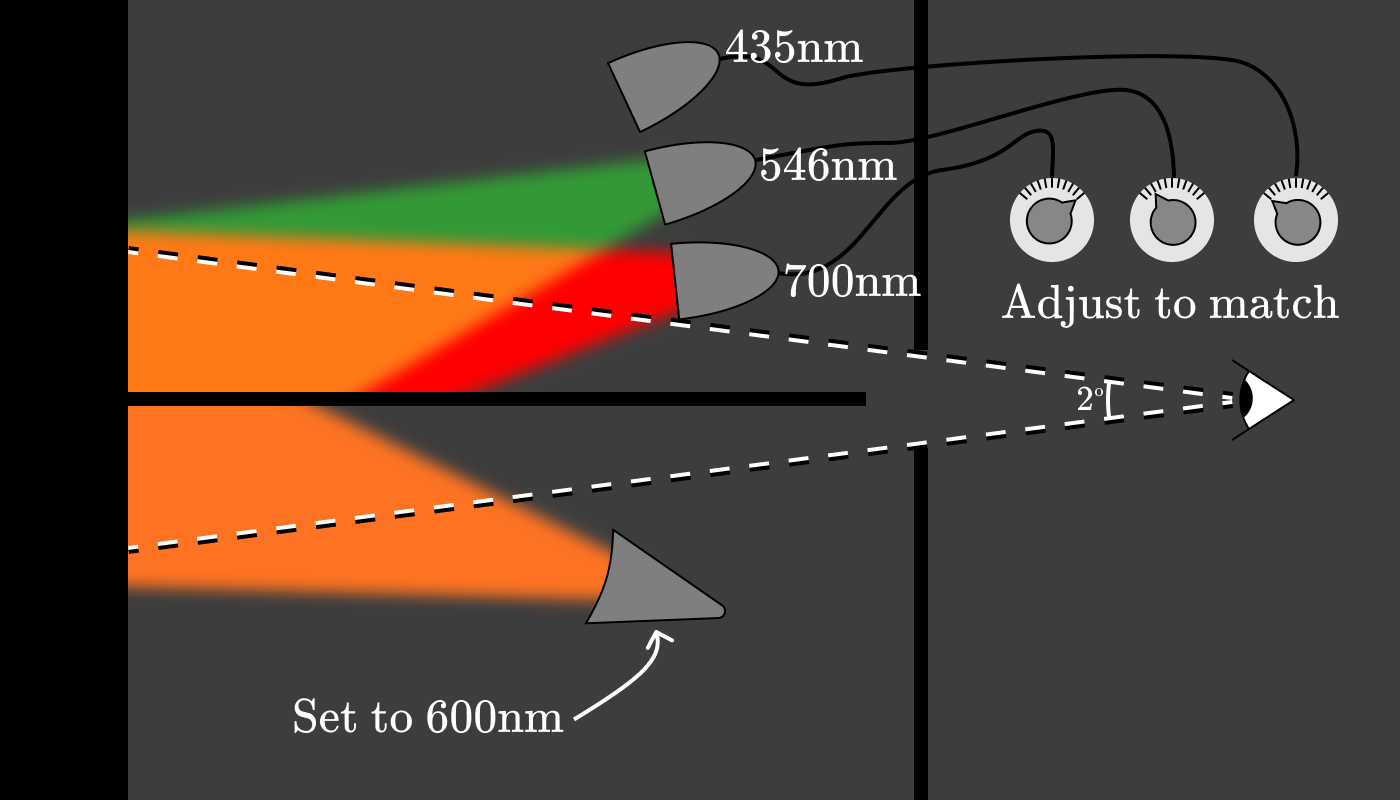
Мощность каждой из трёх ламп (красный, зелёная и синяя) дают нам триплет чистых спектральных цветов, который соответствует 600 нм. После повторения этого эксперимента через каждые 5 нм примерно на десяти испытуемых, был создан график, показывающий количество красного (700 нм), зеленого (546 нм) и синего (435 нм) света, необходимого для восстановления внешнего вида цвета на заданной длине волны. Функции известны как функции сложения цветов (color matching function, CMF).

Эти конкретные функции сложения цветов известны как $\bar r(\lambda)$ , $\bar g(\lambda)$ и $\bar b (\lambda)$ .

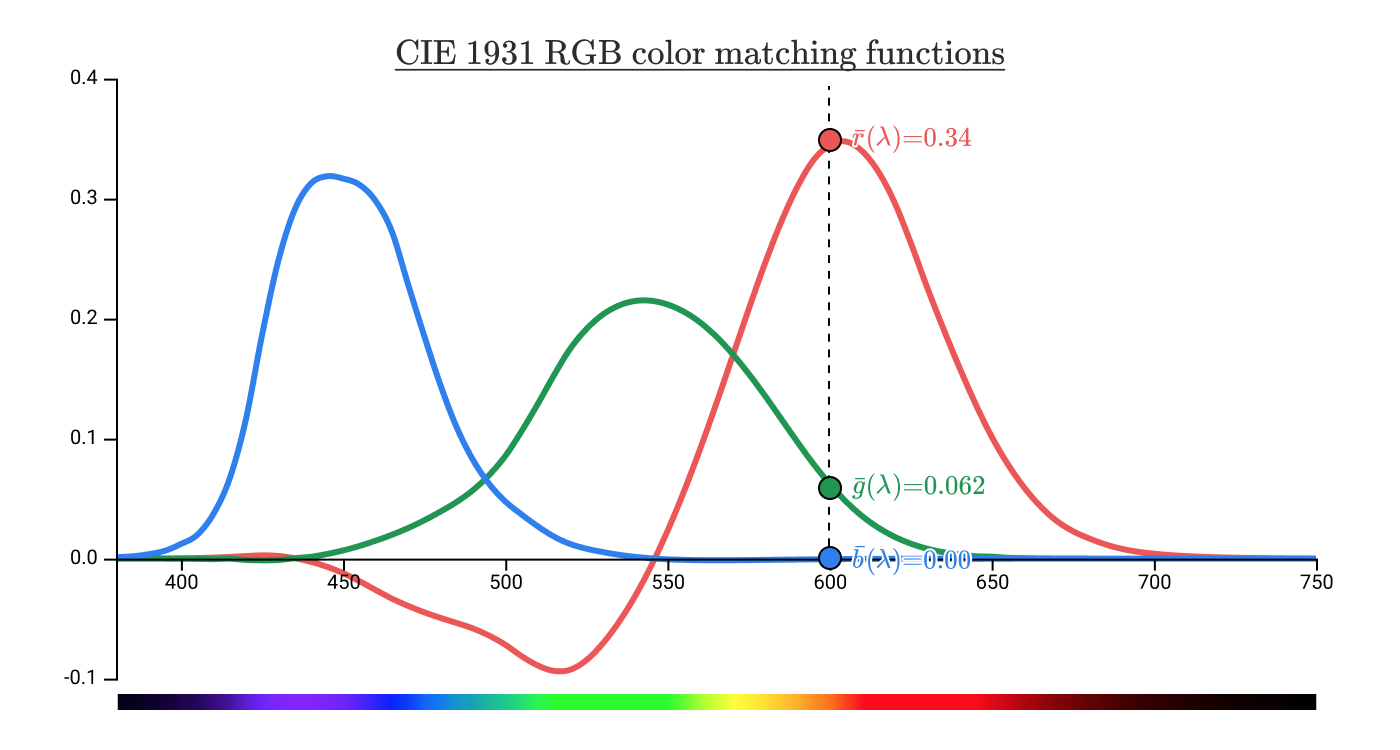
Они дают чистый спектральный цвет, который ассоциируется с длиной волны 600 нм по $(R, G, B)$ координатам (0,34, 0,062, 0.00). Это значение цвета в цветовом пространстве CIE 1931 RGB.

Подождите, а что означают негативные значения функции?

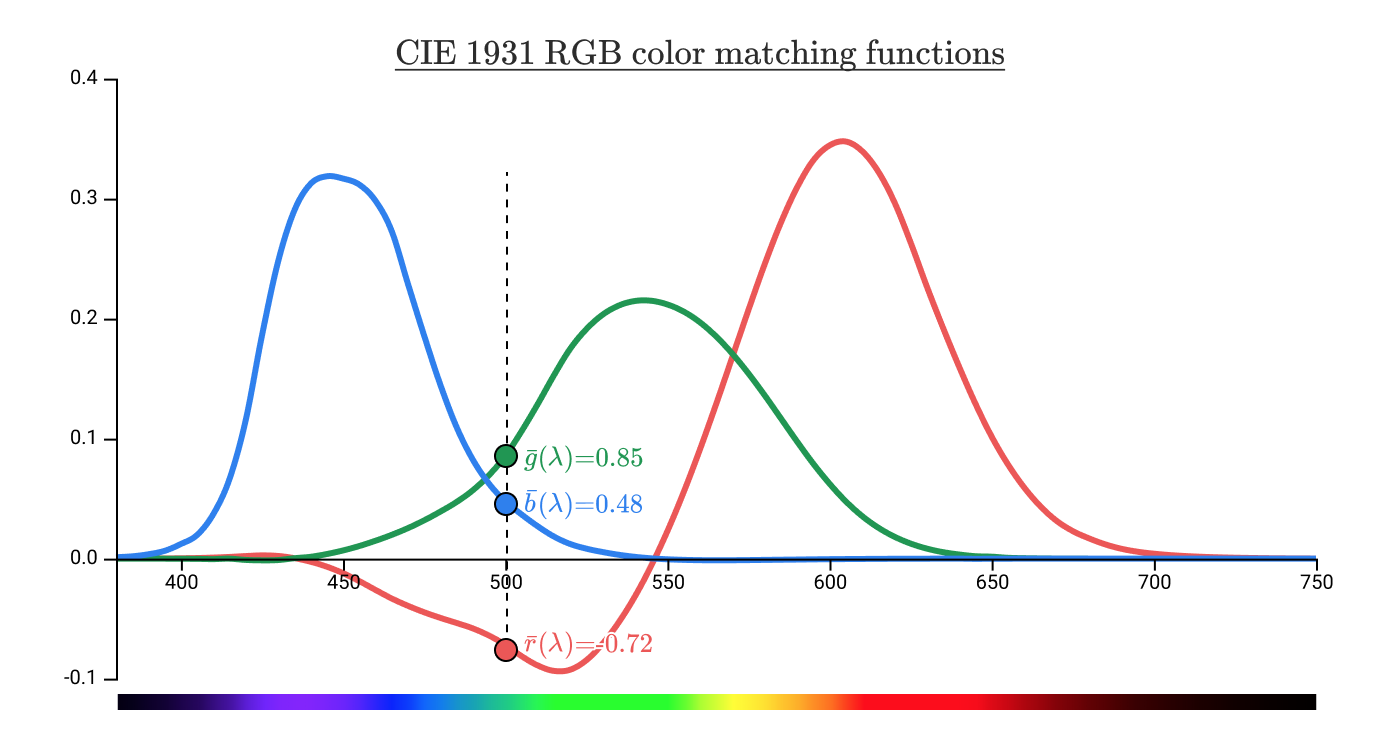
У чистых спектральных цветов, которые ассоциируются с цветом на длине волны 500 нм, координаты $(R, G, B)$ равны (−0,72, 0,85, 0,48). Так что именно означает это −0,72?

Оказывается, никакие параметры красной (700 нм) лампы вверху не позволяют достичь соответствия цвету 500 нм внизу, независимо от мощности синей и зелёной лампы вверху. Но можно достичь совпадения с двух сторон, если перенести красную лампу вниз.

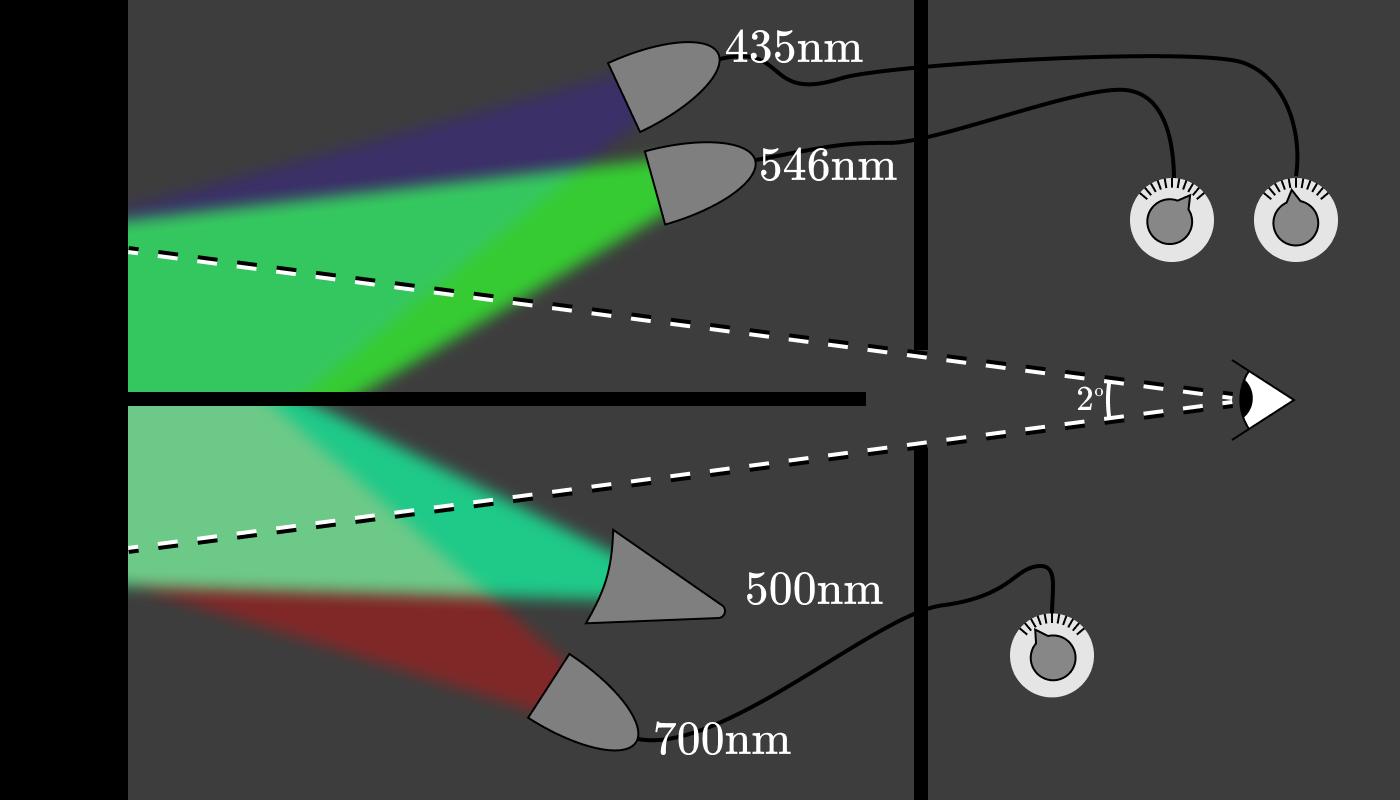
В реальной экспериментальной установке, наверное, сверху и снизу было установлено по полному набору ламп с фиксированными длинами волн, чтобы регулировать каждую из них в «отрицательной» зоне.

Используя наши функции сложения цветов, можно найти соответствие для любого монохроматического света с помощью сочетания (возможно, отрицательного) количества красного (700 нм), зелёного (546 нм) и синего (435 нм) света.

Функции сложения цветов можно проанализировать так же, как мы анализировали чувствительность колбочек L, M и S. Возьмём тот же цвет лимона:

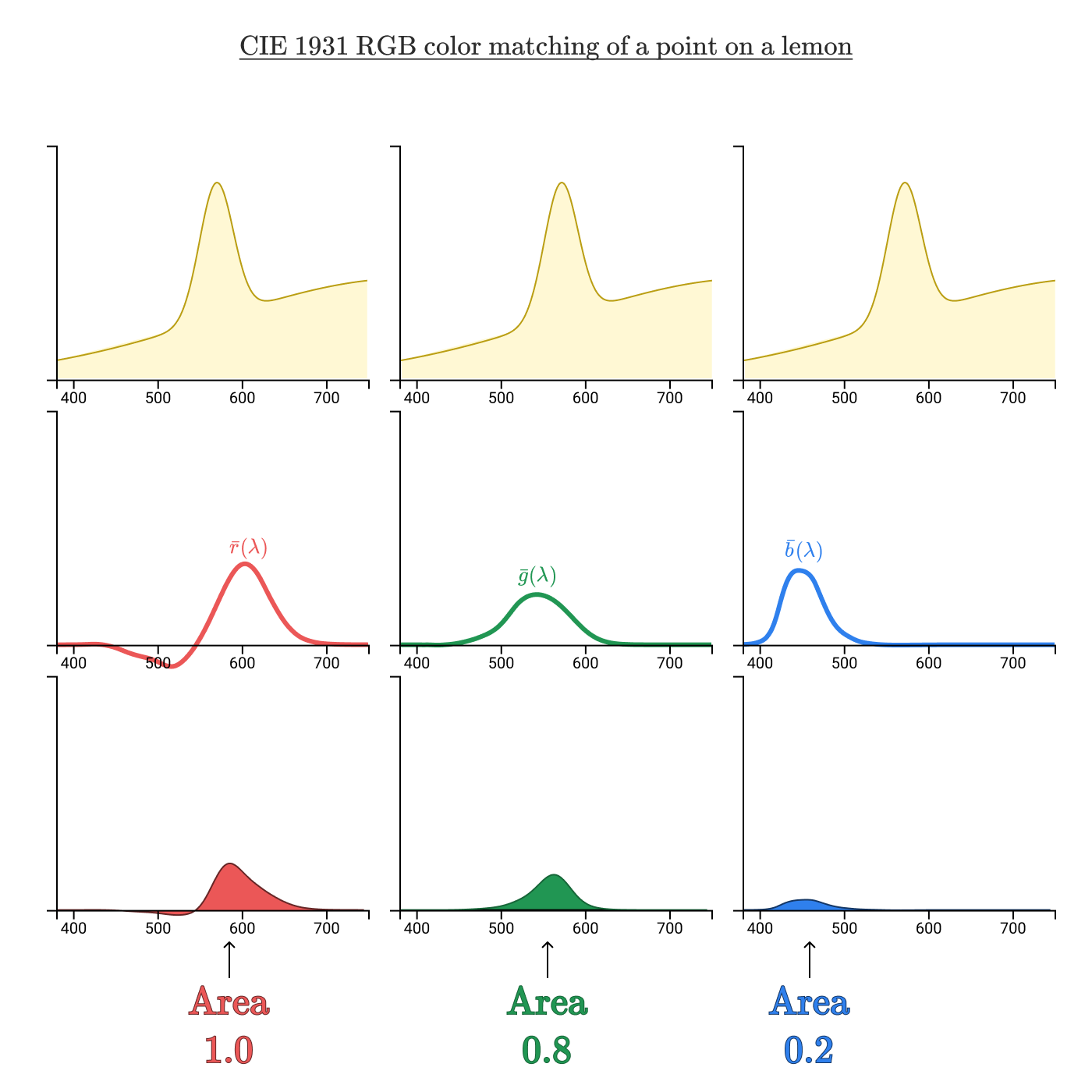
Взяв области, ограниченные кривыми произведения спектральной кривой и функций сложения цветов, мы получили RGB-триплет (1,0, 0,8, 0,2), однозначно идентифицирующий данный цвет.

В то время как цветовое пространство $(L, M, S)$ позволяет точно определить цвет, цветовое пространство $(R, G, B)$ даёт способ его точно воспроизвести, за исключением цветов с отрицательной координатой.

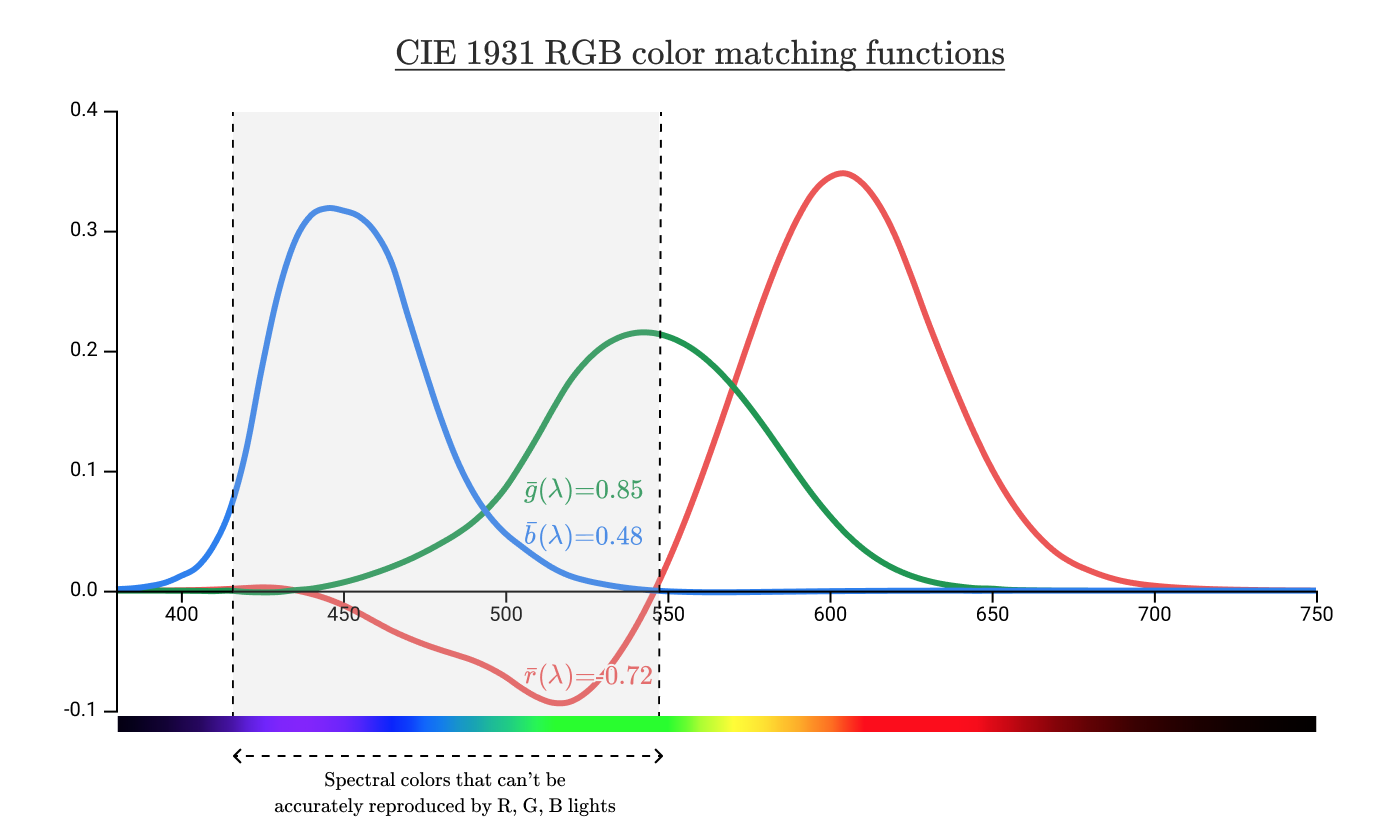
Но этот график показывает только какие спектральные цвета нельзя воспроизвести. А что насчёт неспектральных цветов? Можно ли произвести розовый цвет сочетанием R, G, B? Или циан (сине-зелёный цвет)?

Чтобы ответить на эти вопросы, нам понадобится лучший способ визуализации цветового пространства.

Визуализация цветовых пространств и хроматичности
До сих пор в большинстве диаграмм мы располагали длины волн по горизонтальной оси, размещая несколько графиков друг за другом в одной плоскости.

Вместо этого можно представить цвет как функцию $(R, G, B)$ или $(L, M, S)$ . Посмотрим, как выглядит цвет в трёхмерном пространстве .

Классно! Здесь отображается более широкий набор цветов, а не только спектральные цветов радуги.

Чтобы свести к двум измерениям, проще всего сделать отдельные диаграммы для каждой пары значений, например:

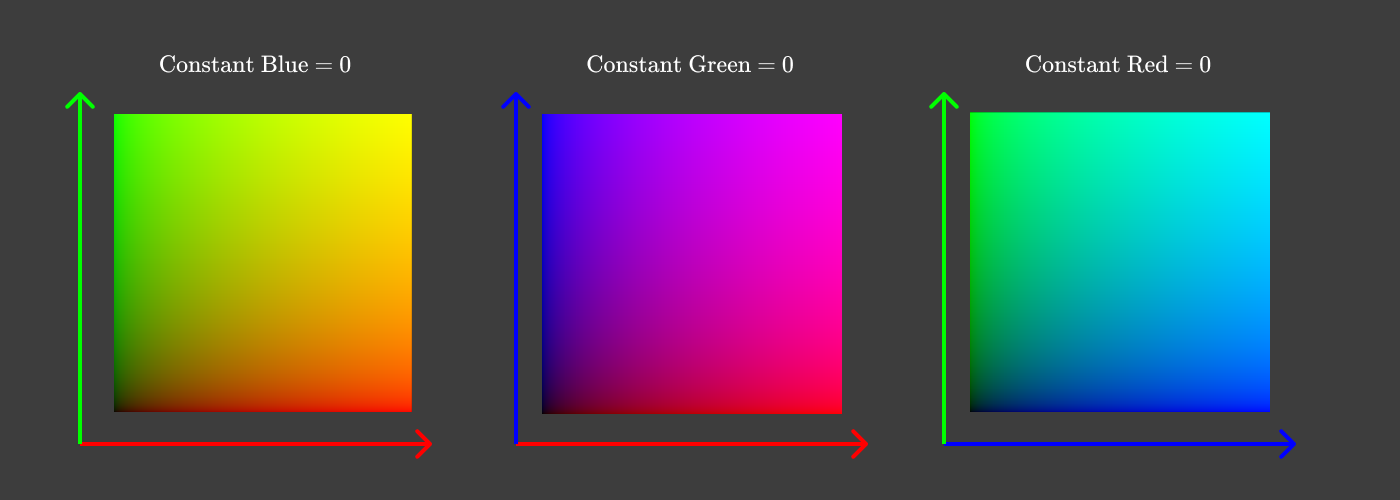
Пары компонентов с нулевой третьей составляющей

На каждой из диаграмм мы отбросили одно измерение, обнулив одну из трёх цветовых составляющих. Но вместо фиксации красной, зелёной или синей составляющих удобнее было бы увидеть все цвета, зафиксировав светлоту.

Вновь взглянув на куб мы видим, что (0, 0, 0) соответствует чёрному цвету, а (1, 1, 1) — белому.

Что произойдёт, если мы срежем куб по диагонали через плоскость, содержащую $(1, 0, 0)$ , $(0, 1, 0)$ и $(0, 0, 1)$ ?

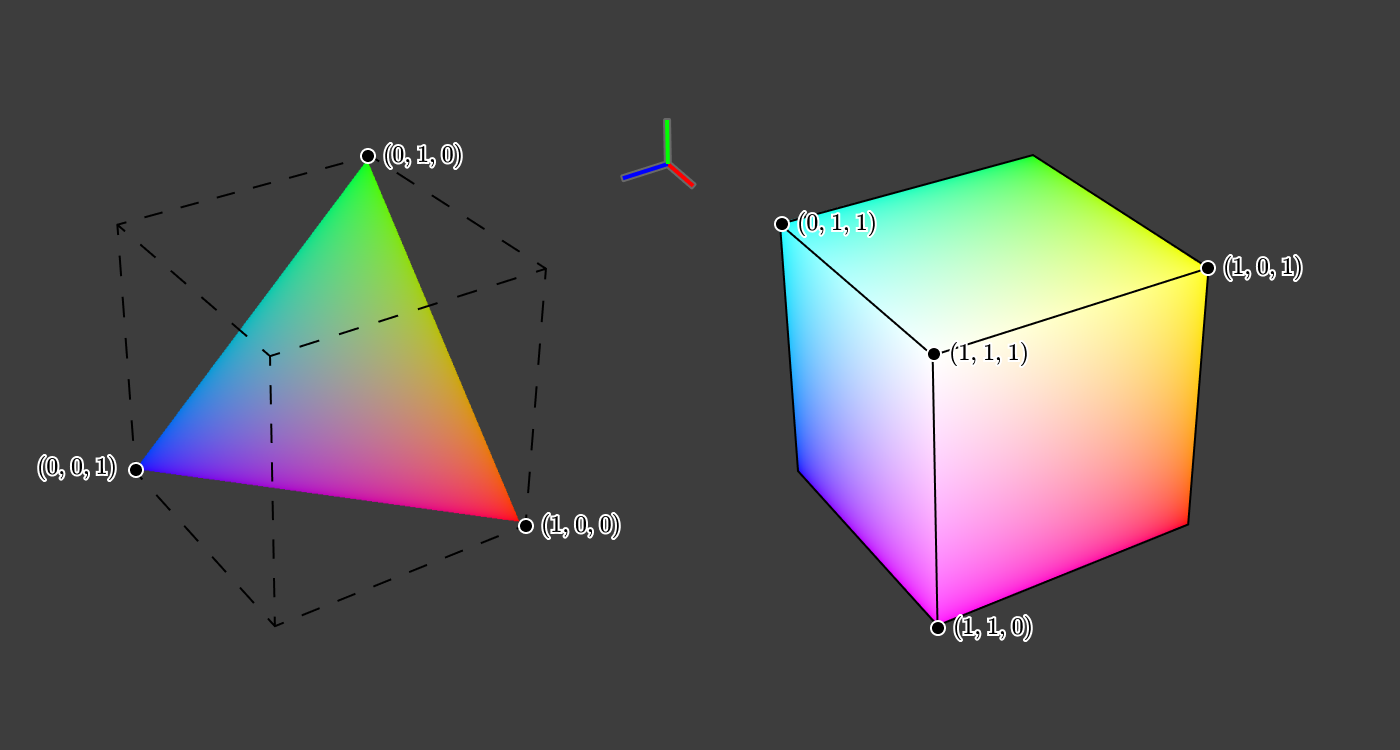
Этот треугольный срез куба обладает таким свойством, что $R + G + B = 1$ , и мы можем использовать $R + G + B$ как грубое приближение светлоты. Если посмотреть на треугольный срез сверху, то получим такое:

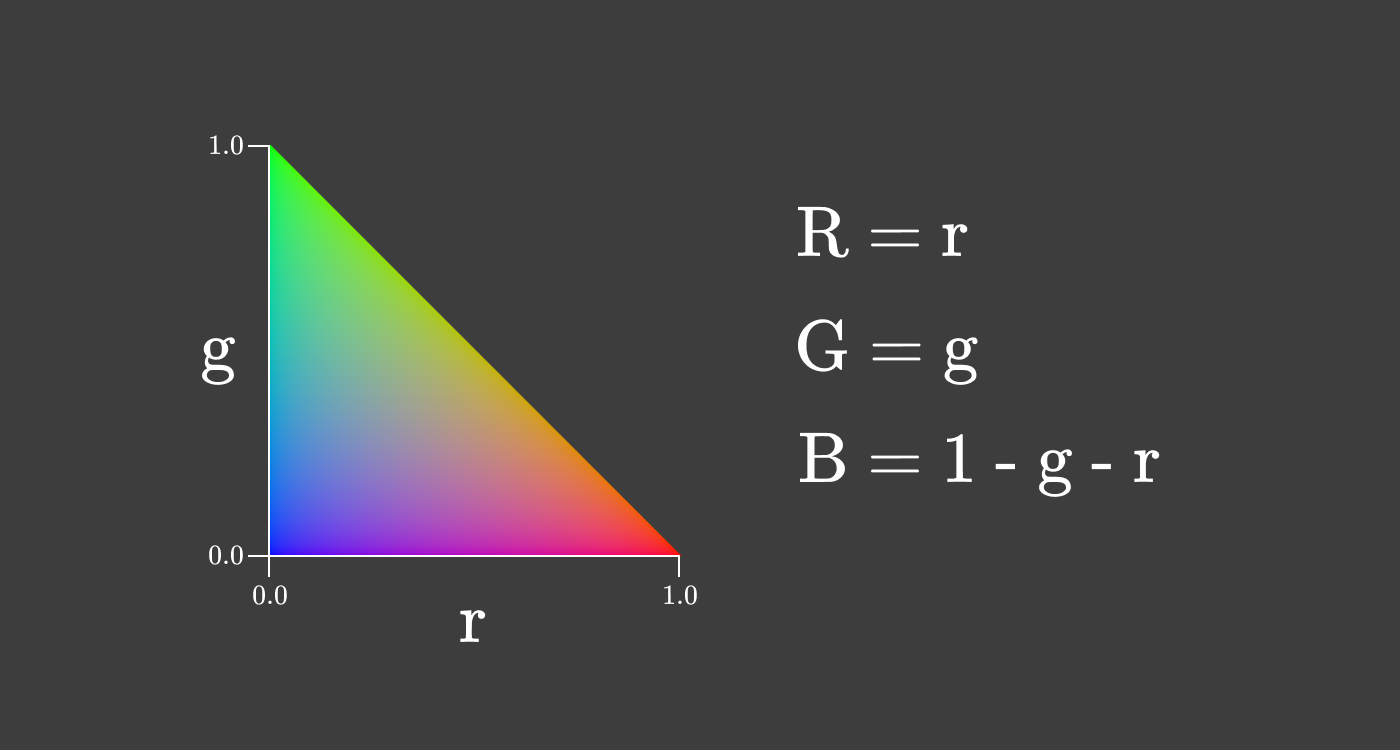
Такое двумерное представление цвета называется хроматичностью (chromaticity). Этот конкретный вид называется rg-хроматичностью. Хроматичность даёт информацию о соотношении основных цветов независимо от светлоты.

Это значит, что одинаковую хроматичность можно сохранять на разных уровнях светлоты.

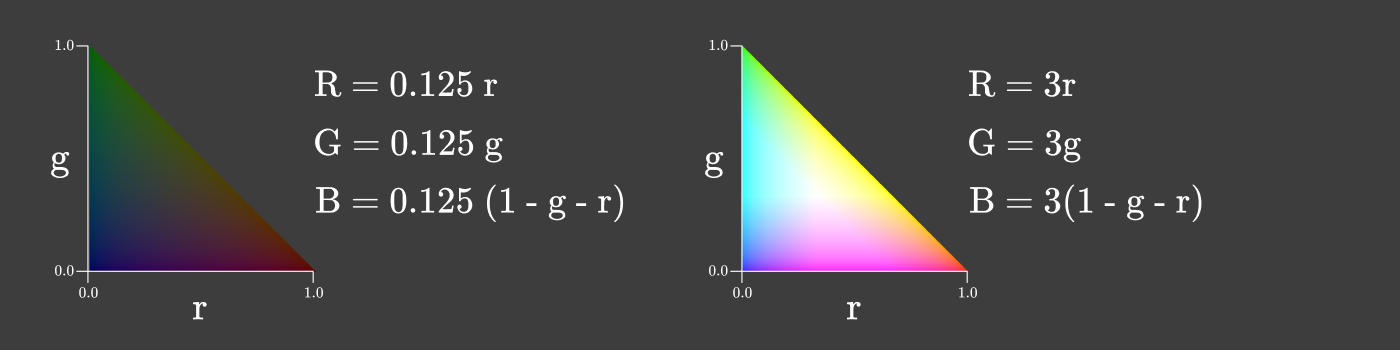
Можно даже сделать диаграмму хроматичности, где интенсивность изменяется вместе с r и g, чтобы максимизировать интенсивность при сохранении соотношения между R, G и B.

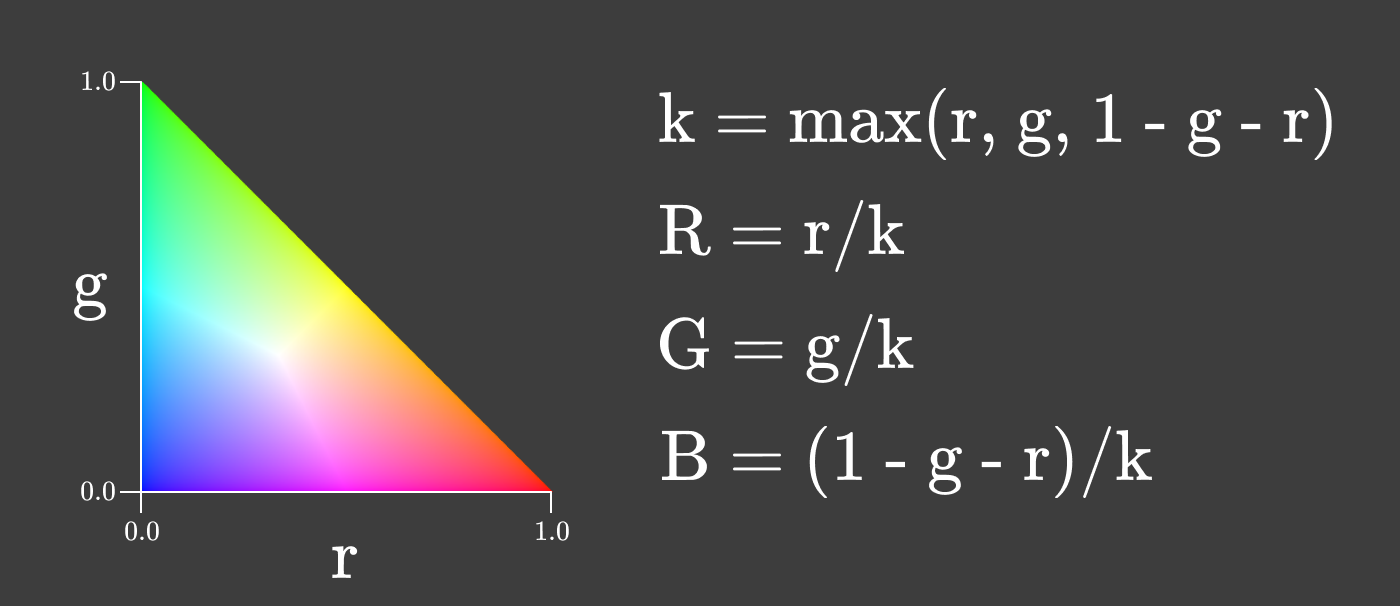
Хроматичность — полезное свойство цвета, потому что она не меняется при изменении интенсивности источника света, пока у источника тот же спектральный состав. При изменении яркости экрана хроматичность остаётся постоянной!

Существует много способов разделить хроматичность на два измерения. Один из распространённых методов используется в цветовых пространствах HSL и HSV. В обоих цветовых пространствах хроматичность разделяется на «тон» (hue) и «насыщенность» (saturation):

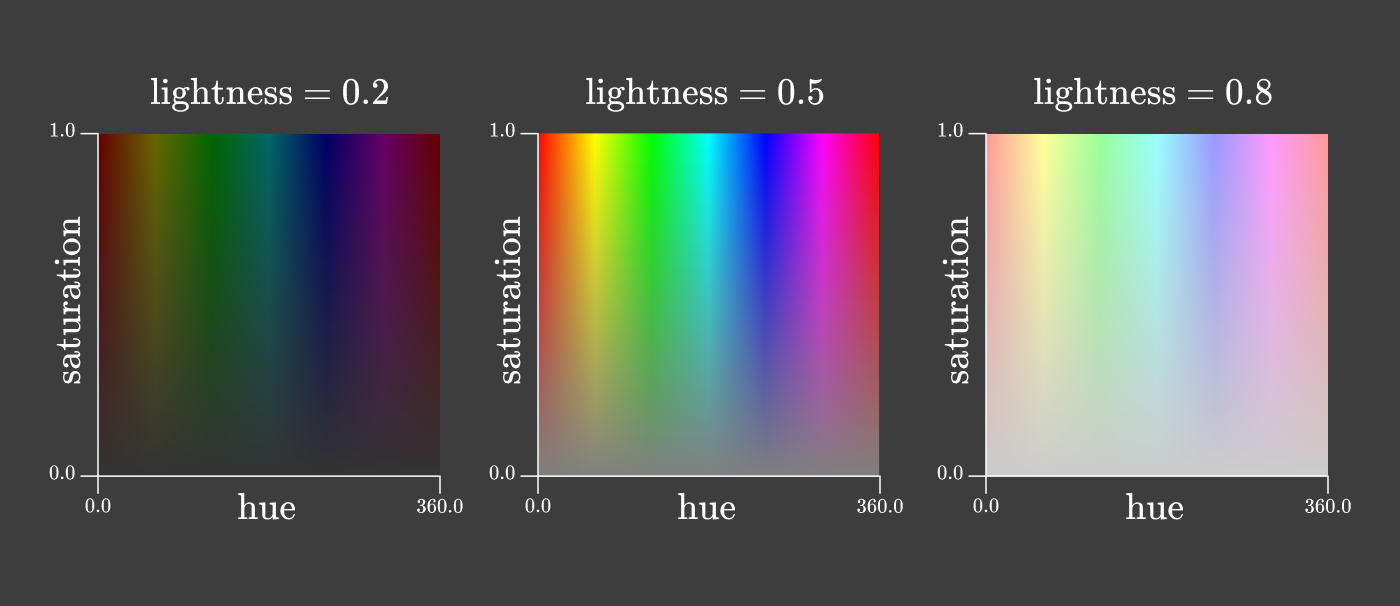
На первый взгляд может показаться, что треугольник rg-хроматичности и эти квадраты тона/насыщенности содержат все цвета радуги. Что ж, пришло время снова вернуться к тем надоедливым отрицательным значениям в функциях сложения цветов.

Гаммы и спектральный локус
Если взять наши функции сложения цветов $\bar r(\lambda)$ , $\bar g(\lambda)$ и $\bar b(\lambda)$ и построить rg-хроматичность спектральных цветов, то получится примерно такой график:

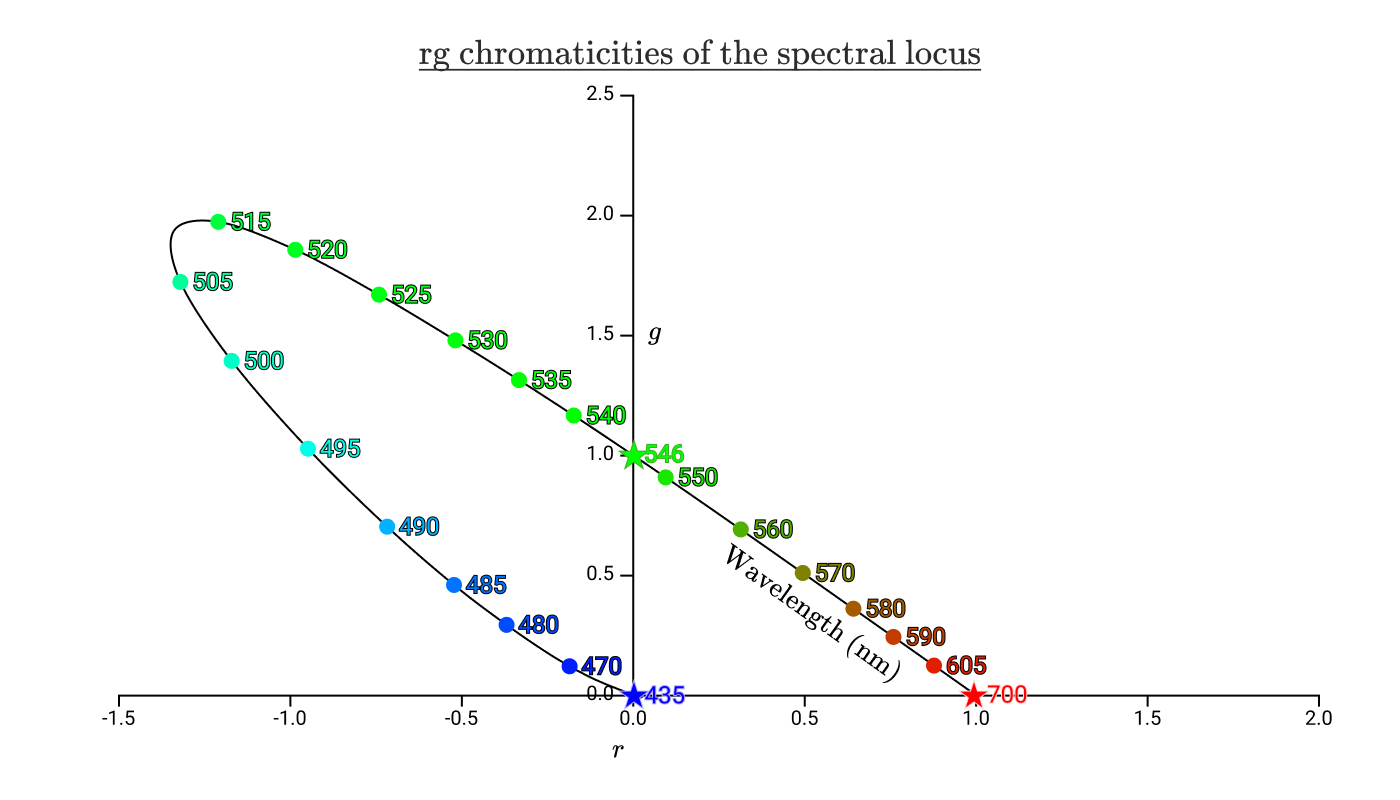
Чёрная кривая с цветными точками показывает хроматичность всех чистых спектральных цветов. Кривая называется спектральным локусом. Звёздочки соответствуют длинам волн в лампах, которые использовались в экспериментах по сложению цветов.

Наложим предыдущие треугольники хроматичности на эту диаграмму.

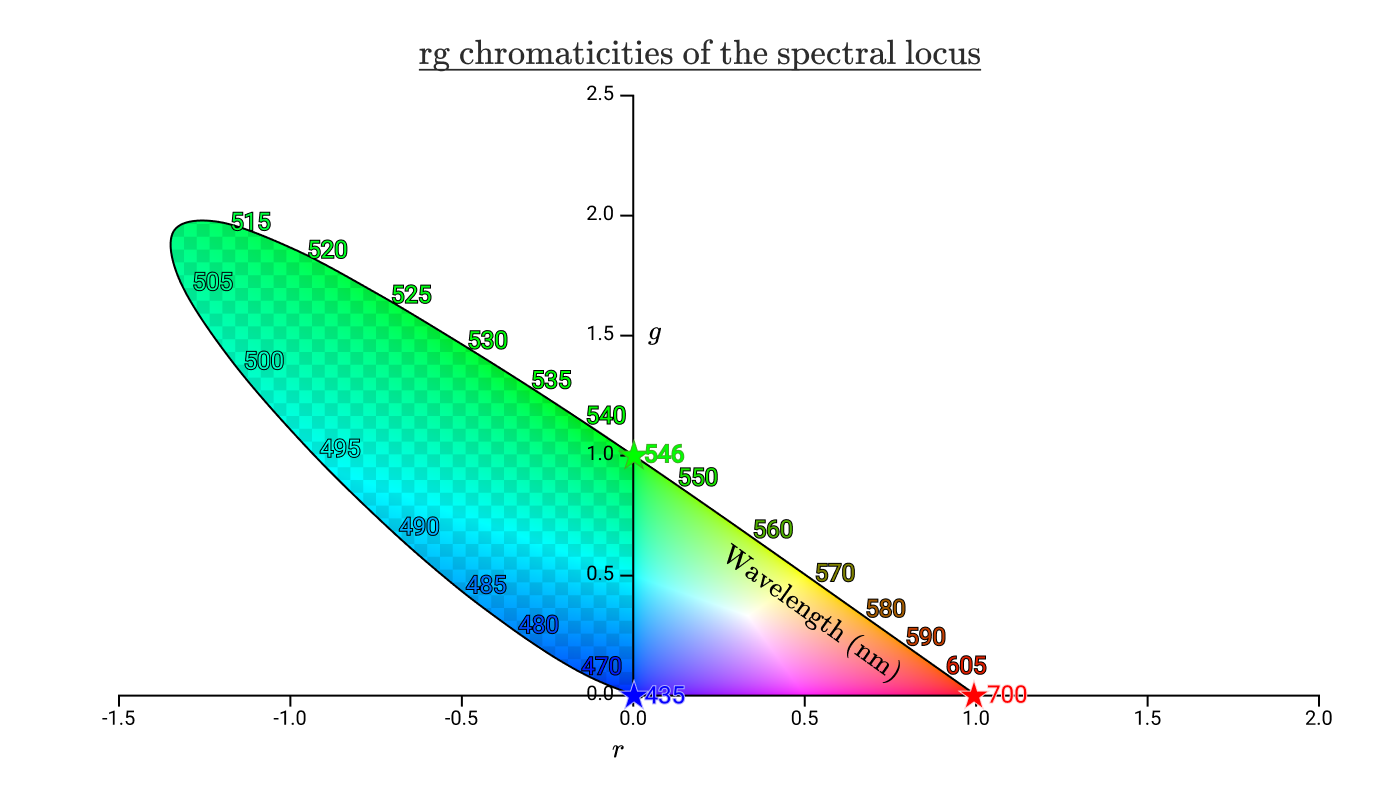
Область внутри спектрального локуса содержит все цвета, видимые человеком. Зона шашечек показывает цвета, которые человек воспринимает, но их невозможно воспроизвести сложением волн 435 нм, 546 нм и 700 нм. Из этой диаграммы видно, что мы не можем воспроизвести ни один из спектральных цветов между 435 нм и 546 нм, включая чистый циан.

Треугольник справа без шашечек — это все цвета, которые можно воспроизвести положительными значениями R, G, B. Мы называем эту область гаммой цветового пространства.

Прежде чем наконец-то вернуться к шестнадцатеричным кодам, нужно рассмотреть ещё одно цветовое пространство.

Цветовое пространство CIE XYZ
В 1931 году была созвана Международная комиссия по освещению. Она установила два цветовых пространства. Первое — цветовое пространство RGB, которое мы уже обсуждали, созданное на основе экспериментов Райта и Гилда по сложению цветов. Вторым стало цветовое пространство XYZ.

Одна из задач цветового пространства XYZ — получить положительные значения для всех цветов, видимых человеком, чтобы все значения хроматичности находились в диапазоне [0, 1] на обеих осях. Для этого тщательно подобрали подходящее линейное преобразование пространства RGB.

$\begin{bmatrix} X \\ Y \\ Z \end{bmatrix} = \frac{1}{b_{21}} \begin{bmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{bmatrix} \begin{bmatrix} R \\ G \\ B \end{bmatrix} = \frac{1}{0.17697} \begin{bmatrix} 0.49000 & 0.31000 & 0.20000 \\ 0.17697 & 0.81240 & 0.010630 \\ 0.0000 & 0.010000 & 0.99000 \end{bmatrix} \begin{bmatrix} R \\ G \\ B \end{bmatrix}$

Аналогом rg-хроматичности в пространстве XYZ является xy-хроматичность, а диаграммы хроматичности размещаются в более стандартной системе координат.

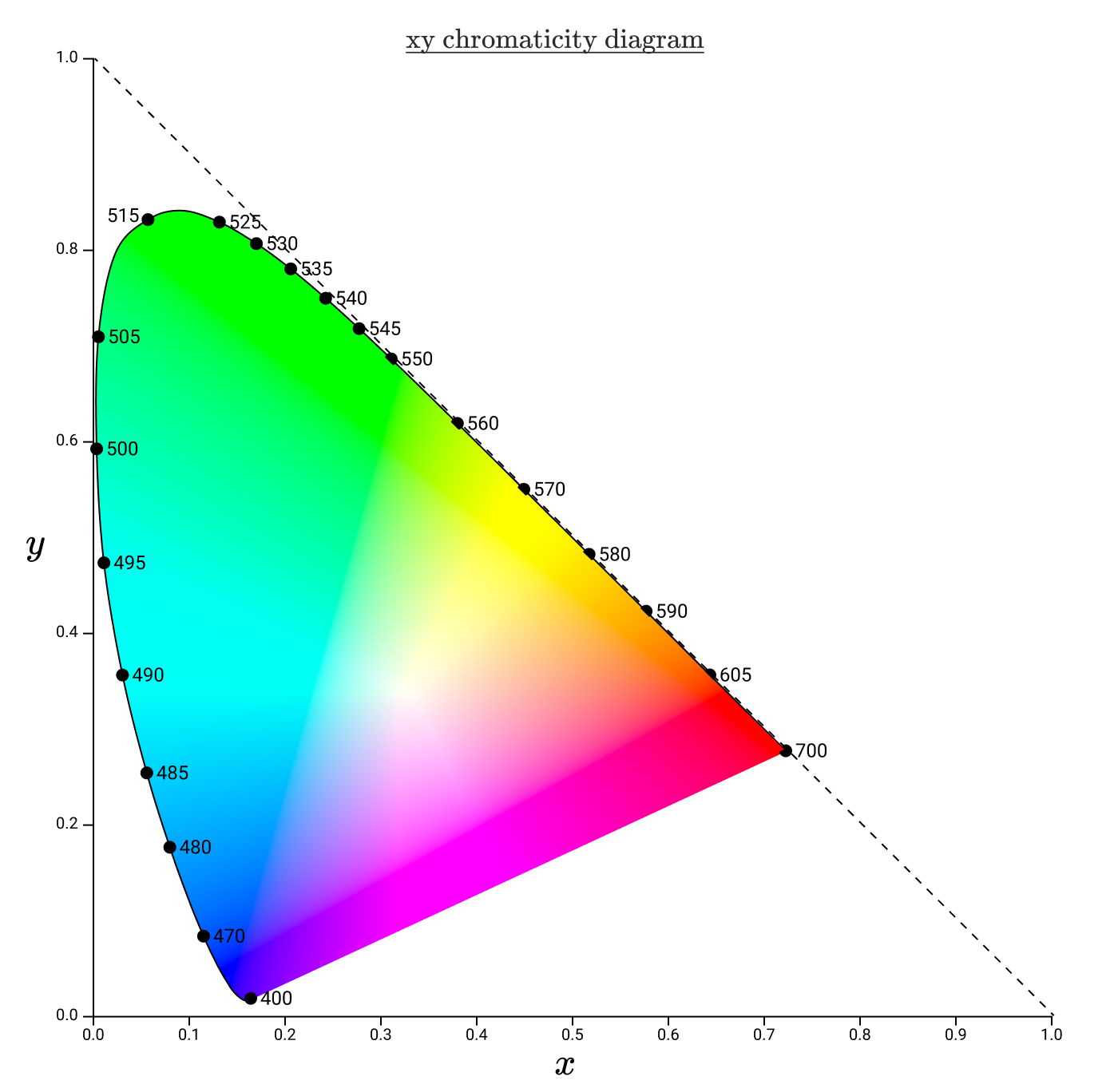
Гаммы обычно представляют треугольниками на диаграмме xy-хроматичности. Например, вот ещё раз гамма CIE RGB, на этот раз в пространстве xy.

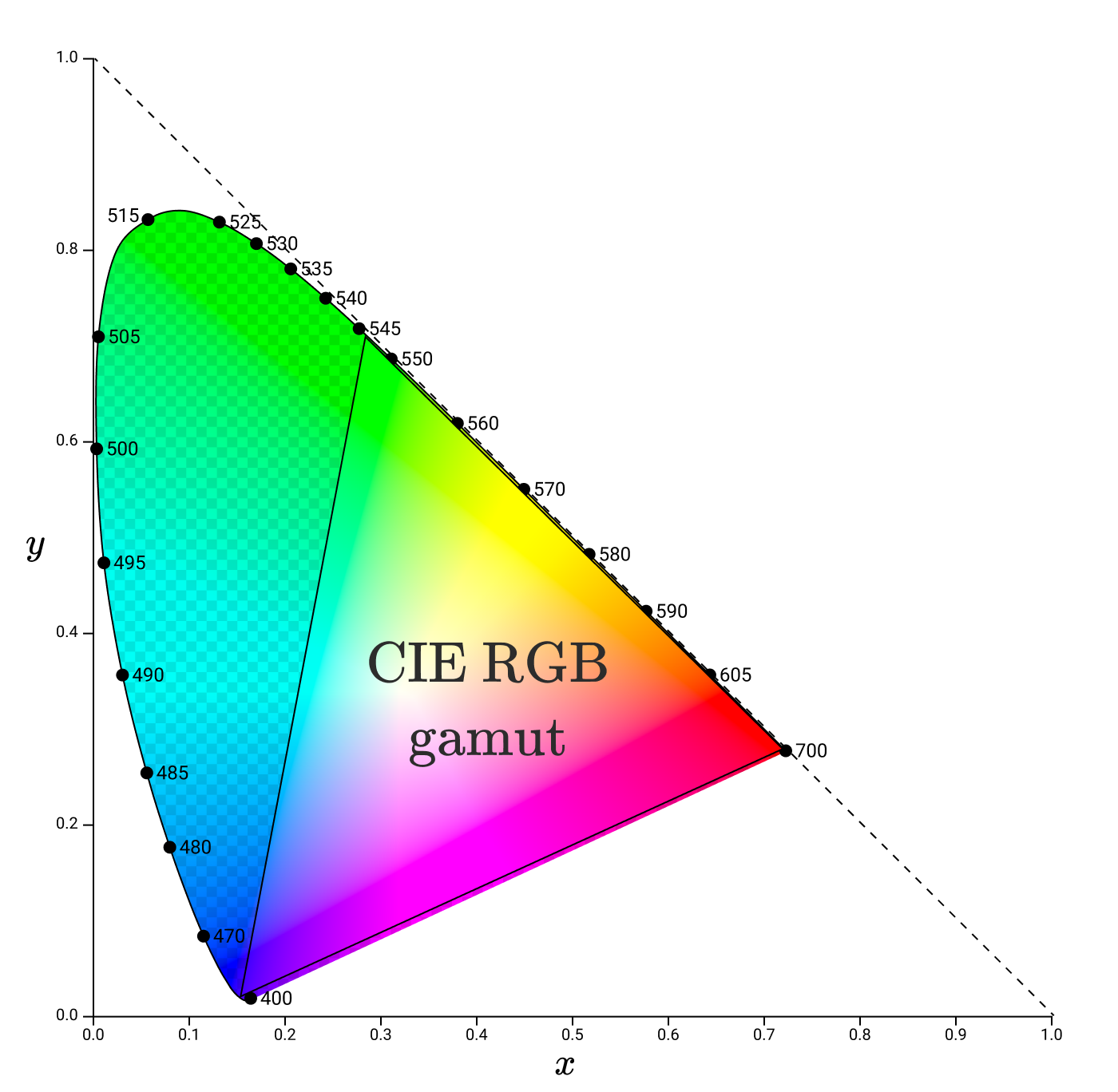
Поняв гаммы & хроматичность, мы наконец-то можем начать обсуждение, как цифровые дисплеи способны показывать нужные цвета.

Субпиксели экрана
Независимо от производителя дисплея под сильной лупой вы увидите сетку пикселей, где каждый пиксель состоит из трёх субпикселей: один красный, один зелёный и один синий. Она может выглядеть примерно так:

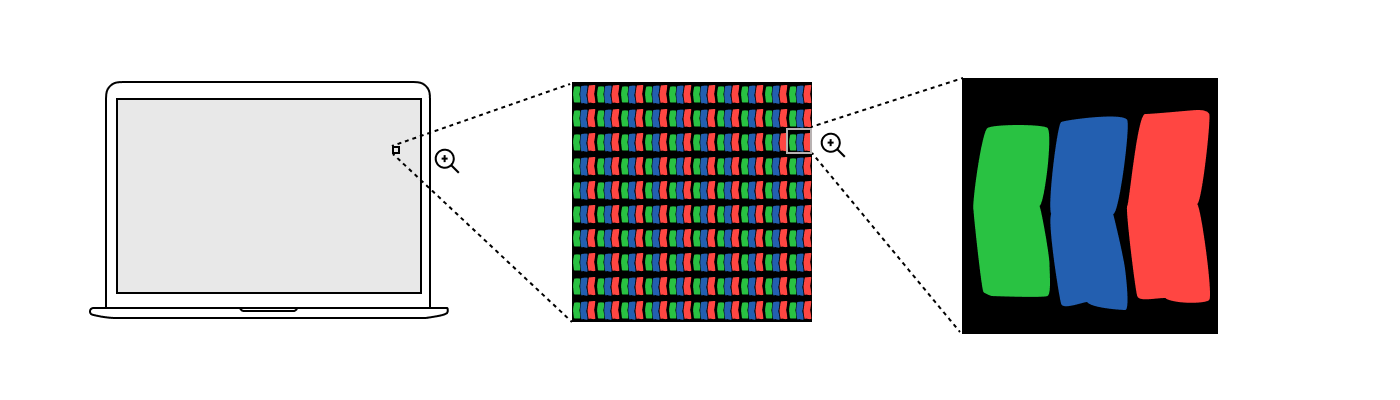
В отличие от ламп в эксперименте по сложению цветов, субпиксели не излучают монохроматический свет. У каждого типа субпикселей своё собственное спектральное распределение, разное у разных мониторов.

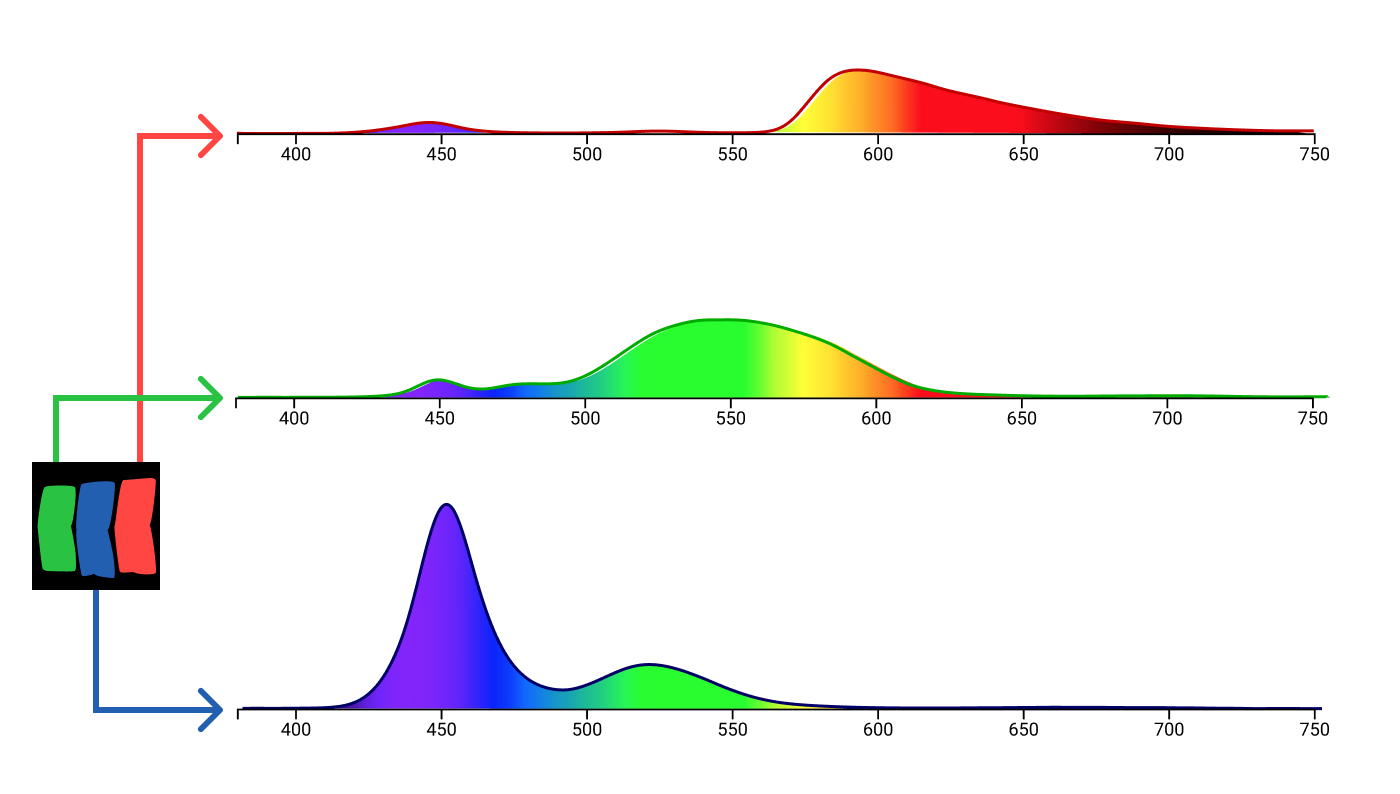
Субпиксельные спектральные данные MacBook Air из f.luxometer

С помощью утилиты ColorSync я определил гамму в xy пространстве для дисплея своего Macbook Pro.

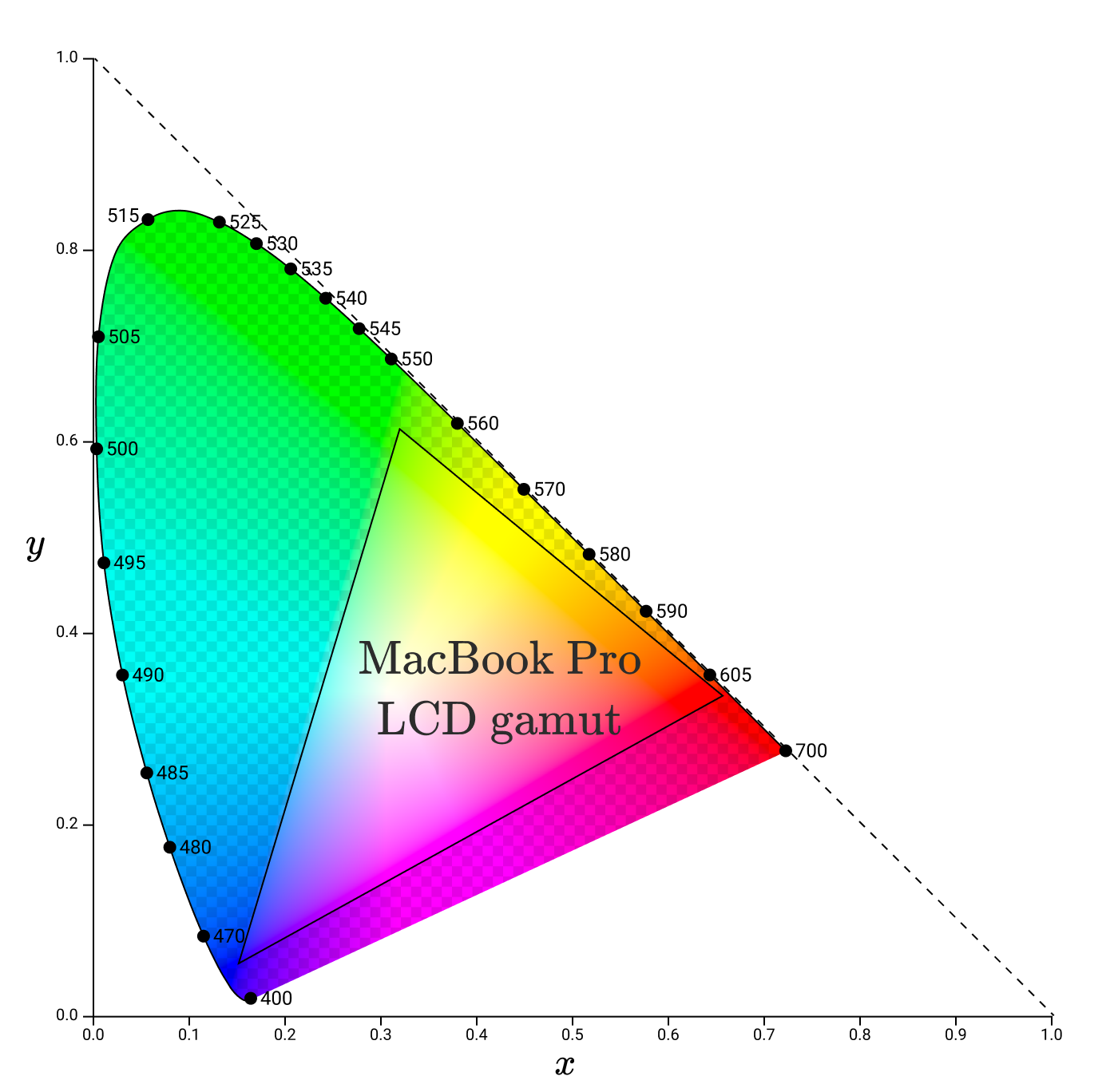
Обратите внимание, что углы гаммы больше не лежат вдоль спектрального локуса. Оно и понятно, ведь субпиксели не излучают чистый монохроматический свет. Эта гамма представляет полный спектр цветности основных цветов, которые данный монитор может точно воспроизвести.

В то время как гаммы мониторов будут различаться, современные мониторы должны попытаться охватить определённую другую гамму: sRGB.

sRGB
sRGB («стандартный красный зелёный синий») — это цветовое пространство, созданное HP и Microsoft в 1996 году для точной передачи информации о цвете между разными устройствами.

Стандарт определяет хроматичность основных цветов.

Хроматичность	Красный	Зелёный	Синий
x	0,6400	0,3000	0,1500
y	0,3300	0,6000	0,0600
Y	0,2126	0,751	0,0722

Если нанести их на цветовое пространство, то получится гамма, похожая на гамму ЖК-экрана MacBook, но чуть меньше.

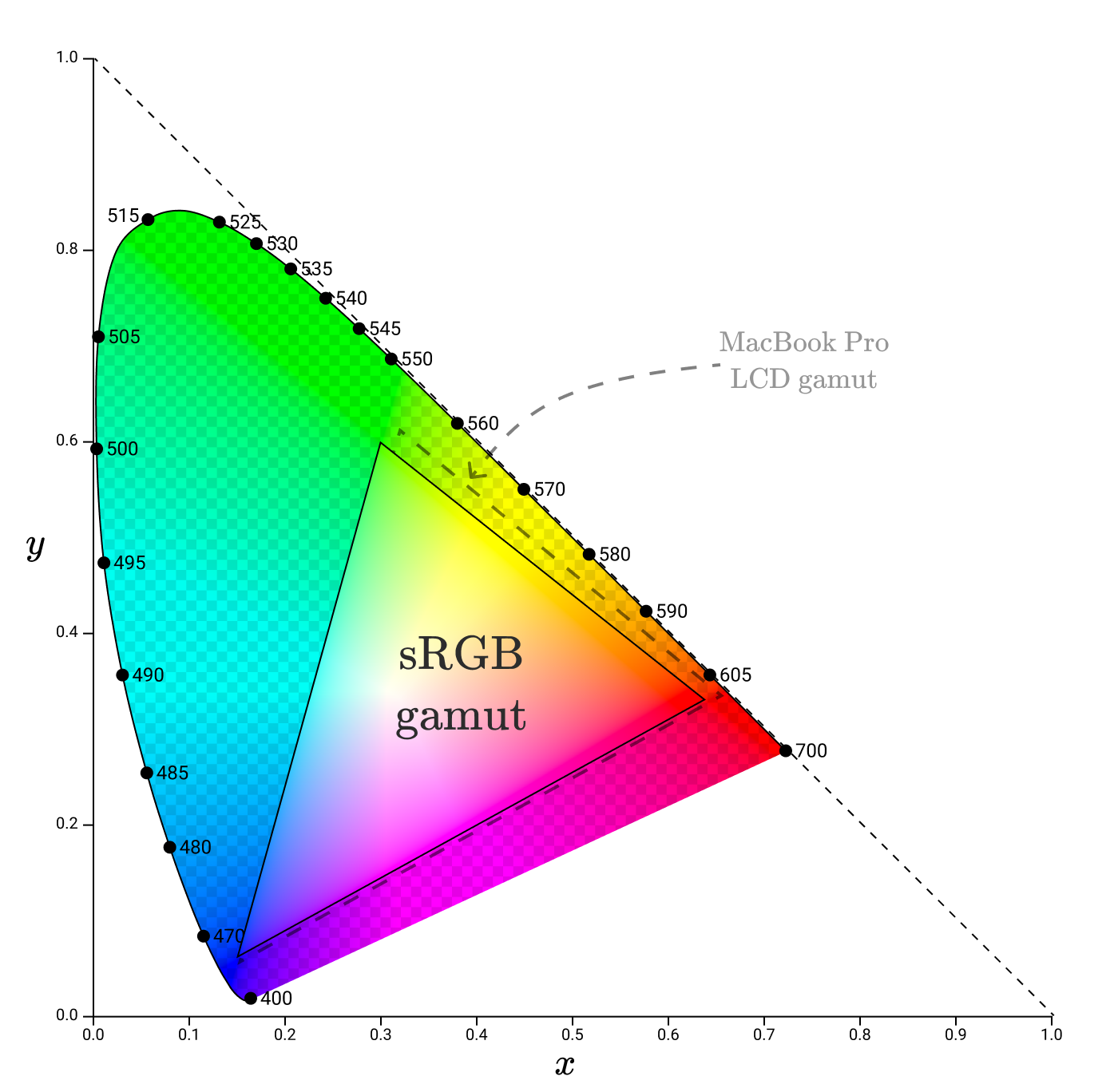
Некоторые части официальной гаммы sRGB не входят в гамму ЖК-дисплея MacBook Pro, то есть дисплей не может точно их воспроизвести. Для этого MacBook, похоже, использует модифицированную гамму sRGB.

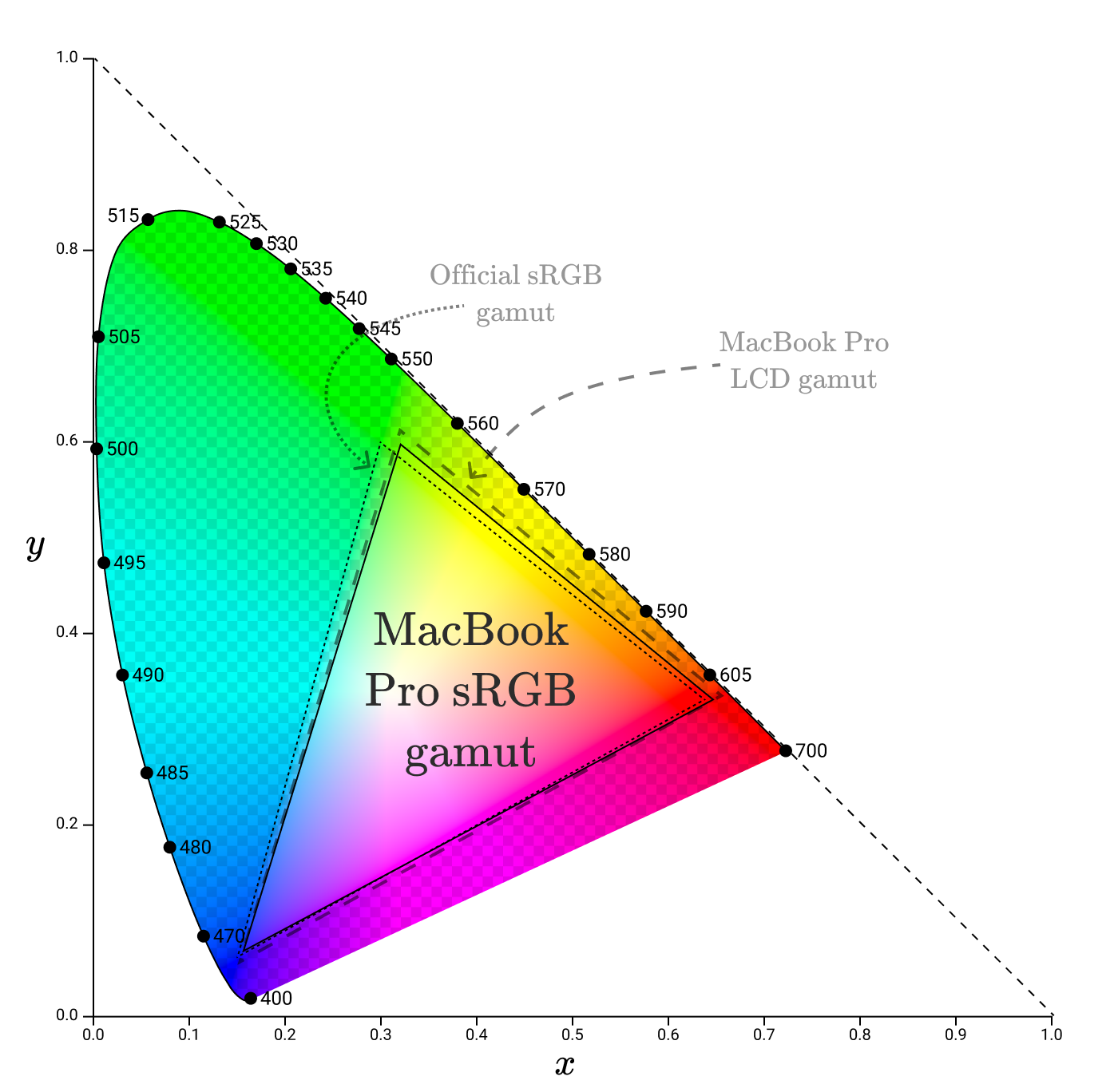
sRGB — цветовое пространство по умолчанию, которое используется почти везде. Это и стандартное цветовое пространство для браузеров (указанное в стандарте CSS). Все диаграммы в этой статье находятся в цветовом пространстве sRGB. Это значит, что все цвета за пределами гаммы sRGB неправильно воспроизводятся на диаграммах!

Что приводит нас, наконец, к кодам цветов в интернете.

Шестнадцатеричные коды sRGB
#9B51E0 задаёт цвет в пространстве sRGB. Чтобы преобразовать его в соответствующие координаты (R, G, B), мы делим каждую из трёх составляющих на 0xFF, то есть на 255. В данном случае:

0x9B / 0xFF = 0.61 0x51 / 0xFF = 0.32 0xE0 / 0xFF = 0.88

Поэтому цвету #9BE1E0 будут соответствовать координаты $(0.61, 0.32, 0.88)$ .

Прежде чем отправить эти значения на дисплей для установки интенсивности субпикселей, нужно выполнить ещё один шаг: гамма-коррекцию.

Гамма-коррекция
Если у каждой координаты в пространстве RGB есть 256 возможных значений, то хотелось бы убедиться, что каждая пара соседних координат максимально отличается друг от друга. Например, что #030000 отличался от #040000 как #F40000 от #F50000.

Человеческое зрение гораздо более чувствительно к небольшим изменениям слабого света, чем сильного света, поэтому желательно разместить больше из этих 256 значений в области слабого света.

Представим, что мы хотим закодировать оттенки серого, но у нас для этого есть только три бита, что даёт восемь возможных значений.

Если построить значения серого как линейную функцию энергии, то она будет выглядеть примерно так:

Назовём это трёхбитное значение $Y$ . Если все значения распределить равномерно ( $Y = \frac{\left\lfloor8E\right\rfloor}{8}$ ), то получится следующая картина:

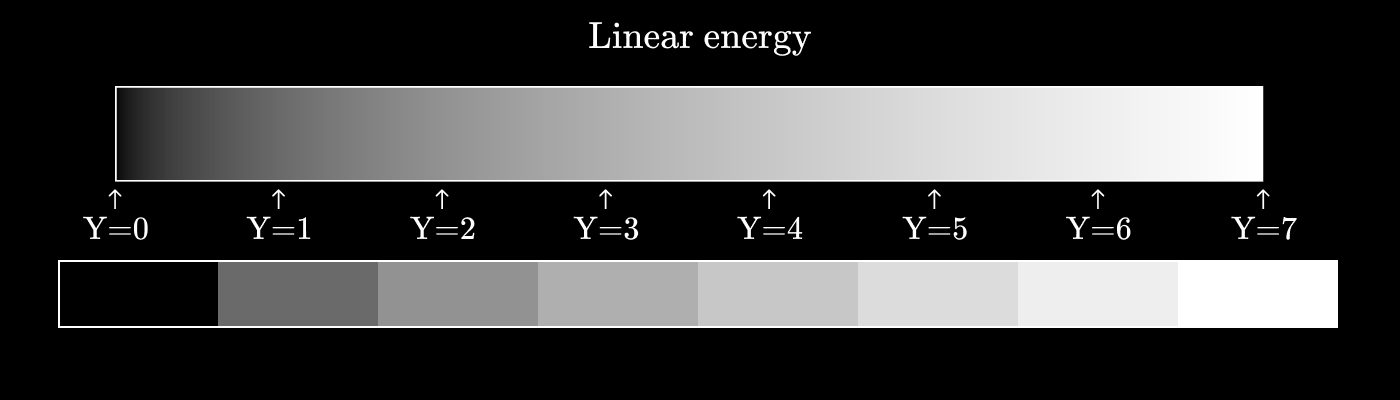
Как видите, разница в восприятии между $Y=0$ и $Y=1$ значительно больше, чем между $Y=6$ и $Y=7$ .

Теперь посмотрим, что произойдёт, если вместо этого использовать степенную функцию. Попробуем $Y = \left(\frac{\left\lfloor8E\right\rfloor}{8}\right)^2$

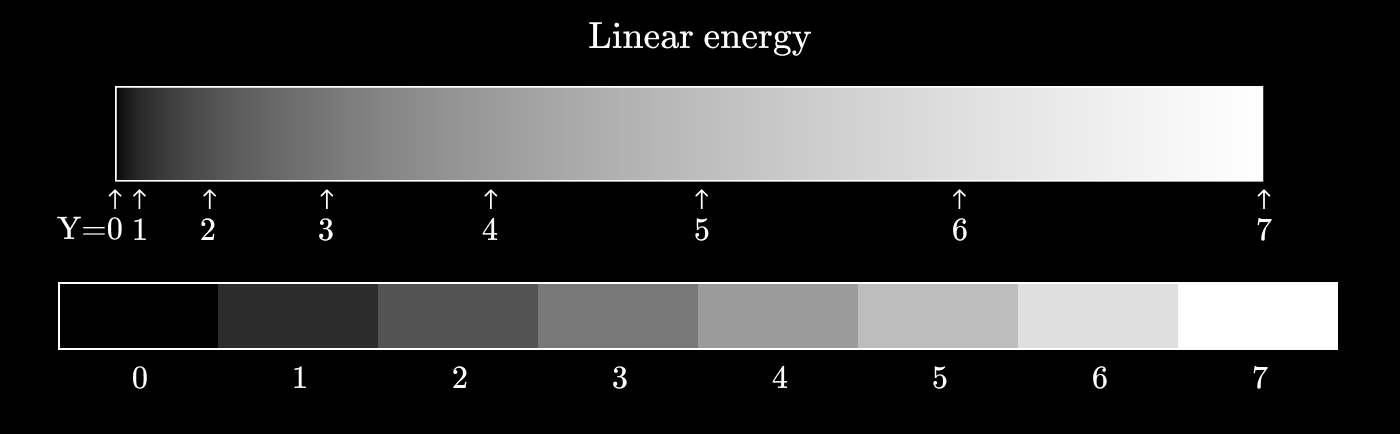
Мы стали гораздо ближе к единообразию восприятия, чтобы каждая соседняя пара значений отличалась в такой же степени, как и любая другая соседняя пара.

Такое преобразование значений энергии в дискретные значения называется гамма-кодирование. Обратная операция (преобразование дискретных значений в энергетические) называется гамма-декодированием.

В общем виде гамма-коррекция выполняется по формуле $V_{out} = A V_{in}^\gamma$ . Экспонента обозначается греческой буквой «гамма», отсюда и название.

Правила кодирования и декодирования для sRGB основаны на аналогичной идее, но формула немного сложнее.

$$C_\mathrm{linear}= \begin{cases}\frac{C_\mathrm{sRGB}}{12.92}, & C_\mathrm{sRGB}\le0.04045\\ \left(\frac{C_\mathrm{sRGB}+0.055}{1.055}\right)^{2.4}, & C_\mathrm{sRGB}>0.04045 \end{cases}$» /> Если построить значения sRGB относительно линейных значений, то получится такой график: <img src=$

Отлично! Это последний фрагмент паззла для понимания, как мы переходим от шестнадцатеричных кодов к восприятию глазом! Составим пошаговое руководство.

От шестнадцатеричных кодов до глаза
Во-первых, берем #9B51E0, разбиваем на компоненты R, G, B и нормализуем эти компоненты в диапазоне $[0, 1]$ .

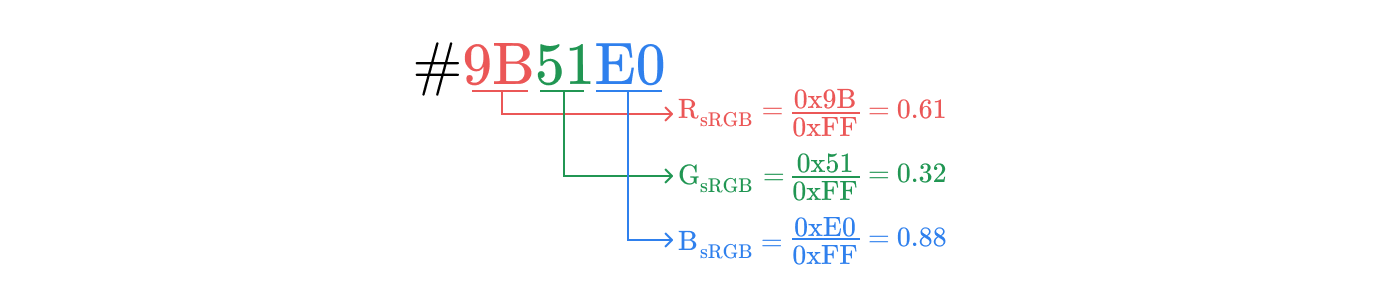
Это даёт нам координату $(0.61, 0.32, 0.88)$ в пространстве sRGB. Затем берём наши компоненты sRGB и преобразуем их в линейные значения.

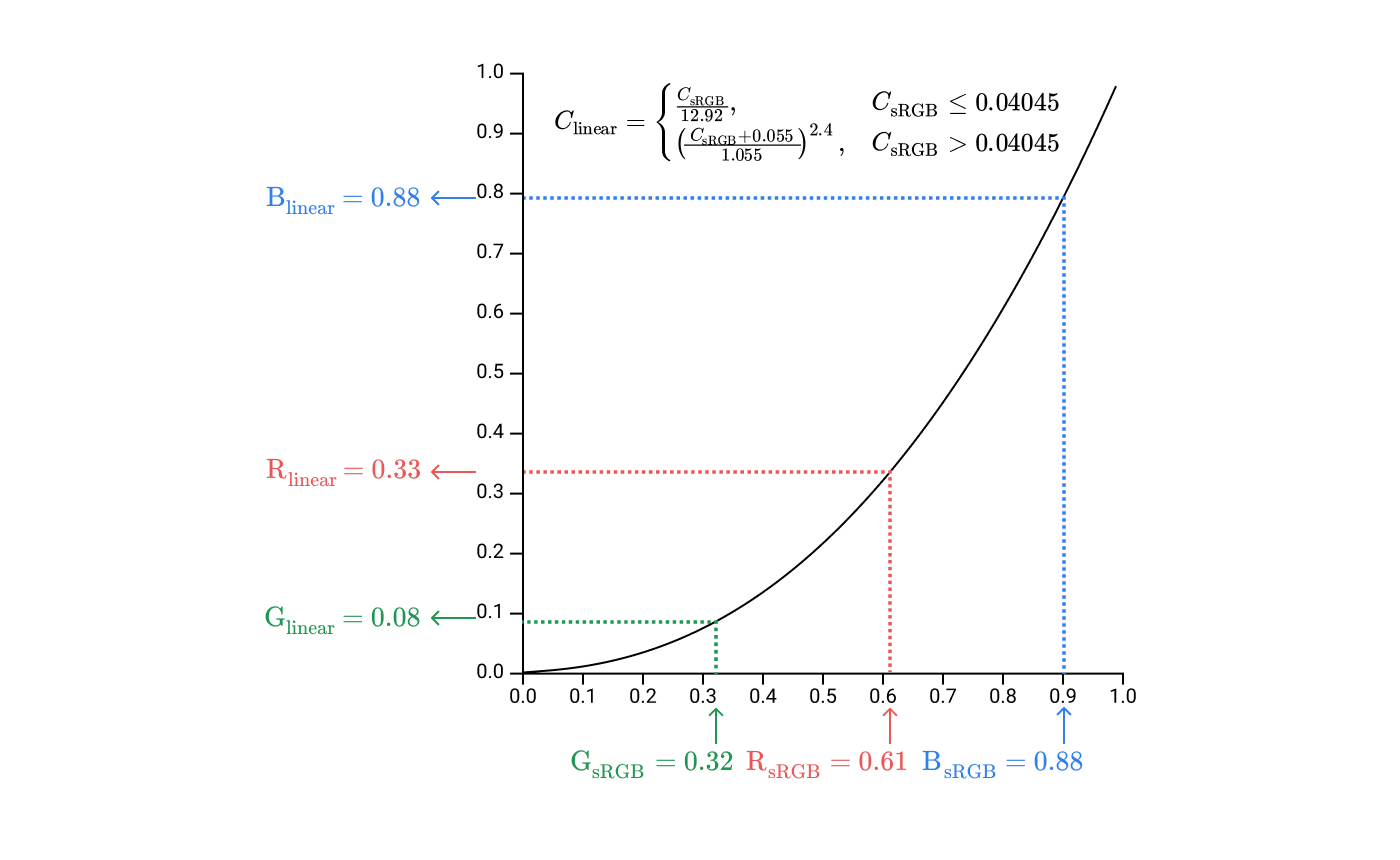
Это даёт нам координату $(0.33, 0.08, 0.10)$ в линейном пространстве RGB. Данные значения используются для установки яркости субпикселей на экране.

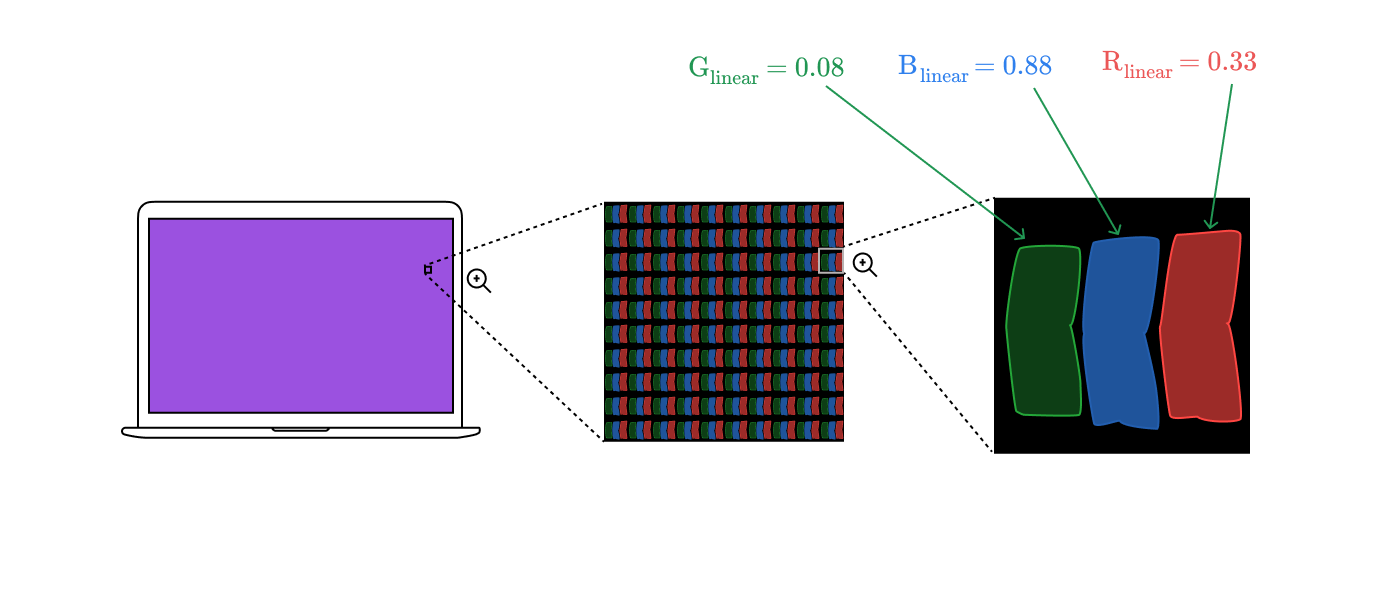
Спектральные распределения субпикселей объед